Robustness Against Deception in Unmanned Vehicle

Decision Making

William M. McEneaney

and Rajdeep Singh

Depts. of Mechanical/Aerospace Engineering and Mathematics

University of California at San Diego, La Jolla, CA 92093-0112, USA

Research partially supported by DARPA Contract NBCHC040168. and AFOSR Grant

FA9550-06-1-0238

Integrated Systems & Solutions, Information Assurance Group, Lockheed-Martin

La Jolla, CA, USA

Abstract. We are motivated by the tasking problem for UAVs in an adversarial

environment. In particular, we consider the problem where, in addition to purely

random noise in the observation process, the opponent may be applying decep-

tion as a means to cause us to make poor tasking choices. The standard approach

would be to apply the feedback-optimal controls for the fully-observed game, to

a maximum-likelihood state estimate. We ﬁnd that such an approach is highly

suboptimal. A second approach is through a concept taken from risk-sensitive

control. For the third approach, we formulate and solve the problem directly as

a partially-observed stochastic game. A chief problem with such a formulation

is that the information state for the player with imperfect information is a func-

tion over the space of probability distributions (a function over a simplex), and

so inﬁnite-dimensional. However, under certain conditions, we ﬁnd that the infor-

mation state is ﬁnite-dimensional. Computational tractability is greatly enhanced.

A simple example is considered, and the three approaches are compared. We ﬁnd

that the third approach is yields the best results (for such a case), although com-

putational complexity may lead to use of the second approach on larger problems.

1 Introduction

For a discrete deterministic game, one can apply dynamic programming techniques to

compute the value function (and “optimal” controls), deﬁned over the state space. For

discrete stochastic games, the value function is deﬁned over the space of all possible

probability distributions over the state space. Consequently, the problem is much more

computationally intensive. Finally, for discrete stochastic games with imperfect obser-

vations, the problem is yet more complex, and even simple games and their information

state formats become quite difﬁcult to analyze.

We will be concerned here with a speciﬁc class of discrete stochastic games under

imperfect observations. The choice of this class will be affected by both the intended

application and computational feasibility considerations. The motivational application

here is the military command and control (C

) problem for air operations, with un-

manned/uninhabited air vehicles (UAVs). See [2], [5], [16], [21], [28], [31], [24], [25]

M. McEneaney W. and Singh R. (2007).

Robustness Against Deception in Unmanned Vehicle Decision Making.

In Proceedings of the 3rd International Workshop on Multi-Agent Robotic Systems, pages 74-83

 SciTePress

for related information. This application has speciﬁc characteristics such that we will

be able to construct a reasonable problem formulation which is particularly nice from

the point of view of analysis and computation.

We ﬁrst outline the mathematical machinery. The details of the development are

discussed elsewhere due to paper length issues. After discussion of the algorithms, we

apply the techniques on a seemingly simple problem in order to determine their effec-

tiveness. We refer to the players in the game as Blue and Red, where the Blue player

has imperfect observations. We compare three Blue approaches on this simple game

problem. The most naive is for Blue to simply take the maximum likelihood estimate

of the Red state, and to apply a feedback control at this system state. As one can eas-

ily imagine, this approach is open to exploitation by Red deception. The second Blue

approach will apply a heuristic derived from the theory of Risk-Sensitive Control. This

technique is more cautious in its use of observational data. The third Blue approach (a

deception-robust approach) is through the direct solution of the imperfect information

stochastic game. As one would expect, there is an improvement in outcome with the

risk-sensitive and deception-robust approaches described herein when compared with

the standard maximum likelihood/certainty equivalence approach (although there is a

critical parameter in the risk-sensitive approach). On the other hand, there are signiﬁ-

cant computational requirements when using these new approaches.

2 Modeling the Game

We model the state dynamics as a discrete-time Markov chain. The state will take values

in a ﬁnite set, X . Time will be denoted by t ∈ {0, 1, 2, . . . , T }. We will consider only

the problem where there are exactly two players. Blue controls will take values in a

ﬁnite set, U, and Red controls will take values in a ﬁnite set, W . Given Blue and Red

controls, and a system state, there are probabilities of transitioning to other possible

states. We let P

i,j

(u, w) denote the probability of transitioning from state i to state j in

one time step given that the Blue and Red controls are u ∈ U and w ∈ W , respectively.

Also, P (u, w) will denote the matrix of such transition probabilities. We must allow for

feedback controls. That is, the control may be state-dependent. For technical reasons,

we will ﬁnd that we speciﬁcally need to consider Red feedback controls. Suppose the

size of X is n, i.e. that there are n possible states of the system. Then we may represent

a Red feedback control as w ∈ W

, an n-dimensional vector with components having

values in W . Speciﬁcally, w

= ¯w ∈ W implies that Red plays ¯w if the state is i.

Deﬁne matrix

P (u, w) by

i.j

(u, w) = P

i,j

(u, w

) ∀ i, j ∈ X . (1)

Let ξ

denote the (stochastic) system state at time t. Let q

be the vector of length n

whose i

component is the probability that the state is i at time t, that is the probability

that ξ

= i. Then if Blue plays u and Red plays w, the probability propagates as

t+1

′

(u, w)q

. (2)

We suppose there is a terminal cost for the game which is incurred at terminal time,

T . Let the cost for being in terminal state ξ

= i ∈ X be E(i), which we will also

sometimes ﬁnd convenient to represent as the i

component of a vector, E (where we

note the abuse of notation due to use of E for two different objects). Suppose that at time

T − 1, the state is ξ

T −1

= i

, and that Blue plays u

T −1

∈ U and Red plays w ∈ W

Then, the expected cost would be E[E(ξ

)] = q

′

E where q

′

(u, w)q

T −1

with

T −1

being 1 at i

and zero in all other components.

We also need to deﬁne the observation process. We suppose that Red has perfect

state knowledge, but that Blue obtains its state information through observations. Let

the observations take values y ∈ Y . We will suppose that this observation process can

be inﬂuenced not only by random noise, but also by the actions of both players. For

instance, again in a military example, Blue may choose where to send sensing entities,

and Red may choose to have some entities act stealthily while having some other en-

tities exaggerate their visibility, for the purposes of deception. We let R

(y, u, w) be

the probability that Blue observes y given that the state is i and Blue and Red employ

controls u and w. We will also ﬁnd it convenient to think of this as a vector indexed by

i ∈ X .

We suppose that at each time, t ∈ {0, 1, . . . T − 1}, ﬁrst an observation occurs, and

then the dynamics occur. We let q

be the a priori distribution at time t, and bq

be the a

posteriori distribution. With this, the dynamics update of (2) is rewritten as

t+1

′

, w

)bq

(3)

with controls u

, w

at time t. The observation, say y

= y, at time t updates q

to bq

via Bayes rule,

[bq

]

P (y

= y |ξ

= i, u, w)[q

]

k∈X

P (y

= y |ξ

= k, u, w)[q

]

. (4)

Then (3), (4) deﬁne the dynamics of the conditional probabilities.

2.1 Risk-Averse Controller Theory

In linear control systems with quadratic cost criteria, the control obtained through the

separation principle is optimal. That is, the optimal control is obtained from the state-

feedback control applied at the state given by

x = argmax

(i)] .

A different principle, the certainty equivalence principle, is appropriate in robust con-

trol. We have applied a generalization of the controller that would emanate from this

latter principle. This generalization allows us to tune the relative importance between

the likelihood of possible states and the risk of misestimation of the state. Let us moti-

vate the proposed approach in a little more detail.

In deterministic games under partial information, the certainty equivalence principle

indicates that one should use the state-feedback optimal control corresponding to state

x = argmax [I

(x) + V

(x)] (5)

where I is the information state and V is the value function [13] (assuming uniqueness

of the argmax of course). In this problem class, the information state is essentially the

worst case cost-so-far, and the value is the minimax cost-to-come. So, heuristically, this

is roughly equivalent to taking the worst-case possibility for total cost from initial time

to terminal time. (See, for instance, [20], [17], [22], [29], [30].)

The deterministic information state is very similar to the log of the observation-

conditioned probability density in stochastic formulations for terminal/exit cost prob-

lems. In fact, this is exactly true for a class of linear/quadratic problems. In such prob-

lems, the I

term in (5) is replaced by the log of the probability density, and a risk-

sensitivity coefﬁcient appears as well. Although we are outside of that problem class

here, we nonetheless apply the same approach, but where now the correct value of this

risk-sensitivity parameter is not as obvious. In particular, the risk-sensitive algorithm is

as follows: Apply state-feedback control at

∗

= argmax

{log[bq

(i)] + κV

(i)} (6)

where bq is the probability distribution based on the conditional distribution for Blue

given by (3), (4) and a stochastic model of Red control actions, and V is state-feedback

stochastic game value function (c.f. [13]). Here, κ ∈ [0, ∞) is a measure of risk aver-

sion. Note that κ = 0 implies that one is employing a maximum likelihood estimate in

the state- feedback control (for the game), i.e. argmax

{log([bq

]

)} = argmax

{[bq

]

Note also (at least in linear-quadratic case where log[bq

]

= I

(i) modulo a constant),

κ = 1 corresponds to the deterministic game certainty equivalence principle [17], [20],

i.e. argmax{I

(i) + V

(i)}. As κ → ∞, this converges to an approach which always

assumes the worst possible state for the system when choosing a control – regardless of

observations. (See [28] for further discussion.)

2.2 Deception-Robust Controller Theory

The above approach was cautious (risk averse) when choosing the state estimate at

which to apply state-feedback control. We now consider a controller which explicitly

reasons about deception. This approach typically handles deception better that the risk-

averse approach, but this improvement comes at a substantial computational cost. For

a given, ﬁxed computational limit, depending on the speciﬁc problem, it is not obvious

which approach will be more successful.

Here we ﬁnd that the truly proper information state for Red is I

: Q(X ) → R,

where Q(X ) is the space of probability distributions over state space X ; Q(X ) is the

simplex in ℜ

such that all components are non-negative and such that the sum of

the components is one. We let the initial information state be I

(·) = φ(·). Here, φ

represents the initial cost to obtain and/or obfuscate initial state information. The case

where this information cannot be affected by the players may be represented by a max-

plus delta function. The information state at time t evaluated at probability distribution

q, I

(q), essentially represents the cost to the opponent to generate distribution q as

the naive/Bayesian distribution in a Blue estimator. That is, through obfuscation of the

initial intelligence and use of controls w

up to time t, the propagation (3), (4) would

lead to some q at time t if such w

were known. I

(q) would be the maximal (worst

from Blue perspective) cost to generate q by any Red controls that would yield that

particular q at time t. Although Blue does not know the Red controls, it can nonetheless

compute I

(·). For details on this propagation and theory, see [26].

In the case here, where the state-space is ﬁnite of size n = #X , Q is some a simplex

in IR

. Thus, I

belongs to a space of functions over an n − 1 dimensional simplex, and

consequently an element of an inﬁnite-dimensional space. However, in the cases where

φ is either a max-plus delta function, or a piecewise-continuous function, I

is ﬁnite

dimensional. This is crucial to the computability of this controller. Note that in either

of these cases, the complexity of I

is proportional (in the worse case) to (#W )

at the

t time-step. Pruning strategies for reduction of this complexity are critical (c.f., [23]).

We now turn to the second component of the theory, computation of the state-

feedback value function. In this context, our value function is a generalized value func-

tion in that it is a function not only of the physical state of the system, but also of what

probability distribution Blue believes reﬂects its lack of knowledge of this true physical

state. The full, generalized state of the system is now described by the true state taking

values x ∈ X and the Blue conditional probability process taking values q ∈ Q(X ).

We denote the terminal cost for the game as E : X → R (where of course this does not

depend on the internal conditional probability process of Blue). Thus the state-feedback

value function at the terminal time is

(x, q) = E(x). (7)

The value function at any time, t < T , takes the form V

(x, q). It is he above minimax

expected payoff where Blue assumes that q is the “correct” distribution for x at time

t, that at each time Blue will know the correct q, and that Red will know both the

true physical state and this distribution, q. In particular, q will propagate according to

(2), and the state will propagate stochastically, governed by (1). Loosely speaking, this

generalized value function is the minimax expected payoff if Blue believes the state to

be distributed by q

at each time r ∈ (t, T ], while Red knows the true state (as well as

). A rigorous mathematical deﬁnition can be found in [26]. The backward dynamic

program that compute V

from V

t+1

is as follows.

1. First, let the vector-valued function M

be given component-wise by

]

(q, u) = max

w∈W

j∈X

(u, w)V

t+1

(j, q

′

(q, u, w))

(8)

where q

′

(q, u, w) =

(u, w) and the optimal w is

= w

(x, q, u) = argmax

w∈W

j∈X

(u, w)V

t+1

(j, q

′

(q, u, w))

2. Then deﬁne L

(q, u) = q

′

(q, u), (9)

and note that the optimal u is u

(q) = argmin

u∈U

(q, u).

(10)

3. With this, one obtains the next iterate from

(x, q) =

j∈X

, w

t+1

(j, q

′

(q, u

, w

)) = [M

]

(q, u

)

and the best achievable expected result from the Blue perspective is

(q) = q

′

(q, u

). (11)

Consequently, for each t ∈ {0, 1, . . . , T } and each x ∈ X , V

(x, ·) is a piecewise

constant function over simplex Q(X ). Due to this piecewise constant nature, propa-

gation is relatively straight-forward (more speciﬁcally, it is ﬁnite-dimensional in con-

tradistinction to the general case).

The remaining component of the computation of the control is now discussed. This

is typically performed via the use of the certainty equivalence principle (cf. [1], [17]),

and we employ the principle here as well. To simplify notation, note that by (9) and (8),

for any u,

(q, u) = E



max

w∈W

j∈X

(u, w)V

t+1

(j, q

′

(q, u, w))



Let us hypothesize that the optimal control for Blue is

= argmin

u∈U



max

q ∈Q(X )

(q) + L

(q, u)}



. (12)

In order to obtain the robustness/certainty Equivalence result below, it is sufﬁcient

to make the following Saddle Point Assumption. We assume that for all t,

sup

∈Q

min

u∈U

) + L

, u)

= min

u∈U

sup

∈Q

) + L

, u)

. (A-SP)

This type of assumption is typical in game theory. Although it is difﬁcult to verify for a

given problem, the alternative is a theory that cannot be translated into a useful result.

Finally, after some work [26], one obtains the robustness result:

Theorem 1. Let

t ∈ {0, T − 1}. Let I

, u

[0,

t−1]

and y

[0,

t−1]

be given. Let the Blue

control choice, u

, given by (12) be a strict minimizer. Suppose Saddle Point Assump-

tion (A-SP) holds. Then, given any Blue strategy, λ

[

t,T −1]

such that λ

] 6= u

, there

exists ε > 0, q

and w

[

t,T −1]

such that

sup

q ∈Q

(q) + L

(q, u

)} = Z

≤ I

) + E

X∼q

E[E(X

) | X

= X]

− ε

where X

denotes the process propagated with control strategies λ

[

t,T −1]

and w

[

t,T −1]

3 A Seemingly Simple Game

We now apply the above technology to an example problem in Command and Control

for UCAVs. This game will seem to be quite simple at ﬁrst. However, once one intro-

duces the partial information and deception components, determination of the best (or

even nearly best) strategy becomes quite far from obvious.

−60 −40 −20 0 20 40 60

100

110

Nonlinear Example − Only one Red required to take asset

Blue base

Blue asset

Roads are in green.

Red base

number decoys on

in right group

number decoys on

in left group

number units observed

on rightnumber units observed

on left

∆

Fig.1. Snapshot of Gameboard.

In this game the Red player has four ground entities (say, tanks) and the Blue player

has two UCAVs. The objective of Red player is to capture the high-value Blue assets

by moving at least one non-decoy Red entity to a Blue asset location by the terminal

time, T . Red can use stealth and decoys to obscure the direction from which the attack

will occur, while the Blue player uses the UCAVs to destroy the moving Red entities.

Red entities do not have any attrition capability against the Blue UCAVs. Blue UCAVs

require at least two time steps to travel from one route to the other.

The simulation snapshot in Figure 1, is taken after time step 2, from the graphic for a

MATLAB simulation that runs the example game. Red is moving its currently surviving

three entities (depicted as triangles) downward, while Blue is attempting to prevent any

Red entities from reaching the Blue asset through use of its UCAVs (depicted as blue

T’s). Red is currently employing a decoy on the right, while using stealth on the left.

Winning and losing are measured in terms of the total cost at the terminal time. The

cost at terminal time is computed as follows: each Red surviving entitiy costs Blue 1

point and if Blue loses the high-value asset, it costs Blue 20 points.

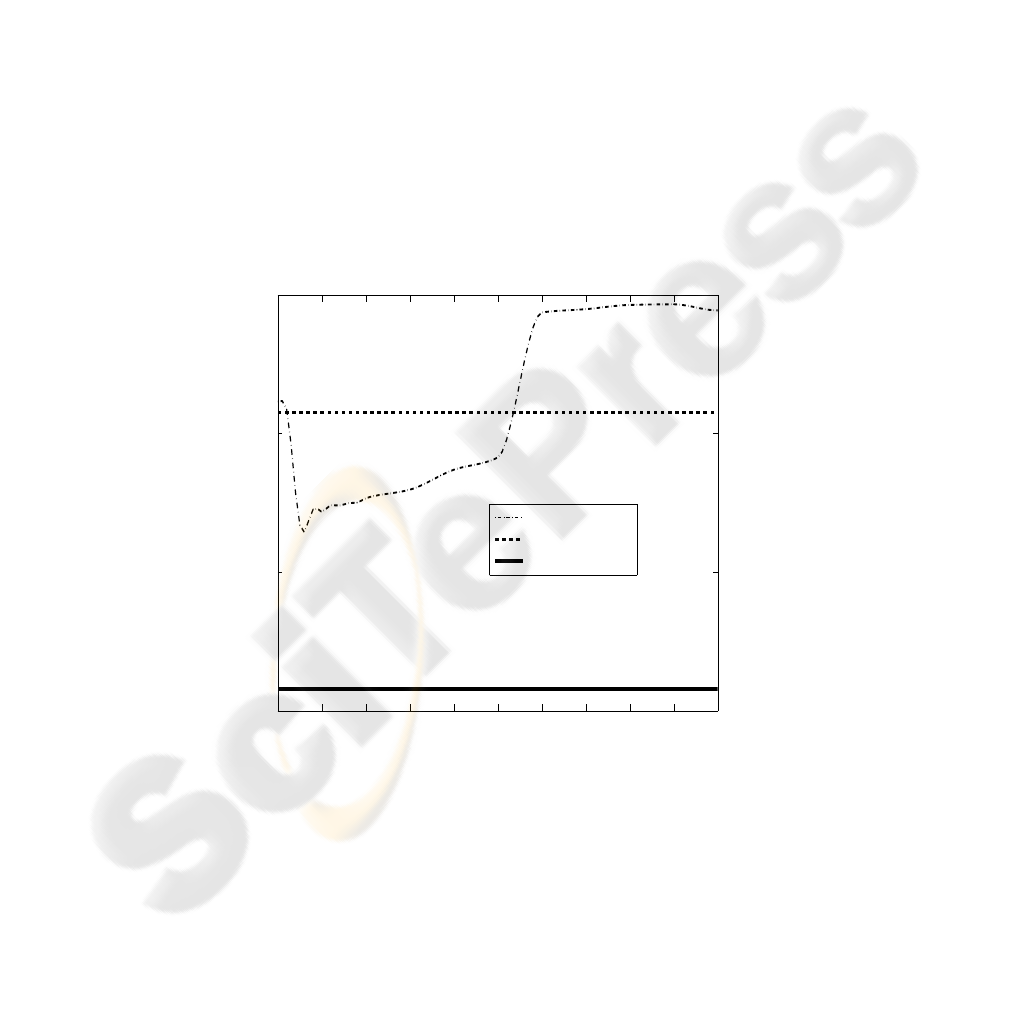
4 Comparison of the Approaches

Let us brieﬂy foray into a comparative study between the naive approach (i.e., feed-

back on maximum-likelihood state), the risk-averse algorithm and the deception-robust

approach for Blue. The critical component of the risk-averse approach is the choice of

the risk level, κ. For the example studied in this chapter we vary κ between 0 and 10

to demonstrate the nature of the risk-averse approach in general. Firstly, for the case

κ = 0, we have the risk-averse approach equivalent to the naive approach; apply the

state-feedback control at the MLS estimate. As κ increases we expect the approach to

achieve a lower cost for Blue, since it is taking into account the expected future cost

V (X

) (as a risk-sensitive measure). Note however that in the adversarial environment

the effect of the Red player’s control on the Blue player’s observations has more com-

plex consequences than that of random noise. As shown in the Figure 2, the risk-averse

approach gets the best cost for Blue at κ between 0.5 and 0.6 (note again that this choice

will be problem speciﬁc). As κ increases beyond this point, the expected cost begins in-

creasing, and has a horizontal asymptote which corresponds to a Blue controller which

ignores all the observations and assumes the worst-case possible Red conﬁguration.

0 1 2 3 4 5 6 7 8 9 10

kappa

Value

Risk−Averse

Maximum Likelihood State

Deception−robust

Comparing Different Blue Approach

Fig.2. Comparison of Approaches.

The bumpiness in the results is due to the sampling error (8000 Monte Carlo runs

were used for each data point in the plot.) Also note that for large κ, the risk-averse

approach does worse than the naive approach. For this speciﬁc example, the risk-averse

approach does not achieve the same low cost as achieved by using the deception-robust

approach.

References

1. T. Basar and P. Bernhard, H

∞

–Optimal Control and Related Minimax Design Problems,

Birkh

auser (1991).

2. D.P. Bertsekas, D.A. Casta

non, M. Curry and D. Logan, “Adaptive Multi-platform Schedul-

ing in a Risky Environment”, Advances in Enterprise Control Symp. Proc., (1999), DARPA–

ISO, 121–128.

3. P. Bernhard, A.-L. Colomb, G.P. Papavassilopoulos, “Rabbit and Hunter Game: Two Discrete

Stochastic Formulations”, Comput. Math. Applic., Vol. 13 (1987), 205–225.

4. T. Basar and G.J. Olsder, Dynamic Noncooperative Game Theory, Classics in Applied Math-

ematics Series, SIAM (1999), Originally pub. Academic Press (1982).

5. J.B. Cruz, M.A. Simaan, et al., “Modeling and Control of Military Operations Against Ad-

versarial Control”, Proc. 39th IEEE CDC, Sydney (2000), 2581–2586.

6. R.J. Elliott and N.J. Kalton, “The existence of value in differential games”, Memoirs of the

Amer. Math. Society, 126 (1972).

7. W.H. Fleming, “Deterministic nonlinear ﬁltering”, Annali Scuola Normale Superiore Pisa,

Cl. Scienze Fisiche e Matematiche, Ser. IV, 25 (1997), 435–454.

8. W.H. Fleming, “The convergence problem for differential games II”, Contributions to the

Theory of Games, 5, Princeton Univ. Press (1964).

9. W.H. Fleming and W.M. McEneaney, “Robust limits of risk sensitive nonlinear ﬁlters”, Math.

Control, Signals and Systems 14 (2001), 109–142.

10. W.H. Fleming and W.M. McEneaney, “Risk sensitive control on an inﬁnite time horizon”,

SIAM J. Control and Optim., Vol. 33, No. 6 (1995) 1881–1915.

11. W.H. Fleming and W.M. McEneaney, “Risk–sensitive control with ergodic cost criteria”,

Proceedings 31

IEEE Conf. on Dec. and Control, (1992).

12. W.H. Fleming and W. M. McEneaney, “Risk–sensitive optimal control and differential

games”, (Proceedings of the Stochastic Theory and Adaptive Controls Workshop) Springer

Lecture Notes in Control and Information Sciences 184, Springer–Verlag (1992).

13. W.H. Fleming and H.M. Soner, Controlled Markov Processes and Viscosity Solutions,

Springer-Verlag, New York, 1992.

14. W.H. Fleming and P.E. Souganidis, “On the existence of value functions of two–player, zero–

sum stochastic differential games”, Indiana Univ. Math. Journal, 38 (1989), 293–314.

15. A. Friedman, Differential Games, Wiley, New York, 1971.

16. D. Ghose, M. Krichman, J.L. Speyer and J.S. Shamma, “Game Theoretic Campaign Model-

ing and Analysis”, Proc. 39th IEEE CDC, Sydney (2000), 2556–2561.

17. J.W. Helton and M.R. James, Extending H

∞

Control to Nonlinear Systems: Control of Non-

linear Systems to Achieve Performance Objectives, SIAM 1999.

18. D.H. Jacobson, “Optimal stochastic linear systems with exponential criteria and their relation

to deterministic differential games”, IEEE Trans. Automat. Control, 18 (1973), 124–131.

19. M.R. James, “Asymptotic analysis of non–linear stochastic risk–sensitive control and differ-

ential games”, Math. Control Signals Systems, 5 (1992), pp. 401–417.

20. M. R. James and J. S. Baras, “Partially observed differential games, inﬁnite dimensional HJI

equations, and nonlinear H

∞

control”, SIAM J. Control and Optim., 34 (1996), 1342–1364.

21. J. Jelinek and D. Godbole, “Model Predictive Control of Military Operations”, Proc. 39th

IEEE CDC, Sydney (2000), 2562–2567.

22. M.R. James and S. Yuliar, “A nonlinear partially observed differential game with a ﬁnite-

dimensional information state”, Systems and Control Letters, 26, (1995), 137–145.

23. W.M. McEneaney and R. Singh, “Robustness against deception”, Adversarial Reasoning:

Computational Approaches to Reading the Opponent’s Mind, Chapman and Hall/CRC, New

York (2007), 167–208.

24. W.M. McEneaney and R. Singh, “Deception in Autonomous Vehicle Decision Making in an

Adversarial Environment”, Proc. AIAA conf. on Guidance Navigation and Control, (2005).

25. W.M. McEneaney and R. Singh, “Unmanned Vehicle Operations under Imperfect Informa-

tion in an Adversarial Environment ”, Proc. AIAA conf. on Guidance Navigation and Con-

trol, (2004).

26. W.M. McEneaney, “Some Classes of Imperfect Information Finite State-Space Stochastic

Games with Finite-Dimensional Solutions”, Applied Math. and Optim., Vol. 50 (2004), 87–

118.

27. W.M. McEneaney, “A Class of Reasonably Tractable Partially Observed Discrete Stochastic

Games”, Proc. 41st IEEE CDC, Las Vegas (2002).

28. W.M. McEneaney, B.G. Fitzpatrick and I.G. Lauko, “Stochastic Game Approach to Air Op-

erations”, IEEE Trans. on Aerospace and Electronic Systems, Vol. 40 (2004), 1191–1216.

29. W.M. McEneaney, “Robust/game–theoretic methods in ﬁltering and estimation”, First Sym-

posium on Advances in Enterprise Control, San Diego (1999), 1–9.

30. W.M. McEneaney, “Robust/H

∞

ﬁltering for nonlinear systems”, Systems and Control Let-

ters, 33 (1998), 315–325.

31. W.M. McEneaney and K. Ito, “Stochastic Games and Inverse Lyapunov Methods in Air

Operations”, Proc. 39th IEEE CDC, Sydney (2000), 2568–2573.

32. G.J. Olsder and G.P. Papavassilopoulos, “About When to Use a Searchlight”, J. of Math.

Analysis and Applics., Vol. 136 (1988), 466–478.

33. T. Runolfsson, “Risk–sensitive control of Markov chains and differential games”, Proceed-

ings of the 32nd IEEE Conference on Decision and Control, 1993.

34. P. Whittle, “Risk–sensitive linear/quadratic/Gaussian control”, Adv. Appl. Prob., 13 (1981),

764–777.