VEHICLE MODELS AND ESTIMATION OF CONTACT FORCES

AND TIRE ROAD FRICTION

Nacer K. M’Sirdi

LSIS, CNRS UMR 6168. Dom. Univ. St Jrme, Av. Escadrille Normandie - Niemen 13397, Marseille Cedex 20, France

Abdelhamid Rabhi

C.R.E.A, 7 Rue du Moulin Neuf, 80000 Amiens, France

Aziz Naamane

LSIS, CNRS UMR 6168. Dom. Univ. St Jrme, Av. Escadrille Normandie - Niemen 13397, Marseille Cedex 20, France

Keywords:

Vehicle dynamics, Sliding Modes observer, Robust nonlinear observers, tire forces estimation.

Abstract:

In this paper a 16 DoF vehicle model is presented and discussed. Then some partial models are considered

and justiﬁed for the design of robust estimators using sliding mode approach in order to identify the tire-

road friction or input variables. The estimations produced are based on split system equations in as cascaded

observers and estimators. The ﬁrst produces estimations of vehicle states.

1 INTRODUCTION

In recent years, the increasing demand for the safety

in car vehicles has promoted research and develop-

ment of the technology of active safety. However

more and more new active safety systems are devel-

oped and installed on vehicles for real-time monitor-

ing and observers for controlling the dynamic stability

(EBS, ABS, ESP).

Car accidents occur for several reasons which may

involve the driver or vehicle components or environ-

ment. Such situations appears when the vehicle is

driven beyond the adherence or stability limits. One

of the important factors determining vehicle dynam-

ics including safety is road friction and the tire forces

(ground-vehicle interactions). In general partial and

approximated models are used. They are not fully jus-

tiﬁed and their validity is often limited. In this work

we try to highlight some of the approximations made

and give some details allowing to evaluate what is re-

ally neglected.

Robust observers looking forward are based on

the physics of interacting systems (the vehicle, the

driver and the road). However, tire forces and road

friction are difﬁcult to measure directly and to repre-

sent precisely by some deterministic model equations.

In the literature, their values are often deduced by

some experimentally approximated models (Gustafs-

son). The knowledge of tire parameters and variables

(forces, velocities, wheel and slip), tire forces is es-

sential to advanced vehicle control systems such as

anti-lock braking systems (ABS), traction control sys-

tems (TCS) and electronic stability program (Acker-

mann)(Msirdi04)(Canudas03). Recently, many ana-

lytical and experimental studies have been performed

on estimation of the frictions and contact forces be-

tween tires and road.

We focus our work, as presented in this paper, ﬁrst

on modeling and second on on-line estimation of the

tires forces (Ackermann)(Msirdi04). We estimate the

vehicle state and identify tire forces ((Msirdi03)). The

main contribution is the emphasize of the rational be-

hind partial approximated models and the on-line es-

timation of the tire force needed for control.

Tire forces can be represented by the nonlinear

(stochastic) functions of wheel slip. The determin-

istic tire models encountered are complex and de-

pend on several factors (as load, tire pressure, en-

vironmental characteristics, etc.). This makes on

line estimation of forces and parameters difﬁcult for

vehicle control applications and detection and diag-

nosis for driving monitoring and surveillance. In

(Drakunov)(Canudas03), application of sliding mode

control is proposed. Observers based on the sliding

mode approach have been also used in (Rabhi04).

351

K. M’Sirdi N., Rabhi A. and Naamane A. (2007).

VEHICLE MODELS AND ESTIMATION OF CONTACT FORCES AND TIRE ROAD FRICTION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 351-358

DOI: 10.5220/0001636403510358

 SciTePress

In (Ray) an estimation method is based on the least

squares algorithm and combined with a Kalman ﬁlter

to estimate the contact forces. The paper of (Gustafs-

son) presents an estimation of tire/road frictions by

means of a Kalman ﬁlter. It gives relevant estimates

of the slope of µ versus slip (λ). In (Carlson) esti-

mations of longitudinal stiffness and wheel effective

radius are proposed using vehicle sensors and a GPS

for low values of the slip.

Robust observers with unknown inputs have been

shown to be efﬁcient for estimation of road pro-

ﬁle (Imine) and for estimation of the contact forces

(Msirdi04)(Rabhi04). Tracking and braking control

reduce wheel slip. This can be done also by means of

its regulation while using sliding mode approach for

observation and control.(Msirdi04)(Rabhi04). This

enhances the road safety leading better vehicle ad-

herence and maneuvers ability. The vehicle control-

lability in its environment along the road admissible

trajectories remain an important open research prob-

lem.

The proposed estimation procedure has to be ro-

bust enough to avoid model complexity. It can then

be used to detect some critical driving situations in

order to improve the security. This approach can be

used also in several vehicle control systems such as

Anti-look Brake Systems (ABS), traction control sys-

tem (TCS), diagnosis systems, etc... The main char-

acteristics of the vehicle longitudinal dynamics were

taken into account in the developed model used to de-

sign robust observer and estimations. The estimations

are produced using only the angular wheel position

as measurement by the specially designed robust ob-

server based on the super-twisting second-order slid-

ing mode. The proposed estimation method is veri-

ﬁed through simulation of one- wheel model (with a

”Magic formula” as tire model). In a second step of

validation we present some application results (on a

Peugeot 406) showing an excellent reconstruction of

the velocities, tire forces and estimation of wheel ra-

dius.

2 VEHICLE MODELING

2.1 Complete 16 DoF Model

In literature, many studies deal with vehicle model-

ing (Kien)(Ramirez)(Mendoza). This kind of systems

are complex and nonlinear composed with many cou-

pled subsystems: wheels, motor and system of brak-

ing, suspensions, steering, more and more inboard

and imbedded electronics. Let us represent the ve-

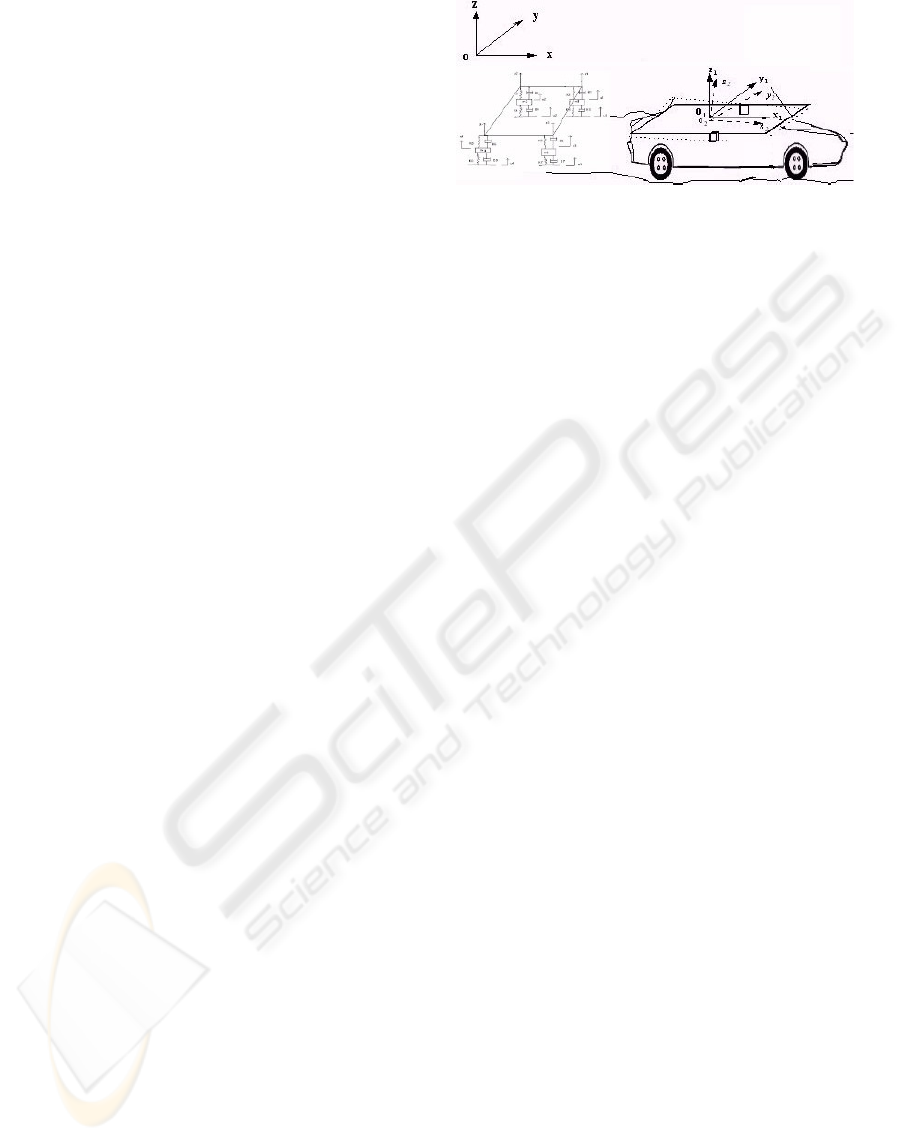
hicle (like eg a Peugeot 406) by the scheme of ﬁgure

Figure 1: Vehicle dynamics and reference frames.

1 and deﬁne the following notations.

The vehicle body receives as excitations external

forces and moments following the three axes: - Lon-

gitudinal, - Lateral, - Vertical. These come from in-

teraction of the wheels and road, from perturbations

(wind for example), gravity and vehicle drive line. Let

us consider the basic reference ﬁxed frame R. We can

consider the vehicle as made of 5 sub-systems: chas-

sis whit 6 DoF and then 4 wheels with their suspen-

sions. Each of the rear wheels has 2 DoF. The front

ones are driven wheels with 3 DoF each. Then we

have 16 DoF. Let the generalized variables be in the

vector q ∈ R

, deﬁned as

=[x, y, z, θ

, θ

, z

, δ

, ϕ

]

where x, y, et z represent displacements in longitu-

dinal, lateral and vertical direction. angles of roll,

pitch and yaw are θ

, θ

et θ

respectively. The

suspensions elongations are noted z

: (i = 1..4). δ

stands for the steering angles (for wheels numbered

as i = 3, 4), ﬁnally ϕ

: are angles wheels rotations

(i = 1..4.). Vectors ˙q, ¨q ∈ R

are respectively veloci-

ties and corresponding accelerations. M(q) is the in-

ertia matrix and C(q, ˙q) ˙q are coriolis and centrifugal

forces. The gravity term is G . Suspensions forces

are V (q, ˙q) = K

˙q + K

q with respectively damping

and stiffness matrices K

, K

. We can deﬁne as dy-

namic equations of the vehicle by applying the prin-

ciples fundamental of the dynamics (see (Beurier)):

Γ + J

F = M

q +C(q,

q + Kq + G (1)

with as parameters only to give an idea

M =







1,1

1,2

1,3

0 0

2,1

2,2

2,3

2,4

2,5

3,1

3,2

3,3

0 0

4,2

4,4

5,2

0 0

5,5







C =







0 0

0 0 0

0 0







ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

352

and J







1,1

1,2

1,3

1,4

2,1

2,2

2,3

2,4

3,1

3,2

3,3

0 0 0 J

4,4

0 0 0 0







This is just to show that we can decompose our

system as coupled subsystems. Let us say ﬁve cou-

pled subsystems, that we have considered in our pre-

vious works. This has been computed using a sym-

bolic computation software considering 16 general-

ized variables: 6 for position and orientation of body,

4 as suspensions ones, 2 for front wheels steering and

4 as wheels rotations. The matrices M, C and K are

of dimensions 16 × 16. F is input forces vector acting

on wheels, it has 12 components(3 forces ( longitu-

dinal, lateral and normal) × 4 wheels), Γ represent

extra inputs for perturbations.. In the following ap-

plication this model has been reduced and simpliﬁed

assuming as nominal behavior a normal driving situ-

ation (Msirdi03).

2.2 Coupled Sub Models

We can split the previous model, without approxima-

tions, in ﬁve parts as follows. This leads us to the

body’s translations dynamics:





T T





















+ (2)





















(3)

Rotations and orientation motions of the body:

























































































Suspensions dynamics:







10F







1,3









2,3









3,3





































































(4)

The previous 16 DoF model is then equivalent to:













= M































.ξ



















In the last expression, we can remark that splitting

the model can be realized and this model is helpful,

when using reduced models, to identify what is ne-

glected regard to our proposed nominal model with

16 DoF. The dynamic equations can be reduced, in

case where we assume that motion is normal driving

in a normal staith road, to translations and rotations

of the body, and wheels plus suspension motions. For

translations we ﬁnd often in literature:

∑

(5)

where m is the total mass of the vehicle and v =

, v

]

describe the vehicle velocities along x, y,

z. In the left hand side of this approximate model

are the forces

∑

and

∑

applied in direc-

tions of x, y and z and the balance of the moments

(

∑

), give rotations following the three

directions x, y and z, is given by:

















∑





(6)

The wheel angular motions can be written:

f l

− R

x f 1

) (7)

f r

− R

x f 2

)

− R

xr1

)

− R

xr2

)

VEHICLE MODELS AND ESTIMATION OF CONTACT FORCES AND TIRE ROAD FRICTION

353

with ω

and ω

are the rotation velocities of the front

and rear wheel, C

is the motor couple applied at

wheel i and T

is the braking couple applied at wheel

i. Let r

be the distance between the center of grav-

ity and the front axis and r

the distance between the

center of gravity and the rear axis.

2.3 Partial Models

The complete model is difﬁcult to use in control ap-

plications. It involves several variables which are not

available for measurement or not observable. The

most part of applications deal with simpliﬁed and par-

tial models. Let us consider, for our robust observer,

the simpliﬁed motion dynamics of a quarter-vehicle

model, capturing only nominal behavior (Msirdi04)

(Msirdi03). This model retains the main characteris-

tics useful for the longitudinal dynamic. For a global

application, this method can be easily extended to the

complete vehicle and involve the four coupled wheels.

The amount of neglected parts in the modeling can be

considered to evaluate robustness of proposed estima-

tors.

Applying Newton’s law to one isolated wheel

gives:.

= F

ω = T − rF

where m is the vehicle mass and J

, r are the in-

ertia and effective radius of the tire respectively. v

is the linear velocity of the vehicle, ω is the angular

velocity of the considered wheel. T is the accelerat-

ing (or braking) torque, and F

is the tire/road friction

force. The tractive (respectively braking) force, pro-

duced at the tire/road interface when a driving (brak-

ing) torque is applied to pneumatic tire, has oppo-

site direction of relative motion between the tire and

road surface. This relative motion exhibits the tire slip

properties. The wheel-slip is due to deﬂection in the

contact patch. The longitudinal wheel slip is gener-

ally called the slip ratio and is described by a kine-

matic relation as (Carlson).

λ =

− v

max(v

, v

)

(8)

where v

is the wheel velocity. Representing the

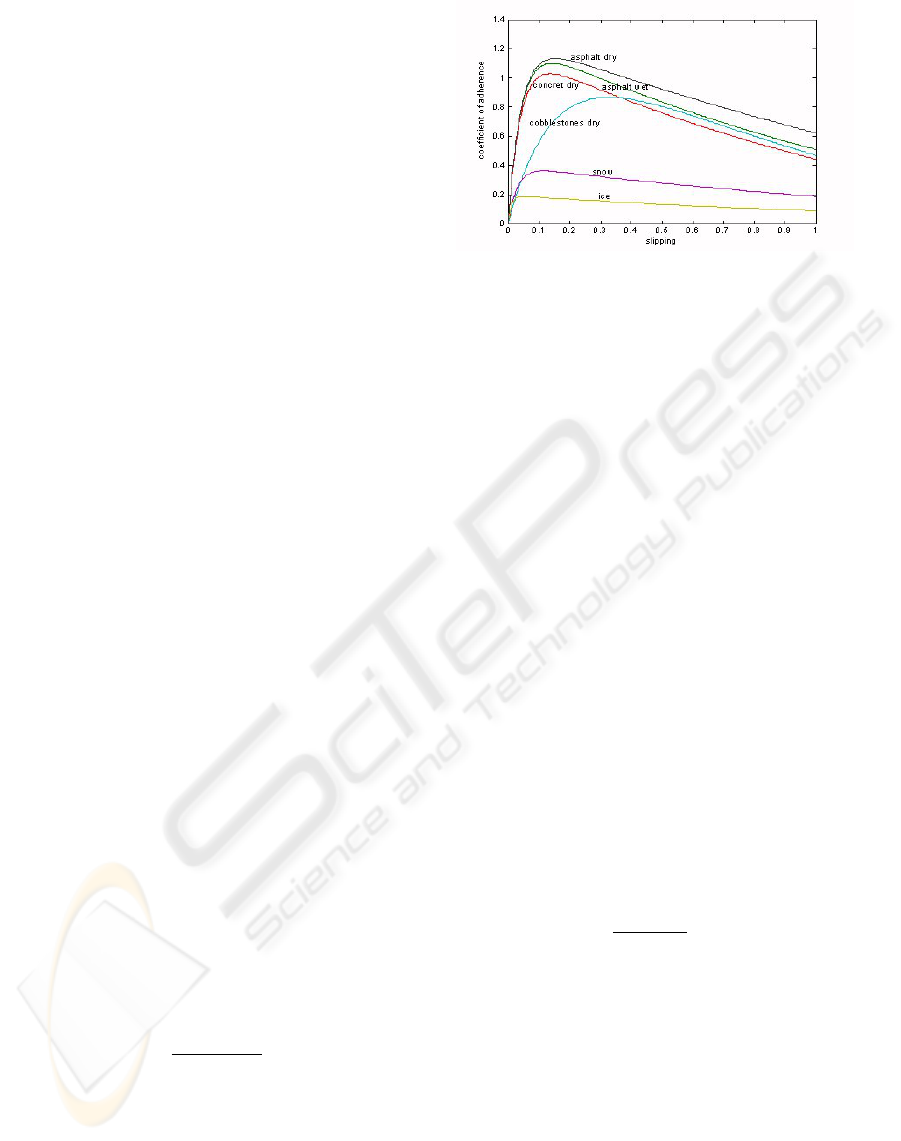
adhesion coefﬁcient as a function of the wheel slip

yields the adhesion characteristic µ(λ), which de-

pends on the road surfaces as shown in the following

ﬁgure 2.

The ﬁgure 2 shows the relations between coefﬁ-

cient of road adhesion µ and longitudinal slip λ for

Figure 2: Wheel slip.

different road surface conditions. It can be observed

that all curves µ(λ) start at µ = 0 for zero slip, which

corresponds to the non-braking and non accelerating,

free rolling wheel. With a linear increasing slip ratio

from 3% to 20%. Beyond this maximum value the

slope of the adhesion characteristic is maximum and

then slope becomes negative. At a slip ratio of 100%

the wheel is completely skidding, which corresponds

to the locking of the wheel. The adhesion character-

istic plays an essential role for both the design and

the validation of ABS. Overall, to improve the perfor-

mance of an ABS it is desirable to have some real-

time information about the adhesion characteristic.

By assuming that the longitudinal forces are pro-

portional to the transversal ones, we can expressed

theses forces as follows, where F

is the vertical force

of the wheel.

= µF

(9)

The vertical forces that we use in our model

are function of the longitudinal acceleration and the

height of the center of gravity. The vertical force can

be represented as:

Fz =

2(l

+ l

)

(gl

− h

) (10)

where h is the height of the center of gravity, l

is the distance between the center of gravity and the

front axis center of gravity and l

is the distance be-

tween the center of gravity and the rear axis center of

gravity.

3 OBSERVER DESIGN

The sliding mode technique is an attractive approach

(Davila). The primary characteristic of SMC is that

the feedback signal is discontinuous, switching on

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

354

one or several manifolds in the state-space. In what

follows, we use a second order differentiator in order

to derive robust estimates of the tire road friction.

3.1 High Order Sliding Mode Observer

(HOSM)

In this part we will use a Robust Differentiation

Estimator (RDE) to deduce our robust estimations.

Consider a smooth dynamics function, s(x) ∈ R.

The system containing this variable may be closed

by some possibly-dynamical discontinuous feedback

where the control task may be to keep the output

s(x(t)) = 0. Then provided that successive total time

derivatives s,

s...s

(r−1)

are continuous functions of

the closed system state space variables, and the t-

sliding point set is non-empty and consist locally of

Filippov trajectories.

s =

s = ... = s

(r−1)

= 0 (11)

is non-empty and consists locally of Filippov tra-

jectories. The motion on set (Filippov)(Utkin99)

is called r-sliding mode (r

-order sliding mode)

(Orlov)(Levant).

The HOSM dynamics converge toward the origin

of surface coordinates in ﬁnite time always that the or-

der of the sliding controller is equal or bigger than the

sum of a relative degree of the plant and the actuator.

To estimate the derivatives s

and s

without its direct

calculations of derivatives, we will use the 2

-order

exact robust differentiator of the form (Levant)

= v

= z

− λ

− s

sign(z

− s

)

= v

= −λ

sign(z

− v

)

sign(z

− v

) + z

= −λ

sign(z

− v

)

where z

, z

and z

are the estimate of s

, s

and

, respectively, λ

> 0, i = 0, 1, 2. Under condition

> λ

the third order sliding mode motion will

be established in a ﬁnite time. The obtained estimates

are z

= s

and z

= s

then they can be

used in the estimation of the state variables and also

in the control.

3.2 Cascaded Observers - Estimators

In this section we use the previous approach to build

an estimation scheme allowing to identify the tire

road friction. The estimations will be produced in

three steps, as cascaded observers and estimator, re-

construction of information and system states step by

step. This approach allow us to avoid the observ-

ability problems dealing with inappropriate use of the

complete modeling equations. For vehicle systems it

is very hard to build up a complete and appropriate

model for global observation of all the system states

in one step. Thus in our work, we avoid this prob-

lem by means of use of simple and cascaded models

suitable for robust observers design.

The ﬁrst step produces estimations of velocities.

The second one estimate the tire forces (vertical and

longitudinal ones) and the last step reconstruct the

friction coefﬁcient.

The robust differentiation observer is used for es-

timation of the velocities and accelerations of the

wheels. The wheels angular positions and the veloc-

ity of the vehicles body v

, are assumed available for

measurements. The previous Robust Estimator is use-

ful for retrieval of the velocities and accelerations.

Step:

θ = v

ω − λ



θ −



sign(θ −

θ)

ω = v

ω − λ

sign(

ω − v

)

sign(

ω − v

)

ω = −λ

sign(

ω − v

)

The convergence of these estimates is guaranteed

in ﬁnite time t

Step: In the second step we can estimate the

forces F

and F

. Then to estimate F

we use the fol-

lowing equation,

ω = T − R

e f

(12)

In the simplest way, assuming the input torques

known, we can reconstruct F

as follows:

(T − J

ω)

e f

(13)

ω is produced by the Robust Estimator (RE). Note

that any estimator with output error can also be used

to enhance robustness versus noise. In our work, in

progress actually, the torque T will be also estimated

by means of use of additional equation from engine

behavior related to accelerating inputs.

After those estimations, their use in the same time

with the system equations allow us to retrieve de ver-

tical forces F

as follows. To estimate F

we use the

following equation

2(l

+ l

)

(gl

− h.

) (14)

is produced by the RE.

Step: At this step it only remains to estimate

the adherence or friction coefﬁcient. To this end we

VEHICLE MODELS AND ESTIMATION OF CONTACT FORCES AND TIRE ROAD FRICTION

355

assume the vehicle rolling in a normal or steady state

situation in order to be able to approximate this coef-

ﬁcient by the following formula

µ =

(15)

4 SIMULATION AND

EXPERIMENTAL RESULTS

In this section, we give some realistic simulation re-

sults in order to test and validate our approach and

the proposed observer. In simulation, the state and

forces are generated by use of a car simulator called

VeDyna (VEDYNA). In this simulator the model in-

volved is more complex than the one of 16 DoF pre-

sented in the ﬁrst part of the paper. Comparind the

simpliﬁed model to the 16 DoF one, let us evaluate

the robustness of estimation The VeDyna simulated

brake torque is shown in ﬁgure 3.

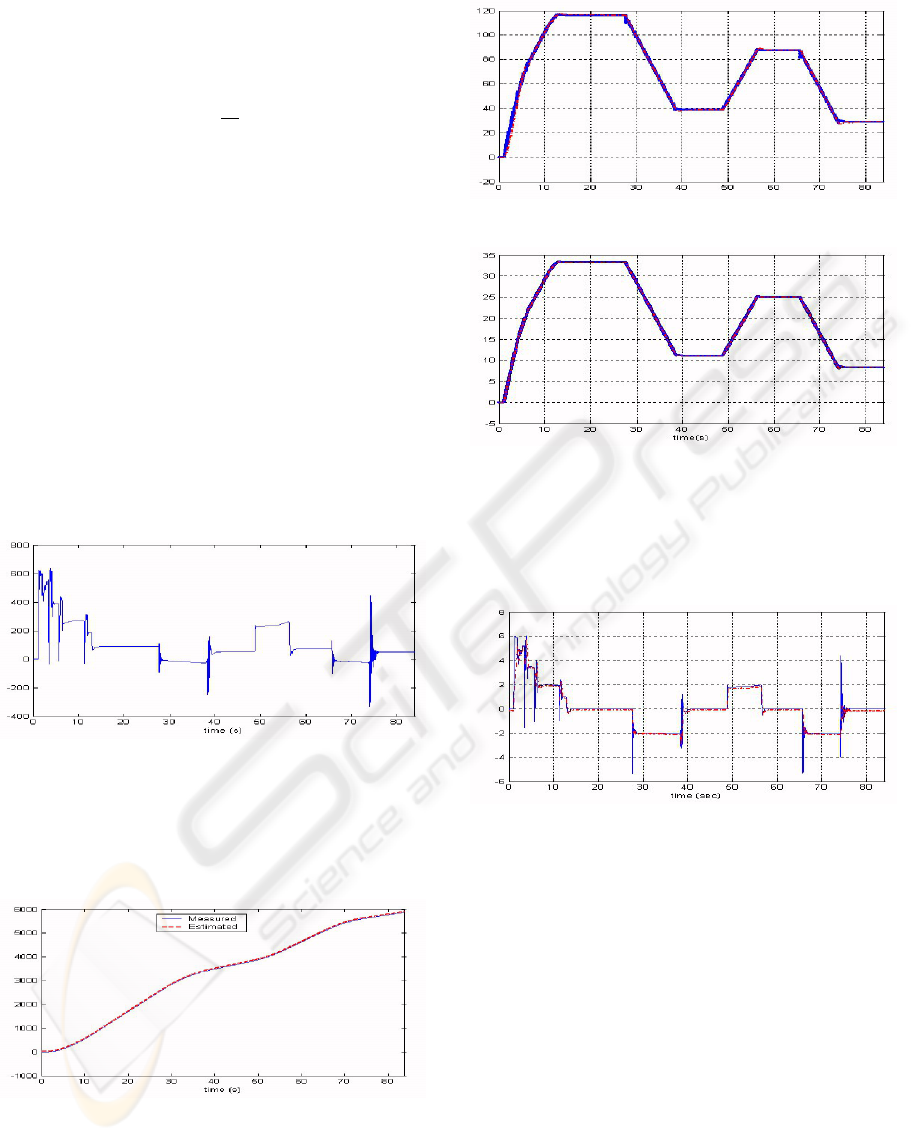
Figure 3: Braking torque.

Figure 4 shows the measured and estimated wheel

angular position. This signal is used to estimate ve-

locities and accelerations. Figure 4 shows the esti-

Figure 4: Angular displacements.

mated wheel angles. In the ﬁgure 6, we represent

the estimation of vehicle velocity. The ﬁgure shows

the good convergence to the actual vehicle velocity.

Figure 7 shows the obtained vehicle acceleration. The

Figure 5: Angular Velocity.

Figure 6: Vehicle velocity.

observer allows a good estimation of angular velocity

and acceleration. The last step gives us the estimated

Figure 7: Estimated and measured acceleration.

longitudinal forces F

and normal forces F

which are

presented in ﬁgure 8 and 9. Finally road friction

coefﬁcient is deduced and presented in ﬁgure (10).

5 CONCLUSION

In this work we have tried to highlight all approxima-

tions made in general when using simpliﬁed models

and this paper gives some details allowing to evaluate

what is really neglected. In second part od this paper,

we have proposed an efﬁcient and robust estimator

baser on the second order sliding mode differentiator.

This is used to build an estimation scheme allowing to

identify the tire road frictions and input forces which

are non observable when using the complete model

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

356

Figure 8: Longitudinal force.

Figure 9: Normal force F

and standard sensors. The estimations produced ﬁ-

nite time converging measurements of model inputs,

in three steps by cascaded observers and estimators.

This method shows very good performances in simu-

lations conducted using a more complex model (than

the 16 DoF one) involved in VeDyna car simulator.

Tire forces (vertical and longitudinal ones) are also

estimated correctly. Simulation results are presented

to illustrate the ability of this approach to give es-

timation of both vehicle states and tire forces. The

robustness versus uncertainties on model parameters

and neglected dynamics has also been emphasized in

simulations. Application of this approach with inclu-

sion of torque estimation using a simpliﬁed model for

the engine behavior, is in progress.

ACKNOWLEDGEMENTS

This work has been done in a collaboration managed

by members of the LSIS inside the GTAA (research

group supported by the CNRS).

Thanks are addressed to the LCPC of Nantes for

experimental data and the trials with their vehicle

Peugeot 406.

Figure 10: Road friction.

REFERENCES

F. Gustafsson, ”Slip-based tire-road friction estimation”,

Automatica, vol 33, no. 6, pp. 1087-1097, 1997.

J. Ackermann ”Robust control prevents car skidding. IEEE

Control systems magazine, V17, N3, pp23-31, 1997

N. K. M’sirdi, A. Rabhi, N. Zbiri and Y. Delanne. VRIM:

Vehicle Road Interaction Modelling for Estimation of

Contact Forces. Accepted for TMVDA 04. 3rd Int.

Tyre Colloquium Tyre Models For Vehicle Dynamics

Analysis August 30-31, 2004 University of Technol-

ogy Vienna, Austria

C. Canudas de Wit, P.Tsiotras, E.Velenis, M.Basset,

G.Gissinger. Dynamic Friction Models for Road/Tire

Longitudinal Interaction. Vehicle Syst. Dynamics

2003. V39, N3, pp 189-226.

Laura Ray. Nonlinear state and tire force estimation for ad-

vanced vehicle control. IEEE T on control systems

technology, V3, N1, pp117-124, march 1995.

Nacer K. M’Sirdi. Observateurs robustes et estimateurs

pour l’estimation de la dynamique des v

ehicules et du

contact pneu - route. JAA. Bordeaux, 5-6 Nov 2003

S. Drakunov, U. Ozguner, P. Dix and B. Ashraﬁ. ABS con-

trol using optimum search via sliding modes. IEEE

Trans. Control Systems Technology, V 3, pp 79-85,

March 1995.

A. Rabhi, H. Imine, N. M’ Sirdi and Y. Delanne. Observers

With Unknown Inputs to Estimate Contact Forces and

Road Proﬁle AVCS’04 International Conference on

Advances in Vehicle Control and Safety Genova -

Italy, October 28-31 2004

Christopher R. Carlson. Estimation With Applications for

Automobile Dead Reckoning and Control. PhD the-

sis, University of STANDFOR 2003.

U. Kiencken, L. Nielsen. Automotive Control Systems.

Springer, Berlin, 2000.

Mendoza, Sur la mod

elisation et la commande des

ehicules automobiles, Th

ese, Juillet 1997.

H. Imine, N. M’Sirdi, L. Laval, Y. Delanne - Sliding Mode

Observers for Systems with Unknown Inputs: Appli-

cation to estimate the Road Proﬁle. A para

ıtre dans

ASME, Journal of Dynamic Systems, Measurement

and Control en mars 2003.

VEHICLE MODELS AND ESTIMATION OF CONTACT FORCES AND TIRE ROAD FRICTION

357

R. Ramirez-Mendoza. Sur la mod

elisation et la commande

des v

ehicules automobiles. PHD thesis Institut Na-

tional Polytechnique de Grenoble, Laboratoire d Au-

tomatique de Grenoble 1997.

G. Beurier. Mod

elisation et la commande de syst

eme. PHD

thesis LRP. UPMC Paris 6, 1998.

J. Davila and L. Fridman. “Observation and Identiﬁca-

tion of Mechanical Systems via Second Order Slid-

ing Modes”, 8th. International Workshop on Variable

Structure Systems,September 2004, Espana

A. Levant, ”Robust exact differentiation via sliding mode

technique”, Automatica, vol. 34(3), 1998, pp 379-384.

A. F. Filippov, Differential Equations with Discontin-

uous Right-hand Sides, Dordrecht, The Nether-

lands:Kluwer Academic Publishers; 1988.

V. Utkin, J. Guldner, J. Shi, Sliding Mode Control in Elec-

tromechanical Systems, London, UK:Taylor & Fran-

cis; 1999.

J. Alvarez, Y. Orlov, and L. Acho, ”An invariance principle

for discontinuous dynamic systems with application

to a coulomb friction oscillator”, Journal of Dynamic

Systems, Measurement, and Control, vol. 122, 2000,

pp 687-690.

Levant, A. Higher-order sliding modes, differentiation and

output-feedback control, International Journal of Con-

trol, 2003, Vol.76, pp.924-941

Simulator VE-DYNA. www.tesis.de/index.php.

APPENDIX

Deﬁnition of the matrices involved.in the model.





1,1

0 0

0 M

2,2

0 0 M

3,3









1,4

1,5

1,6

2,4

3,5

2,6

0 M

3,5

3,6





;





1,7

1,8

1,9

1,10

2,7

2,8

2,9

2,10

3,7

3,8

3,9

3,10





;





4,7

4,8

4,9

4,10

5,7

5,8

5,9

5,10

6,7

6,8

6,9

6,10









4,11

4,12

4,13

5,11

5,12

5,13

0 0 0





2,5





4,14

4,15

4,16

5,14

5,15

5,16

0 M

6,15

6,16





2,2





4,4

4,5

4,6

5,4

5,5

5,6

6,4

6,5

6,6





;

3,3







7,7

0 0 0

0 M

8,8

0 0

0 0 M

9,9

0 0 0 M

10,10







;

4,4





11,11

0 0

0 M

12,12

0 0 M

13,13





5,5





14,14

0 0

0 M

15,15

0 0 M

16,16





ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

358