To Add with Caution — Decreasing a Swarm Robotics’

Efﬁciency by Imprudently Enhancing the Robots’

Capabilities

⋆

Yaniv Altshuler

, Israel A. Wagner

1,2

and Alfred M. Bruckstein

Computer Science Department, Technion, Haifa 32000 Israel

IBM Haifa Labs, MATAM, Haifa 31905 Israel

Abstract. This work discusses the common opinion among robotics systems’

designer, assuming that for a given assignment and robotics system, enhancing

the robots by increasing their physical capabilities, may only result in an im-

provement in the overall performance of the system (albeit small). Therefore, a

designer may rely on existing designs prepared in the past, and by continuously

adding resources to the robots, ﬁnally achieve the overall system’s performance

he is interested in. As it can be shown, this assumption is wrong, as it may not only

lead to a zero increase in the performance, but even to a new system, comprising

far more advance (and expensive) robots, which achieve much worse results than

the original system. The work presents an example concerning the problem of

multi-robots exploration of a graph, in which adding communication features to

the robots causes the entire system’s performance to drop signiﬁcantly.

1 Introduction

In recent years signiﬁcant research efforts have been invested in design and simulation

of multi-agent robotics and intelligent swarms systems — see e.g. [1–3] or [4–6] for

biology inspired designs (behavior based control models, ﬂocking and dispersing mod-

els and predator-prey approaches, respectively), [7–10] for economics applications and

[11] for a physics inspired approach).

Tasks that have been of particular interest to researchers in recent years include syn-

ergetic mission planning [12], fault tolerance [13], swarm control [14], human design of

mission plans [15], role assignment [16], multi-robot path planning [17], trafﬁc control

[18], formation generation [19], formation keeping [20], exploration and mapping [21],

cleaning [22] and dynamic cleaning [23] and target tracking [24].

Hitherto, in the design of robotics systems, and speciﬁcally, in the design and imple-

mentation of multi-robotics systems, there exists an implicit yet common assumption

concerning the monotonicity of the relation between the strength of the robots’ capa-

bilities (in terms of memory, sensors’ accuracy, communication capabilities, etc’), and

the overall performance this system achieves given a speciﬁc goal and an algorithm

⋆

This research supported in part by the Ministry of Science Infrastructural Grant No. 3-942 and

the Devorah fund.

Altshuler Y., A. Wagner I. and M. Bruckstein A. (2007).

To Add with Caution —Decreasing a Swarm Robotics’ Efﬁciency by Imprudently Enhancing the Robots’ Capabilities.

In Proceedings of the 3rd International Workshop on Multi-Agent Robotic Systems, pages 24-33

 SciTePress

for achieving it. In other words, is it widely assumed that given a multi-robotic sys-

tem comprising robots of certain features, designed for accomplishing a speciﬁc goal,

enhancing the robots’ features, or alternatively, supplying those robots with additional

capabilities, may only improve the performance these robots achieve when facing the

same problem.

Although appealing, this approach for performance improvement as a result of

tweaking existing multi-robotic designs by merely enhancing the robots’ capabilities

should be avoided, as such endeavors may result not only in spending expensive re-

sources on futile attempts to increase the system’s performance, but even in dramatic

decrease in the overall performance of the system. Although strange at ﬁrst, this phe-

nomenon can be examined by systematically increasing some of the features of agents

designed for a given task, for example — the physical exploration of a graph, while

observing the changes in the performance of this group of agents.

One of the most interesting challenges for a robotics swarm system is the design and

analysis of a multi-robotics system for searching and exploration (in either known or

unknown areas). For example, works discussing cooperative searching tasks for static

or dynamic targets can be found in [25–31] whereas examples for cooperative coverage

of given regions are presented in [32–35].

This work presents a multi-agents system designed for exploring an unknown graph,

by physically moving along its vertices. The problem and its model is described in

Section 2. Once a system following the basic exploration algorithm was implemented

and its performance measured, a change in its robots’ features was made, namely —

their technical speciﬁcation was upgraded. The ﬁrst upgrade was adding communica-

tion equipment to the robots, allowing them to share the information they acquire by

traveling the graph. The second change was increasing the robots’ sensors’ range, in an

effort to increase the accuracy of the information the robots use in order to plan their

future actions, and as a result, to increase the system’s efﬁciency. After these changes

in the robots’ speciﬁcation were implemented, the performance of the new group was

tested and analyzed. Note that the exploration algorithm itself, which was found to be

achieve the best results in the original group of robots, was not changed during this

process.

Surprisingly, the analyzed results of this experiment showed that not only that the

upgraded group of robots did not achieve superior results compared to the original group

of robots, but in fact, the exploration time required by this group was much longer

compared to the exploration time of the original group of robots. This was true both

for the robots with increased communication capabilities, as well as for the robots with

increased sensors’ range. The results and their analysis appears in Section 3.

2 Physical Graph Exploration

2.1 Physical Graphs

A physical graph denotes a graph G(V, E) in which information regarding its vertices

and edges is extracted using I/O heads, or mobile agents, instead of the “random access

extraction” which is usually assumed in graph theory. These agents can physically move

between the vertices of V along the edges of E, according to a predeﬁned, or an on-line

algorithm or algorithm.

Moving along an edge e, however, require a certain travel effort (which might be

a constant time, or alternatively, consumes a constant amount of fuel). Thus, the com-

plexity of algorithms which work on physical graphs is measured by the total travel

efforts required, which equals the number of edges traveled by the agents. We assume

that each edge requires exactly one unit of travel effort.

Physical graphs are conveniently used in order to represent many “real world prob-

lems”, in which the most efﬁcient algorithm is not necessarily the one whose compu-

tational complexity is the minimal, but rather one in which the agents travel along the

minimal number edges. Notice that while an algorithm which assumes a random access

data extraction (from now on be referred to as random access algorithm) may read and

write to the vertices of G at any order, an algorithm which assumes a physical data

extraction (referred to as a physical algorithm) must take into account the distance be-

tween two sequential operations. The reason for this is that the use of a random access

algorithm is performed using a processing unit and random access memory, whereas

the use of a physical algorithm is actually done in the physical environment (or a simu-

lated physical environment, which maintain the information access paradigm). Thus, a

random access algorithm can access any vertex of the graph in O(1), while a physical

algorithm is conﬁned to the distances imposed by the physical metric.

For example, for u, v ∈ V , let us assume that the distance between v and u in G

is 5. Then if after a ‘read’ request from u, the algorithm orders a ‘write’ request to

v, this process will take at least 5 time steps, and will consume at least 5 effort units.

Furthermore, depending on the model assumed for the mobile agents knowledge base,

this operation may take even longer, if, for example, the agents are not familiar with the

shortest path from u to v, but rather know of a much longer path connecting the two.

2.2 Problem Description

For a given graph G, let each vertex v ∈ V contain some small data storage unit v

capable of storing information saved by agents traveling through v. In time t = 0, let

= ∅ for every v ∈ V .

Let us assume that whenever a robot a goes through a vertex v, is saves at least its

id number and the time of the visit in v

While in vertex v, a robot a can detect the number of other robots located in v or

in its immediate surroundings, and the number of edges going out from v. In addition,

every edge has a unique id number, written on it (very similar to a web of roads, while

each road has a unique name or a number, and that for ﬁnding out where this road leads,

one must travel along it). In addition, the robot has access to all the data stored in v

Given a group of k robots (or agents), capable of physically traveling the graph,

according to the model described in Section 2.1, while each robot can move along a

single edge per time-step, we are interested in the goal state G

g oal

in which v

6= ∅ for

every v ∈ V , meaning — that every vertex was visited at least once by some robot. We

are interested that the time in which G

g oal

is achieved will be minimal (namely, a short

exploration as possible).

This abstract problem may ne used for simulating many common problems in the

ﬁeld of multi robotics, for example — a search and rescue mission of unknown number

of survivors in a pre-deﬁned (or alternatively — unknown) area, distributed autonomous

mining, a de-centralized anti-virus mechanism scanning and cleaning a computer net-

work, and so on.

2.3 Exploration Algorithm

Every robot a is equipped with a data structure a

, capable of storing lists of vertices,

edges and locations of other robots. At t = 0 all data structures are initialized as empty.

At each time step, a robot located in vertex v follows the exploration algorithm, which

controls the vertex u this robot will move to (notice that v must be a neighbor of u).

Once a robot a reaches a certain vertex v, it integrates the information stored both in

and in a

, so that at the end of this process, both contains the same information.

Whenever an inconsistency is found regarding the status of a certain vertex, edge or

robot, it is solved according to the most recent entry concerning this item.

It can be seen that throughout the movement along the graph generated by the ex-

ploration algorithm, combined with the information proliferation process executed by

using the robots as a tool for transferring the information between the vertices, a more

and more accurate image of G is generated in the vertices storage components, as well

as in the robots’ data structures. This accuracy in turn, is supposed to contribute to the

efﬁciency of the robots, by accelerating the exploration process.

The exploration algorithm selected for this mission can generally be described as

the following pseudo-code, executed by each robot independently :

1. For every v in V

′

, when V

′

is the list of vertices currently known to the robot,

perform the following :

(a) Let unvisited(v) denote the number of edges of v, currently known to the robot,

whose destination from v is currently unknown.

(b) Let distance(v) denote the length of the shortest path between v and the current

location of the robot, comprising only vertices and edges currently known to

the robot.

calculated based on the knowledge the robot has of the structure of G in the

vicinity of v and of the knowledge the robot has concerning the whereabouts

of the other robots.

(d) Let robots-neighborhood(v ) denote the probability that other robots are located

at the close vicinity of v. This is calculated similarly to robots(v).

(e) Calculate the combined score of v, as a weighted average of unvisited(v),distance(v),

robots(v),robots-neighborhood(v). Note that the selection of the averaging vec-

tor is an extremely important feature of the exploration algorithm.

2. Let v

best

be the vertex whose combined score is the highest.

3. Start walking towards v

best

(at the pace of a single edge per time-step).

4. When reaching v

best

, randomly select one of the edges going out from v

best

with

an unknown destination, and move towards it.

For choosing the best averaging vector, many simulation were executed, testing a

variety of weights values. Finally, several vectors were found, which were both robust

(in terms of a relatively high score for the scenarios in which they function at their

worst) and potent (in terms of the ability to score extremely high in scenarios in which

they were at the best). A detailed discussion concerning the speciﬁc vectors and the

process of selecting them will appear in an extended version of this work, currently

under preparation.

2.4 Upgrades

Once the performance of a group of k robots implementing the exploration algorithm

with the chosen averaging vectors were available, the robots’ technical speciﬁcation

was enhanced by two major aspects.

First, a component simulating a full-range broadcasting equipment was added to

each robots, allowing it to instantly update and receive information from the other robots

of the group. The result of this upgrade if essentially the ability of a robot which calcu-

lates the heuristic score of the vertices of the graph, trying to decide its destination, to

use the most accurate information, as it is known to any of the robots. This upgrade was

expected to boost the performance of the robots, since often, a robot becomes isolated

in the graph, traveling among previously visited vertices, while valuable information

concerning this area of the graph was already gathered by the rest of the robots, and is

unavailable for this robot.

The second upgrade was the addition of a full-range sensor, capable of scanning

the entire graph G. Notice that this component transform each robot to an omniscient

unit, making both communication equipment and data storage components along the

vertices unnecessary (as at any given time, each robot can access any information it

requires, with complete accuracy). This upgrade was expected to increase even further

the robots’ efﬁciency, and as a result — to decrease their exploration time.

3 Results

A simulation of the three types of robots was built. The exploration algorithm was tested

on Erd

os-Renyi random graphs G ∼ G(n, p) where G has n vertices, and each pair of

vertices form an edge in G with probability p independently of each other.

Surprisingly, once examining the exploration times of the upgraded robots, and

comparing them to those of the original groups of robots, the exploration times of the

original groups were signiﬁcantly lower than those of the upgraded robots. An example

of this phenomenon appears in Figure 1.

It can easily be seen that although there is almost no difference between the per-

formance of the broadcasting robots and the omniscient robots, both had much longer

exploration times than the the original group of the “simple robots”, which lacked ei-

ther communication or extreme sensing capabilities. It is interesting to mention that this

phenomenon became increasingly more intense as the graphs became more and more

dense, that is — as p, the edge probability, was increased. Furthermore, as the group

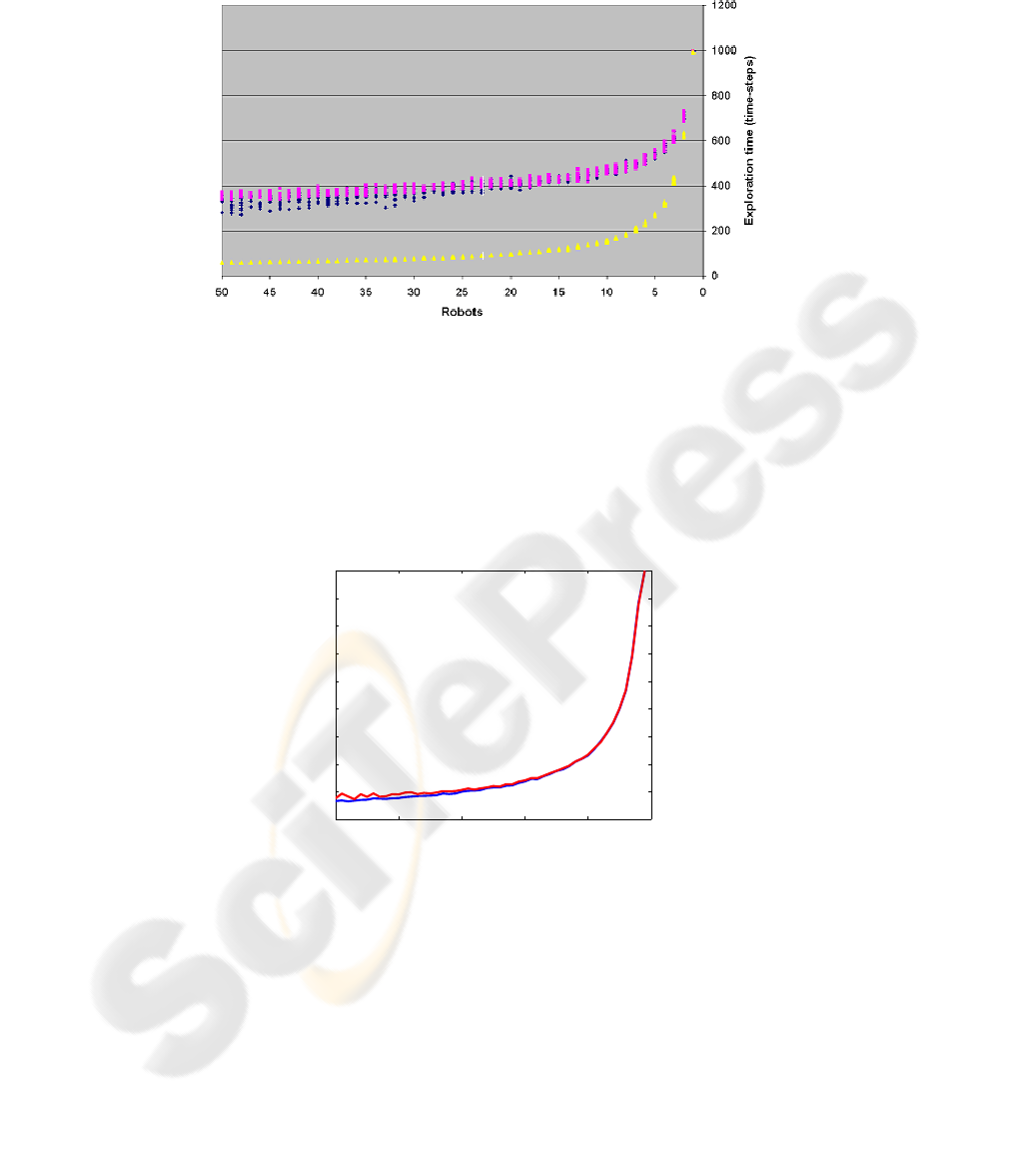
Fig.1. This chart depicts the range of exploration times of three groups of robots, tested in a

variety of random graphs. The lower yellow curve represents the exploration time of the orig-

inal group, comprising “basic robots”, to whom the exploration algorithm used was originally

designed. The blue and purple curves represent the exploration times of the two groups of “up-

graded robots”, whose communication and sensing capabilities were enhanced, respectively.

01020304050

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Fig.2. The graph represents the ratio between exploration times of the “basic robots” and aver-

aged results of the two groups of “upgraded robots” (the red curve represents the robots which

were assigned a full-range broadcasting capability, while the blue curve represents the robots

whose sensors’ range was increased). As the number of robots (represented as the X axes) in-

creases, the ratios discussed decreases. For groups of over 30 robots, the upgraded robots achieve

an efﬁciency of approximately 20% than this of the simple robots (namely, 5 times larger an

exploration time).

of robots became larger, the inefﬁciency of the upgraded robots became signiﬁcantly

clearer, as can be seen in Figure 2

After analyzing the reasons for these unexpected results, by reconstructing the in-

ternal decisions’ considerations made by each robot in the various scenarios, it was

discovered that the improved accuracy of the robots caused an undesired synchronicity

effect, grouping the robots into a small and tightly packed group. As a result, the robots

were not able to efﬁciently explore many parts of the graphs, as they moved heavily,

delaying each other from exposing unrevealed valuable information (such as shorter

paths between vertices).

As it turned out, the reason for this phenomenon was that the averaging vector,

found to be best for the original group of robots, contained a positive weight for the

robots(v) element. The positive contribution of this element to the overall score of some

vertex v intended to assist the scattered robots to remain loosely tied, in order to sustain

the proliferation of valuable information. As the accuracy of the robots’ knowledge

increased (ﬁrst by providing them a accurate information concerning the other robots’

whereabouts at any given time, and later by providing them even the shortest ways

of reaching each other), the robots no longer needed such a strong attraction factor

in their decision making process. However, as the robots utilizes the same exploration

algorithm as originally was used by the simple robots, this attractor stopped being an

assisting element, but rather generated the delaying effect described above.

After further investigating this phenomenon, as assumption was made, that by slightly

changing the exploration algorithm, the upgraded robots will easily be able to achieve

superior performance, as originally expected. For example, by simulating noise when

it comes to the locations of the other robots, by deciding randomly whether to take

the mentioned attracting factor into consideration, or by merely changing the averag-

ing vector, decreasing the effect of the robots(v) component on the overall score of a

vertex. However, while the ﬁrst two methods require the robots to be enhanced once

again (as a random generator was not currently included in the robots’ speciﬁcation),

the last cannot easily be analytically shown to improve the performance. Nevertheless,

it is very easy to show that there exist some alternative exploration algorithm which

will enable the upgraded robots to produce far faster exploration than the simple robots

(for example, having a complete knowledge of the graph, each robot can calculate lo-

cally the fastest way in which the entire group can scan the graph, and then simply act

its role in this plan). However, as this was already known prior to this experiment, it

does not contradict the experiment’s result, namely — that enhancing the capabilities

of robots which act according to an algorithm who did not take into consideration this

enhancement, may result in an overall decrease of the system’s performance.

4 Conclusions

This work discussed a multi-robotic system designed for the task of physically ex-

ploring an unknown graph. The problem and the solution model were presented, as

well as the initial results of a selected exploration algorithm. Then, two changes in the

robots’ technical speciﬁcation, intended to increase the robots’ efﬁciency and perfor-

mance were presented, and the results obtained by a group comprising the new robots

were presented and analyzed. These results hinted that counterintuitively, increasing

the robots’ physical capabilities caused a decrease in the system’s overall performance,

due to the appearance of a strong synchronicity between the robots. An estimation was

made concerning a possible solution to this problem, which in turn would have re-

quired both changing the robots’ exploration algorithm and possibly, enhancing even

more the robots’ speciﬁcation. An observation concerning the results of this experi-

ment was made, stating that when “improving” existing robots, one should take extra

care to verify that this improvement does not result in such malicious impacts on the

entire robots group. In conclusion, it is important to state that the results of the experi-

ment discussed in this work do not intend to speak against the enhancements of existing

robots’, or multi-robotic systems’ capabilities per-se, but rather — to remind designers

of such systems that although innocent, any change in original designs should be done

with care and systematic examination (both theoretical and empirical) of the possible

results of such a change.

References

1. S. Hettiarachchi, W. Spears: “Moving swarm formations through obstacle ﬁelds”, in Interna-

tional Conference on Artiﬁcial Intelligence, (2005).

2. I.A. Wagner, A.M. Bruckstein: “From Ants to A(ge)nts: A Special Issue on Ant—Robotics”,

Annals of Mathematics and Artiﬁcial Intelligence, Special Issue on Ant Robotics, Kluer

Academic Publishers, vol. 31, Nos. 1–4, pp. 1–6, (2001)

3. L.Steels: “Cooperation Between Distributed Agents Through Self-Organization”, Decentral-

ized A.I - Proc. ﬁrst European Workshop on Modeling Autonomous Agents in Multi-Agents

world, Y.DeMazeau, J.P.Muller (Eds.), pp. 175–196, Elsevier, (1990)

4. R.C.Arkin: “Integrating Behavioral, Perceptual, and World Knowledge in Reactive Naviga-

tion”, Robotics and Autonomous Systems, 6:pp.105-122, (1990).

5. M.J.Mataric: “Designing Emergent Behaviors: From Local Interactions to Collective Intel-

ligence”, In J.Meyer, H.Roitblat, and S.Wilson, editors, Proceedings of the Second Interna-

tional Conference on Simulation of Adaptive Behavior, pp.432-441, Honolulu, Hawaii, MIT

Press, (1992).

6. T.Haynes, S.Sen: “Evolving Behavioral Strategies in Predators and Prey”, In Gerard Weiss

and Sandip Sen, editors, Adaptation and Learning in Multi-Agent Systems, pp.113-126.

Springer, (1986).

7. B.P.Gerkey, M.J.Mataric: “Sold! Market Methods for Multi-Robot Control”, IEEE Transac-

tions on Robotics and Automation, Special Issue on Multi-robot Systems, (2002).

8. G.Rabideau, T.Estlin, T.Chien, A.Barrett: “A Comparison of Coordinated Planning Methods

for Cooperating Rovers”, Proceedings of the American Institute of Aeronautics and Astro-

nautics (AIAA) Space Technology Conference, (1999).

9. S.M.Thayer, M.B.Dias, B.L.Digney, A.Stentz, B.Nabbe, M.Hebert: “Distributed Robotic

Mapping of Extreme Environments”, Proceedings of SPIE, Vol. 4195, Mobile Robots XV

and Telemanipulator and Telepresence Technologies VII, (2000).

10. M.P.Wellman, P.R.Wurman: “Market-Aware Agents for a Multiagent World”, Robotics and

Autonomous Systems, Vol. 24, pp.115–125, (1998).

11. D.Chevallier, S.Payandeh: “On Kinematic Geometry of Multi-Agent Manipulating System

Based on the Contact Force Information”, The 6

International Conference on Intelligent

Autonomous Systems (IAS-6), pp.188–195, (2000).

12. R.Alami, S.Fleury, M.Herrb, F.Ingrand, F.Robert: “Multi-Robot Cooperation in the Martha

Project”, IEEE Robotics and Automation Magazine, (1997).

13. L.E.Parker: “ALLIANCE: An Architecture for Fault-Tolerant Multi-Robot Cooperation”,

IEEE Transactions on Robotics and Automation, 14(2), pp. 220-240, (1998).

14. M.J.Mataric: “Interaction and Intelligent Behavior”, PhD Thesis, Massachusetts Institute of

Technology, (1994).

15. D.MacKenzie, R.Arkin, J.Cameron: “Multiagent Mission Speciﬁcation and Execution”, Au-

tonomous Robots, 4(1), pp. 29-52, (1997).

16. C.Candea, H.Hu, L.Iocchi, D.Nardi, M.Piaggio: “Coordinating in Multi-Agent RoboCup

Teams”, Robotics and Autonomous Systems, 36(2- 3):67-86, August (2001).

17. A.Yamashita, M.Fukuchi, J.Ota, T.Arai, H.Asama: “Motion Planning for Cooperative Trans-

portation of a Large Object by Multiple Mobile Robots in a 3D Environment”, In Proceedings

of IEEE International Conference on Robotics and Automation, pp. 3144-3151, (2000).

18. S.Premvuti, S.Yuta: “Consideration on the Cooperation of Multiple Autonomous Mobile

Robots”, In Proceedings of the IEEE International Workshop of Intelligent Robots and Sys-

tems, pp. 59-63, Tsuchiura, Japan, (1990).

19. N.Gordon, I.A.Wagner, A.M.Bruckstein: “Discrete Bee Dance Algorithms for Pattern For-

mation on a Grid”, In the proceedings of IEEE International Conference on Intelligent Agent

Technology (IAT03), pp. 545–549, October, (2003).

20. T.Balch, R.Arkin: “Behavior-Based Formation Control for Multi-Robot Teams”, IEEE

Transactions on Robotics and Automation, December (1998).

21. I.M. Rekleitis, G. Dudek, E. Milios: “Experiments in Free-Space Triangulation Using Co-

operative Localization”, IEEE/RSJ/GI International Conference on Intelligent Robots and

Systems (IROS), (2003).

22. I.A. Wagner, A.M. Bruckstein: “Cooperative Cleaners: A Case of Distributed Ant-Robotics”,

“Communications, Computation, Control, and Signal Processing: A Tribute to Thomas

Kailath”, pp. 289–308, Kluwer Academic Publishers, The Netherlands, (1997)

23. Altshuler, Y., Bruckstein, A.M., Wagner, I.A.: “Swarm Robotics for a Dynamic Cleaning

Problem”, in “IEEE Swarm Intelligence Symposium 2005”, pp. 209–216, (2005).

24. Shucker, B., Bennett, J.K.: “Target tracking with distributed robotic macrosensors”, Military

Communications Conference 2005 (MILCOM 2005), vol. 4, pp. 2617–2623, (2005).

25. Y.Altshuler, V. Yanovsky, I.A.Wagner, A.M. Bruckstein: “The Cooperative Hunters - Ef-

ﬁcient Cooperative Search For Smart Targets Using UAV Swarms”, Second International

Conference on Informatics in Control, Automation and Robotics (ICINCO), the First In-

ternational Workshop on Multi-Agent Robotic Systems (MARS), pp. 165–170, Barcelona,

Spain, (2005).

26. Kerr, W., Spears, D.: “Robotic simulation of gases for a surveillance task”, Intelligent Robots

and Systems 2005 (IROS 2005), pp. 2905–2910, (2005).

27. Passino, K., Polycarpou, M., Jacques, D., Pachter, M., Liu, Y., Yang, Y., Flint, M. and Baum,

M.: “Cooperative Control for Autonomous Air Vehicles”, In Cooperative Control and Opti-

mization, R. Murphey and P. Pardalos, editors. Kluwer Academic Publishers, Boston, (2002).

28. Polycarpou, M., Yang, Y. and Passino, K.: “A Cooperative Search Framework for Distributed

Agents”, In Proceedings of the 2001 IEEE International Symposium on Intelligent Control

(Mexico City, Mexico, September 5–7). IEEE, New Jersey, pp. 1–6, (2001).

29. Stone, L.D: “Theory of Optimal Search”, Academic Press, New York, (1975).

30. Koopman, B.O: “The Theory of Search II, Target Detection”, Operations Research 4, 5,

503–531, October, (1956).

31. Vincent, P., Rubin, I.: “A Framework and Analysis for Cooperative Search Using UAV

Swarms”, ACM Simposium on applied computing, (2004).

32. Rekleitisy, I., Lee-Shuey, V., Peng Newz, A., Chosety, H.: “Limited Communication, Multi-

Robot Team Based Coverage”, Proceedings of the 2004 IEEE International Conference on

Robotics and Automation, New Orleans, LA, April, (2004).

33. Koenig, S., Liu, Y.: “Terrain Coverage with Ant Robots: A Simulation Study”, AGENTS’01,

May 28–June 1, Montreal, Quebec, Canada, (2001).

34. I.Rekleitis, A.P New, H.Choset: “Distributed coverage of unknown/unstructured environ-

ments by mobile sensor networks”, the Third MRS workshop, (2005).

35. C.S.Kong, N.A.Peng, I.Rekleitis: “Distributed Coverage with Multi-Robot System”, Pro-

ceedings of the 2006 IEEE International Conference on Robotics and Automation Orlando,

Florida - May (2006).