SIMULATION AND FORMAL VERIFICATION OF REAL TIME
SYSTEMS: A CASE STUDY
Eurico Seabra, José Machado, Jaime Ferreira da Silva
Mechanical Engineering Department, Enginnering School, University of Minho, 4800-058 Guimarães, Portugal
Filomena O. Soares
Industrial Electronics Department, Enginnering School, University of Minho, 4800-058 Guimarães, Portugal
Celina P. Leão
Production System Department, Enginnering School, University of Minho, 4800-057 Braga, Portugal
Keywords: Real Time Systems, Plant Models, Object-Oriented Language, Formal Verification.
Abstract: This paper presents and discusses a case study that applies techniques of simulation together with
techniques of formal verification. A new approach in the plant modelling for formal verification of timed
systems is presented. The modelling of the plant was performed by using the object-oriented language
Modelica with the library for hierarchical state machines StateGraph and the simulation results were used as
input for the formal verification tasks, using the model checker UPPAAL. It is presented, in a more detailed
way, the part of this work that is related to the plant simulation.
1 INTRODUCTION
Modern engineered systems have reached a high
degree of complexity that requires systematic design
methodologies and model-based approaches to
ensure the correct and competitive performance. In
particular, the use of digital controllers has been
proven that small errors in their design may lead to
catastrophic failures.
Recent years have witnessed a significant growth
of interest in the modelling and simulation of
physical systems. A key factor in this growth was
the development of efficient equation-based
simulation languages. Such languages have been
designed to allow automatic generation of efficient
simulation code from declarative specifications. The
Modelica language (Fritzson et al. 1998, Elmqvist et
al. 1999, Fritzson et al. 2002)
and its associated
support technologies have achieved considerable
success through the development of specific
libraries. However, a significant part of the software
development effort is spent on detecting deviations
from specifications and subsequently localizing the
sources of such errors. The high-level of abstraction
of equation-based models presents new challenges to
modelling and simulation tools due to the large gap
between the declarative specification and the
executable machine code. This abstraction gap leads
to difficulties in finding and correcting model
inconsistencies and errors, which are not uncommon
in the process of developing complex physical
system models.
Among the several techniques of industrial
controllers analysis available, Simulation (Baresi et
al. 2000, Baresi et al. 2002) and Formal Verification
(Moon, 1994, Roussel and Denis, 2002), can be
distinguished due to their utility. In the research
works on industrial controller’s analysis, these two
techniques are rarely used simultaneously. If the
Simulation is faster to execute, it presents the
limitation of considering only some system
behaviour evolution scenarios. Formal Verification
presents the advantage of testing all the possible
system behaviour evolution scenarios but,
sometimes, it takes a large amount of time for the
attainment of formal verification results. In this
308
Seabra E., Machado J., Ferreira da Silva J., O. Soares F. and P. Leão C. (2007).
SIMULATION AND FORMAL VERIFICATION OF REAL TIME SYSTEMS: A CASE STUDY.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 308-313
DOI: 10.5220/0001636703080313
Copyright
c
 SciTePress

paper it is shown, as it is possible, and desirable, to
conciliate these two techniques in the analysis of
industrial controllers. With the simultaneous use of
these two techniques, the developed industrial
controllers are more robust and not subject to errors.
Using this approach, the command of those
systems can be simulated and tested when the
physical part of the machine still does not exist. This
way of simulation allows to reduce the production
times of the automation systems because the
manufacture do not need the physical part of the
machine for later perform tests and simulation of the
command of the system. This paper is focused in the
simulation of timed systems.
To accomplish our goals, in this work, the paper
is organized as follows. In Section 1, it is presented
the challenge proposed to achieve in this work.
Section 2 presents a general presentation of the case
study involving a system with two tanks, a heating
device, a mixer device, level control sensors and
valves to control the liquids flow. Further, it is
presented the methodology to obtain the controller
program deduced from an IEC 60848 SFC
specification of the system desired behaviour.
Section 3 is exclusively devoted to the plant
modelling, being presented the adopted approach.
Section 4 presents and discusses the obtained results
on simulation performed with the Modelica
Language. Finally, in Section 5, the main
conclusions and future work are presented.
2 SYSTEM DESCRIPTION
The case study is an adapted version of the
benchmark example presented by (Kowalewski et
al. 2001) and (Huuck et al. 2001) that corresponds to
an evaporator system.
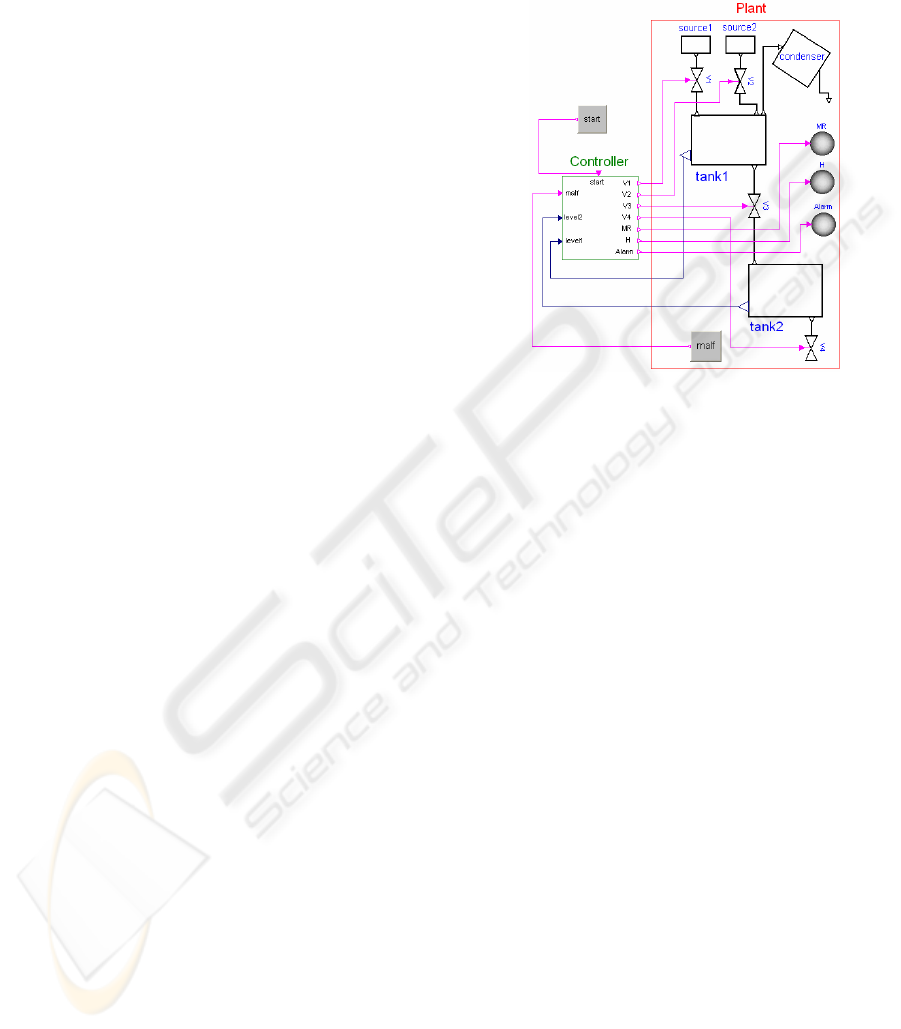
The system (Fig. 1) consists of two tanks, where
tank1 is heated and mixed, one condenser, two level
analogue sensors (one for each tank) and four on-off
valves.
In the normal operation, the system works as
follows. Tank1 is filled with two solutions by
opening valves V1 and V2. When the level becomes
high, the valves are closed and liquids are mixed by
a mixer device for dilution. After two time units, the
heating device is switch on to increase the
temperature of the solution. After 20 time units, the
required concentration has been reached and the
heater is switched off. Meanwhile, during the
heating phase, part of the liquid has been evaporated
and cooled by the condenser. The remaining part is
drained in tank2 by opening the valve V3. When the
first tank is empty, the mixer is stopped and the
solution in tank2 stays for post-processing step, to
stay liquid, for 32 time units. At that point, the valve
V4 is opened to empty tank2.
Figure 1: Scheme of the evaporator system.
Throughout normal operation mode, the system
may malfunction. During evaporation, the condenser
may fail: the steam can not be cooled and the
pressure inside the condenser rises. Therefore, the
heater must be switched off to avoid the condenser
explosion. By doing so, the temperature of tank1
decreases and the solution may become solid and
can not be drained in tank2. Hence, valve V3 must
be opened early enough for preventing tank2
overflow, but after opening first valve V4.
In the case of a condenser malfunction, it is also
necessary to ensure that some response times of the
control program, taking into account the timing
characteristics of the physical devices:
- whenever a condenser malfunction starts, the
condenser can explode if steam is produced
during 22 time units;
- if the heating device is switched off, the
steam production stops after 12 time units;
- if no steam is produced in tank 1, the solution
may solidify after 19 time units;
- emptying tank 2 takes between 0 and 26 time
units;
- filling tank 1 takes 6 time units, at most.
2.1 Controller
In order to guarantee the desired behaviour of the
evaporator system described above, the controller
was developed according to IEC 60848 SFC
specification, which is presented in Figure 2.
SIMULATION AND FORMAL VERIFICATION OF REAL TIME SYSTEMS: A CASE STUDY
309

The PLC program which controls the process in
closed-loop has input and output variables as
described in Table1.
Table 1: Input/Output variables of the controller.
Input
Output
start – process start
level1 – % fill tank1
level2 – % fill tank2
malf – condenser
malfunction
V1 – open valve1
V2 – open valve2
V3 – open valve3
V4 – open valve4
H – switch Heater on
MR – switch Mixer on
Alarm – start alarm
The tank level is given in % of the fill tank. In this
research work, the Boolean variables T1F (tank1
full) and T2F (tank2 full) were considered true when
the level1 and level2 was greater than 0.98,
respectively. On the other hand, the Boolean
expression T1E (tank1 empty) and T2E (tank2
empty) were assumed true when the level1 and
level2 was less than 0.01, respectively.
Figure 2: SFC of the system controller.
3 PLANT MODEL
The plant modelling was carried out in two steps.
First, the plant was modelled using the Dymola
program and the object-oriented language Modelica
(Elmqvist and Mattson, 1997) with the library for
hierarchical state machines StateGraph (Otter,
2005). Subsequently, the obtained models were used
as a base to develop the UPPAAL (David et al.
2003) models that are used on formal verification
tasks.
It should be highlighted that the most important
data obtained by the Modelica simulation considered
on the formal verification tasks is the set of
simulation functioning delays. These delays are used
to define the time units used on the UPPAAL
modules of the plant model (Machado et al. 2007).
As the main aim of this paper deals with the
plant simulation by using Modelica Language, it is
only presented the modelling of tank1 by UPPAAL.
3.1 Tank1
The tank1 model is first simulated by using the
Dymola software with the Modelica program code
presented in the Figure 3. The obtained times from
the simulation were used on formal verification with
UPPAAL.
Figure 3: Modelica program code for the model of tank1.
Figure 4 shows the corresponding model of the
tank1 developed by UPPAAL for formal verification
purposes.
Figure 4: UPPAAL model of the tank1.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
310

3.2 Tank2
The Modelica program code for modelling the
tank2, presented in Figure 5, is similar to the code
obtained for the tank1 model. The main difference
between these two codes is due to the tanks have
different numbers of fill sources. The tank 1 has two
fill sources while the tank 2 has one only.
Figure 5: Modelica program code for the model of tank2.
4 SIMULATION RESULTS
In order to perform the simulation, it is necessary to
define the parameters, start and stop time of the
simulation, the interval output length or number of
output intervals and the integration algorithm. In the
present work, in all simulations performed, the Dass
algorithm (Basu, 2006) with 500 output intervals
was used.
In order to study the system behaviour different
values for physical variables of the plant were used.
Table 2 shows the variables considered in the
simulation of the plant model.
Table 2: Variables of the plant.
Plant Variable
source1, source 2 Q1, Q2 - flow rate [m
3
/s]
tank1, tank2
G1, G2 – ground area [m
2
]
Ht1, Ht2 –height [m]
A1, A2 – drain hole area [m
2
]
The first two simulation performed were devoted
to verify if the SFC of the controller system (Fig.2)
modelled with Modelica language with the library
for hierarchical state machines StateGraph simulated
correctly the evaporator system, respectively, in
their normal and malfunction operation. The values
for the plant variables considered in these
simulations were Q1=1, Q2=0.5, G1=G2=1,
Ht1=Ht2=1, A1=0.2 and A2=0.05.
Figures 6 and 7 show results of the simulation
without the occurrence of the condenser malfunction
during the production cycle, which corresponds to
the normal operation, respectively, for the level
tanks and for the controller outputs.
Observing Figures 6 and 7 it can be concluded
that the system is properly simulated by the
developed program, since during the time specified
by the SFC the tanks remain filled and empty, as
well as, the switch logical state of the controller
outputs.
On the other hand, Figures 8 and 9 show results
of the simulation with the occurrence of the
condenser malfunction during the production cycle,
which corresponds to the malfunction operation. The
malfunction occurred in a random way 15s after the
start of the plant functioning.
Analysing Figures 8 and 9 it can be also
concluded that the malfunction operation is properly
simulated by the proposed program. Because it can
be verified, taking into account the Figure 8, that at
the malfunction occurrence (time 15s) the solution
present in the tank1 is immediately drained for the
tank2 and later emptied. In the same way, analysing
the Figure 9, it can be verified that at the time 15s
occur simultaneous the switch off the mixer and the
heater and the alarm switch on, which corresponds
to the SFC specification of the controller.
0 10 20 30 40 50 60 70
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Fill tank [%]
Time [s]
level tank1 level tank2
Figure 6: Level tanks in function of time in normal
operation of the evaporator system.
SIMULATION AND FORMAL VERIFICATION OF REAL TIME SYSTEMS: A CASE STUDY
311

0 10 20 30 40 50 60 70
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Time [s]
MR H
A
larm
Figure 7: Switch state of the mixer, heater and alarm in
normal operation of the evaporator system.
0 10 20 30 40 50 60 70
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Fill tank [%]
Time [s]
level tank1 level tank2
Figure 8: Level tanks in function of time with occurrence
of condenser malfunction (time = 15s).
0 10 20 30 40 50 60 70
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Time [s]
MR H
A
larm
Figure 9: Switch state of the mixer, heater and alarm with
occurrence of condenser malfunction (time =15s).
It becomes still necessary, in addition to the
verification that the modelling of the system obey to
the SFC of the system controller, to guarantee that in
the case of condenser malfunction don’t occur
solidification or explosion of the solution in the
tanks. Thus it is necessary taking into account the
timing characteristics of the physical devices.
For example, the simulation presented in Figures
8 and 9, which values for the plant variables
considered were Q1=1, Q2=0.5, G1=G2=1,
Ht1=Ht2=1, A1=0.2 and A2=0.05, the obtained
times for fill and empty the tank1 were, respectively,
0.6533s (limit 6s) and 2,1255s (limit 19s) and for the
tank 2 respectively for fill and empty were 2,2655s
(similar to the time of empty tank1) and 8,4361s
(limit 26s). This simulation allowed to show that
with these values of plant variables the system
doesn't have serious functioning anomalies that can
put in risk humans lives and material goods.
In order to obtain the relation between the plant
variables and the time of the critical operations,
some simulations were performed using several
values of plant variables. Figure 10 and 11 show
results of these simulations, respectively related to
the empty tanks time (equal for the tank1 and tank2)
and fill tank1 time, which correspond at the times of
the critical operations of the evaporator system.
0
20
40
60
80
100
120
140
160
0 0.05 0.1 0.15 0.2 0.25
Drain hole area [m2]
Empty tank time [s]
G*Ht=1
G*Ht=2
G*Ht=3
G*Ht=4
Figure 10: Empty tank time in function of plant variables.
0
5
10
15
20
25
30
024681012141
6
G1*Ht1 [m3]
Fill tank1 time [s]
Q1+Q2=0,5
Q1+Q2=1
Q1+Q2=1,5
Q1+Q2=2
Figure 11: Fill tank1 time in function of plant variables.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
312

5 CONCLUSIONS
The simulation used to evaluate the plant behaviour
has been developed and proposed in this paper.
The results obtained suggested that this approach
is adequate to obtain the relation between the plant
variables involved in the evaporator system. The
present research proved to be successful using the
Modelica programming Language to obtain plant
models and to get functioning delays in which a
property can, or not, be proved using techniques of
formal verification. Moreover, the simulation
techniques allow us to test different delays of the
plant functioning and to see if a property, for
different considered delays, is still true or if different
delays imply that a property is true and after is false.
For the analysis of a system controller program it
is desirable the use of simulation before using
formal verification. With the simulation it is possible
to eliminate a set of program errors of some possible
system behaviours in reduced intervals of time. This
would not happen, in most of the cases, if these
errors were detected only through the use of formal
verification techniques. Conciliating these two
techniques the time necessary for the attainment of
results through the use of the formal verification
technique can be substantially reduced. With this
approach a manufacturer of industrial automated
systems does not need the physical part of the
machine for later perform tests and simulation of the
system controller. In consequence, they allow,
together, to reduce the times of production of the
automated systems.
ACKNOWLEDGEMENTS
This research project is carried out in the context of
the SCAPS Project supported by FCT, the
Portuguese Foundation for Science and Technology,
and FEDER, the European regional development
fund, under contract POCI/EME/61425/2004 that
deals with safety control of automated production
systems.
REFERENCES
Baresi L., Mauri M., Monti A., Pezzè M., 2000.
PLCTOOLS: Design, Formal Validation, and Code
Generation for Programmable Controllers. Special
Session at IEEE Conference on Systems, Man, and
Cybernetics. Nashville USA.
Baresi L., Mauri M., Pezzè M., 2002. PLCTools: Graph
Transformation Meets PLC Design. Electronic Notes
in Theoretical Computer Science 72 No. 2.
Basu S., Pollack R., Roy M., 2006. Algorithms in Real
Algebraic Geometry - Algorithms and Computation in
Mathematics. Springer Editions, vol. 10, 2ªedition.
David A., Behrmann G., Larsen K. G., Yi W., 2003. A
Tool Architecture for the Next Generation of
UPPAAL. Technical Report n. 2003-011, Department
of Information Technology, Uppsala University, Feb.
20 pages.
Elmqvist E., Mattson S., 1997. An Introduction to the
Physical Modelling Language Modelica. Proceedings
of the 9th European Simulation Symposium, ESS'97.
Passau, Germany.
Elmqvist, Hilding, Mattsson S., Otter M., 1999. Modelica
- a language for physical system modeling,
visualization and interaction. Proceedings of the IEEE
Symposium on Computer-Aided Control System
Design. August, Hawaii.
Fritzson, Peter, Vadim E., 1998. Modelica, a general
object-oriented language for continuous and
discrete-event system modeling and simulation, 12th
European Conference on Object-Oriented
Programming (ECOOP’98). Brussels, Belgium.
Fritzson, Peter, Bunus P., 2002. Modelica, a general
object-oriented language for continuous and
discrete-event system modelling and simulation.
Proceedings of the 35th Annual Simulation
Symposium. April, San Diego, CA.
Huuck R., Lukoschus B., Lakhnech. Y., 2001. Verifying
Untimed and Timed Aspects of the Experimental Batch
Plant. European Journal of Control, vol. 7, nº 4, pp.
400-415.
Kowalewski S., Stursberg O., Bauer. N., 2001. An
Experimental Batch Plant as a Test Case for the
Verication of Hybrid Systems. European Journal of
Control.
Machado J., Seabra E., Soares F., Campos J., 2007. A new
Plant Modelling Approach for Formal Verification
Purposes. Submitted at 11
th
IFAC/IFORS/IMACS/
IFIP Symposium on Large Scale Systems: Theory and
Applications. Gdansk, Poland.
Moon I. 1994. Modeling programmable logic controllers
for logic verification. IEEE Control Systems, 14, 2,
pp. 53-59.
Otter M., Årzén K., Dressler I., 2005 StateGraph - A
Modelica Library for Hierarchical State Machines.
Modelica 2005 Proceedings.
Roussel M., Denis B., 2002. Safety properties verification
of ladder diagram programs. Journal Européen des
Systèmes Automatisés, vol. 36, pp. 905-917.
SIMULATION AND FORMAL VERIFICATION OF REAL TIME SYSTEMS: A CASE STUDY
313