
MODELING AND CONTROL OF AN EXPERIMENTAL SWITCHED
MANUFACTURING SYSTEM
Michael Canu, Dominique Morel and Naly Rakoto-Ravalontsalama*
Ecole des Mines de Nantes (*and IRCCyN)
4 rue Alfred Kastler, 44307 Nantes Cedex 03, France
Keywords:
Manufacturing Systems.
Abstract:
The notion of switched discrete event systems (DES) has been introduced recently. This is a class of DES
where each automaton is the composition of two basic automata, but with different composition operators.
A switching occurs when there is a change of the composition operator, but keeping the same two basic au-
tomata. A mode behavior is defined as the active DES behavior for a given composition operator. Composition
operators are supposed to change more than once so that each mode is visited more than once. In this paper
we study the modeling and control of an experimental manufacturing system as an example of switched DES.
1 INTRODUCTION
Supervisory control initiated by Ramadge and Won-
ham (Ramadge and Wonham, 1987) provides a sys-
tematic approach for the control of discrete event sys-
tem (DES) plant. Most of the properties of a given
composed system depend on the composition oper-
ator. The modular approach reflects the underlying
physical properties of complex systems such as man-
ufacturing systems.
The most common composition operators used in
supervisory control theory are the product and the par-
allel composition (Cassandras and Lafortune, 1999),
(Wonham, 2004). However many different types of
composition operators have been defined, e.g., the pri-
oritized synchronous composition (0), the biased syn-
chronous composition (Lafortune and Chen, 1990),
see (Wenck and Richter, 2004) for a review of most
of the composition operators. Multi-Agent composi-
tion operator (Romanovski and Caines, 2002), (Ro-
manovski and Caines, 2006) is another kind of opera-
tor, which differs from the synchronous product in the
aspects of simultaneity and synchronization.
Related work concerns a) fault diagnosis for DES
(the readers are referred to (Jensen, 2003) for a com-
prehensive survey), b) mode-automata for reactive
system programming, introduced in (Maraninchi and
Remond, 1998), c) supervisory uniqueness for oper-
ating mode systems studied in (Kamach et al., 2005)
where the authors propose a multi-model approach to
DES, and finally d) sensor failure tolerant supervisory
control proposed in (Rohloff, 2005) where different
automata are used to model the system observation
behavior in the various modes of operations.
This paper studies the application of switched
DES methodology to an Experimental Manufacturing
Cell. This cell is composed of two robotized work-
stations connected to a central conveyor belt. Re-
cently, three new semi-automated workstations have
been added in order to increase the flexibility aspects
of the cell. This flexibility allows the designer to
study different mode behaviors of the experimental
cell.
The paper is organized as follows. In Section 2,
the notation and preliminaries are given. The notion
of switched DES is recalled in Section 3. In Section
4, the controllability property is studied. Finally the
experimental cell behavior is described in Section 5.
484
Canu M., Morel D. and Rakoto-Ravalontsalama N. (2007).
MODELING AND CONTROL OF AN EXPERIMENTAL SWITCHED MANUFACTURING SYSTEM.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 484-488
DOI: 10.5220/0001637204840488
Copyright
c
SciTePress
2 NOTATION AND
PRELIMINARIES
Let the discrete event system plant be modeled by a
finite state automaton (Hopcroft and Ullman, 1979)
G = (Q, Σ, δ, q
0
, Q
m
)
where Q is the finite set of states, Σ is the finite set
of events associated with the transitions in G, δ : Q×
Σ → Q is the partial transition function, q
0
is the initial
state and Q
m
⊆ Q is the set of marked states.
Let Σ
∗
be the set of all finite strings of elements in
Σ including the empty string ε. The function δ can be
generalized to δ : Σ
∗
× Q → Q. The notation δ(s, q)!
for any s ∈ Σ
∗
and q ∈ Q denotes that δ(s, q) is defined.
Let L(G) ⊆ Σ
∗
be the language generated by G, that
is,
L(G) = {s ∈ Σ
∗
|δ(s, q
0
)!}
Let K ⊆ Σ
∗
be a language. The set of all prefixes of
strings in K is denoted by
K with K = {s ∈ Σ
∗
|∃ t ∈
Σ
∗
;st ∈ K}. A language K is said to be prefix closed
if K = K. The event set Σ is decomposed into two
subsets Σ
c
and Σ
uc
of controllable and uncontrollable
events, respectively, where Σ
c
∩Σ
uc
=
/
0. A controller,
called a supervisor, controls the plant by dynamically
disabling some of the controllable events. A closed
language K ⊆ L(G) is said to be controllable with re-
spect to L(G) and Σ
uc
if (Ramadge, 1987)
KΣ
uc
∩ L(G) ⊆ K.
In the supervisory control theory, composition
means synchronization of finite state automata. The
basis for the definition of all the composition op-
erators are G
a
= (Q
a
, Σ
a
, δ
a
, q
0a
, Q
ma
) and G
b
=
(Q
b
, Σ
b
, δ
b
, q
0b
, Q
mb
) with disjoint state sets Q
a
∩
Q
b
=
/
0 but generally overlapping event sets. The
result of any composition is an automaton G
i
=
G
a
||
op
i
G
b
= (Q, Σ, δ, q
0
, Q
m
) with the state Q = Q
a
×
Q
b
, the event set Σ = Σ
a
∪ Σ
b
and initial state x
0
=
x
0a
, x
0b
, where op
i
is a composition operator. Each
operator is defined by a distinct transition function
with σ ∈ Σ a single event and q ∈ Q a state.
Among the different types of composition opera-
tors, we recall here the biased synchronous composi-
tion (BSC) and the strict product composition (SPC).
Definition 1 (Lafortune and Chen, 1990) The Bi-
ased Synchronous Composition (BSC) is defined as
follows. The automaton G
a
is called the master and
G
b
is called the follower.
δ(q, σ) =
δ
a
(q
a
, σ) × δ
b
(q
b
, σ) if δ
a
(q
a
, σ)!∧ δ
b
(q
b
, σ)!
δ
a
(q
a
, σ) × {q
b
} if δ
a
(q
a
, σ)!∧ ¬δ
b
(q
b
, σ)!
/
0 otherwise.
Definition 2 The strict product composition (SPC)
is defined as follows.
δ(q, σ) =
δ
a
(q
a
, σ) × δ
b
(q
b
, σ) if δ
a
(q
a
, σ)!∧ δ
b
(q
b
, σ)!
/
0 otherwise.
These two composition operators will be taken as
example in the next sections.
3 SWITCHED DES
The basic idea is the following. Without loss of gen-
erality we consider two automata G
a
and G
b
as de-
fined above. Let G
i
be the composed automaton from
G
a
and G
b
with operator op
i
, that is G
i
= G
a
||
op
i
G
b
.
In the same way let G
j
be the composed automaton
from the same G
a
and G
b
but with operator op
j
, that
is G
j
= G
a
||
op
j
G
b
, as it is depicted in Figure 2 and
Figure 3.
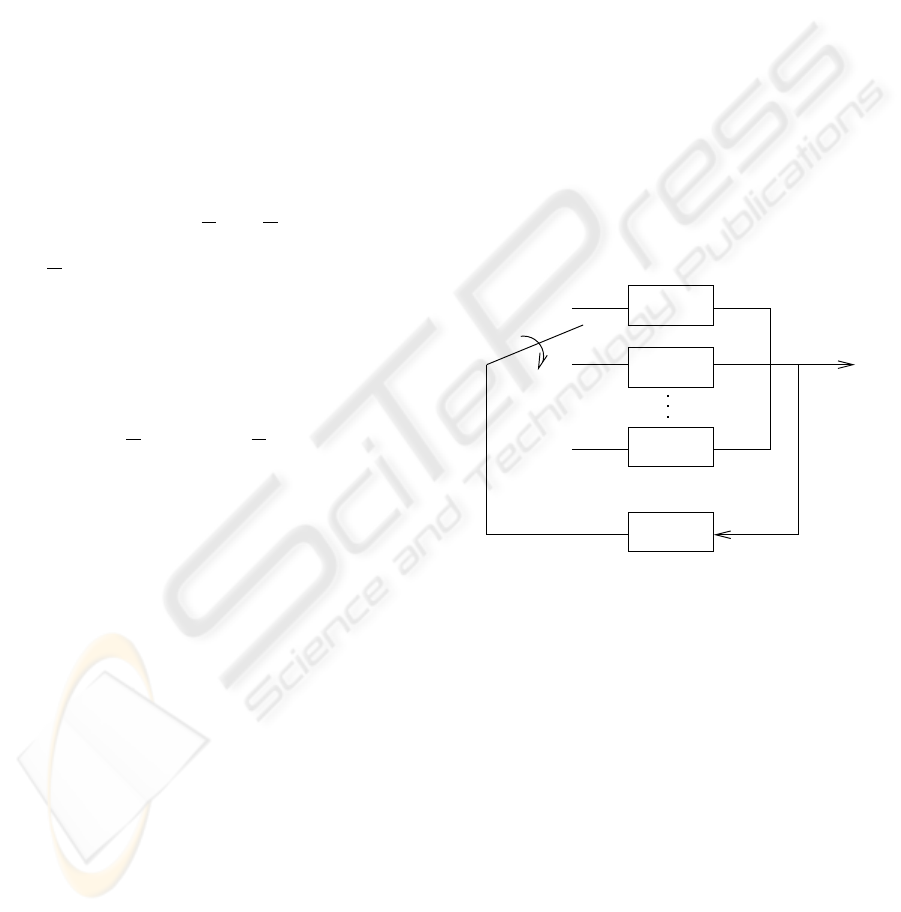
DES 1
DES 2
DES n
switch
Supervisor
Figure 1: Switched DES.
Definition 3 Equivalent states.
The states (q
a
, q
b
)
i
of automaton G
i
and (q
c
, q
d
)
j
of
automaton G
j
are said to be equivalent (q
a
, q
b
)
i
≡
(q
c
, q
d
)
j
if they result from the composition of the
same pair of states but with different composition op-
erators (q
a
= q
c
and q
b
= q
d
).
Assumptions. Given two automata G
i
and G
j
,
switching between automaton G
i
and automaton G
j
is possible if the following assumptions hold.
1. G
i
and G
j
have at least two equivalent states
2. Switching between G
i
and G
j
is performed
through their equivalent states.
3. Switching from G
i
to G
j
has zero duration, as well
as from G
j
to G
i
.
MODELING AND CONTROL OF AN EXPERIMENTAL SWITCHED MANUFACTURING SYSTEM
485
Definition 4 (Rakoto, 2006b) Switched DES.
A switched discrete event system is defined as fol-
lows.
L
switched
(G) = L(G
i
), i ∈ I = {1, . . . , n} (1)
where G
i
is the model of DES
i
, and I is an index set.
In this special case, G
i
= G
a
||
op
i
G
b
.
We can see in Figure 2 and Figure 3 the automa-
ton G
1
and G
2
, respectively. Then automata G
1
and
G
2
can switch between them, as it is shown in Fig-
ure 4. Actually, the switching are made through the
equivalent states of G
1
and G
2
, see Figure 5.
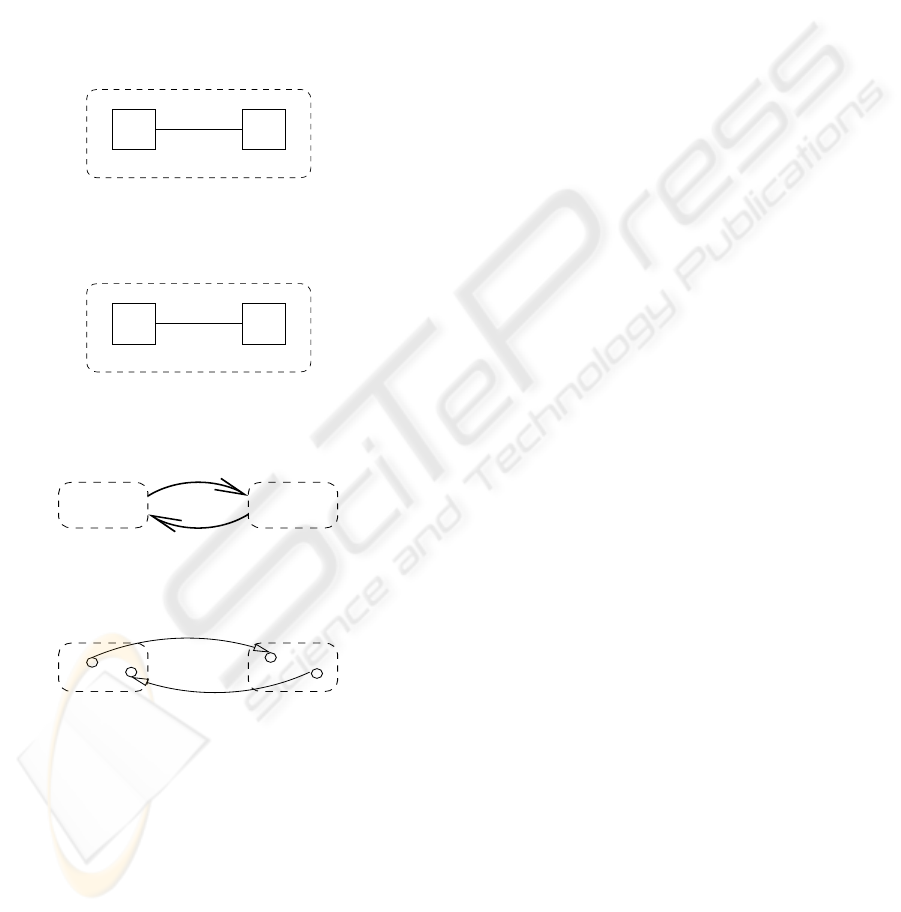
G1 = Ga ||_op1 Gb
Ga Gb
Figure 2: Automaton G
1
.
Ga Gb
G2 = Ga ||_op2 Gb
Figure 3: Automaton G
2
.
G1 G2
Figure 4: Switched automaton.
G1
G2
Figure 5: Automata switching through equivalent states.
We give here below some examples of switched
DES:
• Manufacturing systems where the operating
modes are changing (e.g. from normal mode to
degenerated mode)
• Discrete event systems after an emergency signal
(from normal to safety mode)
• Complex systems changing from normal mode to
recovery mode (or from safety mode to normal
mode).
We can distinguish, like for the switched
continuous-time systems, the notion of autonomous
switching where no external action is performed and
the notion of controlled switching, where the switch-
ing is forced. The notion of switched DES has been
adapted from the switched continuous-time systems.
For a survey of switched continuous-time systems,
one can refer to (Liberzon and Morse, 1999) and the
references therein.
On one hand DES and continuous-time systems
share the notion of controllability (but each domain
has its own definition). On the other hand, stabil-
ity analysis in continuous-time systems cannot be
adapted to DES (even though some work exist on the
stability of DES (Passino et al., 1994), (Passino and
Burgess, 1998) and the references therein). Thus the
notion of stability analysis has been changed to non-
blocking analysis. Before defining the problems, we
need to define the notion of switching sequence. A
switching sequence is defined to be the successive
active automata when the successive switchings oc-
cur. The following problems have been defined in
(Rakoto, 2006b)
• Problem A. Find conditions that guarantee that the
switched DES (1) is controllable with respect to
the Language L(G) and with respect to all the un-
controllable events, for any switching sequence.
• Problem B. Identify the classes of switching se-
quences for which the switched DES (1) is con-
trollable with respect to the Language L(G) and
with respect to all the uncontrollable events.
• Problem C. Find conditions that guarantee that the
switched DES (1) is nonblocking.
• Problem D. Identify the classes of switching se-
quences for which the switched DES (1) is non-
blocking.
We can note that discretization of a switched continu-
ous system (see e.g., (Rakoto, 2001) may be a solution
to the adaptation to the DES context.
4 CONTROLLABILITY OF
SWITCHED DES
In this section we address a specific problem related
to the controllability of a switched DES (1).
Problem 1. Given a switched automaton
L
switched
= L(G) = L(G
i
), i ∈ I = {1, 2} where
G
1
= G
a
||
op
1
G
b
= G
a
||
BSC
G
b
and G
2
= G
a
||
op
2
G
b
=
G
a
||
SPC
G
b
, find the conditions that guarantee the con-
trollability of the switched DES L
switched
= L(G).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
486
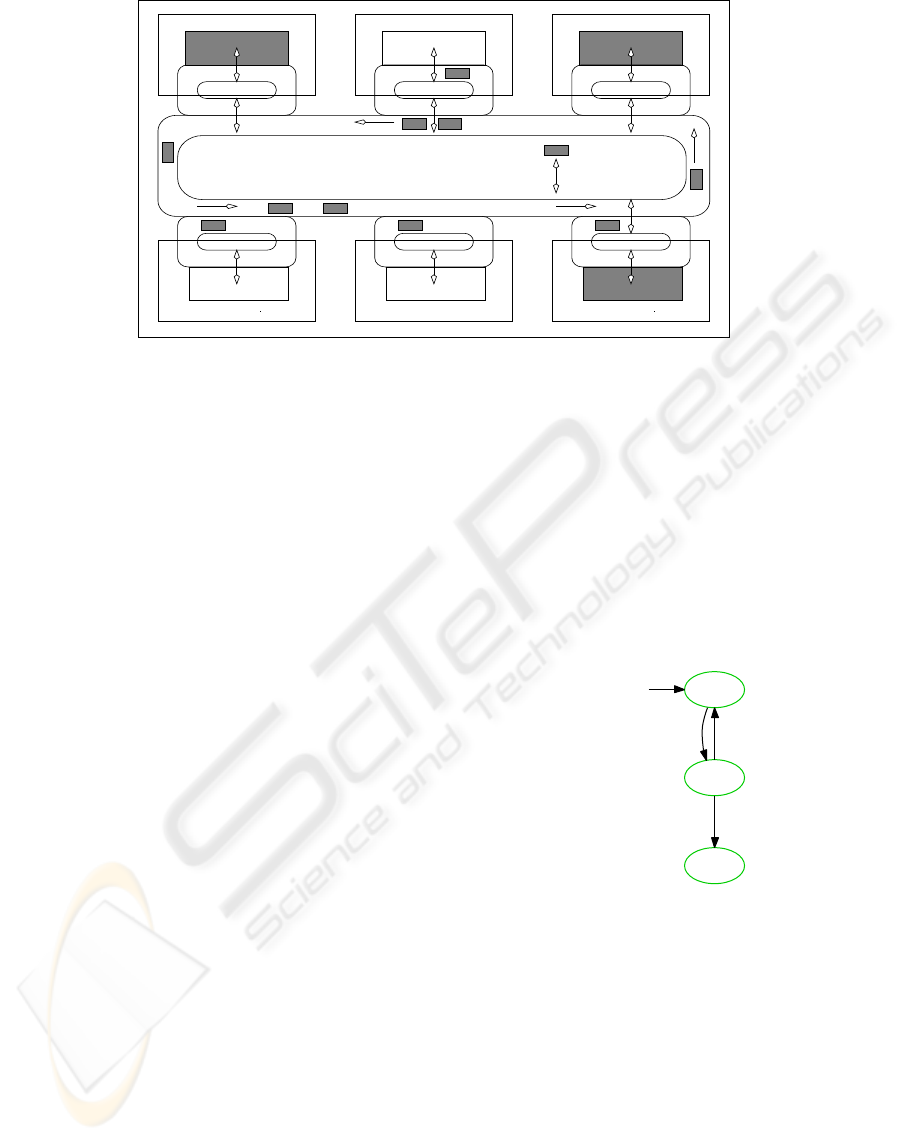
ws5_conveyor
Robot_2
Robot_9 Robot_1
ws1_conveyor
ws3_conveyor ws2_conveyor ws4_conveyor
EMN Experimental Manufacturing Cell
(Assembly of DUPLO blocks)
Workstation_1Load-Unload_Station
Central Conveyor Belt (CCB)
semi-automated
Workstation_3
Pallet
Transfer System
Workstation_2
Workstation_4
semi-automated
Workstation_5
semi-automated
Figure 6: Experimental Manufacturing Cell.
Theorem 1 Given a switched automaton L
switched
=
L(G) = L(G
i
), i ∈ I = {1, 2} where G
1
= G
a
||
BSC
G
b
and G
2
= G
a
||
SPC
G
b
, the switched automaton L(G) =
L(G
i
) is controllable with respect to both L(G
1
) and
L(G
2
) and with respect to Σ
u
c if
1. K
a
, K
b
, L(G
2
) are pairwise non conflicting
2. K
b
, L(G
a
) are non conflicting
3. K
b
is controllable w.r.t. L(G
a
)
Proof. The proof can be found in (Rakoto, 2006b). It
is based on four propositions that have been given in
(Wenck and Richter, 2004).
5 EXPERIMENTAL
MANUFACTURING CELL
An automated manufacturing system generally con-
sists of a number of interconnected material process-
ing stations capable of processing a wide variety of
part types, a material transport system, a communica-
tion system for integrating all aspects of manufactur-
ing and a supervisory control system. The experimen-
tal manufacturing cell is composed of the following
components (Chen et al., 2004): a) a central conveyor
belt, b) two robotized workstations, with a station
conveyor each, c) a transfer system between the cen-
tral conveyor belt and the station conveyor, d) another
transfer system between the station conveyor and the
corresponding robot, and e) a load-unload robotized
worksation.
Recently, three semi-automated workstations have
been added to increase the flexibility aspects of the
cell. Indeed, each semi-automated workstation can
perform either manual or automated tasks. The ex-
perimental manufacturing cell is depicted in Figure 6.
Behavioral specifications of such an automated
manufacturing system include: a) logic-based spec-
ifications (e.g. safety, error recovery, the sequenc-
ing of operations, part routing and production vol-
ume requirement), b) temporal production specifica-
tion: production times, and c) utility optimality spec-
ification: e.g. costs.
S0.S0
S1.S1
a g
S2.S0
!b
Figure 7: Composed Automaton.
The results were obtained using the tool Suprem-
ica (Akesson et al, 2006). Only two types of composi-
tion product were used. However this can be extended
to different types of composition products.
6 CONCLUSIONS
This paper studies the application of the switched
DES methodology, introduced previously to an Ex-
perimental Manufacturing Cell. The different mode
behaviors were possible to obtain thanks to the re-
MODELING AND CONTROL OF AN EXPERIMENTAL SWITCHED MANUFACTURING SYSTEM
487

S0.S0.S0
S1.S1.S1
a
S0.S1.S0
aS0.S2.S0
S1.S2.S1
a
g
!b
S2.S1.S2
d
!b
g
S2.S2.S2
d
r
r
Figure 8: Composed Automaton (with priority).
cently added semi-automated workstations. These
latter increased the flexibility of the system, and it
allows the designer to apply the switched DES ap-
proach. Future work will be focused on a) obtain-
ing more different mode behaviors for controllability,
and b) study nonblocking properties in some specific
cases.
ACKNOWLEDGEMENTS
This work was supported in part by the French
2000-2006 ”Contrat Etat-R
´
egion CER STIC 9, N.
18036: Optimisation des processus industriels”
Nantes, France.
REFERENCES
K. Akesson, M. Fabian, H. Flordal, and R. Malik. ”Suprem-
ica - An integrated environment for verification, syn-
thesis and simulation of discrete event systems,”
Proc. of 2006 Workshop of Discrete Event Sys-
tems (WODES’06), July 2006, Ann Arbor, Michigan,
USA.
C.G. Cassandras and S. Lafortune. Introduction to Discrete
Event Systems. Boston, MA, USA: Kluwer Academic
Publishers, 1999.
X. Chen, D. Morel, and N. Rakoto-Ravalontsalama ”Multi-
Agent Based Supervisory Control of an Experimental
Manufacturing Cell”. Proc. of IFAC Symposium on
Large Scale Systems (LSS 2004) Osaka, Japan, July
26-28, 2004, pp. 391–394.
M. Heymann. ”Concurrency and discrete event control,”
In IEEE Control Systems Magazine, Vol. 10 N.4, pp.
103–112, 1990.
R.M. Jensen. ”DES Controller Synthesis and Fault Toler-
ant Control: A Survey of recent advances,” Technical
report TR-2003-40, Th IT University of Copenhagen,
Denmark, 2003.
J.E. Hopcroft and J.D. Ullman, ”Introduction to Automata
Theory, Languages, and Computation,” Addison-
Wesley, Reading, MA, USA, 1979.
O. Kamach, L. Pietrac, and E. Niel. ”Supervisory unique-
ness for operating mode systems,” Proc. of World
IFAC Congress 2005, Prague, Czech Republic, July
2005.
S. Lafortune and E. Chen. ”The infimal closed controllable
superlanguage and its application in supervisory con-
trol,” In IEEE Trans. on Automatic Control, vol.35,
N.4 pp. 398–405, 1990.
D. Liberzon and A.S. Morse. ”Basic problems in stability
and design of switched systems,” In IEEE Control
Systems Magazine, pp. 59–70, Oct. 1999.
F. Maraninchi and Y. Remond. ”Mode-Automata: About
modes and states for reactive systems” Proc. of Euro-
pean Symp. on Programming 1998, Lisbon, Portugal,
1998.
K.M. Passino, A.N. Michel, and P.J. Antsaklis. ”Lyapunov
stability of a class of discrete event systems,” In IEEE
Trans. on Automatic Control, vol.39, N.2 pp. 269–
279, Feb 1994.
K.M. Passino and K.L. Burgess. ”Stability Analysis of Dis-
crete Event Systems,” Wiley, New York, USA, 1998.
N. Rakoto-Ravalontsalama. ”Discrete approximation of
continuous and hybrid systems: Some consequences
to supervisory control,” Proc. of IFAC SSC 2001
(Symp. on System Structure and Control), Paper N.
123, Prague, Czech Republic, Aug. 2001.
N. Rakoto-Ravalontsalama. ”Supervisory control of
switched discrete event systems,” Proc. of Int. Sympo-
sium on MTNS 2006, July 24-28, 2006, Kyoto, Japan.
P.J. Ramadge and W.M. Wonham. ”Supervisory control of
a class of discrete-event processes,” In SIAM J. on
Control and Optimization, vol.25 N. 1, pp. 206–230,
1987.
K. Rohloff. ”Sensor failure tolerant supervisory control”
Proc. of the 44th IEEE Conf. on Decision and Control
and the European Control Conf. 2005, Seville, Spain,
pp. 3493–3498, December 2005.
I. Romanovski and P.E. Caines. ”On the supervisory con-
trol of multi-agent product systems” Proc. of the
41st IEEE Conf. on Decision and Control, Las Vegas,
Nevada USA, pp. 1181–1186, December 2002.
I. Romanovski and P.E. Caines. ”Multi-Agent product sys-
tems: Controllability and Non-blocking properties”
Accepted at WODES 2006, Ann Arbor, MI, USA, July
2006.
F. Wenck and J.H. Richter. ”A composition oriented per-
spective on controllability of large DES,” Proc. of
WODES 2004, Reims, France, pp. 271–276, 2004.
W.M. Wonham. Notes on Discrete Event Systems, Dept. of
ECE, University of Toronto, Toronto, Canada, 2004.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
488
