PRIUS CONTROL WITH A HYBRID METHOD

Danil Prokhorov

Toyota Technical Center

Toyota Motor Engineering and Manufacturing North America (TEMA)

2350 Green Rd., TRD, Ann Arbor, MI 48105, U.S.A.

Keywords:

HEV powertrain, neurocontroller, extended Kalman ﬁlter.

Abstract:

We describe an application of a computational intelligence method for superior control of the Toyota Prius

hybrid electric vehicle. We are interested in improvement of fuel efﬁciency while reducing emissions. We

describe our approach which is based on recurrent neural networks. The proposed approach is quite general

and applicable to other complex real-world systems.

1 INTRODUCTION

Hybrid powertrains have been gaining popularity due

to their potential to improve signiﬁcantly fuel econ-

omy and reduce undesirable emissions. Control

strategies of the hybrid electric vehicle (HEV) are

more complex than those of the internal combustion

engine-only vehicle because they have to deal with

multiple power sources in sophisticated conﬁgura-

tions. The main function of any control strategy is

power management. It typically implements a high-

level control algorithm which determines the appro-

priate power split between the electric motor and the

engine to minimize fuel consumption and emissions,

while staying within speciﬁed constraints on drivabil-

ity, reliability, battery charge sustenance, etc.

Computational intelligence techniques have pre-

viously been applied to HEV power management by

various authors. A rule-based control was employed

in (Baumann et al., 2000). Fuel economy improve-

ment with a fuzzy controller was demonstrated in

(Schouten et al., 2002), relative to other strategies

which maximized only the engine efﬁciency. An in-

telligent controller combining neural networks and

fuzzy logic which could adapt to different drivers and

drive cycles (proﬁles of the required vehicle speed

over time) was studied in (Baumann et al., 1998).

Recently a neurocontroller was employed in a hybrid

electric propulsion system of a small unmanned aerial

vehicle which resulted in signiﬁcant energy savings

(Harmon et al., 2005).

The references cited above indicate a signiﬁcant

potential for improving HEV performance through

more efﬁcient power management based on applica-

tion of computational intelligence (CI) techniques. To

the best of our knowledge, there has been no work on

improving HEV control by CI methods for the Toy-

ota Prius. Though the Prius efﬁciency is quite high

already, there is a signiﬁcant potential for further im-

provement, as will hopefully become apparent from

this paper.

Unlike traditional hybrid powertrain schemes, se-

ries or parallel, the Prius hybrid implements what is

called the power split scheme. This scheme is quite

innovative and has not been studied extensively yet.

The Prius powertrain uses a planetary gear mecha-

nism to connect an internal combustion engine, an

electric motor and a generator. A highly efﬁcient en-

gine can simultaneously charge the battery through

the generator and propel the vehicle (Figure 1). It is

important to be able to set the engine operating point

to the highest efﬁciency possible and at sufﬁciently

low emission levels of undesirable exhaust gases such

as hydrocarbons, nitrogen oxides and carbon monox-

ide. The motor is physically attached to the ring gear.

It can move the vehicle through the ﬁxed gear ratio

and either assist the engine or propel the vehicle on its

own for low speeds. The motor can also return some

energy to the battery by working as another generator

in the regenerative braking mode.

372

Prokhorov D. (2007).

PRIUS CONTROL WITH A HYBRID METHOD.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 372-375

DOI: 10.5220/0001637703720375

 SciTePress

Figure 1: The Prius car and the main components of the

Toyota hybrid system.

As in our previous work (Prokhorov et al., 2001),

we employ recurrent neural networks (RNN) as con-

trollers and train them for robustness to parametric

and signal uncertainties (known bounded variations of

physical parameters, reference trajectories, measure-

ment noise, etc.). We intend to deploy the trained neu-

rocontroller with ﬁxed weights.

This paper is structured as follows. In the next

section we describe the main elements of our off-line

training. The approach permits us to create an RNN

controller which is ready for deployment with ﬁxed

weights. We then describe our experiments in Sec-

tion 3, followed by our conclusions and directions for

future work.

2 OFF-LINE TRAINING

We adopt the approach of indirect or model based

control development for off-line training. The Prius

simulator is a highly complex, distributed software

which makes training a neurocontroller directly in

the simulator difﬁcult. We implemented a hybrid ap-

proach in which the most essential elements of the

simulator are approximated sufﬁciently accurately by

a neural network model. The NN model is used to

train a neurocontroller by effectively replacing the

simulator. The trained neurocontroller performance

is then veriﬁed in the simulator.

The use of differentiable NN for both model and

controller makes possible application of the industri-

ally proven training method which employs the back-

propagation through time (BPTT) and the extended

Kalman ﬁlter (EKF) for training NN. We refer the

reader to other references for its more comprehensive

account (Prokhorov et al., 2001), (Puskorius et al.,

1996).

3 EXPERIMENTS

We ﬁrst train a NN model to enable off-line train-

ing the neurocontroller as discussed in Section 2. To

do supervised training of the NN model in Figure

2, we gather the input-output pairs from 20 diverse

drive cycles generated in the Prius simulator. We

trained a 25-node structured RNN for 3000 epochs

using the multi-stream EKF (Prokhorov et al., 2001)

and attained the training RMSE of 5·10

−4

(the largest

generalization RMSE was within 20% of the training

RMSE).

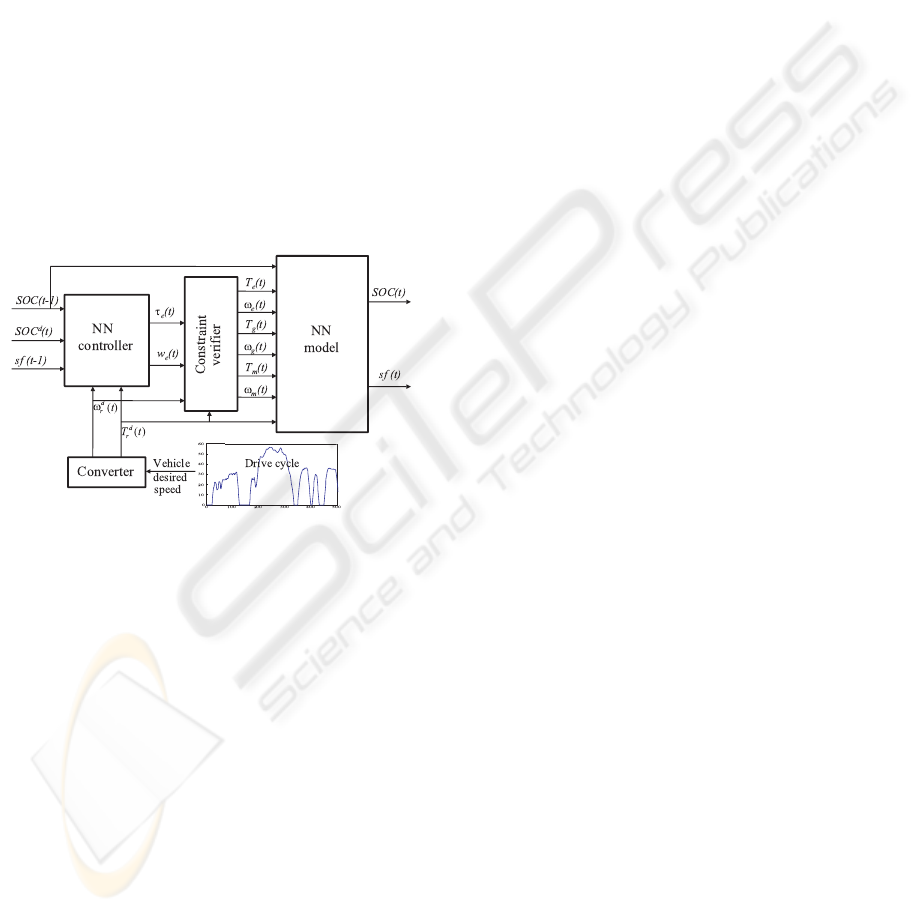
The closed-loop control system for training the

NN controller is shown in Figure 2. The converter

determines the required values of the speed ω

and

the torque T

at the ring gear of the planetary mecha-

nism to achieve the desired vehicle speed speciﬁed in

the drive cycle. This is done on the basis of the Prius

model of motion. The constraint veriﬁer assures sat-

isfaction of various constraints which must hold for

the engine, the motor and the generator speeds and

torques in the planetary gear mechanism, i.e., ω

and

, ω

and T

, ω

and T

, respectively.

Our ﬁrst control goal is to minimize the average

fuel consumed by the engine. However, fuel mini-

mization only is not feasible. The Prius nickel-metal

hydride battery is the most delicate nonlinear compo-

nent of the system with long-term dynamics due to

discharging, charging and temperature variations. It

is important to avoid rapid and deep discharges of the

battery which can drastically reduce its life, requir-

ing costly repairs or even battery replacement. Thus,

the second goal of the HEV control is to maintain the

battery State Of Charge (SOC) throughout the drive

cycle in the safe zone. The SOC can vary between

0.0 (fully discharged) and 1.0 (fully charged), but the

safe zone is typically above 0.4.

We combine the two control goals to ob-

tain cost(t) = λ

(t) + λ

(t)(SOC

(t) − SOC(t))

where sf(t) stands for speciﬁc fuel or fuel rate con-

sumed by the engine at time t, λ

= 1, and λ

(t) ∈

[10, 50] due to about one order of magnitude differ-

ence between values of s f and those of SOC. The

desired SOC

(t) is constant in our experiments for

simplicity. We encourage our controller to pay ap-

proximately the same level of attention to both sf and

SOC, although the optimal balance between λ

and

is yet to be determined. We also penalize reduc-

tions of the SOC below SOC

ﬁve times heavier than

its increases to discourage the controller from staying

PRIUS CONTROL WITH A HYBRID METHOD

373

in the low-SOC region for long. Thus, λ

(t) = 10 if

SOC(t) ≥ SOC

, and λ

(t) = 50 if SOC(t) < SOC

Ultimately, we would also like to minimize emis-

sions of the harmful gases. In this study we attempt to

reduce emissions indirectly through reducing the fuel

consumption because they are often correlated.

Our RNN controller has 5-5R-2 architecture, i.e.,

ﬁve inputs, ﬁve recurrent nodes in the fully recur-

rent hidden layer, and two bipolar sigmoids as output

nodes. The RNN receives as inputs the required out-

put drive speed ω

and torque T

, the current engine

fuel rate s f, the current SOC and the desired SOC

SOC

(see Figure 2; the desired fuel rate is implicit,

and it is set to zero). The RNN produces two con-

trol signals in the range of ±1. The ﬁrst output is the

engine torque τ

, and the second output is the engine

speed w

which become T

and ω

, respectively, after

passing through the constraint veriﬁer.

Figure 2: Block diagram of the closed-loop system for train-

ing the NN controller. The converter determines the re-

quired values of speed ω

and torque T

at the ring gear

of the planetary mechanism to achieve the desired vehicle

speed proﬁle. The constraint veriﬁer makes sure not only

that the torques and speeds are within their speciﬁed physi-

cal limits but also that they are consistent with constraints of

the planetary gear mechanism. The trained NN model takes

care of the remaining complicated dynamics of the plant.

The feedback loop is closed via SOC and the fuel rate sf,

but the required ω

and T

are guaranteed to be achieved

through the appropriate design of the constraint veriﬁer.

Our RNN controller is trained off-line using the

multi-stream EKF algorithm described in Section 2.

When training of our NN controller from Figure 2 is

ﬁnished, we can deploy it inside the high-ﬁdelity sim-

ulator which approximates well behavior of the real

Prius and all its powertrain components. As expected,

we observed some differences between the neurocon-

troller performance in the closed loop with the NN

model and its performance in the high-ﬁdelity simu-

lator because the NN model and the veriﬁer only ap-

proximate the simulator’s behavior. Our results below

pertain to the simulator, rather than its NN approxi-

mation.

The basic idea of the current Prius HEV control

logic is discussed in (Hermance, 1999). When the

power demand is low and the battery SOC is sufﬁ-

ciently high, the motor powers the vehicle. As the

power demand and vehicle speed increase, or the SOC

reduces below a threshold, the engine is started (the

generator may help the motor start the engine). The

engine power is split between propelling the vehi-

cle and charging the battery through the generator.

As the power demand continues to grow, the engine

might not be able to stay within its efﬁciency limits.

In those cases the motor can provide power assist by

driving the wheels to keep the engine efﬁciency rea-

sonably high, as long as the battery can supply the re-

quired power. During decelerations the motor is com-

manded to operate as a generator to recharge the bat-

tery, thereby implementing regenerative braking.

It is hard to make this rule-based strategy opti-

mal for such a complex powertrain. Signiﬁcant aver-

aging over drive cycles with quite different behavior

compromising the best achievable performance is un-

avoidable. We believe that a strategy based on a data-

driven learning system should be able to beat the rule-

based strategy because of its ability to discern differ-

ences in driving patterns and take advantage of them

for improved performance.

We compare our RNN controller trained for ro-

bustness with the rule-based control strategy of the

Prius on 20 drive cycles including both standard

cycles (required by government agencies) and non-

standard cycles (e.g., random driving patterns). Our

RNN controller is better by 15% on average than the

rule-based controller in terms of fuel efﬁciency, and it

appears to be slightly better than the rule-based con-

troller in terms of its emissions on long drive cycles.

It also reduces variance of the SOC over the drive cy-

cle by at least 20%.

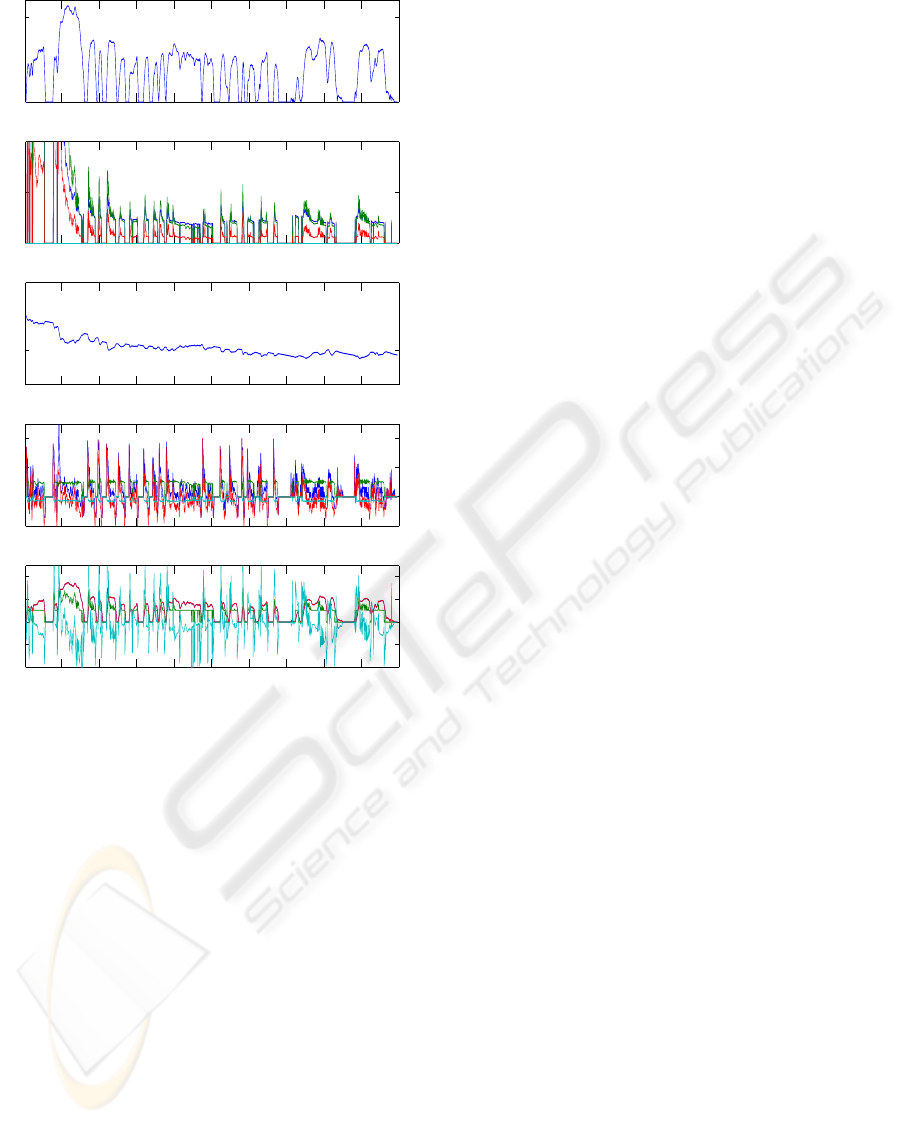
Figure 3 shows an example of our results. It is

a fragment of a long drive cycle (the total length is

12, 700 seconds). Our advantage appears to be in the

more efﬁcient usage of the engine. The engine efﬁ-

ciency is 32% vs. 29% for the rule-based controller.

We also achieved a big improvement in the genera-

tor efﬁciency: 77% vs. 32%, with other component

efﬁciencies remaining basically unchanged.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

374

200 400 600 800 1000 1200 1400 1600 1800 2000

vehicle speed

200 400 600 800 1000 1200 1400 1600 1800 2000

0.005

0.01

emissions

200 400 600 800 1000 1200 1400 1600 1800 2000

0.6

0.8

soc

200 400 600 800 1000 1200 1400 1600 1800 2000

−100

100

200

torques

200 400 600 800 1000 1200 1400 1600 1800 2000

−400

−200

200

400

speeds

Figure 3: A 2000-second fragment of a long city drive cycle

illustrating the typical performance of our RNN controller.

The initial segment (from 0 to ∼ 300 seconds) has signiﬁ-

cant unavoidable emissions due to the engine cold start. The

speed ω

and the torque T

are the blue lines, ω

and T

are

the green lines, the ω

and T

are the red lines, and ω

and

are the cyan lines. Note that ω

= ω

due to the system

design constraint.

4 CONCLUSION

We illustrate our approach to training neurcontrollers

on the Toyota Prius HEV through a high-ﬁdelity sim-

ulation, which is done for the ﬁrst time by methods of

computational intelligence and with results improved

over those of the existing controller. Our approach is

applicable to many real-world control problems.

REFERENCES

Baumann, B., Rizzoni, G., and Washington, G. N. (1998).

Intelligent control of hybrid vehicles using neural net-

works and fuzzy logic. In SAE Technical Paper

981061, SAE Int. Cong. and Exposition. SAE Press.

Baumann, B. M., Washington, G. N., Glenn, B. C., and Riz-

zoni, G. (2000). Mechatronic design and control of

hybrid electric vehicles. IEEE/ASME Transactions on

Mechatronics, 5(1):58–72.

Harmon, F., Frank, A., and Joshi, S. (2005). The control of a

parallel hybrid-electric propulsion system for a small

unmanned arial vehicle using a cmac neural network.

Neural Networks, 18(5/6):772–780.

Hermance, D. (1999). Toyota hybrid system. In SAE

TOPTEC Conference Proc., Albany, NY. SAE Press.

Prokhorov, D. V., Puskorius, G. V., and Feldkamp, L. A.

(2001). Dynamical neural networks for control. In A

Field Guide to Dynamical Recurrent Networks, Edited

by J. Kolen and S. Kremer. IEEE Press.

Puskorius, G. V., Feldkamp, L. A., and L. I. Davis, J.

(1996). Dynamic neural network methods applied

to on-vehicle idle speed control. Proceedings of the

IEEE, 84(10):1407–1420.

Schouten, N., Salman, M., and Kheir, N. (2002). Fuzzy

logic control for parallel hybrid vehicles. IEEE Trans-

actions on Control Systems Technology, 10(3):460–

468.

PRIUS CONTROL WITH A HYBRID METHOD

375