
MINIMIZATION OF l
2
-SENSITIVITY FOR 2-D
SEPARABLE-DENOMINATOR STATE-SPACE DIGITAL FILTERS
SUBJECT TO l
2
-SCALING CONSTRAINTS USING A LAGRANGE
FUNCTION AND A BISECTION METHOD
Takao Hinamoto, Yukihiro Shibata and Masayoshi Nakamoto
Graduate School of Engineering, Hiroshima University, Higashi-Hiroshima 739-8527, Japan
Keywords:
Two-dimensional (2-D) state-space digital filters, separable denominator, l
2
-sensitivity, l
2
-scaling constraints,
scaling-constrained sensitivity minimization, optimal realization.
Abstract:
The problem of minimizing l
2
-sensitivity subject to l
2
-scaling constraints for two-dimensional (2-D)
separable-denominator state-space digital filters is investigated. The coefficient sensitivity of the filter is anal-
ized by using a pure l
2
-norm. An iterative algorithm for minimizing an l
2
-sensitivity measure subject to
l
2
-scaling constraints is then explored by introducing a Lagrange function and utilizing an efficient bisection
method. A numerical example is also presented to illustrate the utility of the proposed technique.
1 INTRODUCTION
In the fixed-point finite-word-length (FWL) imple-
mentation of recursive digital filters, the character-
istics of an actual transfer function deviate from the
original ones due to either truncation or rounding of
filter coefficients. So far, several techniques for syn-
thesizing two-dimensional (2-D) filter structures with
low coefficient sensitivity have been reported (Kawa-
mata et al., 1987)-(Hinamoto and Sugie, 2002). Some
of them use a sensitivity measure evaluated by a mix-
ture of l
1
/l
2
-norms (Kawamata et al., 1987; Hinamoto
et al., 1992; Hinamoto and Takao, 1992), while the
others rely on the use of a pure l
2
-norm (Li, 1998;
Hinamoto et al., 2002; Hinamoto and Sugie, 2002).
Moreover, minimization of frequency-weighted sen-
sitivity for 2-D state-space digital filters has been
considered in accordance with both a mixed l
1
/l
2
-
sensitivity measure and a pure l
2
-sensitivity measure
(Hinamoto et al., 1999). The l
2
-sensitivity minimiza-
tion is more natural and reasonable than the conven-
tional l
1
/l
2
-mixed sensitivity minimization, but it is
technically more challenging. Alternatively, a state-
space digital filter with l
2
-scaling constraints is ben-
eficial for suppressing overflow oscillations (Mullis
and Roberts, 1976; Hwang, 1977). However, satis-
factory solution methods for l
2
-sensitivity minimiza-
tion subject to l
2
-scaling constraints are still needed
(Hinamoto et al., 2004; Hinamoto et al., 2005).
In this paper, an l
2
-sensitivity minimization
problem subject to l
2
-scaling constraints for 2-D
separable-denominator digital filters is formulated.
An efficient iterative algorithm is explored to solve
the constrained optimization problem directly. This
is performed by applying a Lagrange function and an
efficient bisection method. Computer simulation re-
sults by a numerical example demonstrate the validity
and effectiveness of the proposed technique.
2 SENSITIVITY ANALYSIS
There is no loss of generality in assuming that a
2-D digital filter which is separable in the denom-
inator can be described by the Roesser local state-
space (LSS) model {A
1
,A
2
,A
4
,b
1
,b
2
,c
1
,c
2
,d}
m+n
(Roesser, 1975; Hinamoto, 1980) as
x
h
(i+ 1, j)
x
v
(i, j+ 1)
=
A
1
A
2
0 A
4
x
h
(i, j)
x
v
(i, j)
+
b
1
b
2
u(i,j)
y(i, j) =
c
1
c
2
x
h
(i, j)
x
v
(i, j)
+ du(i, j)
(1)
where x
h
(i, j) is an m × 1 horizontal state vector,
x
v
(i, j) is an n × 1 vertical state vector, u(i, j) is a
scalar input, y(i, j) is a scalar output, and A
1
, A
2
, A
4
,
190
Hinamoto T., Shibata Y. and Nakamoto M. (2007).
MINIMIZATION OF l2-SENSITIVITY FOR 2-D SEPARABLE-DENOMINATOR STATE-SPACE DIGITAL FILTERS SUBJECT TO l2-SCALING CON-
STRAINTS USING A LAGRANGE FUNCTION AND A BISECTION METHOD.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 190-195
DOI: 10.5220/0001638301900195
Copyright
c
SciTePress

b
1
, b
2
, c
1
, c
2
, and d are real constant matrices of ap-
propriate dimensions. The LSS model in (1) is as-
sumed to be asymptotically stable, separately locally
controllable and separately locally observable (Kung
et al., 1977). The transfer function of the LSS model
in (1) is given by
H(z
1
,z
2
)
=
c
1
c
2
z
1
I
m
− A
1
−A
2
0 z
2
I
n
− A
4
−1
b
1
b
2
+ d
=
1 c
1
(z
1
I
m
− A
1
)
−1
·
d c
2
b
1
A
2
1
(z
2
I
n
− A
4
)
−1
b
2
.
(2)
Definition 1 : Let X be an m×n real matrix and let
f(X) be a scalar complex function of X, differentiable
with respect to all the entries of X. The sensitivity
function of f with respect to X is then defined as
S
X
=
∂f
∂X
with (S
X
)
ij
=
∂f
∂x
ij
(3)
where x
ij
denotes the (i, j)th entry of the matrix X.
With these notations, it is easy to show that
∂H(z
1
,z
2
)
∂A
1
= Q
T
(z
1
)F
T
(z
1
,z
2
)
∂H(z
1
,z
2
)
∂A
2
= Q
T
(z
1
)P
T
(z
2
)
∂H(z
1
,z
2
)
∂A
4
= G
T
(z
1
,z
2
)P
T
(z
2
)
∂H(z
1
,z
2
)
∂b
1
= Q
T
(z
1
)
∂H(z
1
,z
2
)
∂b
2
= G
T
(z
1
,z
2
)
∂H(z
1
,z
2
)
∂c
T
1
= F (z
1
,z
2
)
∂H(z
1
,z
2
)
∂c
T
2
= P(z
2
)
(4)
where
F (z
1
,z
2
) = (z
1
I
m
− A
1
)
−1
[b
1
+ A
2
P(z
2
)]
G(z
1
,z
2
) = [c
2
+ Q(z
1
)A
2
](z
2
I
n
− A
4
)
−1
P(z
2
) = (z
2
I
n
− A
4
)
−1
b
2
, Q(z
1
) = c
1
(z
1
I
m
− A
1
)
−1
.
The term d and the sensitivity with respect to it are
coordinate independent, therefore they are neglected
here.
Definition 2 : Let X(z
1
,z
2
) be an m × n complex
matrix valued function of the complex variables z
1
and z
2
. The l
p
-norm of X(z
1
,z
2
) is then defined as
||
X
||
p
=
1
(2πj)
2
Γ
2
||
X(z
1
,z
2
)
||
p
F
dz
1
dz
2
z
1
z
2
1/p
(5)
where ||X(z
1
,z
2
)||
F
is the Frobenius norm of the ma-
trix X(z
1
,z
2
) defined by
||
X(z
1
,z
2
)
||
F
=
"
m
∑
p=1
n
∑
q=1
x
pq
(z
1
,z
2
)
2
#
1/2
.
The overall l
2
-sensitivity measure is now defined
by
M
2
=
∂H(z
1
,z
2
)
∂A
1
2
2
+
∂H(z
1
,z
2
)
∂A
4
2
2
+
∂H(z
1
,z
2
)
∂b
1
2
2
+
∂H(z
1
,z
2
)
∂b
2
2
2
+
∂H(z
1
,z
2
)
∂c
T
1
2
2
+
∂H(z
1
,z
2
)
∂c
T
2
2
2
+
∂H(z
1
,z
2
)
∂A
2
2
2
.
(6)
From (4)-(6), it follows that
M
2
= tr
M
A
1
+M
A
4
+W
h
+W
v
+K
h
+K
v
+tr[W
h
]tr[K
v
]
(7)
where
M
A
1
=
1
(2πj)
2
|z
1
|=1 |z
2
|=1
[F(z
−1
1
,z
−1
2
)Q(z
−1
1
)]
·[Q
T
(z
1
)F
T
(z
1
,z
2
)]
dz
1
dz
2
z
1
z
2
M
A
4
=
1
(2πj)
2
|z
1
|=1 |z
2
|=1
[G
T
(z
1
,z
2
)P
T
(z
2
)]
·[P(z
−1
2
)G(z
−1
1
,z
−1
2
)]
dz
1
dz
2
z
1
z
2
K
h
=
1
(2πj)
2
|z
1
|=1 |z
2
|=1
F(z
1
,z
2
)F
∗
(z
1
,z
2
)
dz
1
dz
2
z
1
z
2
K
v
=
1
2πj
|z
2
|=1
P(z
2
)P
∗
(z
2
)
dz
2
z
2
W
h
=
1
2πj
|z
1
|=1
Q
∗
(z
1
)Q(z
1
)
dz
1
z
1
W
v
=
1
(2πj)
2
|z
1
|=1 |z
2
|=1
G
∗
(z
1
,z
2
)G(z
1
,z
2
)
dz
1
dz
2
z
1
z
2
.
The matrices K = K
h
⊕ K
v
and W = W
h
⊕ W
v
are
called the local controllability Gramian and local ob-
sevability Gramian, respectively, and can be obtained
MINIMIZATION OF l2-SENSITIVITY FOR 2-D SEPARABLE-DENOMINATOR STATE-SPACE DIGITAL FILTERS
SUBJECT TO l2-SCALING CONSTRAINTS USING A LAGRANGE FUNCTION AND A BISECTION METHOD
191

by solving the following Lyapunov equations (Kawa-
mata and Higuchi, 1986):
K
v
= A
4
K
v
A
T
4
+ b
2
b
T
2
K
h
= A
1
K
h
A
T
1
+ A
2
K
v
A
T
2
+ b
1
b
T
1
W
h
= A
T
1
W
h
A
1
+ c
T
1
c
1
W
v
= A
T
4
W
v
A
4
+ A
T
2
W
h
A
2
+ c
T
2
c
2
.
(8)
Apply the following eigenvalue-eigenvector decom-
positions:
K
v
=
n
∑
i=1
σ
v
i
u
i
u
T
i
, W
h
=
m
∑
i=1
σ
h
i
v
i
v
T
i
(9)
where σ
v
i
and u
i
(σ
h
i
and v
i
) are the ith eigenvalue and
eigenvector of K
v
(W
h
), respectively. Then, we can
write (7) as (Hinamoto and Sugie, 2002)
M
2
=
n
∑
i=0
σ
v
i
tr[W
h
i
(I
m
)] +
m
∑
i=0
σ
h
i
tr[K
v
i
(I
n
)]
+tr[W
h
+W
v
+K
h
+K
v
] + tr[W
h
]tr[K
v
]
(10)
where σ
v
0
= σ
h
0
= 1,
˜u
i
=
b
1
for i = 0
A
2
u
i
for i ≥ 1
˜v
i
=
c
T
2
for i = 0
A
T
2
v
i
for i ≥ 1
and an m × m matrix W
h
i
(P
1
) and an n × n matrix
K
v
i
(P
4
) are obtained by solving the following Lya-
punov equations:
W
h
i
(P
1
) ∗
∗ ∗
=
A
1
˜u
i
c
1
0 A
1
W
h
i
(P
1
) ∗
∗ ∗
·
A
1
˜u
i
c
1
0 A
1
T
+
0 0
0 P
1
K
v
i
(P
4
) ∗
∗ ∗
=
A
4
0
b
2
˜v
T
i
A
4
T
K
v
i
(P
4
) ∗
∗ ∗
·
A
4
0
b
2
˜v
T
i
A
4
+
"
0 0
0 P
−1
4
#
.
3 SENSITIVITY MINIMIZATION
3.1 Problem Formulation
The following class of state-space coordinate trans-
formations can be used without affecting the input-
output map:
x
h
(i, j)
x
v
(i, j)
=
T
1
0
0 T
4
−1
x
h
(i, j)
x
v
(i, j)
(11)
where T
1
and T
4
are m × m and n × n nonsingular
constant matrices, respectively. Performing this coor-
dinate transformation to the LSS model in (1) yields a
new realization {
A
1
,A
2
,A
4
,b
1
,b
2
,c
1
,c
2
,d}
m+n
char-
acterized by
A
1
= T
−1
1
A
1
T
1
, A
2
= T
−1
1
A
2
T
4
A
4
= T
−1
4
A
4
T
4
, b
1
= T
−1
1
b
1
b
2
= T
−1
4
b
2
, c
1
= c
1
T
1
, c
2
= c
2
T
4
K
h
= T
−1
1
K
h
T
−T
1
, K
v
= T
−1
4
K
v
T
−T
4
W
h
= T
T
1
W
h
T
1
,
W
v
= T
T
4
W
v
T
4
.
(12)
For the new realization, the l
2
-sensitivity measure M
2
in (10) is changed to
M
2
(P) =
n
∑
i=0
σ
v
i
tr[W
h
i
(P
1
)P
−1
1
] +
m
∑
i=0
σ
h
i
tr[K
v
i
(P
4
)P
4
]
+tr[W
h
P
1
+W
v
P
4
+K
h
P
−1
1
+K
v
P
−1
4
]
+tr[W
h
P
1
]tr[K
v
P
−1
4
]
(13)
where P = P
1
⊕ P
4
and P
i
= T
i
T
T
i
for i = 1,4.
If l
2
-norm dynamic-range scaling constraints
are imposed on the new local state vector
[
x
h
(i, j)
T
, x
v
(i, j)
T
]
T
, then
(K
h
)
ii
= (T
−1
1
K
h
T
−T
1
)
ii
= 1
(
K
v
)
j j
= (T
−1
4
K
v
T
−T
4
)
j j
= 1
(14)
are required for i = 1,2,··· ,m and j = 1,2,··· ,n.
From the above arguments, the problem is now
formulated as follows: For given A
1
, A
2
, A
4
, b
1
, b
2
,
c
1
and c
2
, obtain an (m + n) × (m + n) nonsingular
matrix T = T
1
⊕ T
4
which minimizes (13) subject to
l
2
-scaling constraints in (14).
3.2 Problem Solution
If we sum up m constraints and n constraints in (14)
separately, then we have
tr[K
h
P
−1
1
] = m, tr[K
v
P
−1
4
] = n. (15)
Consequently, the problem of minimizing M
2
(P) in
(13) subject to the constraints in (14) can be relaxed
into the problem
minimize M
2
(P) in (13)
subject to tr[K
h
P
−1
1
] = m and tr[K
v
P
−1
4
] = n.
(16)
In order to solve (16), we define a Lagrange function
of the problem as
J(P, λ
1
,λ
4
) = M
2
(P) + λ
1
(tr[K
h
P
−1
1
] − m)
+λ
4
(tr[K
v
P
−1
4
] − n)
(17)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
192
where λ
1
and λ
4
are Lagrange multipliers. It is
well known that the solution of problem (16) must
satisfy the Karush-Kuhn-Tucker (KKT) conditions
∂J(P, λ
1
,λ
4
)/∂P
i
= 0 for i = 1,4 where the gradients
are found to be
∂J(P, λ
1
,λ
4
)
∂P
1
= F
1
(P) − P
−1
1
F
2
(P
1
,λ
1
)P
−1
1
∂J(P, λ
1
,λ
4
)
∂P
4
= F
3
(P
4
) − P
−1
4
F
4
(P,λ
4
)P
−1
4
(18)
with
F
1
(P) =
n
∑
i=0
σ
v
i
K
h
i
(P
1
) + (1+ tr[K
v
P
−1
4
])W
h
F
2
(P
1
,λ
1
) =
n
∑
i=0
σ
v
i
W
h
i
(P
1
) + (λ
1
+ 1)K
h
F
3
(P
4
) =
m
∑
i=0
σ
h
i
K
v
i
(P
4
) +W
v
F
4
(P,λ
4
) =
m
∑
i=0
σ
h
i
W
v
i
(P
4
) + (λ
4
+ 1+ tr[W
h
P
1
])K
v
K
h
i
(P
1
) ∗
∗ ∗
=
A
1
0
˜u
i
c
1
A
1
T
K
h
i
(P
1
) ∗
∗ ∗
·
A
1
0
˜u
i
c
1
A
1
+
"
0 0
0 P
−1
1
#
W
v
i
(P
4
) ∗
∗ ∗
=
A
4
b
2
˜v
T
i
0 A
4
W
v
i
(P
4
) ∗
∗ ∗
·
A
4
b
2
˜v
T
i
0 A
4
T
+
0 0
0 P
4
.
Hence the above KKT conditions become
P
1
F
1
(P)P
1
= F
2
(P
1
,λ
1
)
P
4
F
3
(P
4
)P
4
= F
4
(P,λ
4
).
(19)
Two equations in (19) are highly nonlinear with re-
spect to P
1
and P
4
. An effective approach to solving
two equations in (19) is to relax them into the follow-
ing recursive second-order matrix equations:
P
(i+1)
1
F
1
(P
(i)
)P
(i+1)
1
= F
2
(P
(i)
1
,λ
(i+1)
1
)
P
(i+1)
4
F
3
(P
(i)
4
)P
(i+1)
4
= F
4
(P
(i)
,λ
(i+1)
4
)
(20)
with the initial condition P
(0)
= P
(0)
1
⊕ P
(0)
4
= I
m+n
.
The solutions P
(i+1)
1
and P
(i+1)
4
of (20) are given by
P
(i+1)
1
= F
−
1
2
1
(P
(i)
)[F
1
2
1
(P
(i)
)F
2
(P
(i)
1
,λ
(i+1)
1
)
·F
1
2
1
(P
(i)
)]
1
2
F
−
1
2
1
(P
(i)
)
P
(i+1)
4
= F
−
1
2
3
(P
(i)
4
)[F
1
2
3
(P
(i)
4
)F
4
(P
(i)
,λ
(i+1)
4
)
·F
1
2
3
(P
(i)
4
)]
1
2
F
−
1
2
3
(P
(i)
4
)
(21)
respectively. Here, Lagrange multipliers λ
(i+1)
1
and
λ
(i+1)
4
can be efficiently obtained using a bisection
method so that
f
1
(λ
(i+1)
1
) = m− tr[
˜
K
(i)
h
˜
F
(i)
2
(λ
(i+1)
1
)] = 0
f
4
(λ
(i+1)
4
) = n − tr[
˜
K
(i)
v
˜
F
(i)
4
(λ
(i+1)
4
)] = 0
(22)
are satisfied where
˜
K
(i)
h
= F
1
2
1
(P
(i)
)K
h
F
1
2
1
(P
(i)
)
˜
K
(i)
v
= F
1
2
3
(P
(i)
4
)K
v
F
1
2
3
(P
(i)
4
)
˜
F
(i)
2
(λ
(i+1)
1
) = [F
1
2
1
(P
(i)
)F
2
(P
(i)
1
,λ
(i+1)
1
)F
1
2
1
(P
(i)
)]
−
1
2
˜
F
(i)
4
(λ
(i+1)
4
) = [F
1
2
3
(P
(i)
4
)F
4
(P
(i)
,λ
(i+1)
4
)F
1
2
3
(P
(i)
4
)]
−
1
2
.
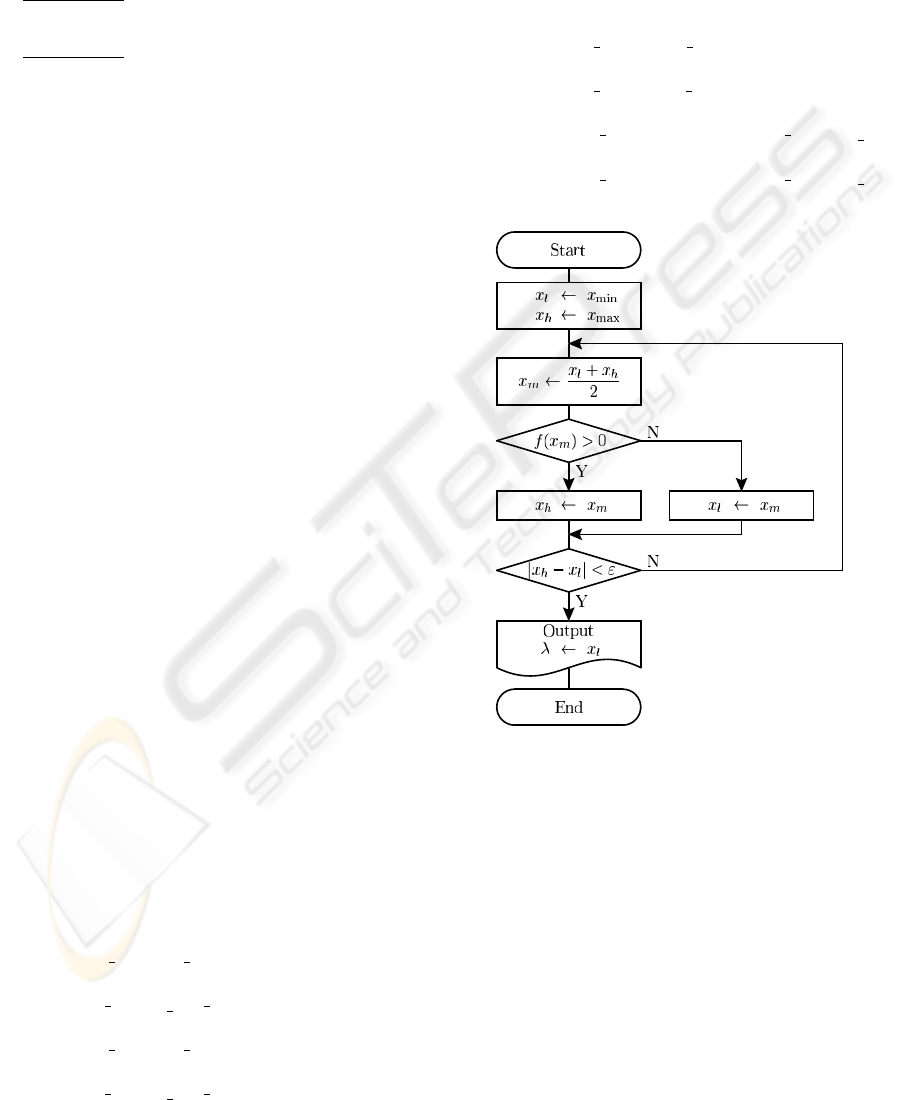
Figure 1: A flow chart of the bisection method.
A flow chart of the above bisection method is
shown in Fig. 1. The iteration process continues until
|J(P
(i+1)
,λ
(i+1)
1
,λ
(i+1)
4
) − J(P
(i)
,λ
(i)
1
,λ
(i)
4
)| < ε (23)
is satisfied for a prescribed tolerance ε > 0. If the
iteration is terminated at step i, then P
(i)
is viewed as
a solution point.
Once positive-definite symmetric matrices P
1
and
P
4
satisfying tr[K
1
P
−1
1
] = m and tr[K
4
P
−1
4
] = n were
obtained, it is possible to construct an m× m orthog-
onal matrix U
1
and an n× n orthogonal matrix U
4
so
that matrix T = P
1/2
1
U
1
⊕ P
1/2
4
U
4
satisfies L
2
-scaling
constraints in (14). (Hinamoto et al., 2005)
MINIMIZATION OF l2-SENSITIVITY FOR 2-D SEPARABLE-DENOMINATOR STATE-SPACE DIGITAL FILTERS
SUBJECT TO l2-SCALING CONSTRAINTS USING A LAGRANGE FUNCTION AND A BISECTION METHOD
193

4 ILLUSTRATIVE EXAMPLE
Suppose that a 2-D separable-denominator digital fil-
ter {A
o
1
,A
o
2
,A
o
4
,b
o
1
,b
o
2
,c
o
1
,c
o
2
,d}
3+3
in (1) is specified
by
A
o
1
=
0 1 0
0 0 1
0.599655 −1.836929 2.173645
A
o
2
=
0.064564 0.033034 0.012881
0.091213 0.110512 0.102759
0.097256 0.151864 0.172460
A
o
4
=
0 0 0.564961
1 0 −1.887939
0 1 2.280029
b
o
1
=
0.047053
0.062274
0.060436
, b
o
2
=
1
0
0
c
o
1
=
1 0 0
c
o
2
=
0.016556 0.012550 0.008243
d = 0.019421.
By performing the l
2
-scaling for the above LSS
model with a diagonal coordinate-transformation ma-
trix T
o
= T
o
1
⊕ T
o
4
where
T
o
1
= diag{0.992289,0.987696,0.964582}
T
o
4
= diag{4.636056,10.980193,8.012802}
we obtained
A
1
=
0.000000 0.995371 0.000000
0.000000 0.000000 0.976599
0.616880 −1.880945 2.173645
A
2
=
0.301648 0.365538 0.104015
0.428136 1.228560 0.833645
0.467440 1.728723 1.432628
A
4
=
0.000000 0.000000 0.976460
0.422220 0.000000 −1.377725
0.000000 1.370331 2.280029
b
1
=
0.047419 0.063050 0.062655
T
b
2
=
0.215701 0.000000 0.000000
T
c
1
=
0.992289 0.000000 0.000000
c
2
=
0.076755 0.137801 0.066050
and the l
2
-sensitivity of the scaled LSS model was
found to be
M
2
= 4526.0790.
Choosing P
(0)
= P
(0)
1
⊕ P
(0)
4
= I
6
in (21) as initial
estimate, x
min
= −2
20
and x
max
= 2
20
in the bisection
method, and tolerance ε = 10
−8
in Fig. 1 and (23), it
took the proposed algorithm 15 iterations to converge
to the solution P
opt
= P
opt
1
⊕ P
opt
4
where
P
opt
1
=
0.992455 0.702756 0.373871
0.702756 0.724033 0.597920
0.373871 0.597920 0.674661
P
opt
4
=
2.200512 −2.005367 1.676709
−2.005367 1.913721 −1.647192
1.676709 −1.647192 1.480797
or equivalently, T
opt
= T
opt
1
⊕ T
opt
4
where
T
opt
1
=
−0.975337 −0.066061 0.191859
−0.619458 0.147201 0.564479
−0.291519 0.450550 0.621839
T
opt
4
=
−0.799684 0.585116 −1.103928
0.493843 −0.684596 1.095978
−0.336031 0.804236 −0.849167
.
The minimized l
2
-sensitivity measure in (17) corre-
sponding to the above solution was found to be
J(P
opt
,λ
1
,λ
4
) = 101.0064
with λ
1
= 4.786834 and λ
4
= −4.094596. By substi-
tuting T = T
opt
obtained above into (12), the optimal
state-space filter structure that minimizes (13) subject
to the l
2
-scaling constraints in (14) was synthesized as
A
1
=
0.694418 −0.112298 −0.412379
−0.096981 0.765920 −0.345179
0.282990 0.456524 0.713306
A
2
=
0.138105 −0.073790 0.140661
−0.132057 0.634682 −0.262494
0.158022 −0.104957 0.516782
A
4
=
0.699418 −0.018435 0.273811
−0.091049 0.837579 0.358967
−0.257686 −0.254075 0.743031
b
1
=
−0.038277 0.028296 0.062312
T
b
2
=
−0.758218 0.129041 0.422255
T
c
1
=
−0.967816 −0.065551 0.190380
c
2
=
−0.015522 0.003691 0.010209
whose horizontal and vertical controllability Grami-
ans were given by
K
h
opt
=
1.000000 −0.090933 −0.400242
−0.090933 1.000000 0.400242
−0.400242 0.400242 1.000000
K
v
opt
=
1.000000 −0.126238 −0.520618
−0.126238 1.000000 0.520618
−0.520618 0.520618 1.000000
.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
194

Profile of the l
2
-sensitivity measure, and profile of
the parameters λ
1
and λ
4
during the first 15 iterations
of the proposed algorithm are shown in Figs. 2 and 3,
respectively.
Iterations
J (P ,λ
1
,λ
4
)
Figure 2: l
2
-Sensitivity Performance.
̂
̂
̂
̂
̂
̂
̂
Iterations
λ
1
λ
4
λ
1
λ
4
,
Figure 3: λ
1
and λ
4
Performances.
5 CONCLUSION
The problem of minimizing the l
2
-sensitivity measure
subject to l
2
-scaling constraints for 2-D separable-
denominator state-space digital filters has been for-
mulated. An iterative method for minimizing l
2
-
sensitivity subject to l
2
-scaling constraints has been
explored. This has been performed by using a La-
grange function and an efficient bisection method.
Computer simulation results have demonstrated the
validity and effectiveness of the proposed technique.
REFERENCES
Hinamoto, T. (1980). Realization of a state-space model
from two-dimensional input-output map. IEEE Trans.
Circuits Syst.
Hinamoto, T., Iwata, K., and Lu, W.-S. (2005). State-space
digital filters with minimum l
2
-sensitivity subject to
l
2
-scaling constraints. In Proc. 2005 IEEE Int. Conf.
Acoust., Speech, Signal Processing.
Hinamoto, T., Ohnishi, H., and Lu, W.-S. (2004). Min-
imization of l
2
-sensitivity for 2-d state-space digital
filters subject to l
2
-scaling constraints. In Proc. 2004
IEEE Int. Symp. Circuits Syst.
Hinamoto, T. and Sugie, Y. (2002). l
2
-sensitivity analysis
and minimization of 2-d separable-denominator state-
space digital filters. IEEE Trans. Signal Processing.
Hinamoto, T. and Takao, T. (1992). Synthesis of 2-d state-
space filter structures with low frequency-weighted
sensitivity. IEEE Trans. Circuits Syst. II.
Hinamoto, T., Takao, T., and Muneyasu, M. (1992). Syn-
thesis of 2-d separable-denominator digital filters with
low sensitivity. J. Franklin Institute.
Hinamoto, T., Yokoyama, S., Inoue, T., Zeng, W., and
Lu, W.-S. (2002). Analysis and minimization of
l
2
-sensitivity for linear systems and two-dimensional
state-space filters using general controllability and ob-
servability gramians. IEEE Trans. Circuits Syst. I.
Hinamoto, T., Zempo, Y., Nishino, Y., and Lu, W.-S.
(1999). An analytical approach for the synthesis
of two-dimensional state-space filter structures with
minimum weighted sensitivity. IEEE Trans. Circuits
Syst. I.
Hwang, S. Y. (1977). Minimum uncorrelated unit noise
in state-space digital filtering. IEEE Trans. Acoust.,
Speech, Signal Processing.
Kawamata, M. and Higuchi, T. (1986). Synthesis of 2-d
separable denominator digital filters with minimum
roundoff noise and no overflow oscillations. IEEE
Trans. Circuits Syst.
Kawamata, M., Lin, T., and Higuchi, T. (1987). Minimiza-
tion of sensitivity of 2-d state-space digital filters and
its relation to 2-d balanced realizations. In Proc. 1987
IEEE Int. Symp. Circuits Syst.
Kung, S. Y., Levy, B. C., Morf, M., and Kailath, T. (1977).
New results in 2-d systems theory, part ii: 2-d state-
space models -realization and the notions of control-
lability, observability, and minimality. In Proc. IEEE.
Li, G. (1998). Two-dimensional system optimal realizations
with l
2
-sensitivity minimization. IEEE Trans. Signal
Processing.
Mullis, C. T. and Roberts, R. A. (1976). Synthesis of min-
imum roundoff noise fixed-point digital filters. IEEE
Trans. Circuits Syst.
Roesser, R. P. (1975). A discrete state-space model for lin-
ear image processing. IEEE Trans. Automat. Contr.
MINIMIZATION OF l2-SENSITIVITY FOR 2-D SEPARABLE-DENOMINATOR STATE-SPACE DIGITAL FILTERS
SUBJECT TO l2-SCALING CONSTRAINTS USING A LAGRANGE FUNCTION AND A BISECTION METHOD
195
