DESIGN AND IMPLEMENTATION OF A MONITORING SYSTEM

USING GRAFCET

Adib Allahham and Hassane Alla

GIPSA-Lab, Department of Control, Institute National de Polytechnique de Grenoble

961 Rue de la Houille Blanche - Domaine universitaire BP 46, 38402 Saint Martin D’h

eres, France

Keywords:

Monitoring, Fault detection, Manufacturing systems, Stopwatch automata, Reachability analysis, Grafcet.

Abstract:

A monitoring system based on a stopwatch automaton is proposed to detect the system faults as early as

possible. Each location in the automaton corresponds to a system’s situation. Its time space delimits exactly

the range of the normal behavior in the corresponding system’s situation. The monitoring system detects a

fault when the time space corresponding to the actual system’s situation is violated. The stopwatch automaton

provides a formal foundation to model the system’s behavior and to synthesize the exactly time space in each

location. This paper aims to provide the grafcet monitor that allows to link the design of the monitoring system

of a system with its implementation in a programmable logic controller.

1 INTRODUCTION

Monitoring complex manufacturing systems plays an

important role for economic and security reasons. A

wide variety of methods has been considered this

problem. These methods consider a fault have oc-

curred in a system if a faulty event occurs (Ghazel

et al., 2005), reaching a faulty state (S. H. ZAd and

Wonham, 2003) or more generally violating system

speciﬁcations. Most systems monitor the timed sys-

tem speciﬁcations by using Watchdogs. They detect a

fault if the expected observation is produced early or

late with respect to certain time bounds.

The increasingly stringent requirements in monitor-

ing and fault detection problems lead to the necessity

to detect the fault as early as possible without waiting

the expiration of certain bounds. For that, we have

proposed in (A.allahham and alla, 2006) a monitoring

method which extends the method of residuals, well-

known in continuous system. In (A.allahham and alla,

2006), we have introduced the notion of acceptable

behavior of a system detailed in the following sec-

tion. We model this acceptable behavior by a stop-

watch automaton. In that representation, each loca-

tion corresponds to a state of the system and the arcs

are labeled by switching conditions between the dif-

ferent states. In each state, the differential equations

express the progression or suspension of the task rep-

resented by the stopwatch due to a fault. The time

sub-space in each location represented by a set of al-

gebraic inequalities, delimits the range of stopwatches

in the corresponding system’s situation in the accept-

able behavior. The monitoring system detects a fault

when the system exceeds this time sub-space.

The stopwatch automaton provides a formal basis to

model the system’s behavior and to analyze it in order

to characterize the exact time sub-space in each loca-

tion, corresponding to the acceptable behavior.

In this paper, our objective is to provide the grafcet

model that allows to link the design of monitoring

system of a manufacturing system with its implemen-

tation in the logic controller. We show that the grafcet

fulﬁls not only the sequential speciﬁcation of the ap-

plications but also the continuous behavior speciﬁed

in the monitoring stopwatch automaton.

The grafcet corresponding to monitoring automaton

models a location by a step and a stopwatch by a

timer where the following problem is encountered.

The behavior of a stopwatch goes beyond the abil-

ity of a timer representing the simplest way to include

the time in grafcet model. This problem in turn af-

fects the method to represent the time sub-space as-

sociating to the steps of grafcet. However, we will

show that this problem can be overcome by complet-

220

Allahham A. and Alla H. (2007).

DESIGN AND IMPLEMENTATION OF A MONITORING SYSTEM USING GRAFCET.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 220-225

DOI: 10.5220/0001639102200225

 SciTePress

Execution

Normal

fault

Intermediate

state

Acceptable

behavior

Figure 1: Acceptable behavior of a system.

ing the grafcet by actions associated with steps. Also,

the grafcet will monitor permanently the consistency

of the stopwatches within its acceptable range.

Section 2 describes the acceptable behavior of a

system and its model based on stopwatch automaton.

Our approach is given and used to delimit the time

space characterizing this behavior. In Section 3, the

method to translate a monitoring automaton into a

Grafcet model is detailed. We apply this method in

an illustrative example in Section 4.

2 THE ACCEPTABLE BEHAVIOR

The possible kinds of faults that affect the resources

in a manufacturing system are the permanent faults,

which dispossess a resource’s ability to perform its

task and the intermitting faults. These faults can

appear several times during the task execution and

disappear without any external action on the system

while permanent faults disappear due to a repair of

the fault (Huang et al., 1996). Our work considers

only the intermitting faults that interrupt the task of

a resource. We call it malfunctions and the task sub-

jected to these malfunctions as interruptible task. The

system containing these tasks is called as interrupt-

ible system. Because of malfunctions, an interme-

diate state can appear between a normal state and a

faulty one. In this state, the system can come back

to the normal behavior or it leaves toward a faulty

state (Fig.1). We refer to this behavior by acceptable

behavior. These malfunctions occur often in a man-

ufacturing system, so the system’s designer accepts

to some extent this behavior for productivity motives.

The question to answer is: how the designer takes into

account these malfunctions in his system.

Let be a task Task

∈ Task

int

where Task

int

represents

the set of interruptible tasks in a complex system S.

Task

has a known execution duration [α

, β

] which is

given in the technical characteristics of the resources

that execute Task

or measured directly. Because of

the interruptions resulting from malfunctions, the de-

signer accepts a tolerated duration to execute Task

. It

is given by the interval [α

, γ

) where β

< γ

. We call

[α

, β

] and [α

, γ

) respectively the normal and accept-

able durations of Task

Signals of monitoring

sensors

-1 -

Process + Control

Monitoring System

(Stopwatch automaton

)

Signals of the

system’s control

sensors

Alarm

-2 -

+ orders

Time

execution

Time

Task end

execution

Figure 2: 1- Behavior of an interruptible task 2-

Inputs\Output of monitoring system.

2.1 Monitoring of an Interruptible Task

We refer to the apparition and disappearing of a fault

by its effect on the task execution, then we refer it by

interruption and resuming of the task.

Hypothsis 1 The execution speed is supposed to be

constant or to vary sightly around a mean value. 

Considering the properties of the tasks mentioned

above, we distinguish the behavior of an interruptible

task shown in Figure 2.1. Either Task

is executed

without interruption, then t

∈ [α

, β

] or Task

has

been executed but with several interruptions. After

each interruption, the system resumes from the po-

sition at which it has been interrupted. In this case:

∈ [α

, γ

To monitor Task

, we use the timers x

and y

. The

timers x

and y

have a values ”0” when the task be-

gins. x

will be used to check that T ask

has com-

pleted before the expiration of its tolerated deadline.

is used to monitor the effective time of execution.

Then, Task

is correctly executed if y

∈ [α

, β

] and x

∈ [α

, γ

) when the task end occurs.

The arrows ↓ and ↑ in Figure 2.1 represent respec-

tively the signal of logical sensor which detects the in-

terruption and resuming of Task

. These signals rep-

resent an input of our monitoring system (Fig. 2.2).

2.2 Modeling of an Interruptible System

We use the stopwatch automata SWA to model the in-

terruptible system. It is a class of linear hybrid au-

tomaton where the time derivative of a clock in a lo-

cation can be either 0 or 1 (Cassez and Larsen, 2000).

Deﬁnition 1 A stopwatch automaton is a 7-tuple

(L, l

, X, Σ, A, I,

X) where:

• L is a ﬁnite set of locations, l

: the initial location,

• X is a ﬁnite set of stopwatches,

• Σ is a ﬁnite set of labels,

• A is a ﬁnite set of arcs. a = (l, δ, σ, R, l

) ∈ A is

the arc between the locations l and l

, with the guard

δ ∈ C(X ), the label name σ and the set of stopwatches

to reset R. C(X ) is the set of constraints over X.

DESIGN AND IMPLEMENTATION OF A MONITORING SYSTEM USING GRAFCET

221

Normal execution

Interruption

Initial

•

Alarm

Faulty state

≤

x γ

≤

iii

≤

x γ

•

≤

x γ

≤

•

≤

x γ

≤

x γ

Figure 3: Stopwatch automaton of an interruptible task.

• I ∈ C(X)

maps an invariant to each location,

•

X ∈ ({0, 1}

)

maps an activity to each location. 

• SWA of an interruptible task

We model the acceptable behavior of Task

by the

Stopwatch automaton shown in Fig. 3. The loca-

tion l

indicates that the resource is waiting to start

the task, l

that the resource is executing its task and

that the task is interrupted after having started. In

this automaton, the clock y

in l

does not progress

while x

evolves to express that the task is interrupted

but the time remains progressing. The labels s

and

represent respectively the stop and the resumption

of Task

in the physical system, while label σ

corre-

sponds to the end of this task. ε

which is the always

true event, represents the necessary condition to start

the task. Here it starts immediately.

The guard g

of the arc l

−→ l

expresses that the

interruption can occur at any instant during the ac-

ceptable duration while the guard g

associated to

−→ l

expresses that the resumption must occur be-

fore exceeding the acceptable duration. The execution

of task

, during its acceptable duration is represented

by the guard g

of the arc l

−→ l

Figure 3 shows that Task

leaves the acceptable be-

havior to faulty state l

either from the location l

. The guards of arcs towards l

are identical and

given by g

= ¬g

= (x

= γ

∧ y

< α

). It expresses

the fact that the acceptable duration of execution was

expired and Task

is not executed.

2.3 Time Space State Delimiting the

Acceptable Behavior

The acceptable behavior of a system S is represented

by a stopwatch automaton A. It is obtained by the

composition of the different tasks automata accord-

ing to the system speciﬁcations which represent the

relation between these tasks.

Property 1 The trajectories which lead Task

to the

state l

× (0, 0) from l

× (x

, y

) where x

∈ [α

, γ

)

and y

∈ [α

, β

], represent all the possible evolutions

characterizing the execution of Task

. 

The trajectories speciﬁed in Property 1 represent only

a part of the possible ones. Thus, the synthesis prob-

lem of monitoring can be set as follows: given a stop-

watch automaton A representing a system S, restrict

the possible trajectories of this automaton in a way

that all remaining ones satisfy Property 1, for all the

tasks of S. As a result, we obtain an automaton A

∗

where all its trajectories characterize the acceptable

execution of S. The calculation of the time space con-

taining these trajectories E

∗

of A

∗

is the core of our

synthesis algorithm. This is realized using of the For-

ward and backward reachability analysis. (Alur et al.,

1995)

• Forward analysis of monitoring SWA:

We use the forward analysis operators to calculate all

the possible trajectories in the system. In other words:

the reachable time space E in the automaton A men-

tioned above. The forward operators look for all the

reachable states of a stopwatch automaton from its

initial state remaining in the locations of automaton

while the time progresses or by ﬁring its transitions.

The reachable time space by forward analysis in loca-

tions l

and l

of the automaton shown in Figure 3 is

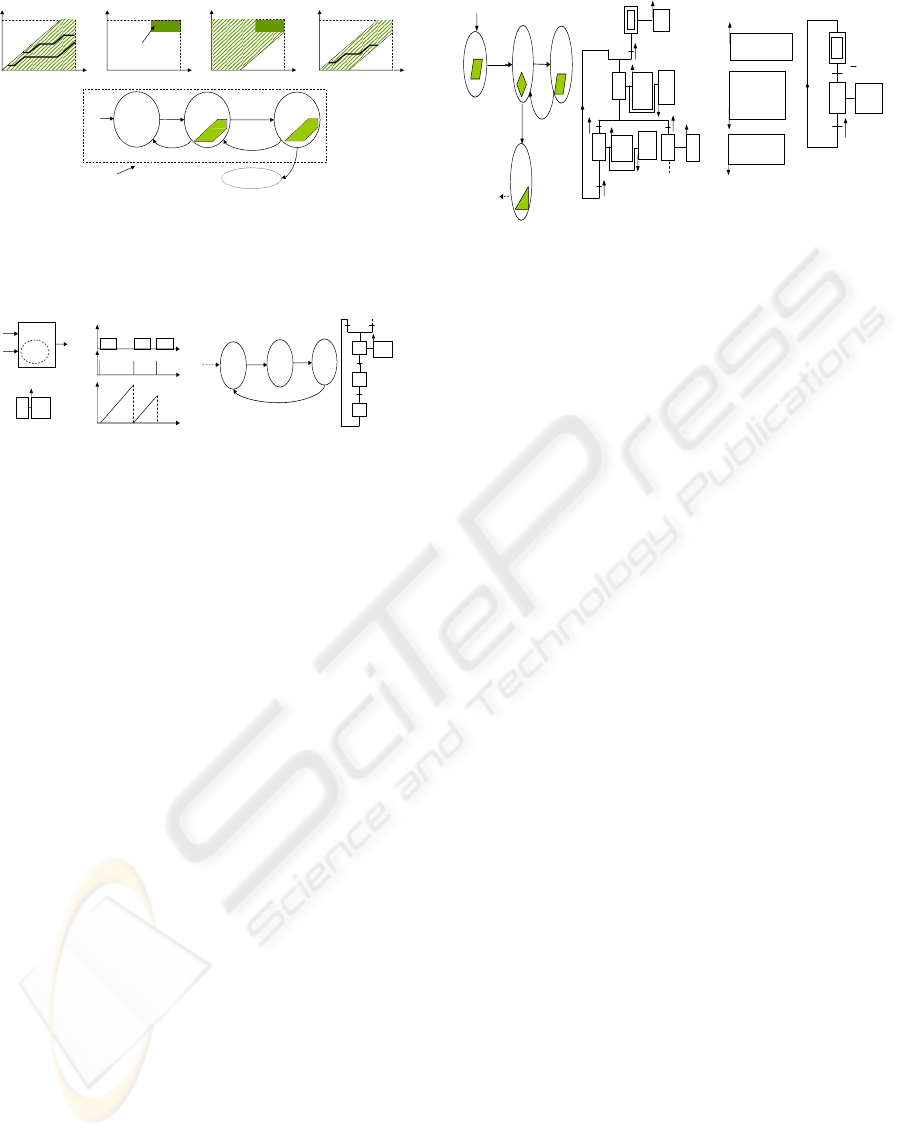
given in Figure 4.1. Note that the values of the stop-

watches given by g

in Figure 3 deﬁne a polyhedron.

We denote it as D

, and call it as the desired space of

Task

(Fig 4.2). Note also that the trajectories spec-

iﬁed in Property 1 lead the task only to D

. These

trajectories represent only a part of the ones which are

contained in reachable time space (Fig. 4.1). Thus,we

must delimit the time space containing only these tra-

jectories to characterize the acceptable execution.

• Backward analysis of monitoring SWA:

It is not hard to see that the time space E

∗

of A

∗

can

be obtained by removing from the time space of A

the states from which system’s evolutions do not lead

to D

of each interruptible task. In other words, one

needs ﬁrst to apply the backward operators (called

as predecessors and annotated as Pre operators) to

the guards of arcs representing the desired space of

all the tasks over the automaton A. Then, E

∗

=E ∩

( Pre(D

)). The intuition behind the using the pre-

decessors operators for a guard representing D

Task

is that we look for all the states that lead to this

space D

from the initial state of A.

Applying the backward analysis for the automaton

given in Figure 3 gives the time space shown in Figure

4.3. The intersection of this space and that of forward

analysis is given in Figure 4.4. It is the space charac-

terizing the execution acceptable of Task

. One of the

trajectories contained in synthesized space (Fig. 4.4)

shows that the task reaches a faulty state, only from

the location l

with the dynamics ˙x = 1 and ˙y = 0. Fig-

ure 4.5 presents the ﬁnal monitoring automaton A

∗

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

222

-2-

-4-

-1-

-3-

−

γα

−

γα

•

Faulty state

•

x:=

y:=

-5-

Figure 4: Time space in l

and l

: (1) reachable by forward

analysis, (2) desired, (3) reachable by backward analysis (4)

delimiting acceptable execution (5) Synthesized Monitoring

automaton of an interruptible task.

C↑

-2 -

•

-3 -

-1 -

•

Figure 5: (1) Timer (2) A part of monitoring automaton (3)

Corresponding grafcet G

3 GRAFCET OF THE

MONITORING SYSTEM

Grafcet and its international standard SFC (CEI/ IEC

60848 revised in 2002) are used for the implementa-

tion of discrete events models for manufacturing sys-

tems and many programmable logic controllers use

it as a programming language. The basic concepts of

the grafcet are: the step, action, transition and its asso-

ciated receptivity (David, 1995). A Boolean variable

is associated with each step. Its value is 1 when

step is active.

The general idea to translate the monitoring automa-

ton A

∗

into a grafcet is to represent each location of

the automaton by a step. The faulty state is also mod-

eled by a step. Let L = {l

, ..., l

} be the set of loca-

tions of A

∗

. The set of steps corresponding to these

locations is denoted by {1, ..., n}. An arc linking two

locations is modeled by a transition linking the two

corresponding steps. The transition receptivity is the

label of the arc. The simplest way to include time in

the grafcet model is to use timer objects, for that, each

stopwatch will be modeled by a timer.

Figure 5 shows a timer (T

) which is typically initial-

ized with a value representing a duration (I

input)

and a control input (C

) for starting the timer. This

timer produces a boolean output (O

). Associating

an impulse action ↑ C

with a step j will activate the

timer T

as soon as ↑ X

= 1. Here, we are not inter-

ested in the logic output of timer, but in the instanta-

neous value of the timer T

denoted by x

, which is

•

x:=

y:=

•

-1 -

x:=

y:=

(3)

(1)

(2)

xxT

iii

δδ

xxT

iii

δδ

-2 -

(1)

(2)

(3)

(1)

-3 -

)

alar

(E .X )∨

)

Figure 6: (1) A part of monitoring automaton (2) G

and

shifting and initiation actions (3) G

model.

supposed to be readable and testable in real time. In

fact, many PLC manufacturers provides products with

timers equipped with functions permitting to read and

test the value x

In these translation rules, the behavior of a stopwatch

goes beyond the ability of a timer. To show that,

we consider the part of monitoring automaton shown

in Figure 5.2. In this automaton the stopwatch x

is newly activate in l

and remains active in l

and

. Translating this model into a grafcet by using the

method described above, gives the model shown in

Figure 5.3 where T

is the timer corresponding to stop-

watch x

. In this grafcet, we activate the timer T

soon as the ↑ X

= 1. T

remains active in steps 2 and

3. However this is not sufﬁcient to represent the be-

havior of the monitoring automaton since an impor-

tant issue is the behavior at the ﬁring the arc of au-

tomaton between l

and l

. The stopwatch x

persists

active after the commutation and has a certain value

at the instant of reaching l

, while there will be an ini-

tialization of the value of corresponding timer T

when

↑ X

= 1 in the grafcet. However, we show that this

problem can be overcome by completing the grafcet

by actions and by using intermediate variables.

• Modeling of stopwatches by timers:

Let us consider that the automaton given in Figure

6.1 follows the behavior given in Figure 7. T

and T

are the timers corresponding to stopwatches x

and y

We express the dynamics ˙x

= 1 and ˙y

= 1 in the lo-

cation l

by associating to step 2 the impulse actions

↑ C

and ↑ C

. These actions will activate T

and T

as soon as ↑ X

= 1. In a similar way, we express the

dynamic ˙x

= 1 in l

. We will now give the method to

represent the behavior of x

and y

whose values are 0

at the entry of l

. Note that the value of x

in a given

location l

or l

is the sum of: the value of x

when the

system reaches this location and the passed time from

the reaching instant to actual one.

The latter item corresponds to the value of timer T

which is activated when the system reaches the step

corresponding to the given location. For the for-

DESIGN AND IMPLEMENTATION OF A MONITORING SYSTEM USING GRAFCET

223

(t )

Figure 7: Representing behavior of stopwatches in grafcet.

mer item, an intermediate variable denoted by δ

and

called as shifting variable is used. δ

is initialized

when the automaton resets to 0 the stopwatch x

. The

value of δ

corresponding to x

) in Figure 7 can be

obtained by associating to the step 2 (Fig. 6.2) the

impulse action ↓ δ

:= δ

+ x

(Shifting action). It

adds to δ

whose initially has the value 0, the value

of x

representing the duration that the grafcet stays

in step 2. The value of δ

corresponding to x

) in

Figure 7 can be obtained by associating to step 3 the

same action. It adds to previous value of δ

the du-

ration that the system rests in step 3. The resulting

values of δ

are shown in Figure 7. They correspond

to that of x

at the instants of reaching l

and l

after

each commutation between these two locations. As a

result, δ

is equivalent to that of x

at any instant

during the system dynamics either in l

or l

The behavior of stopwatch y

is different from that

of x

. y

is suspended when the automaton ﬁres from

to l

. y

resumes in location l

from the same value

when it was suspended, then we associate the action

↓ δ

:= δ

+ x

to step 2 to memorize this value. δ

is initialized when the automaton resets to 0 the stop-

watch y

. The describing exactly the given part of au-

tomaton is given in Figure 6.2.

In Figure 6.1, x

and y

are initialized by ﬁring the arc

→ l

. Our grafcet does this resetting by allocating

to zero the variables δ

and δ

after the ﬁring from

step 2 to 4. The action resetting the shifting variables

will be associated to the step 4. The initial step of is

associated by an impulse action resetting all the shift-

ing variables used in the grafcet.

The grafcet monitor checks permanently the time

space associated to the actual step. The faulty step

is reached when the system violates this time range.

This fact can be represented in the grafcet model by

using the concept of hierarchy. It is easy to imagine

that a grafcet G

has an inﬂuence on anther grafcet

. G

is the Grafcet resulting from structural trans-

lation described above (Fig. 6.2). G

has two steps:

initial and faulty steps (Fig. 6.3). The activation of

initial step of G

expresses that the system’s behavior

is acceptable. G

evolves to faulty step when the time

space is violated. Let E

,..E

,..,E

be the time sub-

space in the locations l

,..,l

permitting to evolve

to the faulty state. The corresponding steps in grafcet

are 1,..,i,..,n. The receptivity of t

in Figure 6.3

is: [X

+ .. + X

]. In Figure 6.3, the

event ↑ m represents the reparation operation.

4 APPLICATION

conveyor

Sensor

Pallet

Robot

Assembly

station

-2-

()y

-1-

-3-

, xy

Alarm

0.5

1.5

()x

Figure 8: -1- Workshop -2- Working speciﬁcation -3- A sce-

nario of working.

Figure 8 shows a manufacturing system and its work-

ing speciﬁcation. In this system, when the control

system gives the order d, the actuator puts down a

pallet on the conveyor. When the sensor B detects

the transferred pallet (event b), and if the robot is not

busy (event e), it transfers the pallet to the assembly

station. The actuator comes back to its initial state and

waits again d. When the robot ﬁnishes its task (event

R), it returns to its initial state. The information con-

cerning the interruptible tasks is given in the follow-

ing table. t.u is the abbreviation for ”time units”.

Task name Conveyor task Robot task

[α

,β

] (t.u) [3,4] [2,3]

[α

,γ

) (t.u) [3,5) [2,4)

Used stopwatches x

and y

Monitoring signals s

and r

In Figure 9.1, we give the monitoring automaton of

the considered system composed of 12 locations and

focalize to a part of it in Figure 9.2. The time spaces

in the locations have been calculated by using the

model-checker PHAVer (Frehse, 2005).

Figure 8.3 shows a scenario of working where the

robot and conveyor start their tasks simultaneously.

This situation is represented by location L

as the

stopwatches dynamic’s show. In this scenario, the

conveyor is interrupted 2 t.u. Then, the system ﬁres

to L

. The inequality in bold in L

detects a fault in

the considered behavior at the instant x

(θ) = 3. The

corresponding value of y

is y

(θ) = 1. This result

can be explained as follows: to ﬁnish the conveyor

task correctly, one needs to have at least the duration

− y

(θ) = 3 − 1 = 2 t.u. The corresponding value

of x

will be x

= x

(θ) + (α

− y

(θ)) = 3 + 2 = 5.

This value exceeds the maximum permitted duration

of conveyor’s task. Figure 10.1 shows the monitoring

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

224

x1, y1

0x y 2

0x x 2

y4,x5

y3,x4

••

≤−<

≤

≤<

x1, y1

x1, y0

0x y 2

0x x 2

y4,x5

y3,x4

••

≤

−<

≤

−<

≤

−<

≤

≤<

≤

−<xy

x1, x

••

≤

0x y

≤−<

•

≤

−<

x1, y

x1, y1

••

0x y 2

0x x 2

y4,x5

y3,x4

≤

−<

≤

−<

≤

≤<

•

-1-

-2-

≤

3x x

≤

−

x1, x

••

0x y

≤

−<

•

≤

3x x

≤

−

•

Figure 9: 1- Automaton A

∗

2- Scoped part of A

∗

Figure 10: 1- G

2- Shifting and initiation actions 3- G

evolutions 4- evolution of Grafcet variables.

grafcet G

of the system. The timers T

, T

and

correspond respectively to stopwatches x

, x

, y

and y

. The used shifting variables are : δ

, δ

, and δ

. Figure 10.3 shows the evolution of

according to the proposed scenario.

The receptivity of transition t

in G

(Fig. 6.3) is:

Its predicate becomes true at the instant t = 3 because

= 1 and the inequality (δ

+ x

) −δ

≥ 2 in E

becomes true at this instant as shown in Figure 10.4.

5 CONCLUSION

Active approach has been carried out to provide solu-

tion to speciﬁc problem related to the fault detection

which is the ability to detect the faults as early as pos-

sible. It is based on a stopwatch automaton which

provides a formal support to this approach. The link

between the design of monitoring system and its im-

plementation in programmable logic controller is pro-

vided using grafcet tool. We have shown how the

grafcet can be used to describe the monitoring stop-

watch automaton’s behavior.

REFERENCES

A.allahham and alla, H. (2006). Monitoring of timed dis-

crete events systems: Application to manufacturing

systems. In The 32nd Annual conference of IEEE In-

dustrial Electronics Society.

Alur, R., Courcoubetis, C., Halbwachs, N., Henzingerd,

T., Hod, P., Nicollin, X., Olivero, A., Sifakis, J., and

Yovine, S. (1995). The algoritmic analysis of hybrid

systems. Theoretical Computer Science, 138(1).

Cassez, F. and Larsen, K. (2000). The impressive power of

stopwatch. In 11th conference on concurrency theory,

number 1877, pages 138–152.

David, R. (1995). Grafcet: A powerful tool for speciﬁcation

of logic controllers. IEEE transactions on control, sys-

tems technology, 3(3).

Frehse, G. (2005). Phaver: Algorithmic veriﬁcation of hy-

brid systems past hytech. In The Fifth International

Workshop on Hybrid Systems: Computation and Con-

trol, pages 258–273.

Ghazel, M., Togu

eni, A., and Bigang, M. (2005). A mon-

itoring approach for discrete events systems based on

a timed perti net model. In Proceedings of 16th IFAC

World Congress.

Huang, Z., Chandra, V., Jiang, S., and Kumar, R. (1996).

Modeling discrte event systems with faults using a

rules based modeling formalism. Mathematical Mod-

eling of Systems, 1(1).

S. H. ZAd, R. H. K. and Wonham, W. M. (2003). Fault

diagnosis in discrete-event systems: Framework and

model reduction. IEEE Transactions On Automatic

Control, 48(7):1199–1212.

DESIGN AND IMPLEMENTATION OF A MONITORING SYSTEM USING GRAFCET

225