
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT
ENGINE TEST BEDS
Alexander Sung, Andreas Zell
Wilhelm-Schickard-Institute for Computer Science, University of T
¨
ubingen, Sand 1, T
¨
ubingen, Germany
Florian Kl
¨
opper, Alexander Vogel
Powertrain / Testing Methods, BMW Group, Munich, Germany
Keywords:
Online Optimization, Engine Test Bed.
Abstract:
The settling times of target functions play an important role in the domain of online optimization at the engine
test bed. Inert target functions generally induce long measuring times which lead to increased costs. In this
article, we analyze how previous knowledge about the physical behavior of target functions can be used to
early predict the final steady state value to reduce measuring times.
1 INTRODUCTION
In recent years, model based algorithms have gained
significance in the domain of online optimization
of combustion engines (Isermann, 2003). In this
area, known optimization systems like, for example,
Cameo (Gschweitl et al., 2001) and Vega (Breden-
beck, 1999) are in use, but the algorithm mbminimize
presented in (Kn
¨
odler et al., 2003) (Kn
¨
odler, 2004)
(Poland et al., 2003) also has found its place in real
applications.
An important and time consuming part of online
optimization is the extraction of measuring data at the
engine test bed. Inert target functions, like e.g. the
exhaust gas temperature, need a long time until the
final steady state value of the target function – also
called target value – is reached for a certain combi-
nation of input parameters. In addition, the detec-
tion of the final value is complicated by noise. On
the other hand, the behavior of transient oscillation is
often known, or can be derived from physical rules
in order to early predict the target value. This pro-
cedure is investigated in the given contribution, first
in simulation and then on real engine data. Preced-
ing analysis like (Flohr, 2005) (Schropp, 2006) show
that the behavior of target functions in this application
domain can often be described by simple mathemat-
ical functions. A target value prediction during the
online optimization based on a small amount of data
therefore has the potential to reduce the effort of mea-
suring. The idea of prediction is not new, of course.
There is recent work like (Castillo and Melin, 2002)
(Han et al., 2004) (Teo et al., 2001) (Wang and Fu,
2005) which deals with this topic using approxima-
tors such as neural networks, genetic algorithms, or
support vector machines for predictions based on time
series.
2 TARGET VALUE PREDICTION
In this section, the algorithm of target value prediction
is presented on idealized, artificially composed mea-
suring data. In addition, the algorithm is tested with
regard to robustness against noise.
2.1 The Principle of Target Value
Prediction
The progression of target functions is often inversely
exponential. A typical example is the temperature. At
the engine test bed, the exhaust gas temperature is a
quantity, which reacts slowly to adjustments of the in-
put parameters in comparison with other quantities of
the engine. It is thereby an ideal candicate for the fol-
lowing analyses for two reasons: On the one hand, it
is easy to get a large amount of measuring data dur-
ing the time of transient oscillation due to the inertia
of the target function. On the other hand, the possible
108
Sung A., Zell A., Klöpper F. and Vogel A. (2007).
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT ENGINE TEST BEDS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 108-115
DOI: 10.5220/0001639301080115
Copyright
c
SciTePress

Figure 1: Idealized measuring data and the result of target
value prediction.
profit of time gained by using target value prediction
is especially large.
Figure 1 shows artificially generated, idealized
measuring data of a target function with such a be-
havior, displayed by the black circles. The system is
steady at the beginning and reacts with a delay to the
adjustments of the input values. The recorded data
is used as basis for online calculations by the target
value prediction. With a function approximation al-
gorithm based on least squares optimization, the be-
havior of the target function is emulated, and a target
value is predicted. So, if the data is given as
x
i
,
˜
f(x
i
)
with
˜
f being the unknown target function, the objec-
tive is to find parameter values~v = (v
1
,v
2
,v
3
) that ap-
proximate the error
E =
∑
i
v
1
· e
v
2
·x
i
+ v
3
−
˜
f(x
i
)
2
→ min! (1)
best. The result for the idealized data is also shown
in figure 1. If the data is so ideal and free of noise
like this, an early determination of the target value is
simple. A greater challenge is given by the addition
of noise, which is shown in the next section.
An important aspect of the prediction lies in the
correct detection of the moment when the target func-
tion reacts to changes of the input. This point in time
is unknown in a real application, and the response
time often varies. In our applications, this moment
is determinated by a significant change in the target
values over a longer span of time. Therefore, it is fun-
damental for our algorithm to have a continuous and
detailed record of the target function. Given the data
x
i
,
˜
f(x
i
)
, we first filter our plateaus by replacing ev-
ery set
{x
i−n
,. . ., x
i
}|∀ j ∈ {1, . .., n} :
˜
f(x
i− j
) =
˜
f(x
i
)
with its final data point x
i
discarding the rest, then we
choose the smallest x
i
from the set
x
i
|
˜
f(x
i+δ
) −
˜
f(x
i
)| > λ
max
i
˜
f(x
i
) − min
i
˜
f(x
i
)
.
δ and λ are empirically specified parameters.
During the online operation, the target value
prediction is updated constantly with additionally
recorded data. The algorithm is suited for online use,
because the calculation of the target value only re-
quires a few milliseconds. Depending on the noise,
the predicted target value often changes when new
measuring data is added, and the prediction improves
in quality with an increased amount of data. The qual-
ity of the target value prediction is compared to the
standard method, which is still in use at the test beds
at present. The standard method assumes that the tar-
get function is tuned after a fixed amount of waiting
time, specified in advance. Then, an averaged mea-
suring value is used as final target value. In our sim-
ulation the waiting time, also referred to as stationary
time, is set to the point in time when the target func-
tion has reached 95% of its final value. At this point, a
measuring time of half the stationary time’s duration
is used. This is in accordance to the situation at the
engine test bed.
2.2 The Inpact of Noise
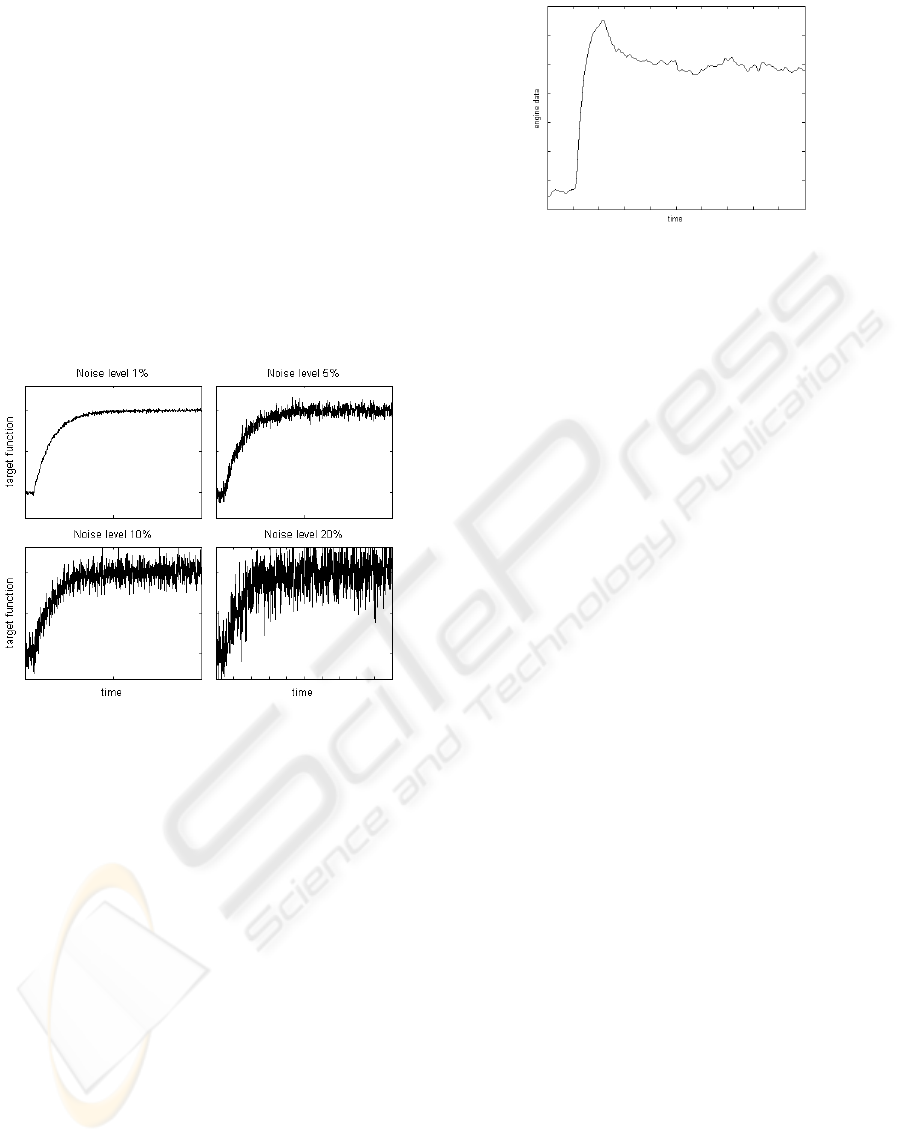
To test the robustness of the algorithm against noise,
the following tests were done. For different noise
levels 1000 test runs were evaluated each. Normal
distributed noise was used with a standard deviation
specified in relation to the range of the target values.
The results are the averaged saving of time in com-
parison to the standard method with a fixed station-
ary time, as well as the relative error reduction ε, cal-
culated as the fraction of error ε
Ref
of the standard
method by which the prediction error ε
Pred
is lower,
and vice versa:
ε =
(
ε
Ref
−ε
Pred
ε
Ref
if ε
Pred
< ε
Ref
ε
Ref
−ε
Pred
ε
Pred
otherwise
. (2)
The higher the values are, the better target value pre-
diction worked. The prediction success displays how
often the prediction error was smaller than the error
of the standard method. The results are presented in
table 1.
Table 1: Investigation of noise influence.
Noise
Saving Error Prediction
level
of time reduction success
1% 46.1% 68.4% 96.6%
2%
42.7% 42.6% 80.1%
3%
39.3% 26.6% 68.4%
5%
33.9% 7.5% 55.9%
10%
23.2% 0.0% 46.6%
By means of these results, it was possible to con-
firm the assumption that the function approximation
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT ENGINE TEST BEDS
109
method of the target value prediction is able to deter-
mine the final value more precisely than a simple av-
eraging after a fixed stationary time. With increased
noise, which significantly falsifies the measuring data
especially in the early phase of transient oscillation,
the difference lessens because an early prediction is
not possible anymore in this case.
At a high noise level, which may commonly occur
in real applications, an early prediction is still possi-
ble, but the success is lacking. In the next section,
we show how this trade-off can be used to reduce the
overall measuring time of an optimization problem
without downgrading the final results.
Figure 2 shows sample data sets with different
noise levels.
Figure 2: Sample data with different noise levels.
2.3 Addressing More Than Simple
E-functions
The simple E-function is only one of different pos-
sibilities to describe the behavior of target functions.
In our real application, for example, we found that a
twofold E-function v
1
· e
v
2
·x
i
+ v
3
· e
v
4
·x
i
+ v
5
was bet-
ter suited to describe the progression of the measuring
data. This and other unexpected behavior in the data
may be explained by the measuring technology, the
interplay of which still needs more investigations. In
this contribution, we want to mention two examples,
which occur commonly at the engine test bed.
Figure 3 shows an example of real engine data
with an overshooting behavior. In this case, the tar-
get values react to changes of the input parameters by
progressing past the final steady state value first, and
then continue retrogressive afterwards. The difficulty
lies in the fact that the overshooting behavior cannot
be detected before the retrogressive part is recorded.
Figure 3: An example of real engine data with overshooting
behavior.
An early target value prediction will therefore fail to
describe the progession correctly. For an optimiza-
tion problem with several measuring points, the deci-
sion whether to abort the measuring process due to an
early target value prediction can be made depending
on the significance of the expected target value. For
example, if the current target value is already under
a certain threshold of importance and the predicted
value has even less impact on the optimization result,
a possible overshooting can be neglected.
Sometimes, a drift in the target values can be
detected. This behavior can be identified with tar-
get value predictions, too. If several predictions are
recorded over a longer period of time, it becomes ev-
ident that a small linear time is included in the under-
lying target function v
1
·e
v
2
·x
i
+v
3
·x
i
+v
4
. In general,
however, the influence of drift at one single measuring
point is too small to have a significant impact on the
final steady state value. Since the detection of drift be-
havior is complicated by noise and requires a longer
period of measuring time, we neglect the possible oc-
currence of drift in general. This corresponds to the
standard measuring method, which determines the fi-
nal result as an averaged measuring value.
3 RESULTS IN REAL
APPLICATIONS
This section consists of several applications from the
domains of both simulation and the engine test bed,
in which target value prediction improves the final re-
sults.
3.1 Model-based Optimization
In the applications of this section, we used a model-
based approach for the optimization of the input pa-
rameters of a target function that was defined over a
given input space. The models of the target function
were generated by a committee of neural networks
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
110
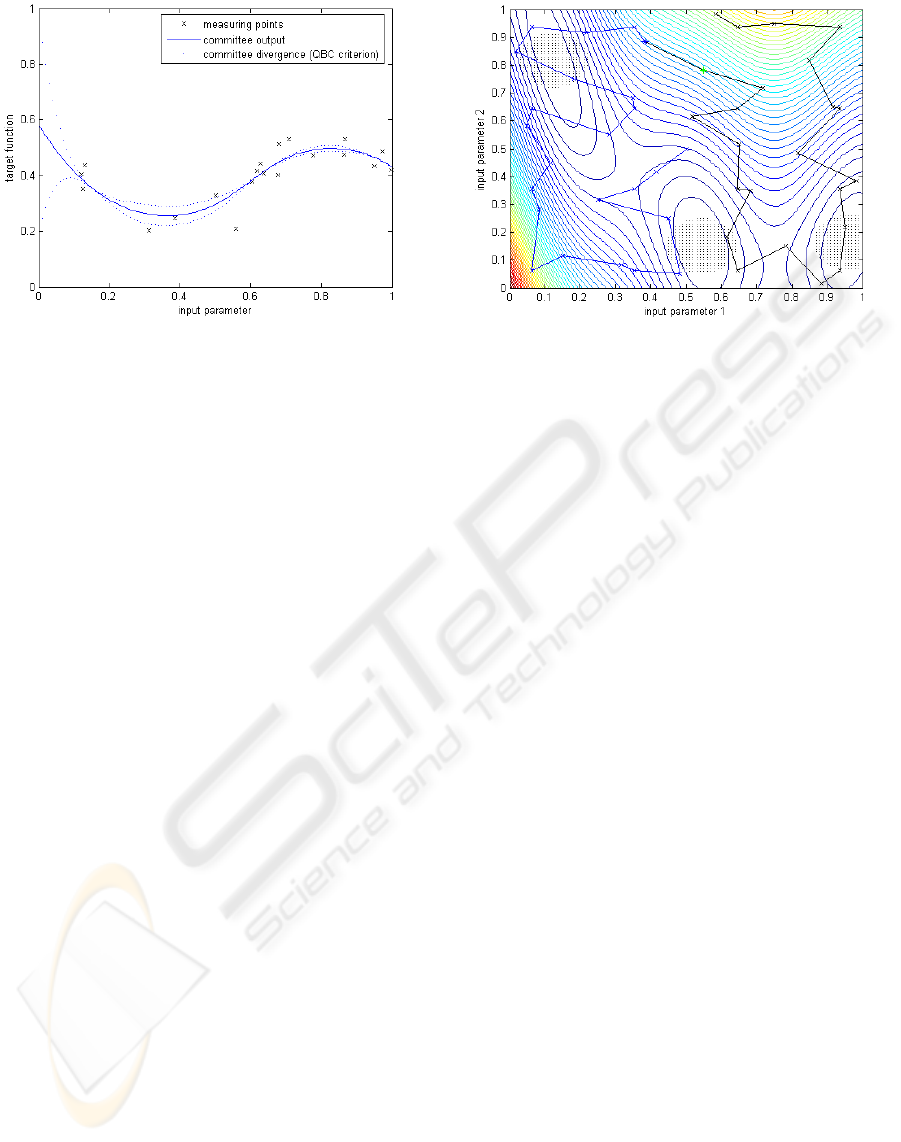
Figure 4: Model output of a committee of neural networks
and linear regression. The QBC criterion is a measurement
for the uncertainty and supplies the largest values to the
points where the committee’s individual models diverge the
most.
and LLR models, the output of the later being a lin-
ear combination of non-linear basic functions. Neural
networks have been long established in model-based
optimization, as illustrated in (Hafner, 2002) (Hafner
et al., 2000) (Sch
¨
uler et al., 2000), for example. The
strengths of neural networks for our use lies in the
ability to produce a good overall approximation of the
target function based on few data points without prior
knowledge. The LLR models, on the other hand, are
designed to specifically describe local behavior in the
input space in detail.
Based on such a model, we calculate a QBC crite-
rion (query by committee), of which figure 4 provides
an example over an one-dimensional input space. The
QBC criterion supplies the largest values to the points
where the committee’s individual models diverge the
most. The information of already known measuring
points is included to avoid repeated measuring at the
same input values. The expression ”query” here de-
notes the decision-making process to determine the
next measuring point with the aid of the currently
available model. This method will be used in the fol-
lowing subsection.
3.2 Optimization in a Simulation
Environment
As a first application, we used our algorithm in a
simulation environment, which was designed for the
optimization of an engine model. Measuring points
were chosen in a two-dimensional search space by a
D-optimal DoE-method (R
¨
opke, 2005) (Weber et al.,
2005). The goal was to find the local minima and
to model the regions around them with the least er-
ror possible. We used the Branin function as the tar-
Figure 5: Snapshot of the online optimization in a simula-
tion environment. The black dots mark the test error set.
get function and simulated it to be inert, according to
what was described in the section before. Note, that
the test set consisted of test points near the local min-
ima only, in order to display the optimization goal.
Figure 5 shows the setup of the experiments. Our al-
gorithm was tested against the standard method with
fixed stationary and measuring time.
There are two conditions, after which the predic-
tion based algorithm completes the measuring process
at a specific measuring point and evaluates the gath-
ered measuring data via prediction: In the standard
case, analogous to the section before, the measuring
process is finished when the predicted value is stable
over a certain period of time. This is calculated with
the term
mean
p(t −δ), .. . , p(t − 1)
− p(t)
< α
∧ std
p(t −δ), .. . , p(t − 1)
< α (3)
using the predicted values p(t) after normalization.
The parameters δ = 30 (seconds) and α = 0.01 are
empirically determined based on real engine data.
In addition, however, there is a possibility to abort
the measuring when the expected target value is too
high to be a local minimum. In this case, the value
predicted at that moment is used as an estimated tar-
get value, even if it is to be expected that the error at
this point is quite large. The intention of this method
is to save measuring time at unimportant measuring
points to gain a first rough engine model und use the
saved time to explore the regions of minima in detail.
Figure 6 shows two cases where the measuring pro-
cess was completed due to early predictions. In the
first case, the measuring was complete since the pre-
dicted values leveled off at the point in time marked
by the dotted line. The second case shows an exam-
ple where the expected value was considered irrele-
vant for the minimization problem. The measuring
process was aborted in this case.
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT ENGINE TEST BEDS
111
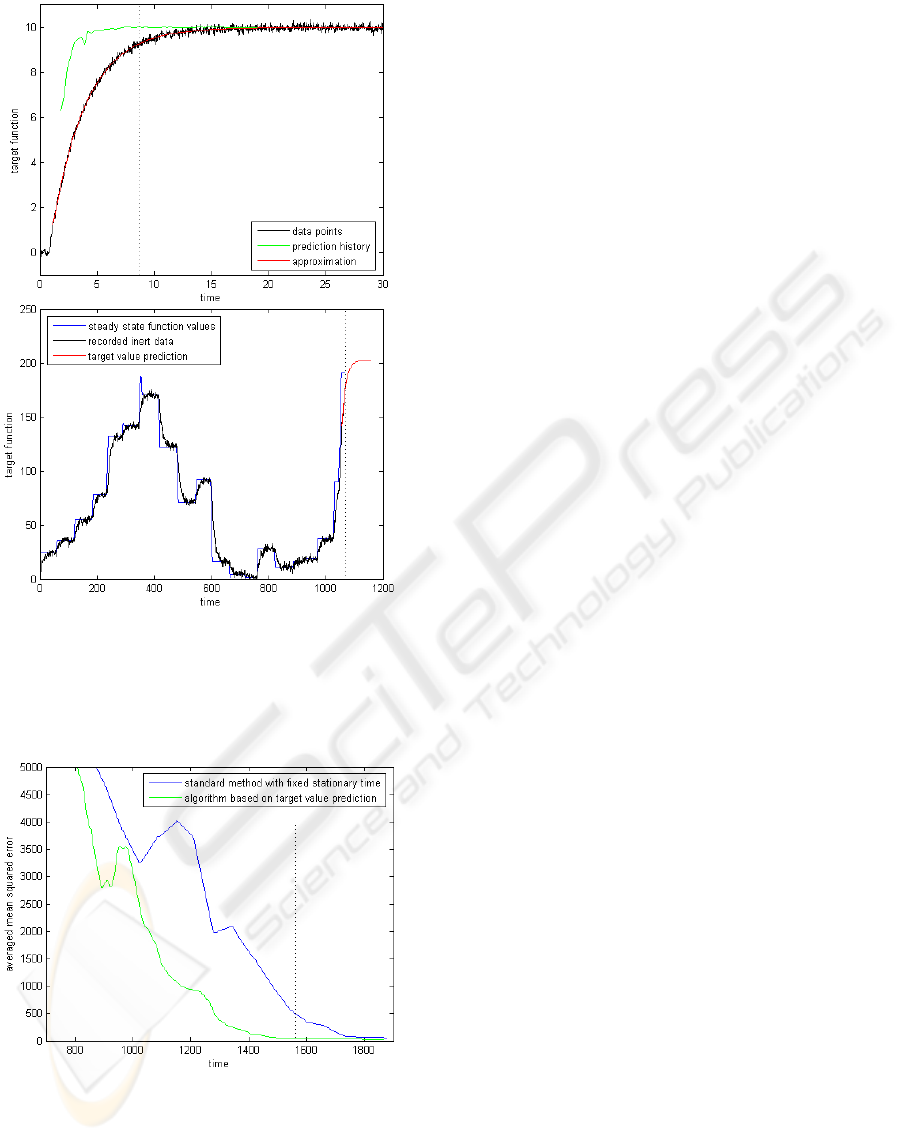
Figure 6: Examples of measuring processes completed due
to the evaluations of predicted values. In the first example,
the prediction is considered reliable, in the second exam-
ple, the expected value is considered umimportant for the
optimization.
Figure 7: Test error progression of the online optimiza-
tion in a simulation environment. The standard method is
displayed in blue, the target value prediction algorithm is
shown in green. The dotted line shows when the target value
prediction algorithm completed the initial set of data points.
Two additional rules proved to be useful for the
optimization. Measurings with target values near the
expected optimum will not be aborted, and measur-
ings near local minima based on the current, incom-
plete model will also not be aborted. The thresholds
for these options are set by the user based on rough
previous knowledge at this time, but they are not sen-
sitive. These rules grant an additional certainty that
no information will be lost unnecessarily.
Figure 7 shows the progression of the test error
during the optimization over time, as an average over
72 test runs. After 74.4% of the time that the standard
method needed in total, the target value prediction al-
gorithm evaluated the initial set of measuring points.
At that point, our algorithm created a function model
with a test error of 41.6, while the model of the stan-
dard method still had a test error of 502.6. The reason
for this huge difference lies in the fact that the stan-
dard method did not yet deal with several measuring
points, so the error near those is still very large, of
course. The final test error of the standard method
was 31.4.
In addition to the initial set of measuring points,
the prediction based algorithm used the saved time
to measure additional data points. To generate these
points, the current model of the target function was
used to locate the regions near local minima, as ex-
plained in the subsection before. Based on QBC cri-
terion, the additional measuring points were chosen
by a line search algorithm. With the additional data
points, the final test error could be reduced to 17.7
with a 43.6% improvement in comparison with the
standard method.
In this scenario, our algorithm was able to produce
a rough interim result in a shorter time. On the other
hand, using the complete amount of time available,
our algorithm was able to improve the final results in
comparison with the standard method.
3.3 Target Value Prediction on Real
Engine Data
As an example with real application data, the target
value prediction algorithm was used on engine data,
which was provided by the BMW Group in Munich.
The data consists of exhaust gas measurings and de-
scribe load step responses. The range of values has
been scaled to make the relative error values compa-
rable. The results contain 126 data sets.
Dealing with real engine data poses a problem,
which makes a presentation of the results according
to simulation difficult: The real final values of the
target function are unknown. Even after measuring
for minutes, it is possible that the transient oscillation
of several target functions still have not finished. An
open-ended measuring is not viable, however. Figure
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
112

Figure 8: Examples of recorded engine data, which still
have not reached their final values at the end of the record-
ing. The plateaus are a phenomenon of the measuring tech-
nology at the engine test bed. For comparison, the predicted
target value is included as a dotted line.
8 shows several examples of recorded engine data,
which still have not reached their final values at the
end of the recording. Plateaus in the recorded data
arise because the measuring process is disabled dur-
ing the time of evaluating and saving the engine data
at the engine test bed. The data points after this point
in time still vary, however. Therefore, additional as-
sumptions, which are derived from the simulation, are
made for the following data evaluations.
In the practice of test bed operations, target func-
tions are assumed to have reached their final values
after a certain amount of stationary time. A conclus-
ing averaged value is then accepted as target value.
In the given data, the stationary time has been set to
60 seconds. Afterwards, a measuring has been per-
formed over a timespan of 30 seconds, after which
the averaged value has been calculated. This value
was used for comparisons to rate the target value pre-
diction algorithm. The results from simulation show
that with an appropriate modeling of the target func-
tion progression given, the target value can be esti-
mated more precisely by a corresponding prediction
than by an averaged measuring value. For this reason
we assume that, in the case of real engine data, the
predicted target value, which was calculated based on
all available measuring data, approximates the real fi-
nal value best. The examples in figure 8 include the
final predicted target value for comparison. With re-
gard to this value, the results can be illustrated as in
table 2.
In the first column, a maximum error level is
given. The second column shows in how many cases
this error level was reached. The error level was
reached when the difference of the prediction result
to the expected final value did not exceed the given
Table 2: Evaluation of error levels using target value pre-
diction.
Maximum
Threshold Saving
error
success of time
3% 14.3% 21.4%
5%
27.0% 25.1%
10%
63.5% 38.4%
level for at least 10 seconds. The difference is again
calculated in relation to the range of the target func-
tion. In the last column, the averaged amount of time
is shown that could be saved in those cases where the
error level was reached. The results for the compari-
son with the standard method in analogy to simulation
are a saving of time of 26.4% and an error reduction
of 3.3%. The prediction thereby gave a better result
in 52.4% of the tests.
Figure 9: Successful target value prediction (red line) ap-
plied on real engine data (black line). Only the first part on
the left side of the dotted line was used for the prediction.
The real target value progression is shown for comparison.
Figure 9 shows an exemplary and successful target
value prediction based on engine data. In this case, a
similarity to the simulated E-function is identificable.
The complete engine data is drawn in black, while the
green dashed line highlights what data was available
to the prediction algorithm. The predicted behavior is
shown in red.
3.4 Model-based Optimization of a
Combustion Engine
As another application, we modeled a target function
of an engine over a two-dimensional parameter space.
The problem we had hereby was that there was not
enough real engine data available for an additional
large, independet test set. So, to evaluate the algo-
rithms on the real application, we had to create a sim-
ulated reference. We did this by creating an engine
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT ENGINE TEST BEDS
113
model with the given engine data. This served as a
basis for calculations about test errors.
In analogy to the subsection before, we wanted
to explore the input space by measuring certain data
points. The target values were real engine data, and
therefore the measuring process was inert. With the
acquired data, a model was created both for our algo-
rithm based on target value prediction as well as for
the standard method using stationary and measuring
times. The goal was to find the local minima with a
good representation of their immediate environments.
Note that we are refering to three different models
now. The first one is created with steady state val-
ues and serves as reference. The other two models
are calculated during the optimization process where
recorded engine data on the inert target function is
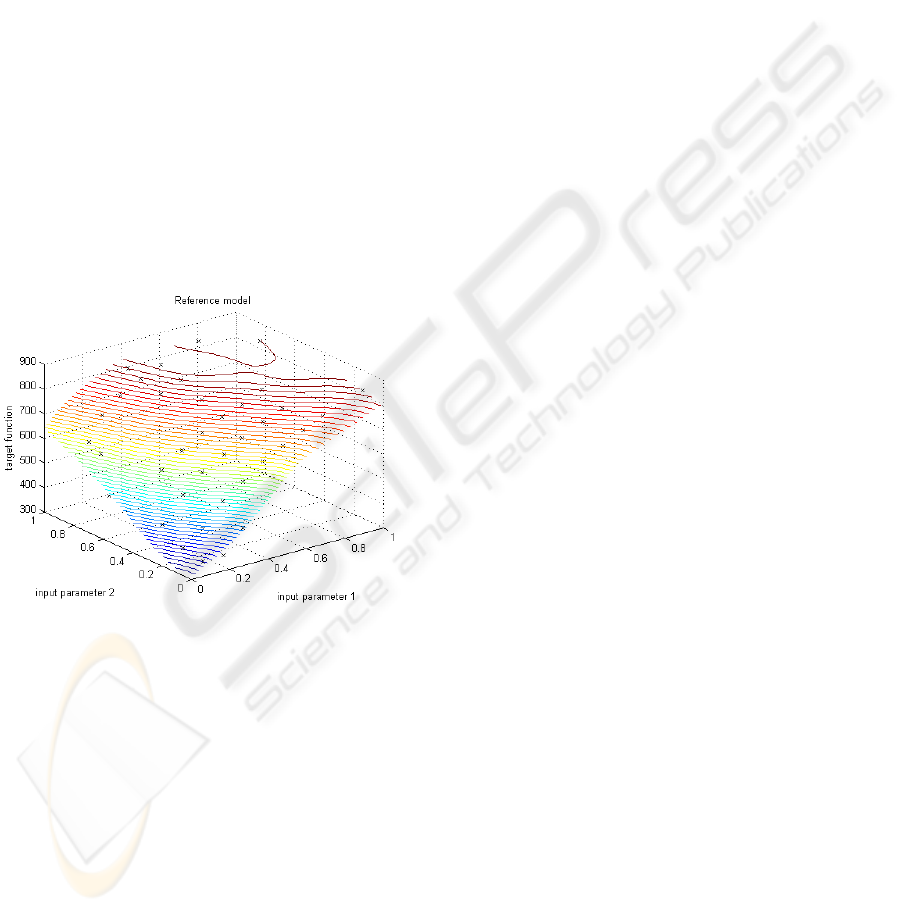
evaluated. Figure 10 shows the first of these models
which represents the engine’s target function in steady
states. Another fourth model is created by using tar-
get value prediction without the goal to minimize op-
timization time, but to achieve best test error values
instead.
Figure 10: Model of the target function based on real engine
data, and the real measuring data. The function values from
this model are used as reference in our tests.
The measuring process consisted of approach-
ing and measuring 38 data points. Using the stan-
dard method, the final mean squared error was 231.1.
The algorithm using target value prediction was able
to reach an error of 147.4 after 75.2% of the time
which the standard method needed, an improvement
of 36.8% in comparison to the standard method.
Therefore, the target value prediction could be used
to save time to early generate an engine model that
had a lower test error based on the reference model.
Furthermore, the predictions can also be done using
the same amount of time which the standard method
uses. In this variation the final result was 139.3, an
improvement of 39.7%.
4 CONCLUSION AND
PROSPECTS
In this article we described the idea and methodology
of target value prediction. Thereby, the fundamental
assumption was that the behavior of the target func-
tion after adjusting the input parameters can be de-
scribed with inversely exponential E-functions. Re-
sults from both simulation and practice show the pos-
sible success of this algorithm. We demonstrated that
the strength of the target value prediction does not lie
in single measurings, since there is always some sort
of trade-off between saving of time and precision loss
included. Given a larger scope of an entire optimiza-
tion problem, however, exactly this trade-off can be
used to concentrate available resources to the impor-
tant parts of the problem and to save valuable time at
less significant aspects.
Due to the nature of the prediction method to de-
tect the important regions of an optimization prob-
lem, we expect the algorithm to scale well with larger
problems where the areas of solutions do not scale ac-
cordingly at all. Further work will apply the proposed
method to other problems in the domain of online op-
timization and continue to show its capacity.
REFERENCES
Bredenbeck, J. (1999). Statistische Versuchsplanung
f
¨
ur die Online-Optimierung von Verbrennungs-
motoren. In MTZ-Motortechnische Zeitschrift und
MTZ-Worldwide, 60 (11). MTZ Press.
Castillo, O. and Melin, P. (2002). Hybrid intelligent sys-
tems for time series prediction using neural networks,
fuzzy logic, and fractal theory. In IEEE Transactions
on Neural Networks, 13 no. 6, pages 1395–1408.
Flohr, A. (2005). Konzept und Umsetzung einer Online-
Messdatendiagnose an Motorpr
¨
ufst
¨
anden. PhD the-
sis, University of Technology Darmstadt.
Gschweitl, K., Pfluegl, H., Fortuna, T., and Leith-
goeb, R. (2001). Steigerung der Effizienz in
der modellbasierten Motorenapplikation durch die
neue CAMEO Online DoE-Toolbox. In ATZ-
Automobiltechnische Zeitschrift und ATZ-Worldwide,
page 103 (7/8). MTZ Press.
Hafner, M. (2002). Modellbasierte station
¨
are und dynami-
sche Optimierung von Verbrennungsmotoren am Mo-
torenpr
¨
ufstand unter Verwendung neuronaler Netze.
PhD thesis, University of Technology Darmstadt.
Hafner, M., Sch
¨
uler, M., and Isermann, R. (2000). Ein-
satz schneller neuronaler Netze zur modellbasierten
Optimierung von Verbrennungsmotoren - Teil 2: Sta-
tion
¨
are und dynamische Optimierung von Verbrauch
und Emissionen. In Motortechnische Zeitschrift
(MTZ), 61 no. 11. MTZ Press.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
114

Han, M., Xi, J., Xu, S., and Yin, F.-L. (2004). Prediction
of chaotic time series based on the recurrent predic-
tor neural network. In IEEE Transactions on Signal
Processing, 52 no. 12, pages 3409–3416.
Isermann, R. (2003). Modellgest
¨
utzte Steuerung, Regelung
und Diagnose von Verbrennungsmotoren. Springer-
Verlag.
Kn
¨
odler, K. (2004). Methoden der restringierten Online-
Optimierung zur Basisapplikation moderner Verbren-
nungsmotoren. PhD thesis, University of T
¨
ubingen.
Kn
¨
odler, K., Poland, J., Zell, A., Fleischhauer, T., Mitterer,
A., and Ullmann, S. (2003). Model-based online opti-
mization of modern internal combustion engines, part
2: Limits of the feasible search space. In MTZ World-
wide (Motortechnische Zeitschrift), 64 no. 6, pages
30–32, German edition 520–526. MTZ Press.
Poland, J., Kn
¨
odler, K., Zell, A., Fleischhauer, T., Mitterer,
A., and Ullmann, S. (2003). Model-based online opti-
mization of modern internal combustion engines, part
1: Active learning. In MTZ Worldwide (Motortech-
nische Zeitschrift), 64 no. 5, pages 31–33, (German
edition: 432–437). MTZ Press.
R
¨
opke, K. (2005). DoE – Design of Experiments. In Meth-
oden und Anwendungen in der Motorenentwicklung.
verlag moderne industrie.
Schropp, S. (2006). Optimization of measurement data log-
ging at engine test benches. Master’s thesis, Univer-
sity of Technology Munich.
Sch
¨
uler, M., Hafner, M., and Isermann, R. (2000). Einsatz
schneller neuronaler Netze zur modellbasierten Op-
timierung von Verbrennungsmotoren - Teil 1: Mod-
ellbildung des Motor- und Abgasverhaltens. In Mo-
tortechnische Zeitschrift (MTZ), 61 no. 10. MTZ
Press.
Teo, K. K., Wang, L., and Lin, Z. (2001). Wavelet packet
multi-layer perceptron for chaotic time series predic-
tion: Effects of weight initialization. In Lecture Notes
in Computer Science, Vol. 2074, pages 310–317.
Wang, L. and Fu, X. (2005). Data mining with computa-
tional intelligence. In IEEE Transactions on Neural
Networks, 17 no. 3. Springer.
Weber, M., K
¨
otter, H., Schreiber, A., and Isermann, R.
(2005). Model-based Design of Experiments for Static
and Dynamic Measurements of Combustion Engines.
In 3. Tagung: Design of Experiments (DoE) in der
Motorenentwicklung, Berlin.
TARGET VALUE PREDICTION FOR ONLINE OPTIMIZATION AT ENGINE TEST BEDS
115
