
DETECTION OF THE NEED FOR A MODEL UPDATE IN STEEL
MANUFACTURING
Heli Koskim
¨
aki (n
´
ee Junno), Ilmari Juutilainen, Perttu Laurinen and Juha R
¨
oning
Intelligent Systems Group, University of Oulu, PO BOX 4500,90014 University of Oulu, Finland
Keywords:
Adaptive model update, similar past cases, error in neighborhood, process data.
Abstract:
When new data are obtained or simply when time goes by, the prediction accuracy of models in use may
decrease. However, the question is when prediction accuracy has dropped to a level where the model can
be considered out of date and in need of updating. This article describes a method that was developed for
detecting the need for a model update. The method is applied in the steel industry, and the model whose need
of updating is under study is a regression model developed to model the yield strength of steel plates. It is used
to plan process settings in steel plate product manufacturing. To decide on the need for updating, information
from similar past cases was utilized by introducing a limit called an exception limit. The limit was used to
indicate when a new observation was from an area of the model input space where the prediction errors of the
model have been too high. Moreover, an additional limit was formed to indicate when too many exceedings of
the exception limit have occurred within a certain time scale. These two limits were then used to decide when
to update the model.
1 INTRODUCTION
At the Ruukki’s steel works in Raahe, Finland, liq-
uid steel is cast into steel slabs that are then rolled
into steel plates. Many different variables and mech-
anisms affect the mechanical properties of the final
steel plates. The desired specifications of the me-
chanical properties of the plates vary, and to fulfill
the specifications, different treatments are required.
Some of these treatments are complicated and ex-
pensive, so it is possible to optimize the process by
predicting the mechanical properties beforehand on
the basis of planned production settings (Khattree and
Rao, 2003).
Regression models have been developed for
Ruukki to help development engineers control me-
chanical properties such as yield strength, tensile
strength, and elongation of the metal plates (Juuti-
lainen and R
¨
oning, 2006). However, acquirement of
new data and the passing of time decrease the reliabil-
ity of the models, which can bring economical losses
to the plant. For example, when mechanical proper-
ties required by the customer are not satisfied in qual-
ification tests, the testing lot in question need to be re-
produced. If also retesting gives unsatisfactory result
the whole order has to be produced again. Because of
the volumes produced in a steel mill, this can cause
huge losses. Thus, updating of the models emerges as
an important step in improving modelling in the long
run. This study concerns the need to update the re-
gression model developed to model the yield strength
of steel plates.
In practice, because the model is used in ad-
vance to plan process settings and since the employ-
ees know well how to produce common steel plate
products, modelling of rare and new events becomes
the most important aspect. However, to make new
or rarely manufactured products, a reliable model is
needed. Thus, when comparing the improvement in
the model’s performance, rare events are emphasized.
In this study, model adaptation is approached by
searching for the exact time when the performance
of the model has decreased too much. In practice,
model adaptation means retraining the model at opti-
mally selected intervals. However, because the sys-
tem has to adapt quickly to a new situation in order to
55
Koskimäki (née Junno) H., Juutilainen I., Laurinen P. and Röning J. (2007).
DETECTION OF THE NEED FOR A MODEL UPDATE IN STEEL MANUFACTURING.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 55-59
DOI: 10.5220/0001639500550059
Copyright
c
SciTePress

avoid losses to the plant, periodic retraining, used in
many methods ((Haykin, 1999), (Yang et al., 2004)),
is not considered the best approach. Moreover, there
are also disadvantages if retraining is done unneces-
sarily. For example, extra work is needed to take a
new model into use in the actual application environ-
ment. In the worst case, this can result in coding er-
rors that affect the actual accuracy of the model.
Some other studies, for example (Gabrys et al.,
2005), have considered model adaptation as the
model’s ability to learn behavior in areas from which
information has not been acquired. In this study,
adaptation of the model is considered to be the ability
to react to time-dependent changes in the modelled
causality. In spite of extensive literature searches,
studies that would be comparable with the approach
used in this article were not found. Thus, it can be
assumed that the approach is new, at least in an actual
industrial application.
2 DATA SET AND REGRESSION
MODEL
The data for this study were collected from the
Ruukki’s steel works production database between
July 2001 and April 2006. The whole data set con-
sisted of approximately 250,000 observations. In-
formation was gathered from element concentrations
of actual ladle analyses, normalization indicators,
rolling variables, steel plate thicknesses, and other
process-related variables (Juutilainen et al., 2003).
The observations were gathered during actual product
manufacturing. The volumes of the products varied,
but if there were more than 500 observations from one
product, the product was considered a common prod-
uct. Products with less than 50 observations were cat-
egorized as rare products.
The response variable used in the regression mod-
elling was the Box-Cox-transformed yield strength of
the steel plates. The Box-Cox transformation was se-
lected to produce a Gaussian-distributed error term.
The studied regression model was a link-linear model
y
i
= µ
i
+ ε
i
, where µ
i
= f(x
i
β) and ε
i
are indepen-
dently distributed Gaussian errors. The length of the
parameter vector β was 130. In addition to 30 orig-
inal input variables, the input vector x
i
included 100
carefully chosen non-linear transformations of origi-
nal input variables; for example, many of these trans-
formations were products of two or three original in-
puts. The results are presented in the original (non-
transformed) scale of the response variable.
3 NEIGHBORHOOD AND APEN
In this study the need for a model update was
approached using information from previous cases,
namely the average prediction errors of similar past
cases. Thus, for every new observation, a neighbor-
hood containing similar past cases was formed and an
average prediction error inside the neighborhood was
calculated.
The neighborhoods were defined using a Euclid-
ian distance measure and the distance calculation was
done only for previous observations to resemble the
actual operating environment. The input variables
were weighted using gradient-based scaling, so the
weighting was relative to the importance of the vari-
ables in regression model (Juutilainen and R
¨
oning,
ress). A numerical value of 3.5 was considered for
the maximum distance inside which the neighboring
observations were selected. The value was selected
using prior knowledge of the input variable values.
Thus, a significant difference in certain variable val-
ues with the defined weighting resulted in Euclidean
distances of over 3.5. In addition to this, the maxi-
mum count of the selected neighbors was restricted to
500.
After the neighborhood for a new observation was
defined, the average prediction error of the neigh-
borhood (= APEN) was calculated as the distance-
weighted mean of the prediction errors of observa-
tions belonging to the neighborhood:
APEN =
∑
n
i=1
[(1−
d
i
max(d)
) ·
b
ε
i
]
∑
n
i=1
(1−
d
i
max(d)
)
, (1)
where
n = number of observations in a neighbor-
hood,
ε(i) = the prediction error of ith observation
of the neighborhood,
d
i
= the Euclidian distance from the new
observation to ith observation of the
neighborhood,
max(d) = the maximum allowed Euclidian dis-
tance between the new observation
and the previous observations in the
neighborhood (= 3.5).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
56

4 STUDY
The method used to observe the need for a model up-
date was to determine when the model’s average pre-
diction error in the neighborhood of a new observa-
tion (APEN) differed from zero too much compared
with the amount of similar past cases. When there are
plenty of accurately predicted similar past cases, the
APEN is always near zero. When the amount of sim-
ilar past cases decreases, the sensitivity of the APEN
(in relation to measurement variation) increases, also
in situations when the actual model would be accu-
rate. In other words, the relationship between the
sensitivity of the APEN and the number of neighbors
is negatively correlated. The actual updating is also
time-dependent, which means the model is updated
when too many observations have an APEN value that
differs significantly from zero within a certain time
interval.
A limit, called the exception limit, was introduced
to detect the need to update the model. The limit de-
fines how high the absolute value of the average pre-
diction error of a neighborhood (= |APEN|) has to
be in relation to the size of the neighborhood before
it can be considered an exception. This design was
introduced to avoid possible sensitivity issues of the
APEN. In practice, if the size of the neighborhood
was 500 (the area is well known), prediction errors
higher than 8 were defined as exceptions, while with
a neighborhood whose size was 5, the error had to be
over 50. The values of the prediction errors used were
decided by relating them to the average predicted de-
viation,
¯
ˆ
σ
i
(≈ 14.4). The predicted deviations were
acquired by using a regression model (Juutilainen and
R
¨
oning, 2006). The limit is shown in Figure 1.
0 50 100 150 200 250 300 350 400 450 500
5
10
15
20
25
30
35
40
45
50
55
Size of neighborhood
Average estimation error
Figure 1: Exception limit.
A second limit, the update limit, was defined as
being exceeded if 10 percent of the average predic-
tion errors of the neighborhoods within a certain time
interval exceeded the exception limit. The chosen in-
terval was 1000 observations, which represents mea-
surements from approximately one week of produc-
tion. Thus, the model was retrained every time 100 of
the preceding 1000 observations exceeded the excep-
tion limit.
The study was started by training the parameters
of the regression model using the first 50,000 observa-
tions (approximately one year). After that the trained
model was used to give the APENs of new observa-
tions. The point where the update limit was exceeded
the first time was located and the parameters of the
model were updated using all the data acquired by
then. The study was carried on by studying the relia-
bility of the model after each update and repeating the
steps iteratively until the whole data set was passed.
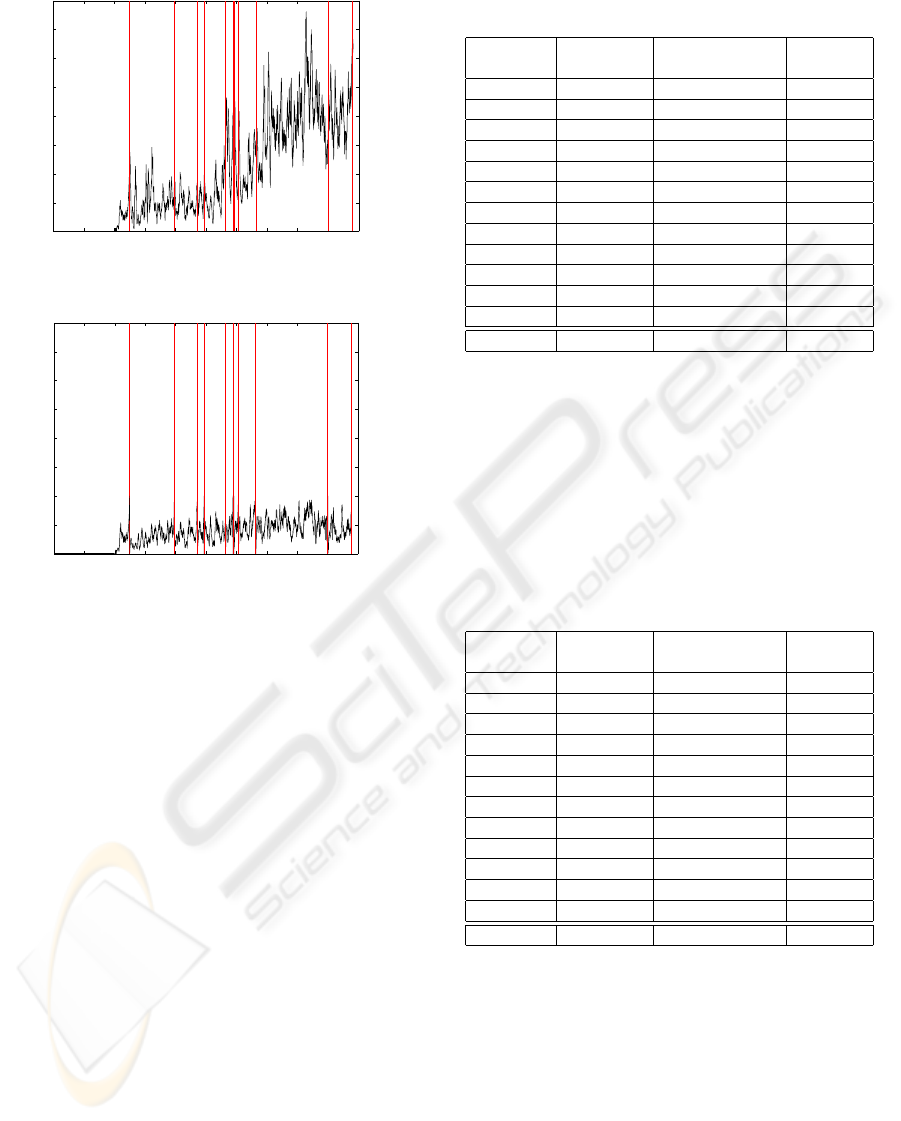
5 RESULTS
First the reliability of the model with and without up-
dating was studied. Figure 2 shows the average pre-
diction errors of the respective neighborhoods. Fig-
ure 2(a) shows the model’s performance without up-
dating. The straight line in the beginning represents
the training data and the rest of the curve shows the
proportional share of the exceedings of the exception
limit, in other words, the percentage of APENs that
exceeded the exception limit. For example, it can be
seen that at the end of the curve the APEN of every
fourth new observation per week has exceeded the ex-
ception limit. The vertical lines mark the points of
iteration where the update limit has been exceeded.
On the other hand, Figure 2(b) presents the reliability
of the model when the parameters are re-estimated at
times indicated by the vertical lines. The curve repre-
sents the error rate of the re-trained model.
The positive effect of the updates on the average
prediction errors of the neighborhoods can be clearly
seen from Figure 2. Therefore, it is evident that the
model’s performance increases when the developed
updating strategy is applied.
Although the reliability information of the model
is very useful, the effect of the update on the actual
prediction error was considered more important. Two
different goodness criteria were used to compare the
actual prediction errors of the updated models. Both
criteria emphasize rare events, because that is the case
when the model is needed the most. Both of them
show the weighted average of the absolute prediction
errors, with different weighting schemes.
In the first goodness criterion the idea is to em-
phasize all the products by approximately an equal
amount. This means that in the calculation of the
average prediction error, the weights of observations
DETECTION OF THE NEED FOR A MODEL UPDATE IN STEEL MANUFACTURING
57
0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5
x 10
5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
The observation number
The proportional share of deviations (window size 1000)
(a) Without update.
0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.52.5
x 10
5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
The observation number
The proportional share of deviations (window size 1000)
(b) With update.
Figure 2: Reliability of the model.
belonging to products having more than 50 observa-
tions are decreased. The results of the goodness cri-
terion are shown in Table 1. The step size indicates
the length of the iteration step (comparable with the
space between the vertical lines in Figure 2). The re-
sults are averages of the absolute prediction errors of
the observations between each iteration step. Thus,
the size of the data set used to calculate the average
is the same as the step size. In addition to this, to
compare the results, the prediction error averages are
presented in three different cases: predicted with a
newly updated model, with a model updated in the
previous iteration step, and with a model that was not
updated at all. The results show that, although the dif-
ferences between the new model and the model from
the previous iteration step are not big, the update im-
proves the prediction in each of the steps. The benefit
of the model update is obvious when the results of the
updated model and the model without an update are
compared.
The second goodness criterion was formed to take
only rare events into account. Thus, only the cases
Table 1: Means of absolute prediction errors with the first
goodness criterion.
Step size With new With previous Without
model model update
12228 - - -
36812 11.59 11.74 11.74
18826 10.47 11.00 10.69
5623 10.93 11.08 11.25
17636 12.48 12.57 12.97
6165 11.48 12.38 13.31
699 29.92 30.20 41.00
3765 11.79 12.21 13.96
14317 12.35 12.42 13.53
59432 12.22 12.39 12.87
19455 12.72 13.46 14.81
507 11.46 11.68 15.22
mean 12.07 12.32 12.79
where the neighborhood size is smaller than 50 are
considered. The absolute prediction errors of these
rare observations affect the average equal amount.
The update proves its functionality in this scheme,
also. The prediction errors are notably smaller when
the model is updated (see Table 2).
Table 2: Means of absolute prediction errors with the sec-
ond goodness criterion.
Step size With new With previous Without
model model update
12228 - - -
36812 14.41 14.63 14.63
18826 13.14 14.12 13.99
5623 12.94 13.11 13.10
17636 16.48 16.60 18.22
6165 12.60 13.90 14.71
699 84.86 85.86 115.44
3765 13.88 17.08 21.28
14317 16.23 16.21 22.09
59432 15.42 15.54 17.90
19455 26.42 27.88 43.87
507 15.99 15.18 16.04
mean 15.67 16.04 18.10
With this data set, determination of the need for
a model update and the actual update process proved
their efficiency. The number of iteration steps seems
to be quite large, but like in Figure 2, the iteration
steps get longer when more data is used to train the
model. Thus, the amount of updates decreases as time
goes on. However, the developed approach can also
adapt to changes rapidly, when needed, as when new
products are introduced or the production method of
an existing product is changed. Finally, the benefits of
this more intelligent updating procedure are obvious
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
58

in comparison with a dummy periodic update proce-
dure (when the model is updated at one-year intervals,
for example, the prediction error means of the whole
data sets are 12.24 using criterion 1 and 16.34 using
criterion 2, notably worse than the results achieved
with our method, 12.07 and 15.67). The periodic pro-
cedure could not react to changes quickly or accu-
rately enough, and in some cases it would react un-
necessarily.
6 CONCLUSIONS
This paper described the development of a method for
detecting the need for a model update in the steel in-
dustry. The prediction accuracy of regression mod-
els may decrease in the long run, and a model update
at periodic intervals may not react to changes rapidly
and accurately enough. Thus, there was a need for a
reliable method for determining suitable times to up-
date the model. Two limits were used to detect these
update times, and the results appear promising. In
addition, it is possible to rework the actual values of
the limits to optimize the updating steps and improve
the results before implementing the method in an ac-
tual application environment. Although the procedure
was tested using a single data set, the extensiveness of
the data set clearly proves the usability of the proce-
dure. Nevertheless, the procedure will be validated
when it is adapted also to regression models devel-
oped to model the tensile strength and elongation of
metal plates.
In this study the model update was performed by
using all the previously gathered data to define the re-
gression model parameters. However, in the future the
amount of data will increase, making it hard to use all
the gathered data in an update. Thus, new methods for
intelligent data selection are needed to form suitable
training data. In addition, the model update could be
developed into a direction where the input variables
of the regression model can also be changed during
the update.
REFERENCES
Gabrys, B., Leivisk
¨
a, K., and Strackeljan, J. (2005). Do
Smart Adaptive Systems Exist, A Best-Practice for
Selection and Combination of Intelligent Methods.
Springer-Verlag, Berlin, Heidelberg.
Haykin, S. (1999). Neural Networks, A Comprehensive
Foundation. Prentice Hall, Upper Saddle River, New
Jersey.
Juutilainen, I. and R
¨
oning, J. (2006). Planning of strength
margins using joint modelling of mean and dispersion.
Materials and Manufacturing Processes, 21:367–373.
Juutilainen, I. and R
¨
oning, J. (2007, in press). A method for
measuring distance from a training data set. Commu-
nications in Statistics.
Juutilainen, I., R
¨
oning, J., and Myllykoski, L. (2003). Mod-
elling the strength of steel plates using regression
analysis and neural networks. Proceedings of Interna-
tional Conference on Computational Intelligence for
Modelling, Control and Automation, pages 681–691.
Khattree, R. and Rao, C., editors (2003). Statistics in indus-
try - Handbook of statistcs 22. Elsevier.
Yang, M., Zhang, H., Fu, J., and Yan, F. (2004). A
framework for adaptive anomaly detection based on
support vector data description. Lecture Notes in
Computer Science, Network and Parallel Computing,
pages 443–450.
DETECTION OF THE NEED FOR A MODEL UPDATE IN STEEL MANUFACTURING
59
