
HIGHER ORDER SLIDING MODE STABILIZATION OF A
CAR-LIKE MOBILE ROBOT
F. Hamerlain, K. Achour
Laboratoire de Robotique et d’intelligence Artificielle, CDTA, Cit
´
e du 20 Ao
ˆ
ut 1956, BP 17, Baba Hassen, Alger, Algeria
T. Floquet, W. Perruquetti
LAGIS, UMR CNRS 8146, Ecole Centrale de Lille, BP 48, Cit
´
e Scientifique, 59651 Villeneuve-d’Ascq Cedex, France
Keywords:
Nonholonomic systems, Higher order sliding modes, Finite time stabilization, Car-like mobile robot.
Abstract:
This paper deals with the robust stabilization of a car-like mobile robot given in a perturbed chained form. A
higher order sliding mode control strategy is developed. This control strategy switches between two different
sliding mode controls: a second order one (super-twisting algorithm) and a new third order sliding mode con-
trol that performs a finite time stabilization. The proposed third sliding mode controller is based on geometric
homogeneity property with a discontinuous term. Simulation results show the control performance.
1 INTRODUCTION
In the recent years, the control of nonholonomic sys-
tems has received a considerable attention, and in par-
ticular the stabilization problem. Due to the peculiar
nature of nonholonomic kinematics, the stabilization
problem addressed in control design for wheeled mo-
bile robots (WMR) is in general quite difficult. In
fact, it is known that nonholonomic WMR with re-
stricted mobility (such as unicycle-type and car-like
vehicles) cannot be stabilized to a desired configura-
tion (or posture) via differentiable, or even continu-
ous, pure-state feedback control despite they are open
loop controllable (Brockett, 1983). Several nonlin-
ear control designs have been proposed to achieve the
stabilization for such systems. Time-varying feed-
backs (Samson, 1995) or (open loop) sinusoidal and
polynomial controls (Murray and Sastry, 1993) can
be developed. Other alternatives consist in using the
backstepping recursive techniques (Jiang and Nijmei-
jer, 1999), (Huo and Ge, 2001), flatness (M. Fliess
et al., 1995), or discontinuous approaches (Astolfi,
1996), (Floquet et al., 2003). The robustness property
is an important aspect for stabilizing tasks of uncer-
tain systems, especially when there exist disturbances
or errors dynamics in the system. It is well known
that the standard sliding mode features are high ac-
curacy and robustness with respect to various internal
and external disturbances. The basic idea is to force
the state via a discontinuous feedback to move on a
prescribed manifold called the sliding manifold. A
specific drawback involved by sliding mode technique
is the well known chattering effect (undesirable vibra-
tions), which limits the practical relevance. To over-
come this drawback, the Higher Order Sliding Mode
(HOSM) approach has been proposed (Emel’yanov et
al., 1993). The main objective is to keep the slid-
ing variable and a finite number of its successive time
derivatives to zero through a discontinuous function
acting on some high order time derivative of the slid-
ing variable. This technique generalizes the basic
sliding mode idea and can be implemented for sys-
tems with arbitrary relative degree. Keeping the main
advantages of the standard sliding mode control, the
chattering effect is avoided and finite time conver-
gence together with higher order precision are pro-
vided. Actually, the problem of higher order sliding
mode control is equivalent to the finite time stabi-
lization of an integrator chain with nonlinear uncer-
tainties. In (Floquet et al., 2003), it is shown that
the HOSM theory is efficient to design control laws
which robustly stabilizes in finite time a chained form
system. Second order sliding mode controllers were
proposed to stabilize a three-dimensional system (uni-
cycle type vehicle). It should be pointed out that, in
the case of the four dimensional car-like robot sys-
tem, the proposed procedure requires the finite time
stabilization of a third order integrator chain. Thus, a
195
Hamerlain F., Achour K., Floquet T. and Perruquetti W. (2007).
HIGHER ORDER SLIDING MODE STABILIZATION OF A CAR-LIKE MOBILE ROBOT.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 195-200
DOI: 10.5220/0001639901950200
Copyright
c
SciTePress

third order sliding mode control is at least necessary
and a new type of third order sliding mode algorithm
is introduced in this paper.
The aim of this paper is to present a high or-
der sliding mode control strategy for the robust sta-
bilization problem of a car-like mobile robot. First,
the perturbed one-chain form of the robot is derived.
Then, second order sliding mode controllers based on
the so-called super twisting algorithm and a third or-
der sliding mode controller are developed. The latter
controller is a combination of a finite time controller
based on geometric homogeneity and a discontinuous
term that ensures robustness properties. By switching
between these sliding mode controllers, a finite time
stabilization to the origin is obtained.
The organization of this paper is as follows: Sec-
tion 2 presents the perturbed chained form model of
the car-like vehicle and states the problem under inter-
est. Section 3 deals with the design of the hybrid con-
trol law strategy via higher order sliding mode tech-
nique. Simulation results are presented in Section 4.
2 CAR-LIKE ROBOT MODEL
AND PROBLEM STATEMENT
As mentioned in (Murray and Sastry, 1993), many
nonlinear mechanical systems that belong to the class
of driftless nonholonomic systems (the knife-edge, ar-
ticulated vehicles, a car towing several trailers, etc...)
can be transformed via change of coordinates in the
state and control spaces into a so-called chained form.
In this paper, we are particularly concerned with non-
holonomic systems whose trajectories can be written
as the solution of the driftless system:
˙x = g
1
(x)u
1
+ g
2
(x)u
2
(1)
where x ∈ℜ
n
is the state vector, u
1
, u
2
∈ℜ are the two
control inputs, g
1
, g
2
are smooth linearly independent
vector fields. We are interested in the case of n = 4
which is the example of a car-like mobile robot. The
kinematic model of the robot in a single drive mode is
given by:
˙x = cos(θ) u
1
˙y = sin(θ) u
1
˙
θ =
tan(φ)
L
u
1
˙
φ = u
2
(2)
where (x,y) are the Cartesian coordinates of the cen-
ter of the rear axle, θ is the orientation angle of the
vehicle with respect to a fixed frame, φ is the steering
angle relative of the car body and u
1
, u
2
are respec-
tively the driven and the steering velocities.
For θ ∈
−
π
2
,
π
2
, let us consider the following
transformation on the control input vector:
w =
cos(θ) 0
0 1
u
and let us introduce perturbations in the model. Then,
the behavior of the robot can be described by the fol-
lowing system:
˙q = g
1
w
1
+ g
2
w
2
+ γ(x,t) (3)
with q = (x, y,θ, φ)
T
, g
1
(q) =
1,tan(θ),
tan(φ)
Lcos(θ)
,0
T
,
g
2
(q) = (0, 0,0, 1)
T
. γ(x,t) ∈ ℜ
n
is an additive per-
turbation assumed to be smooth enough. In (Murray
et al., 1994), conditions are given for a nonholonomic
systems (1) to be transformed into a so-called one-
chained form.
By using the diffeomorphism and the control input
space transformation given in (Murray et al., 1994)
z
1
= x
z
2
=
tan(φ)
Lcos(θ)
3
z
3
= tan(θ)
z
4
= y
(4)
(
v
1
= w
1
= u
1
cos(θ)
v
2
=
3tan(φ)
2
sin(θ)
L
2
cos(θ)
3
w
1
+
1
Lcos(θ)
3
cos(φ)
2
w
2
, (5)
for φ ∈
−
π
2
,
π
2
, the system (3) is transformed in the
following perturbed one-chained form
˙z
1
= v
1
+ γ
1
(z,t)
˙z
2
= v
2
+ γ
2
(z,t)
˙z
3
= z
2
(v
1
+ γ
1
(z,t))
˙z
4
= z
3
(v
1
+ γ
1
(z,t))
(6)
if and only if γ(x,t) belongs to the distribution
spanned by g
1
(x) and g
2
(x) (Floquet et al., 2000).
In the following, γ
1
and γ
2
are supposed to be
bounded for all z ε Ω (an open set in ℜ
4
) and for all t
as follows:
γ
1
(z,t)
≤ σ
1
γ
2
(z,t)
≤ σ
2
˙
γ
1
(z,t)
≤ σ
′
1
where σ
1
, σ
2
, σ
′
1
are positive constants.
Problem: Find a robust control law for the car-like
robot model (6) guaranteeing the finite time stabiliza-
tion at the origin (x = 0, y = 0, θ = 0, φ = 0) in the
presence of matched disturbances.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
196

3 FINITE TIME STABILIZATION
VIA HIGHER ORDER SLIDING
MODES
3.1 Higher Order Sliding Modes
In this approach, the designed control law will switch
between second order and third order sliding mode al-
gorithms in order to obtain the finite time stabilization
of (6). It is assumed that the reader is familiar with the
sliding mode theory (see (Emel’yanov et al., 1993),
(Fridman and Levant, 2002) or (Perruquetti and Bar-
bot, 2002) for further details). Let us just briefly recall
that the principle of higher order sliding mode control
is to constrain, by the mean of a discontinuous control
acting on the r
th
time derivative of a suitably chosen
sliding variable S : ℜ
+
×ℜ
n
→ℜ, the system trajec-
tories to reach and stay, after a finite time, on a given
sliding manifold S
r
in the state space defined by:
S
r
=
n
S(t, x) =
˙
S(t, x) = ... = S
(r−1)
(t, x) = 0
o
,
where x ∈ℜ
n
is the state system. A control law lead-
ing to such a behavior will be called a r
th
order ideal
sliding mode algorithm with respect to S.
Arbitrary-order sliding mode controllers with fi-
nite time convergence have been proposed in (Levant,
2001) and (Levant, 2003). As the control algorithm
proposed in (Levant, 2001) requires the knowledge of
high order time derivatives of the output, the author in
(Levant, 2003) proposes the use of a robust exact fi-
nite time convergence differentiators based on the su-
per twisting algorithm. The implementation of these
controllers is not easy since some singularities in the
time derivatives of the sliding variable may appear. In
(Laghrouche et al., 2004), a third order sliding mode
controller that combines a standard sliding mode con-
trol with a linear quadratic one has been proposed.
However, it directly depends on the initial conditions
of the system and complex off-line computations are
needed before starting the control action. A higher or-
der sliding mode control strategy with smooth mani-
fold leading to a practical convergence was developed
in (Djemai and Barbot, 2002). Based on this strat-
egy, a real third order sliding mode controller with
time varying smooth manifolds was designed for the
practical stabilization of a unicycle-type mobile robot
(Barbot et al., 2003).
3.2 Finite Time Stabilization of the
Car-like Robot
The stabilization of (6) is made in three steps by
switching between different types of sliding mode
controllers:
First step:
The control algorithm is first to constrain the sub-
system:
˙z
1
= v
1
+ γ
1
(z,t) (7)
to evolve after a finite time on the sliding manifold
s
1
= z
1
−at = 0, a > 0.
The subsystem (7) has relative degree one with re-
spect to s
1
and the second time derivative of s
1
is
given by:
..
s
1
= ˙v
1
+
˙
γ
1
(z,t).
The chosen sliding mode algorithm is the super twist-
ing algorithm which has been developed for systems
with relative degree one to avoid chattering. The con-
trol law v
1
is given as follows:
v
1
= −λ
1
|
s
1
|
1
2
sign(s
1
) +v
11
,
˙v
11
= −α
1
sign(s
1
),
(8)
where α
1
, λ
1
are positive constants that satisfy the
following conditions (Levant, 2003):
α
1
> σ
′
1
λ
2
1
> 4σ
′
1
α
1
+ σ
′
1
α
1
−σ
′
1
This ensures that the trajectories reach the sliding
manifold Γ
1
=
{
z ∈ Ω : s
1
= ˙s
1
= 0
}
in a finite time
T
1
and stay it after T
1
. Thus, for t ≥ T
1
, the resulting
dynamics, in sliding motion, is given by:
˙z
1
= a,
˙z
2
= v
2
+ γ
2
(z,t),
˙z
3
= az
2
,
˙z
4
= az
3
.
(9)
Second step:
When the state trajectory evolves in Γ
1
, the dy-
namics of the subsystem
˙z
2
= v
2
+ γ
2
(z,t),
˙z
3
= az
2
,
˙z
4
= az
3
.
(10)
is equivalent to a perturbed triple chain of integrator.
The finite time stabilization of (10) can be obtained
using a 3
rd
order sliding mode algorithm for v
2
. A
new kind of algorithm is presented here. The control
law v
2
is made of two terms:
v
2
= v
2,id
+ v
2,vss
where v
2,id
is an ideal control, based on the geomet-
ric homogeneity approach, and that ensures the finite
time stabilization of the system (9) without perturba-
tions. v
2,vss
is a discontinuous part of the control v
2
allowing to reject the uncertainties.
HIGHER ORDER SLIDING MODE STABILIZATION OF A CAR-LIKE MOBILE ROBOT
197

a. Control design of v
2,id
Consider the system (10) without perturbations:
˙z
2
= v
2,id
˙z
3
= az
2
˙z
4
= az
3
(11)
and let us define a control law v
2,id
stabilizing
¯z =(z
2
, z
3
, z
4
)
T
to zero in finite time.
To this end, let k
1
,k
2
,k
3
> 0 be such that the poly-
nomial p
3
+ k
3
p
2
+ k
2
p + k
1
is Hurwitz. From
the works (Bhat and Bernstein, 2005), there exists
ε ∈ (0,1) such that, for every, β ∈ (1 −ε, 1), the
origin is a globally finite time stable equilibrium
for (11) via the state feedback:
v
2,id
= −k
1
sign(z
4
)
|
z
4
|
β
1
−k
2
sign(z
3
)
|
z
3
|
β
2
−k
3
sign(z
2
)
|
z
2
|
β
3
(12)
with
(
β
i−1
=
β
i
β
i+1
2β
i+1
−β
i
, i = 2, 3
β
3
= β, β
4
= 1
This ensures that the following equalities hold af-
ter a finite time T
2,i
:
z
2
= z
3
= z
4
= 0.
b. Control design of v
2,vss
For perturbation rejection, the following sliding
variable s ∈ ℜ is introduced:
s = s
0
(z
2
,z
3
,z
4
) +s
2
(13)
Here, s
0
is a quite conventional sliding mode vari-
able, selected such that
∂s
0
∂¯z
[1,0,0]
T
6= 0 (relative
degree one requirement). One can choose
s
0
= z
2
.
s
2
is an additional term that enables integral con-
trol to be included such that
˙s
2
= −v
2,id
.
Let us show that a sliding motion can be induced
on s = 0 by using the discontinuous control
v
2,vss
= −Dsign(s) (14)
where the switching gain satisfies:
D > σ
2
.
For this, define a Lyapunov functionV as follows:
V =
1
2
s
2
The time derivative of this function is given by:
˙
V = s(v
2
+ γ
2
+ ˙s
2
)
= s(v
2,id
+ v
2,vss
+ γ
2
(z,t) −v
2,id
)
= s(γ
2
(z,t) −Dsign(s))
≤ σ
2
|
s
|
−D
|
s
|
≤ −G
√
V, G > 0
Hence, the trajectories of the system converge in
a finite time T
2,v
on the sliding manifold given
by
{
s = 0
}
. When sliding, the equivalent con-
trol denoted by v
2,eq
(see (Edwards and Spurgeon,
1998), p. 34 for a definition), required to maintain
the sliding motion on the surface s = 0, is obtained
by writing that ˙s = 0:
˙s = ˙s
0
+ ˙s
2
= v
2,eq
+ v
2,id
+ γ
2
(z,t) −v
2,id
(15)
= 0
Thus:
v
2,eq
= −γ
2
(z,t)
and the equivalent dynamics on s = 0 is given by
the system (11). This implies that the trajectory
enters the set
Γ
2
=
{
z ∈ Ω : z
2
= z
3
= z
4
= 0
}
after a finite time T
2
= T
2,i
+ T
2,v
.
Third step:
When z ∈ Γ
1
∩Γ
2
, the controls are switched to:
v
1
= −λ
11
|
z
1
|
1
2
sign(z
1
) +w
11
˙w
11
= −α
11
sign(z
1
)
(16)
v
2
= −λ
22
|
z
2
|
1
2
sign(z
2
) +w
22
˙w
22
= −α
22
sign(z
2
)
(17)
With a suitable choice of the positive constants α
11
,
λ
11
, α
22
and λ
22
(see (Levant, 2003)), a sliding mo-
tion is obtained on the manifolds
{
z
1
= ˙z
1
= 0
}
and
{
z
2
= ˙z
2
= 0
}
after a finite time T
3
. This allows to
maintain z
2
equals to zero (and so z
3
= z
4
= 0), and
to reach the manifold z
1
= 0, so that the global system
is stabilized in a finite time lower than T
1
+ T
2
+ T
3
.
4 SIMULATION RESULTS
In this section, simulation results for the finite time
stabilization of the car-like robot are presented. The
sampling time is set to be τ = 0.01s with the physi-
cal parameter L = 1.2m. The design parameters of the
second order sliding mode controllers are:
a = 3, λ
1
= 5, λ
11
= λ
2
= 1, α
1
= α
11
= α
22
= 0.5
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
198
while for the third order one, they are:
k
1
= 1, k
2
= k
3
= 1.5, D = 0.97,
β
1
= 2/3, β
2
= 3/5, β
3
= 3/4.
The perturbations are taken as band limited white
noises with unit variance. The results of the stabi-
lization are given in Figures 1, 2, 3 with the initial
conditions:
z
1
= x = 0.5m,z
2
= z
3
= 0, z
4
= y = 1.4m.
Figures 1, 2 and 3 show that the control problem is
fulfilled since the state trajectory of the robot con-
verges to zero in a robust manner. One can note
(Figure 1) that z
4
tends to zero (≈ 5s) faster than z
3
(≈5.2s), and z
2
(≈5.4s). Once z
2
= 0, the control v
1
switches in the third step and z
1
reaches the origin in
finite time (13s). Figure 2 gives the angles behaviour
and the trajectory of the robot in the phase plan (x,y),
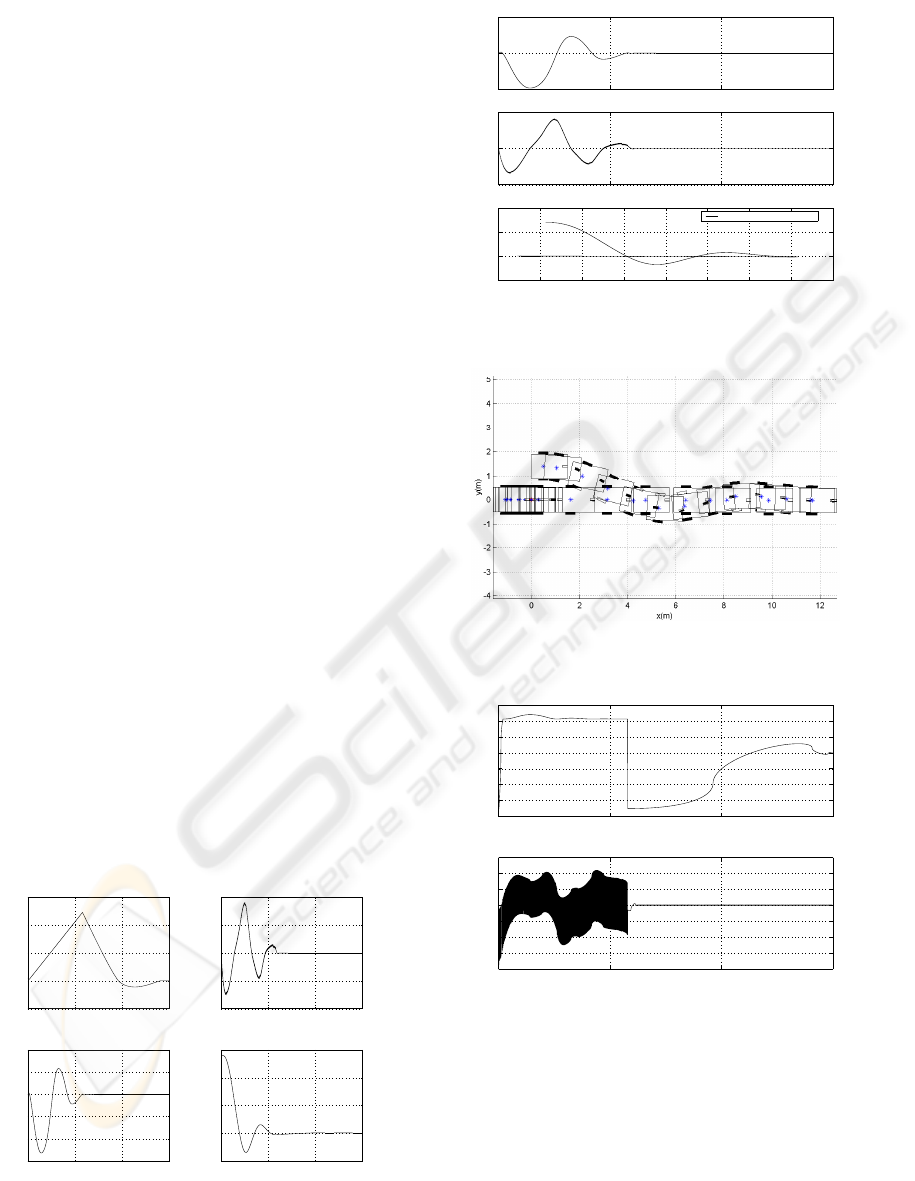
while Figure 3 shows the movement of the robot. The
choice of a second order sliding mode controller (su-
per twisting algorithm) in the first and third steps al-
lows to overcome the chattering phenomenon since
the discontinuity is acting on the first time derivative
of the control v
1
. Indeed, the trajectory of the system
is smoother as there are few uncertainties on the in-
formation injected in the equivalent dynamics in the
second step. Also, it can be seen on the behavior of
the actual control inputs (Figure 4), that the driven
velocity is not affected by the chattering effect. How-
ever, the steering velocity still exhibits some chatter-
ing in the second step due to the discontinuous part of
the control v
2
. In practice, the chattering phenomenon
can be reduced by using sigmo
¨
ıd functions instead of
the signum function. Another solution would be the
use of a second order sliding mode algorithm in (14).
0 5 10 15
−5
0
5
10
15
t(s)
z1(m)
0 5 10 15
−0.4
−0.2
0
0.2
0.4
t(s)
z2
0 5 10 15
−0.6
−0.4
−0.2
0
0.2
0.4
t(s)
z3
0 5 10 15
−0.5
0
0.5
1
1.5
t(s)
z4(m)
Figure 1: Coordinates z
1
, z
2
, z
3
, z
4
.
0 5 10 15
−0.5
0
0.5
t(s)
teta(rd)
0 5 10 15
−0.5
0
0.5
t(s)
phi(rd)
−2 0 2 4 6 8 10 12 14
−1
0
1
2
x(m)
y(m)
Phase trajectory of Robucar
Orientation
Steering
Figure 2: Angles and phase trajectory.
Figure 3: Movement of the Robot.
0 5 10 15
−4
−3
−2
−1
0
1
2
3
t(s)
u1(m/s)
0 5 10 15
−2
−1.5
−1
−0.5
0
0.5
1
1.5
t(s)
u2(rd/s)
Driven velocity
Steering velocity
Figure 4: Actual control inputs.
5 CONCLUSION
This paper has presented a higher order sliding mode
control solution for the robust stabilization problem
applied to a car-like robot. Based on the perturbed
chain form of the robot, control laws, switching be-
tween different higher order sliding mode controllers,
have been developed to obtain a robust finite time sta-
HIGHER ORDER SLIDING MODE STABILIZATION OF A CAR-LIKE MOBILE ROBOT
199

bilization. One contribution of this paper is the design
of a 3
rd
order sliding mode control based on geomet-
ric homogeneity property with a discontinuous term.
Future work concerns the experimental test of the pro-
posed control approach.
REFERENCES
Astolfi A. (1996). Discontinuous control of nonholonomic
systems, Systems & Control Letters Vol. 27, pp. 37–
45.
Barbot J.-P., Djemai M., Floquet T. and Perruquetti W.
(2003). Stabilization of a unicycle-type mobile robot
using higher order sliding mode control. In Proc. of
the 41st IEEE Conference on Decision and Control.
Bhat, S. and Bernstein, D. (2005). Geometric Homogeneity
with applications to finite time stability. Mathematics
of Control, Signals and Systems, Vol. 17, pp. 101–127.
Brockett, R. (1983). Asymptotic stability and feedback sta-
bilization. In Differential geometric control theory,
pp. 181–191, Birkhauser.
Djemai M. and Barbot J.-P. (2002). Smooth manifolds and
high order sliding mode control. In Proc. of the 41st
IEEE Conference on Decision and Control.
Edwards C. and Spurgeon S. (1998). Sliding mode control:
theory and applications. Taylor and Francis Eds.
Emel’yanov S.V., Korovin S.V., and Levantovsky L.V.
(1993). Higher order sliding modes in control sys-
tems. Differential Equations, Vol. 29, pp. 1627–1647.
Floquet T., Barbot J.-P. and Perruquetti W. (2000). One-
chained form and sliding mode stabilization for a non-
holonomic perturbed system. American Control Con-
ference, Chicago, USA.
Floquet T., Barbot J.-P. and Perruquetti W. (2003). Higher
order sliding mode stabilization for a class of non
holonomic perturbed system. Automatica, Vol. 39, pp.
1077–1083.
Fliess M., Levine J., Martin P. and Rouchon P. (1995). Flat-
ness and defect of non-linear systems: Introductory
theory and examples. International Journal on Con-
trol, Vol.61, pp. 1327–1361.
Fridman L. and Levant A. (2002). Higher order sliding
modes. In Sliding Mode Control in Engineering, W.
Perruquetti and J. P. Barbot (Eds), Marcel Dekker, pp.
53–101.
Huo W. and Ge S. (2001). Exponential stabilization of non-
hononomic systems: an ENI approach. International
Journal of Control, Vol. 74, 1492–1500.
Jiang, Z. and Nijmeijer, H. (1999). A recursive tech-
nique for tracking control of nonholonomic systems
in chained form. IEEE Tansactions on Automatic Con-
trol, Vol. 44, pp. 265–279.
Laghrouche S., Smaoui M. and Plestan F. (2004). Third-
order sliding mode controller for electropneumatic ac-
tuators. In Proc. of the 43rd IEEE Conference on De-
cision and Control.
Levant, A. (2001). Universal SISO sliding-mode controllers
with finite-time convergence. IEEE Transactions on
Automatic Control, Vol. 46, pp. 1447–1451.
Levant, A. (2003). Higher-order sliding modes, differentia-
tion and output-feedback control. International Jour-
nal of Control, Vol. 76, pp. 924–941.
Murray R. and Sastry S. (1993). Nonholonomic motion
planning :steering using sinusoids. IEEE. Tansactions
On Automatic Control, Vol. 38, pp. 77–716.
Murray R., Li Z. and Sastry S. (1994). A Mathematical In-
troduction to Robotic Manipulation. CRC Press, Inc.,
Florida, USA.
Perruquetti W. and Barbot J.-P. (Editors) (2002), Sliding
Mode Control in Engineering, Marcel Dekker.
Samson C. (1995). Control of chained systems. Applica-
tion to path following and time-varying point stabi-
lization of mobile robots. IEEE Tansactions on Auto-
matic Control, Vol. 40, pp. 64–77.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
200
