DISCRETE GENETIC ALGORITHM AND REAL ANT COLONY
OPTIMIZATION FOR THE UNIT COMMITMENT PROBLEM
Guillaume Sandou
Supélec, Automatic Control Department – 3, rue Joliot Curie – 91192 Gif-sur-Yvette France
Keywords: Metaheuristics, unit commitment, ant colony, genetic algorithm, scheduling.
Abstract: In this paper, a cooperative metaheuristic for the solution of the Unit Commitment problem is presented.
This problem is known to be a large scale, mixed integer problem. Due to combinatorial complexity, the
exact solution is often intractable. Thus, a metaheuristic based method has to be used to compute a near
optimal solution with low computation times. A new approach is presented here. The main idea is to couple
a genetic algorithm to compute binary variables (on/off status of units), and an ant colony based algorithm
to compute real variables (produced powers). Finally, results show that the cooperative method leads to the
tractable computation of a satisfying solution for medium scale Unit Commitment problems.
1 INTRODUCTION
The Unit Commitment problem is a mixed integer
problem, referring to the optimal scheduling of
several production units, satisfying consumer’s
demand and technical constraints. Integer variables
are the on/off status of production units, and real
variables are produced powers. Numerous methods
have been applied; see (Sen and Kothari, 1998).
The first idea is to use an exact solution method:
exhaustive enumeration, “Branch and Bound” (Chen
and Wang, 1993), dynamic programming (Ouyang
and Shahidehpour, 1991). Due to temporal coupling
of constraints (time up / time down constraints), a
large temporal horizon is required, leading to a large
number of binary variables: exact methods suffer
from combinatorial complexity. Approximated
methods are required for tractable results.
Deterministic approximated methods have been
tested: priority lists in (Senjyu, et al., 2004) or expert
systems. Due to numerous constraints, this kind of
methods are often strongly suboptimal. Constraints
are considered by the Lagrangian relaxation method,
see (Zhai and Guan, 2002). Multi unit coupling
constraints are relaxed. As a result, the unit
Commitment problem is divided into several smaller
optimization problems. However, due to the non
convexity of the objective function, no guarantee
can be given on the duality gap and the actual
optimality of the solution. Further, an iterative
procedure has to be used: solution of the
optimization problems with fixed Lagrange
multipliers, updates of these multipliers, and so on.
This update can be performed with genetic
algorithms as in (Cheng, et al., 2000) or by
subgradient methods (Dotzauer, et al., 1999).
Stochastic approximated algorithms, called
metaheuristics are potentially interesting methods
for Unit Commitment as they are able to compute
near optimal solutions with low computation times.
A simulated annealing approach is used in (Yin Wa
Wong, 1998), tabu search is used in (Rajan and
Mohan, 2004) and genetic algorithms are used in
(Kasarlis, et al., 1996). Cooperative algorithms have
been developed to couple the advantages of several
optimization methods: genetic algorithms and
simulated annealing are used in (Cheng, et al.,
2002); simulated annealing and local search in
(Purushothama and Jenkins, 2003).
In (Serban and Sandou, 2007), a mixed ant
colony method has been proposed. The approach is
interesting, but, due to the positive feedback of ant
colony, may quickly converge to local minima. To
circumvent this problem, a new cooperative strategy
is defined in this paper. The idea is to use a
knowledge based genetic algorithm for binary
variables to achieve a deep exploration of the search
space, and simultaneously an ant colony based
algorithm for real variables.
The paper is organized as follows. In section 2,
the Unit Commitment problem is briefly called up.
256
Sandou G. (2007).
DISCRETE GENETIC ALGORITHM AND REAL ANT COLONY OPTIMIZATION FOR THE UNIT COMMITMENT PROBLEM.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 256-261
DOI: 10.5220/0001641602560261
Copyright
c
 SciTePress

The cooperative metaheuristic ant colony/genetic
algorithm method is depicted in section 3. Both
algorithms are described, together with the definition
of a criterion guaranteeing feasibility of the solution.
Numerical results are given in section 4. Finally,
concluding remarks are drawn in section 5.
2 UNIT COMMITMENT
PROBLEM
The Unit Commitment problem is a classical large
scale mixed integer optimization problem.
Following notations are used throughout the paper:
 N: length of time horizon,
 n: (subscript) : time interval number n,
 K: number of production unit,
 k (superscript): production unit number k,

k
n
u : on/off status of production unit k during
time interval n (binary variable),

k
n
Q : power produced by production unit k
during time interval n (real variable).
2.1 Cost Function
The objective function is the sum of production,
start-up, and shut-down costs for all time intervals
and all units:
{}
∑∑
==
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
N
n
K
k
k
n
k
n
k
off/on
k
n
k
n
k
prod
Q,u
u,uc
u,Qc
k
n
k
n
11
1
)(
)(
min
,
(1)
where production cost of unit k can be expressed by:
,)(),(
01
2
2
k
n
kk
n
kk
n
kk
n
k
n
k
prod
uQQuQc ααα ++=
(2)
start-up cost and shut-down costs are:
,)1()1(
)(
11
1
k
n
k
n
k
off
k
n
k
n
k
on
k
n
k
n
k
off/on
uucuuc
u,uc
−+−
=
−−
−
(3)
and
k
off
k
on
kkk
cc and,,,
012
ααα are technical data of
production unit k.
2.2 Constraints
Constraints are:
 Capacity constraints
k
n
kk
n
k
n
k
uQQuQ
maxmin
≤≤
(4)
 Consumers’ demand satisfaction
dem
n
K
k
k
n
QQ ≥
∑
=1
(5)
 Time up and time down constraints
⎟
⎠
⎞
⎜
⎝
⎛
===⇒
==
⎟
⎠
⎞
⎜
⎝
⎛
===⇒
==
−+
++
−
−+
++
−
0,,0,0
)0,1(
1,,1,1
)1,0(
1
21
1
1
21
1
k
Tn
k
n
k
n
k
n
k
n
k
Tn
k
n
k
n
k
n
k
n
k
down
k
up
uuu
uu
uuu
uu


(6)
Such constraints are temporally coupling
constraints which express dynamics on production
units.
k
down
k
up
kk
TT,Q,Q and
maxmin
are technical data.
3 COOPERATIVE
METAHEURISTIC SOLUTION
3.1 Algorithm Principles
As already mentionned, Unit Commitment is a large
scale mixed integer programming problem. Genetic
algorithm is a well known algorithm for
combinatorial optimization problems. In this study, a
specific criterion is defined (see section 3.2), based
on particular penalty functions to guarantee the
solution feasibility. Genetic algorithm is used to
compute binary variables and is depicted in section
3.3. Further, a stochastic algorithm is simultaneously
used to compute real variables, based on ant colony
optimization. It is presented in section 3.4.
3.2 Optimization Criterion
3.2.1 Criterion Expression
Consider that a feasible solution is known with a
cost c
f
. The following optimization criterion is
defined:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
++
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
∑∑
==
−
=
=
=
)()).()1((
),(
),(
min
11
1/
,,1
,,1
),(
yByhc
uuc
uQc
f
N
n
K
k
k
n
k
n
k
offon
k
n
k
n
k
prod
Kk
Nn
Quy
k
n
k
n
ε
…

,
(7)
where:

ε
is a small positive real,

)( yh is a penalty function for non feasible
solutions,
DISCRETE GENETIC ALGORITHM AND REAL ANT COLONY OPTIMIZATION FOR THE UNIT COMMITMENT
PROBLEM
257


)( yB
is a boolean function (1 for non feasible
solutions and 0 for feasible ones).
With this criterion, any unfeasible solution has a
higher cost than the feasible known solution: any
unconstrained optimization algorithm can solve the
problem. Thus, an elitist genetic algorithm can be
used. The definition of criterion (7) only supposed
that a feasible solution is known. It can be easily
computed using a simple priority list. This is a very
suboptimal solution, but the quality of this first
feasible solution is not crucial, as the criterion can
be updated when new feasible solutions are known.
3.2.2 Penalty Expression
The following variables are added:
)1(
)1(
1
1
k
n
k
n
k
n
k
n
k
n
k
n
uu
uu
−=
−=
−
−
ε
δ
(8)
With these variables, time-up and time-down
constraints are expressed by linear expressions:
k
n
k
up
T
j
k
jn
k
Tn
k
n
k
n
Tu
uu
up
k
k
up
δ
δ
≥⇔
==⇒=
∑
−
=
+
−+
+
1
0
1
1
)1,,1(1 …
(9)
k
n
k
down
T
j
k
jn
k
Tn
k
n
k
n
Tu
uu
down
k
k
down
ε
ε
≥−⇔
==⇒=
∑
−
=
+
−+
+
1
0
1
1
)1(
)0,,0(1
…
(10)
Capacity constraints and consumers’ demands
satisfaction are linear. All constraints can be
expressed by a linear equation,
cc
BxA ≤ , where x is
Tk
n
k
n
k
n
k
n
K,,k;N,,n;,,Q,u )11( …… == εδ , leading
to a high tractability of the boolean and the penalty
functions computation.
3.3 Genetic Algorithm for on/off
Variables
3.3.1 Algorithm Principles
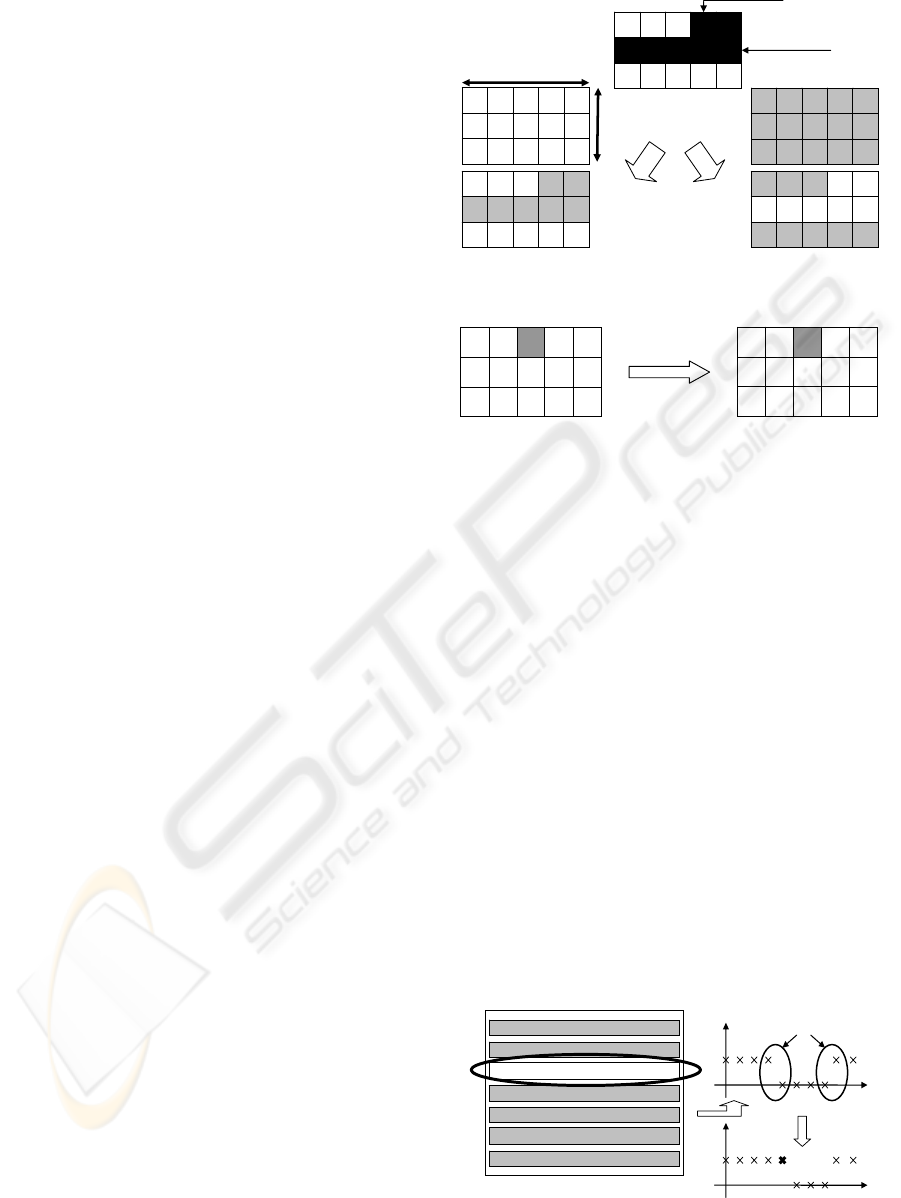
Genetic algorithm is a well known optimization
method. Fig. 1 and 2 represent classical cross-over
and mutation operators for Unit Commitment
problem.
0
0
111
110
0
1
01000
N périods
1
0
0 0 1
1 1 0
0
0
0 1 0 1 1
0
0
111
110
0
0
01000
1
0
0 0 1
1 1 0
0
1
0 1 0 1 1
Children
Parents
2 random points
K
units
mask
Figure 1: Classical crossing over operator.
0
0
111
110
0
1
01000
0
0
1 0 1
1 1 0
0
1
0 1 0 0 0
Parent Child
Figure 2: Classical mutation operator.
Individuals are in a matrix form. Crossover
operator create 2 potentially low cost children from
2 parents by merging their variables (or genes). The
mutation operator allows the introduction of new
genes in the population by randomly changing one
of the variables. Finally, the selection operator is
performed with a classical biased roulette method.
3.3.2 Knowledge Based Operators
It has been observed that the genetic algorithm can
be more efficient by using some knowledge based
operators. New genetic operators are added,
considering properties of the problem. The first
operator is a “selective mutation operator”. Consider
unit scheduling of fig. 3. Due to time-up and time-
down constraints, a classical mutation leads very
often to an infeasible solution. To increase the
probability of reaching a new feasible point, a
“selective mutation operator” is introduced: this
operator detects switching times and allows a
random mutation only for these genes.
1 1 1 1 1 1 0 0 0 0
Switching times :
Authorized
m
utat
i
o
n
s
Figure 3: Selective mutation operator.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
258

0 1 1 1 0
1 0 0 1 1
N
K
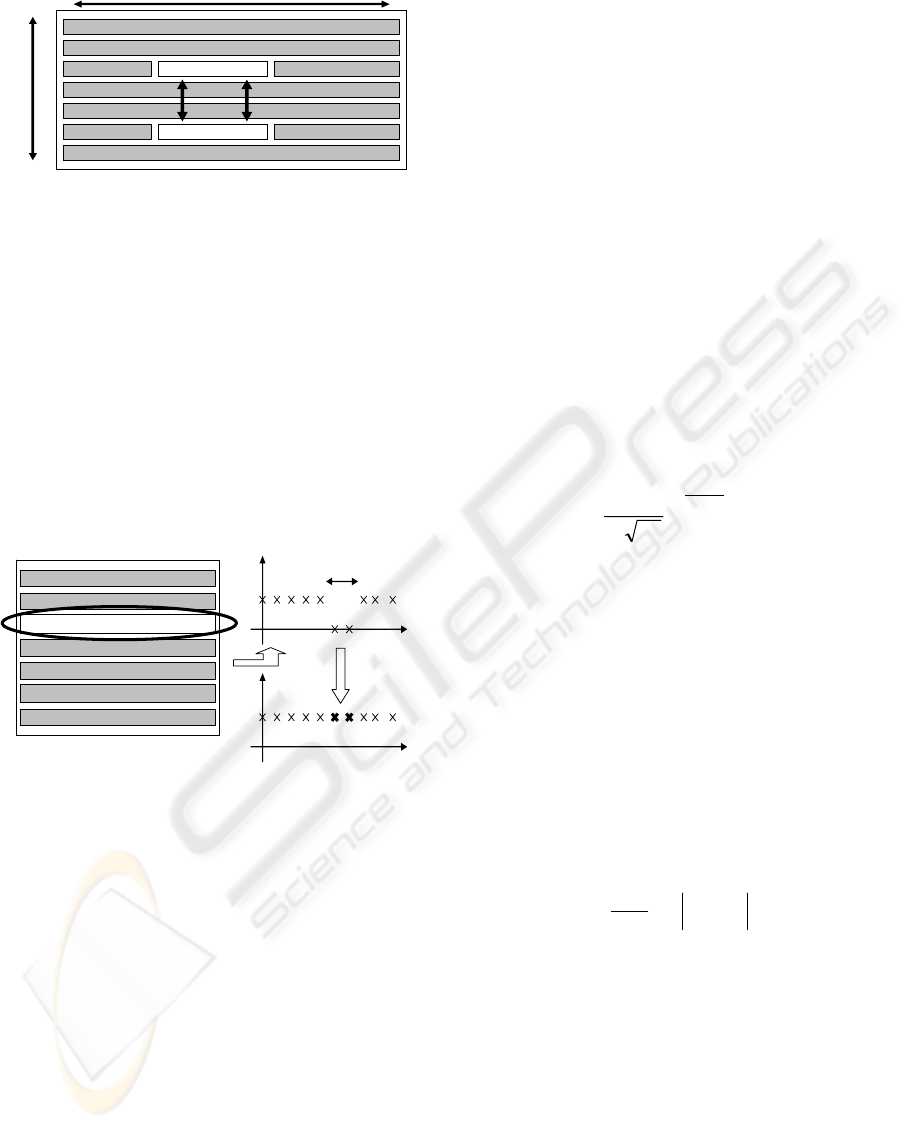
Figure 4: Exchange operator.
The second operator is an exchange operator,
introduced by (Kasarlis, et al., 1996). Some
production units are profitable or have larger
capacities. It may be interesting to exchange a part
of the planning of two production units (see fig. 4).
Finally, all-on and all-off operator are
introduced. Consider fig. 5. If the unit has a time
down constraints of two hours, it may be difficult to
go from feasible point a) to feasible point b). The
all-on (resp. all-off) operator randomly select two
time intervals and a production unit and switch on
(resp. switch off) the production unit between these
time intervals: the idea is to increase the probability
of “crossing the infeasible space”.
« All On »
2
=
down
T
1 1 1 1 1 1 1 0 0 1
a)
b)
Figure 5: All-on operator.
3.4 Continuous Ant Colony
Optimization for Produced Powers
Ant colony optimization was firstly introduced by
Marco Dorigo. Ants’ behaviour has been used as a
metaphor to design algorithms for combinatorial
optimization problems such as the Travelling
Salesman Problem (Dorigo, et al. 1997). Extensions
for continuous search spaces have been proposed by
(Socha and Dorigo, 2006) and have been used in
(Serban and Sandou, 2007) in a pure ant colony
solution of Unit Commitment. Results are here
called up. For each binary solution,
),,1;,,1;( KkNnuU
k
n
…… === , real values Q =
),,(),,1;,,1;(
1 KNk
n
xxKkNnQ ……… === have
to be associated. To compute these real variables, a
matrix
T of s real solutions, called “archive matrix
of solutions”, is stored:
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
KN
s
i
sss
KN
j
i
jjj
KNi
KNi
xxxx
xxxx
xxxx
xxxx
……



…
…
21
21
22
2
2
1
2
11
2
1
1
1
T .
(11)
These solutions are evaluated with respect to the
objective function (1). Costs are stored in
H:
[
]
T
sj
ffff ……
21
=H , with
()
.
u,uc
u,Qc
Q,Uff
N
n
K
k
k
n
k
n
k
off/on
k
n
k
n
k
prod
jjj
∑∑
==
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
==
11
1
)(
)(
(12)
The solutions are sorted according to their costs.
From these costs, weights are defined according to
the ranks of the solutions in the matrix. For the
solution with rank r, the weight is defined by:
()
.
2
1
22
2
2
1
sq
r
r
e
πqs
ω
−
−
=
(13)
Finally, a discrete probability distribution is
defined from these weights:
∑
=
=
s
j
jrr
p
1
/ ωω
(14)
q is a tuning parameter of the algorithm. To
compute a new real solution, the following
procedure is performed:
 a “model ant”, say l, is chosen, according to
this discrete probability distribution (14).
 Each real variable
i
new
x
, i = 1,…,KN, is
chosen with a Gaussian probability whose
mean and standard deviation is computed by:
.
xx
s
x
s
m
i
l
i
m
i
new
i
l
i
new
⎪
⎩
⎪
⎨
⎧
−
−
=
=
∑
=1
1
ξ
σ
μ
(15)
ξ is also a tuning parameter of the algorithm.
When real variables have been chosen, consumer’s
demands (5) may not be fulfilled. Furthermore, the
selection of produced powers may lead to
overproduction. To get rid of these problems, the
following improvement procedure is used:
 Select
k
n
Q with the previous algorithm.
 If
dem
n
K
k
k
n
k
n
QuQ >
∑
=1
(resp. < ), then
randomly choose, if possible, one of switched
on units, and decrease (resp. increase) the
corresponding produced power until
DISCRETE GENETIC ALGORITHM AND REAL ANT COLONY OPTIMIZATION FOR THE UNIT COMMITMENT
PROBLEM
259

dem
n
K
k
k
n
k
n
QuQ =
∑
=1
. If it is not sufficient,
choose several production units, if possible.
When all new solutions have been computed, the
best new solutions are stored in matrix
T, replacing
solutions whose costs were too high. This is an
analogy with physical evaporation of pheromone.
4 NUMERICAL RESULTS
4.1 Algorithm Implementation
The proposed cooperative method has been tested
with Matlab 6.5 with a Pentium IV 2.5 GHz. When
the stochastic cooperative algorithm is completed, a
final local search is performed: binary values are set
to their final values, and a real optimization based on
Semi Definite Programming is performed to solve
this particular economic dispatch problem. As
stochastic algorithms are considered, 70 tests are
performed, and statistical data about the results are
given. Optimization horizon is 24 hours with a
sampling time of one hour.
4.2 “4 unit” Academic Example
A 4 unit case is considered (see table 1).
Table 1: Characteristics for the “4 unit case”.
Q
min
(MW)
Q
max
(MW)
α
0
(€)
α
1
c
on
(€)
c
off
(€)
T
down
(h)
T
up
(h)
1 10 40 25 2.6 10 2 2 4
2 10 40 25 7.9 10 2 2 4
3 10 40 25 13.1 10 2 3 3
4 10 40 25 18.3 10 2 3 3
At time 0, all units are switched off and can be
switched on. Note that linear costs have been chosen
(α
2
= 0). For this relative small scale cases, and for
linear costs, an exact solution has been computed by
“Branch and Bound”. Consumer’s demand is
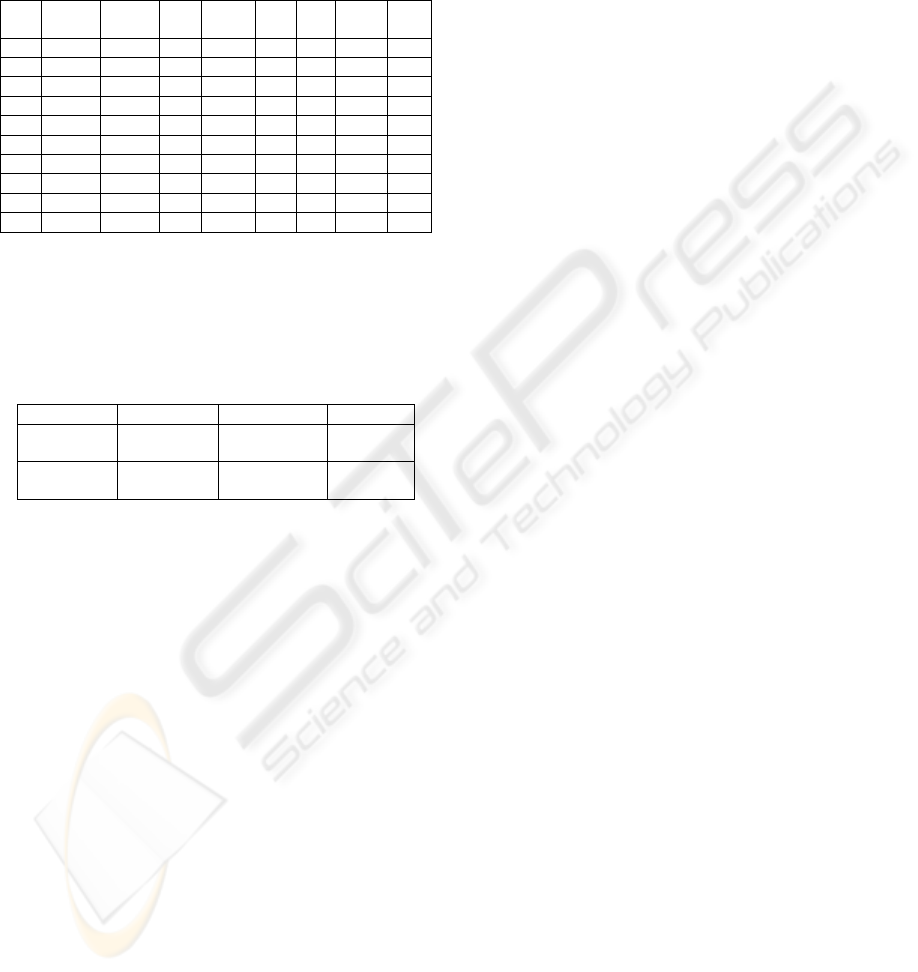
depicted in fig. 6. This demand can be fulfilled by 2
production units (see 2 units limit in fig. 6), except
for hour number 9. Because of time up constraints
this unit will be switched on for 3 hours. The
optimal solution is given in fig. 7.
The corresponding optimization problem is made
of 96 binary variables (24 hours and 4 units) and 96
real variables. Table 2 shows results of optimization.
Statistical results are given: best case, mean, number
of success (a test is successful if the best solution is
found).
The following parameters were used:
Figure 6: Consumer’s demand.
Figure 7: Optimal solution for “4 unit case”.
 Genetic population size: 50,
 Cross-over rate: 70%,
 Mutation rate: 5%,
 Knowledge based operators rate: 10%,
 Archive matrix size: s = 20,
 Tuning parameters 8.0;1 =
=
ξ
q .
Results show that interesesting solutions can be
computed with relatively low computation times.
Table 2: Optimization results “4 unit case”.
Case Best Mean Nb.
Success
Time
100 iter.
8778 €
(+0%)
9449 €
(+7.6%)
8/70 22 s
200 iter.
8778 €
(+0%)
9004 €
(+2.6%)
32/70 45 s
500 iter.
8778 €
(+0%)
8922 €
(+1.6%)
45/70 115 s
4.3 Medium Scale Case
A “10 unit” case is now considered (see table 3).
This a medium scale case. Low start up and start
down costs have been considered, leading to the
possibility of guessing the optimal solution. The
corresponding optimal cost is 29795 €. For a 24 hour
optimization, this problem is made of 240 binary
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
260

optimization variables and 240 real variables.
Results for the cooperative method are given in table
4. As in previous examples, 70 tests are performed
and statistical results are given (best case, mean).
The same values were used for parameters.
Table 3: Characteristics for the “10 unit case”.
Q
min
MW
Q
max
MW
α
0
€
α
1
c
on
€
c
off
€
T
dow
n
h
T
up
h
1 10 40 25 2.6 10 2 2 4
2 10 40 25 5.2 10 2 2 4
3 10 40 25 7.9 10 2 3 6
4 10 40 25 10.5 10 2 3 6
5 10 40 25 13.1 10 2 3 4
6 10 40 25 15.7 10 2 3 4
7 10 40 25 18.3 10 2 3 4
8 10 40 25 21.0 10 2 3 4
9 10 40 25 23.6 10 2 3 4
10 10 40 25 26.2 10 2 3 4
Results show the viability of the cooperative
method to solve mixed integer optimization
problems. Low computation times are observed,
even for this medium scale case.
Table 4: Optimization results “10 unit case”.
Best Mean Time
500 iter.
30210 €
(+1.4%)
32695 €
(+9.7%)
275 s
1000 iter.
29851 €
(+0.2%)
32138 €
(+7.8%)
550 s
5 CONCLUSION
In this paper, a cooperative method ant
colony/genetic algorithm for Unit Commitment
solution has been proposed. The main idea is to use
a genetic algorithm with knowledge based operators
to compute binary variables and a real ant colony
algorithm to compute real variables. To guarantee
the feasibility of the final solution, a criterion has
also been defined. Finally, the proposed method
leads to near optimal solutions, with guarantees of
feasibility and with low computation times.
Some dedicated methods are able to find better
solutions than the proposed cooperative algorithm,
and can consider larger scale cases. However, this
cooperative method seems to be promising and the
study has proven its viability.
Forthcoming works deal with the use of such a
cooperative metaheuristic method to solve generic
non linear mixed integer optimization problems, as
the use of the method does not require any structural
property of the problem.
REFERENCES
Chen C.-L and Wang S.-C. (1993), Branch and Bound
scheduling for thermal generating units, IEEE Trans.
on Energy Conversion, Vol. 8(2), pp.184-189.
Cheng C.-P., Liu C.-W., Liu C.-C. (2000), Unit
Commitment by Lagrangian Relaxation and Genetic
Algorithms, IEEE Trans. on Power Systems, Vol.
15(2), pp. 707-714.
Cheng C.-P., Liu C.-W., Liu C.-C. (2002), Unit
Commitment by annealing-genetic algorithm,
Electrical Power and Energy Systems, Vol. 24, pp.
149-158.
Dorigo M., Gambardella, L. M. (1997), Ant Colony
System: a Cooperative Learning Approach to the
Traveling Salesman Problem, IEEE Trans. on
Evolutionary Computation, Vol. 1, pp. 53-66.
Dotzauer E., Holmström K., Ravn H. F. (1999), Optimal
Unit Commitment and Economic Dispatch of
Cogeneration Systems with a Storage, Proceedings of
the 13
th
Power Systems Computation Conference 1999
PSCC’99, Trondheim, Norway, pp. 738-744.
Kasarlis S. A., Bakirtzis A. G. and Petridis V. (1996), A
genetic algorithm solution to the unit commitment
problem, IEEE Trans. on Power Systems, Vol. 11(1),
pp. 83-92.
Ouyang Z. and Shahidehpour S. M. (1991), An intelligent
dynamic programming for unit commitment
application, IEEE Trans. on Power Systems, Vol. 6(3),
pp. 1203-1209.
Purushothama G. K., Jenkins L. (2003), Simulated
annealing with local search – a hybrid algorithm for
Unit Commitment, IEEE Trans. on Power Systems,
Vol. 18(1), pp. 273-278.
Rajan C. C. A and Mohan M. R. (2004), An evolutionary
programming-based tabu search method for solving
the unit commitment problem, IEEE Trans. on Power
Systems, Vol. 19(1), pp. 577-585.
Sen S., Kothari D. P. (1998), Optimal Thermal Generating
Unit Commitment: a Review, Electrical Power &
Energy Systems, Vol. 20(7), pp. 443-451.
Senjyu T., Shimabukuro, K., Uezato K. and Funabashi T.
(2004), A fast technique for Unit Commitment
problem by extended priority list, IEEE Trans. on
Power Systems, Vol. 19(4), pp. 2119-2120.
Serban A. T, Sandou G. (2007), Mixed ant colony
optimisation for the Unit Commitment problem,
Lecture Notes in Computer Science, n°4431/4432, pp.
332-340.
Socha K., Dorigo M. (2006), Ant colony optimization for
continuous domains, Accepted to special issue of
EJOR on adapting metaheuristics to continuous
optimization.
Yin Wa Wong S. (1998), An Enhanced Simulated
Annealing Approach to Unit Commitment, Electrical
Power & Energy Systems, Vol. 20(5), pp. 359-368.
Zhai Q; and Guan X. (2002), Unit Commitment with
identical units: successive subproblems solving
method based on Lagrangian relaxation, IEEE Trans.
on Power Systems, Vol. 17(4), pp. 1250-1257.
DISCRETE GENETIC ALGORITHM AND REAL ANT COLONY OPTIMIZATION FOR THE UNIT COMMITMENT
PROBLEM
261