DIRECTIONAL MANIPULABILITY FOR MOTION

COORDINATION OF AN ASSISTIVE MOBILE ARM

K. Nait-Chabane, P. Hoppenot and E. Colle

IBISC Université d’Evry Val d’Essonne, 40 rue de plevoux 91020, Evry, France

Keywords: Mobile manipulator, manipulability, redundancy systems, robotic assistance.

Abstract: In this paper, we address the problem of coordinated motion control of a manipulator arm embarked on a

mobile platform. The mobile manipulator is used for providing assistance for disabled people. In order to

perform a given task by using mobile manipulator redundancy, we propose a new manipulability measure

that incorporates both arm manipulation capacities and the end-effector imposed task. This measure is used

in a numerical algorithm to solve system redundancy and then compared with other existing measures.

Simulation and real results show the benefit and efficiency of this measure in the field of motion

coordination.

1 INTRODUCTION

In assistive robotics, a manipulator arm constitutes

one possible solution for restoring some

manipulation functions to victims of upper limb

disabilities. The literature proposes three distinct

manipulator arm configurations. The first one

consists of a workstation in which a manipulator arm

evolves within a structured environment (RAID,

AFMASTER (Busnel, 2001)). In the second

configuration, a manipulator arm is added to an

electrical wheelchair ((Kwee, 1993), (Evers, 2001)).

The third configuration aims at expanding the field

of application of manipulator arm by making it

mobile, MoVAR (Van der Loos, 1995

), URMAD-

MOVAID (Dario, 1999) and ARPH (Hoppenot,

2002), that offers many advantages. Our research

deals with this third configuration. Such a system

possesses more degrees of freedom than necessary

for task execution. Any given point in the workspace

may be reached by moving the manipulator arm or

moving the mobile platform or by a combination of

both. To facilitate the use of the system by the

handicapped person, the idea is that the operator

pilots the gripper and that the remainder of the

articulated system follows. We have focused

attention on the use of redundancy for controlling a

mobile arm.

Manipulability measures play an important role

the design, analysis, evaluation and optimization

in manipulation robotics; it is a scalar that quantifies

how well the system behaves with respect to force

and motion transmission. These measures however

do not include information either on the task

imposed or on the direction of end-effector motion.

We propose an additional measure that takes the task

to be performed into account.

This paper is organized as follows. Section 2

prese

nts the work conducted towards devising

different solutions to the redundancy problem.

Section 3 discusses the mobile arm and its kinematic

models before Section 4 introduces the

manipulability concept and primary set of related

measures used in the literature on robotics. Section 5

then lays out a new measure that takes both the

system manipulation capacities and task in progress

into account. We will recall the principle behind the

kinematic control scheme used to solve redundancy

problems in Section 6, followed by an illustration of

the benefit of our new measure by means of

simulation and real results (in Section 7).

2 RELATED RESEARCH WORK

A considerable amount of interest has been shown

over the past few years in mobile manipulators.

Seraji (Seraji, 1993) presents a simple online

approach for the motion control of mobile

manipulators using augmented Jacobian matrices.

This kinematic approach requires additional

constraints to be satisfied for the manipulator

configuration. The approach proposed may be

201

Nait-Chabane K., Hoppenot P. and Colle E. (2007).

DIRECTIONAL MANIPULABILITY FOR MOTION COORDINATION OF AN ASSISTIVE MOBILE ARM.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 201-208

DOI: 10.5220/0001642402010208

 SciTePress

applied with equal ease to both nonholonomic and

holonomic mobile robots. Yamamoto and Yun

(Yamamoto, 1987) set out to decompose the motion

of the mobile manipulator into two subsystems

based on the concept of preferred operating region.

The mobile platform is controlled so as to bring the

manipulator into a preferred operating

region/configuration, with respect to the mobile

platform, as the manipulator performs a variety of

unknown manipulation tasks. The authors used the

manipulability measure of the manipulator arm to

define this preferred operating region. The principal

advantage of this approach lies in its decentralized

planning and control of the mobile platform and

manipulator arm. However, the case when the

manipulator is mounted at the center of the axis

between the two driving wheels lies at a singularity

in the method proposed by Yamamoto and Yun

(Yamamoto, 1987). Nagatani (Nagatani, 2002)

developed an approach to plan mobile base's path

which satisfies manipulator's manipulability. The

controllers used for manipulation and locomotion

differ from one another.

Khatib (Khatib, 1995) Khatib [10] proposed to

use a joint limit constraint in mobile manipulation in

the form of potential function while his approach is

to use the inherent dynamics characteristics of

mobile manipulator in operational space.

Additionally, he analyzed the inertial properties of a

redundant arm with macro-micro structure.

Kang (Kang, 2001) derived a combined potential

function algorithm to determine a posture satisfying

both the reduced inertia and joint limit constraints

for a mobile manipulator. The author then integrated

the inertia property algorithm into a damping

controller in order to reduce the impulse force upon

collision as well as to regulate contact.

Yoshikawa (Yoshikawa, 1990) introduced the

arm manipulators manipulability and used it to solve

the redundancy of such systems. The manipulability

of mobile manipulator has been studied by few

authors. Yamamoto and Yun (Yamamoto, 1999)

have treated both locomotion and manipulation

within the same framework from a task space

perspective. They have presented the kinematic and

dynamic contributions to manipulators and platforms

by means of the so-called task space ellipsoid.

Bayle (Bayle, 2001) extended the definition of

manipulability to the case of a mobile manipulator

and then applied it in an inversion process for

solving redundancy.

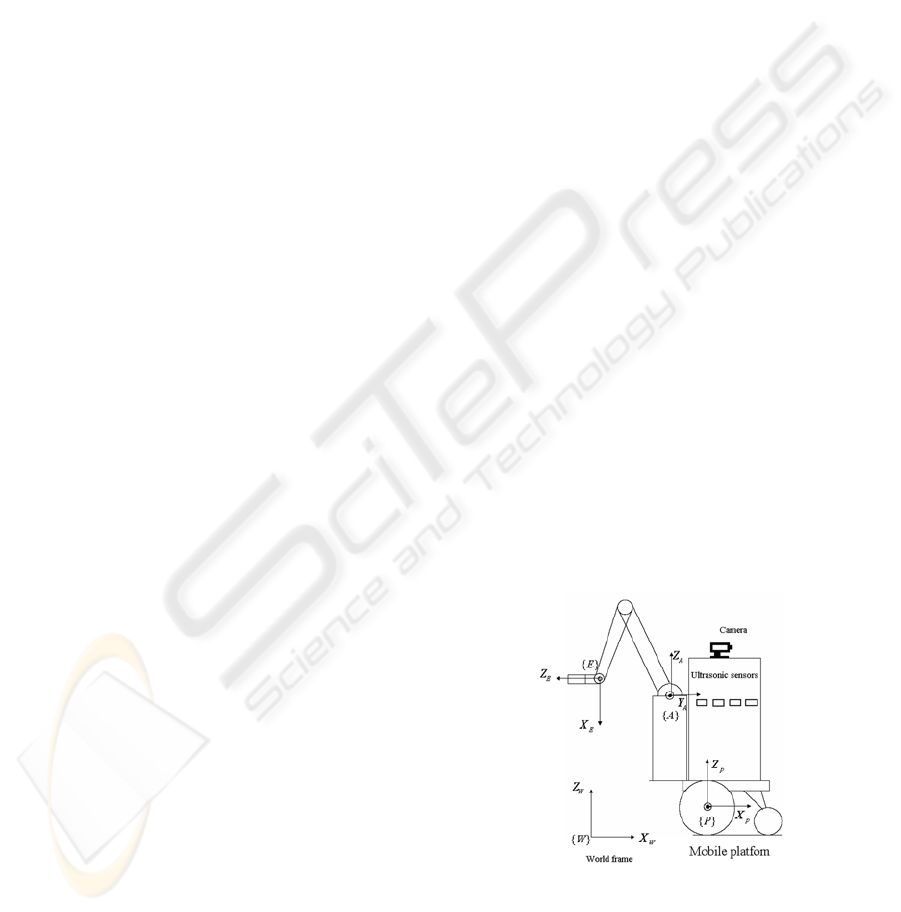
3 DESCRIPTION OF

ROBOTIZED ASSISTANT

The mobile manipulator consists of a Manus arm

mounted on a mobile platform powered by two

independent drive wheels. Let's start by defining a

fixed world reference frame {W}, a moving

platform frame {P} attached to the midway between

the two drive wheels, a moving arm frame {A}

related to the manipulator base, and a moving end-

effector frame {E} attached to the arm end-effector

(see Fig. 1).

We will adopt the following assumptions in

modeling the mobile manipulator system: no

slipping between wheel and floor; a platform

incapable of moving sideways in order to maintain

the nonholonomic constraint; and a manipulator

rigidly mounted onto the platform.

The forward kinematics of a serial chain manipulator

relating joint space and task space variables is

expressed by:

()

aaa

(1)

where

[, , ]

aaa am

xx x R=" ∈

∈

is the vector of

task variables in an m-dimensional task space,

is the vector of joint

variables in n-dimensional variables (called the

generalized coordinates), and f

[, , ]

aaa an

qqq q R="

is the nonlinear

function of the forward kinematic mapping

()

aaa

Jqq=



(2)

where



is the task velocity vector, the joint

velocity vector and



()

the Jacobian matrix.

Figure 1: Mobile manipulator system.

For the kinematic modeling of the considered

manipulator arm, we make use of Denavit-

Hartenberg parameters (Sciavicco, 1996). Manus

arm possesses six rotoid joints, with 3 DOF for

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

202

gripper positioning and 3 DOF for gripper

orientation. The Cartesian coordinates of the end-

effector relative to the arm base frame {A} are given

by:

1433212

2433212

34332

()-

()

Lc Lc c Ls

Lc Lc s Lc

xLsLs

⎧

⎪

=+ +

⎪

⎨

⎪

⎩

(3)

where

cos( ),

iai

cq= sin( )

iai

and

represent the length of shoulder, upper arm and

lower arm, respectively.

234

,,LLL

123

[, , ]

aa a

xxx

and

[,, ]

θψ

represent the Cartesian

coordinates and Euler angles of the end-effector,

respectively. In this paper, we will only consider the

three main joints of the arm, as given by the

generalized vector

123

[, , ]

aaaa

qqqq= .

The platform location is given by three

operational coordinates

and

, which

define its position and orientation. The generalized

coordinate vector is thus: and the

generalized velocity vector is:

[,,]

pppp

qxyθ=

[, , ]

pppp

qxy





The constraint equation applied to the platform

has the following form:

() 0

Aq q



(4)

in which

()[sin() cos()0]

pp p

=−

The kinematic model of the mobile platform is

given in (Campion, 1996):

()

qSqu=



⎥

(5)

where

and u

cos( ) 0

() sin()0

⎡⎤

⎢

⎢⎥

⎣⎦

= [v,ω]

, with v

and

ω being the linear and angular velocities of the

platform, respectively.

The forward kinematic model of the mobile

manipulator may be expressed in the following

form:

(, )

fq q=

(6)

where is the generalized coordinates of the

mobile platform and the joint variables of the

arm, as defined above.

The configuration of the mobile manipulator is

therefore defined by the

N generalized coordinates

(N=n+3):

[,] [, ,, ,, ]

TTT T

pa p ppa an

qqq xy q qθ== "

(7)

The direct kinematic model for the positioning

task of the considered mobile arm relative to world

frame

{W} is given by:

12 6

[, , , ] (, )

xx x fqq=="

(8)

12 1

22 1

()c()s

()s()c

pa a

ap p

xx x a bx

xy xa bx

xxc

θθ

ππ

θφθ

=+ + −−

=+ + +−

=+−=+−

⎧

⎪

⎨

⎪

⎩

(9)

where

cos( ),

sin( )

; a, b and c are

the Cartesian coordinates of the manipulator arm

base with respect to the mobile platform frame {P}.

The instantaneous kinematic model is then given

by:

()

Jqq=



(10)

with:

()

∂

We can observe that generalized velocities are

dependent; they are linked by the nonholonomic

constraint. The platform constraint described by (4)

can be written in the following form:



[( )0] 0

Aq q=



(11)

According to (5), the relation between the

generalized velocity vector of the system and its

control velocities can be written as follows:

()qMqu



(12)

DIRECTIONAL MANIPULABILITY FOR MOTION COORDINATION OF AN ASSISTIVE MOBILE ARM

203

where

()0

() .

⎡⎤

⎢⎥

⎣⎦

is an n-order identity matrix and

[, , , , ].

aan

uvwq q=



The instantaneous kinematic model does not

include the nonholonomic constraint of the platform

given by (11). The relationship between the

operational velocities of the mobile manipulator and

its control velocities takes the nonholonomic

platform constraint into account and may be

expressed by the reduced direct instantaneous

kinematic model, i.e.:

()

Jqu=



(13)

with:

() () ().

qJqMq=

4 MANIPULABILITY MEASURES

A well-established tool used for the motion analysis

of manipulators is known as the manipulability

ellipsoid approach. The concept of manipulability

was originally introduced by Yoshikawa

((Yoshikawa, 1985), (Yoshikawa, 1990)) for arm

manipulators, in order to denote a measure for the

ability of a manipulator to move in certain

directions. The set of all end-effector velocities that

may be attained by joint velocities such that the

Euclidean norm of ,



22 21/

(

aaa an

qqq q=++

 

)

satisfying

q ≤



is an ellipsoid in m-dimensional

Euclidean space. This ellipsoid represents the

manipulation capability and is called the

"manipulability ellipsoid".

Yoshikawa defines the manipulability measure w

as follows:

det(() ())

aaa a

wJqJq=

(14)

which can be simplified into

det( ( ))

wJq=

when

) is a square matrix.

Let's now consider the singular value

decomposition of

, as given by:

aaa

UV=∑

(15)

where and are orthogonal

matrices, and:

∈

⎡⎤

⎢⎥

Σ= ∈

⎢⎥

⎣⎦

(16)

in which:

aa am

σσ

≥≥≥"

The value of

aa am

σσ

is proportional

to the ellipsoid volume.

Another measure has been proposed for

characterizing the distance of a configuration from a

singularity (Salisbury, 1982). This measure is given

by:

(17)

where

and

are the maximum and minimum

singular values of the Jacobian matrix, respectively.

Bayle (Bayle, 2001) defined a measure w

that

extended the notion of eccentricity of the

ellipse, i.e.:

=−

(18)

The structure of the manipulator arm consists of an

arm portion with three joints and a wrist portion with

three joints whose axes intersect at a single point.

The arm portion concerns the positioning task, while

the wrist portion focuses on gripper orientation. It

proves quite useful to divide this study into wrist and

arm singularities. We present herein the

manipulability of the considered system for

positioning tasks.

5 DIRECTIONAL MEASURE

All of the abovementioned measures describe

system manipulability in general terms, without

taking the task the manipulator is being asked to

perform into account. One key factor behind the

failure of these measures is the fact that they do not

include information either on the task or on the

direction the end-effector is required to move. A

new measure should therefore be introduced to

address this situation.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

204

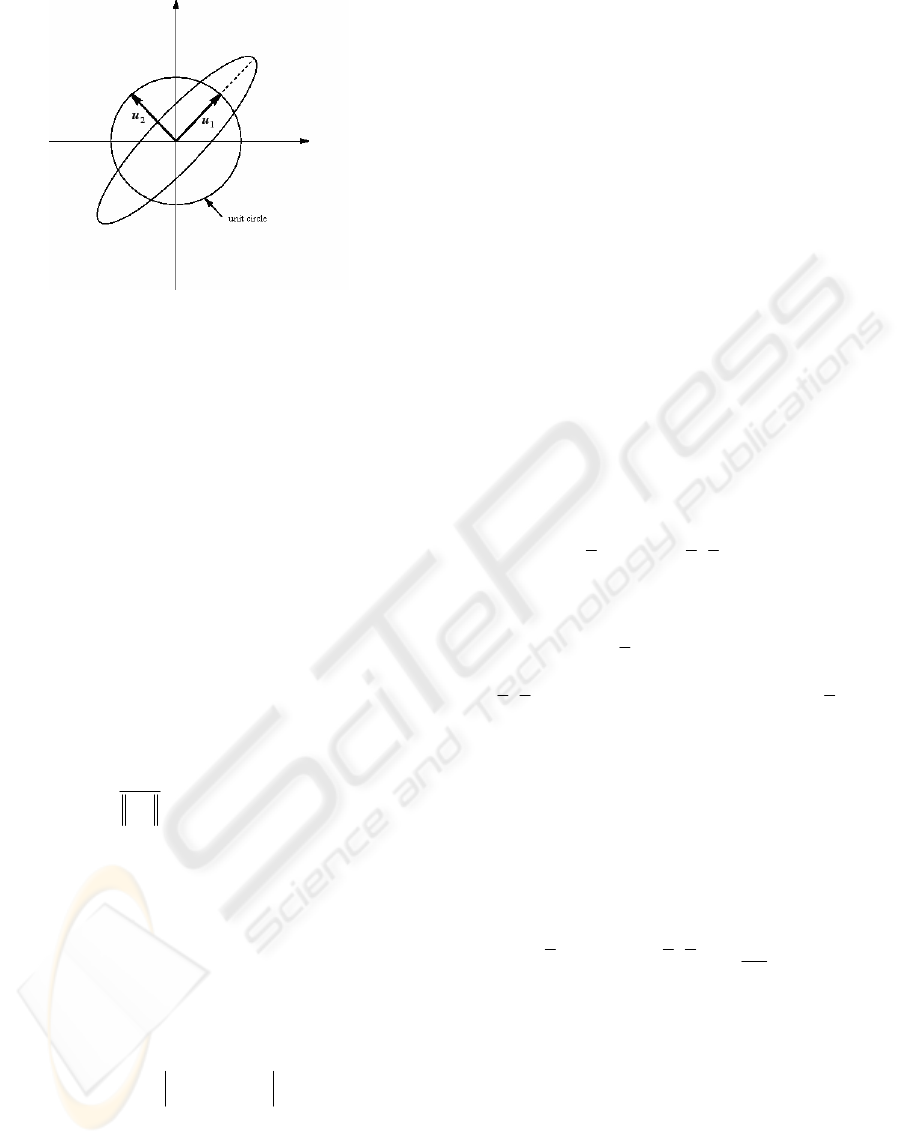
Figure 2: Manipulability ellipse in the two-dimensional

case.

The Singular Value Decomposition (15) of the

Jacobian matrix and its geometric relationship offer

further insights into characterizing the

manipulability of mechanical systems. Let

be the

column vector of U

. The primary axes of the

manipulability ellipsoid are then:

11 2 2

a a a a am am

uu u

σσ

. Figure 2 provides an

illustration of the two-dimensional case, according

to which

and u

yield the major and minor ellipse

axes, respectively. We propose to include

information on the direction of the task wished to

precisely know the manipulation capacity of the arm

manipulator for the execution of this operational

task.

Let



be the desired task. We now define a

unit vector



, which gives the direction of

the imposed task.

By using properties of the scalar product and the

singular values that represent radius of the ellipsoid,

we define a new manipulability measure as being the

sum of the absolute values of the scalar products of

the directional vector of the task by the singular

vectors pondered by their corresponding singular

values. This new measure is noted w

dir

(.)

dir ai ai

wdu

∑

(19)

This measure is maximized when the arm capacity

of manipulation according to the direction of the

task imposed is maximal. It is equal to zero if there

is no possibility of displacement according to this

direction.

6 CONTROL SCHEME

Whitney (Whitney, 1969) first proposed using the

pseudo-inverse of the manipulator Jacobian in order

to determine the minimum norm solution for the

joint rates of a serial chain manipulator capable of

yielding a desired end-effector velocity. A weighted

pseudo-inverse solution approach also allows

incorporating the various capabilities of different

joints, as discussed in Nakamura (Nakamura, 1991)

and Yoshikawa (Yoshikawa, 1984). One variant of

this approach includes superposition of the Jacobian

null space component on the minimum norm

solution to optimize a secondary objective

function (Baerlocher, 2001).

This same notion can then be extended to the

case of a nonholonomic mobile manipulator. The

inverse of the system given by equation (12) exhibits

the following form:

()

uJX IJJZ

=+−



(20)

where Z is a (N-1)-dimensional arbitrary vector.

The solution to this system is composed of both a

specific solution



that minimizes control

velocities norm and a homogeneous solution

(IJJZ

− )

belonging to the null space

()NJ

. By

definition, these latter added components do not

affect task satisfaction and may be used for other

purposes. For this reason, the null space is

sometimes called the redundant space in robotics.

The Z vector can be utilized to locally minimize

a scalar criterion. Along the same lines,

Bayle (Bayle,2001b) proposed the following

scheme:

()(

uJX WIJJM

∂

=−−

∂



)

(21)

where



is the desired task vector, W a positive

weighting matrix, and P(q) the objective function

dependent upon manipulator arm configuration. To

compare the advantage of our manipulability

measure with those presented in the literature, the

control scheme whose objective function depends on

various measures (

w, w

and w

) is to be applied.

For manipulation tasks involving a manipulator arm,

it is helpful to consider manipulability functions

DIRECTIONAL MANIPULABILITY FOR MOTION COORDINATION OF AN ASSISTIVE MOBILE ARM

205

whose minima correspond to optimal configurations,

e.g. (-w), (-w

) or w

As for the calculus, we used the numerical

gradient of P(q).

7 RESULTS

7.1 Simulation Results

In this section, we will consider a Manus arm

mounted on a nonholonomic mobile platform

described in Section 3. The mobile platform is

initially directed toward the positive X-axis at rest

=[0, 0, 0]

) and the initial configuration of the

manipulator arm is: q

= [4.71, 2.35, 4.19]

(rad).

The arm is fixed on the rear part of the platform. The

coordinates of the arm base with respect to the

platform frame are: [-0.12, -0.12, 0.4]

(m). The

imposed task consists of following a straight line

along a Y-axis of the world frame {W}. The velocity

along a path is constant and equal to 0.05 m.s

-1

Results obtained in the following cases have been

reported:

 in optimizing arm manipulability measure w;

 in optimizing arm manipulability measure w

dir

The comparison criteria are thus:

 Platform trajectory profile,

 indicator of energy spent E by the platform,

 manipulation capacity of the arm at the end of

the task, measured by w.

w is the most widely used indicator of

manipulability found in the literature. In our case, w

serves as a reference to evaluate the efficiency of the

control algorithm in terms of arm manipulability; its

values range between 0, which corresponds to

singular configurations, and 0.06, which corresponds

to good manipulability. In addition, we are looking

for forward displacements of the platform and

smooth trajectories. End-effector trajectories enable

checking if the task has been performed adequately.

E is defined by

vv=+

∑

, with v

and v

the

linear velocities respectively of the left and right

wheels of the platform.

Before presenting each case separately, it should

be noted that, for each one of them, the task is

carried out correctly.

Figure 3 shows simulation results in which arm

manipulability w is used as the optimizing criterion

for solving mobile arm redundancy. As depicted in

Figure 3a, the arm manipulability w quickly

improves up to a threshold corresponding to

acceptable configurations. Around 25 seconds, local

degradation of the manipulability measure is shown

to be quite low.

(a) (b)

Figure 3: Simulation result when optimizing arm

manipulability measure w.

To quickly improve arm manipulability while

performing the imposed task, the arm extends and

the platform retracts (see Fig. 3b). The platform

stops retracting once arm manipulability has been

optimized; afterwards, it advances so that the unit

carries out the imposed task. This evolution

corresponds to the first graining of the platform

trajectory. Since the platform is poorly oriented with

respect to the task direction, its contribution is

limited by the nonholonomic constraint, which does

cause slight degradation to the manipulability, as

shown in Figure 3a. The reorientation of the

platform, which corresponds to the second point of

graining, allows for improvement and optimization

of the manipulability measure. The mobile arm

achieves the desired task with an acceptable arm

configuration from a manipulation perspective; the

platform moves in reverse gear however, which

counters our intended aim. As there are two graining

points, the platform trajectory is not smooth. The

energy indicator E for this trajectory is E=7.15 m

-2

In Figure 4, we have used the proposed

directional manipulability of the arm to solve mobile

arm redundancy. Figure 4a shows the evolution of

the directional manipulability measure w

dir,

and arm

manipulability

w for comparison. The directional

manipulability of the arm is initially good; it

decreases slightly then improves progressively.

Corresponding measure w does not reach its

maximum value, but remains in a beach of

acceptable values, far from the singular

configurations. In this case, no local degradation of

the manipulability measure is detected. Figure 4b

presents the trajectory of the middle axis point on

the platform. This figure indicates that the mobile

platform retracts during a short period of time at the

very beginning in order to improve arm

manipulability. The platform reorients itself

according to the imposed task without changing its

motion direction. In executing a desired task, the

platform thus follows a smoother trajectory and

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

206

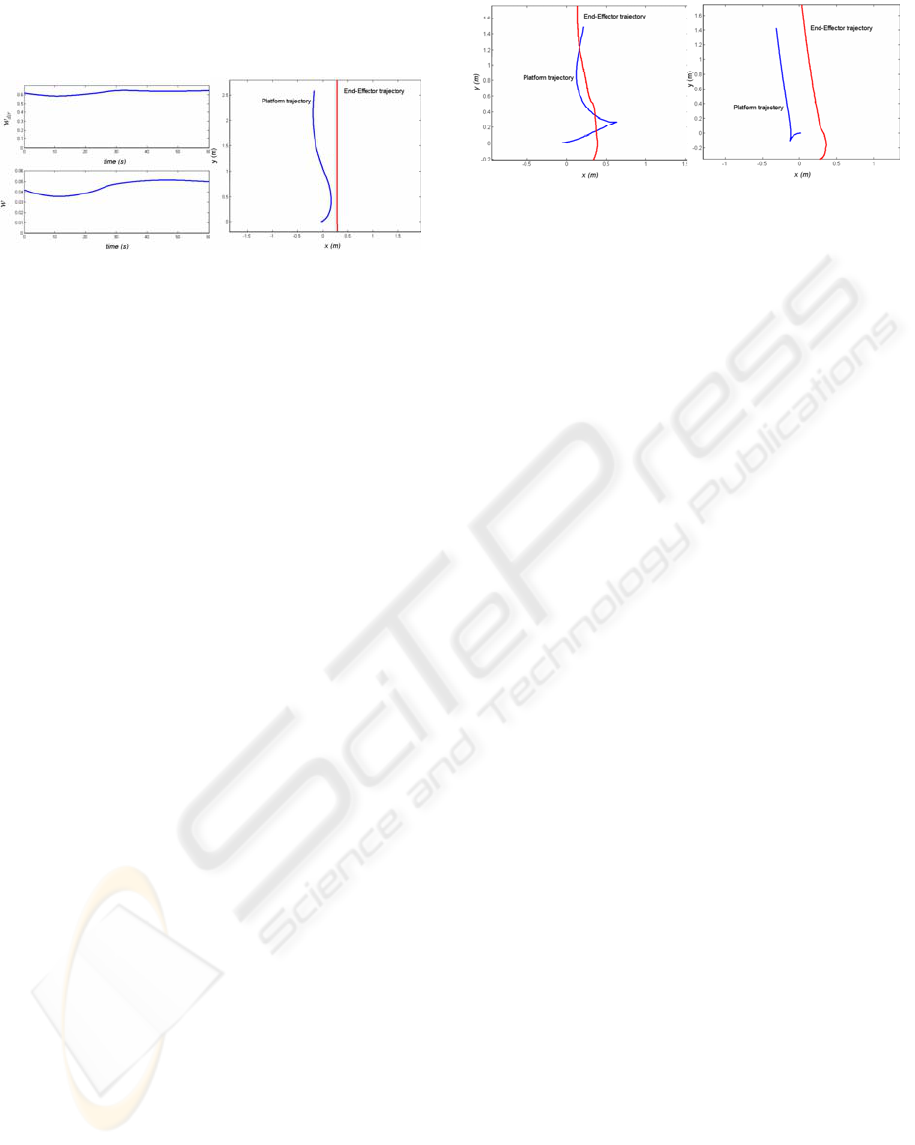
displays forward displacements. The energy

indicator E for this trajectory is E=3.1 m

-2

. Energy

expenditure is lower than the preceding case.

(a) (b)

Figure 4: Simulation result when optimizing arm

directional manipulability measure w

dir.

7.2 Results on Real System

To illustrate the results presented in theory, we

implemented on the real robot the algorithm.

Starting from a given configuration q

, collected by

the sensors data, we impose an operational task on

the end effector of the arm manipulator which

consists in following a straight line according to the

direction perpendicular to the axis longitudinal of

the platform (Y axis of the world frame). Imposed

velocity is 0.005 m per 60 ms cycle.

It should be noted that for each case, the task is

carried out correctly with good configuration from

manipulability point of view.

Figure 5 presents the platform and end effector

trajectories respectively in the cases of optimizing

arm manipulability w (figure 5a) and arm directional

manipulability w

dir

(figure 5b).

Platform and OT trajectories presented on Figure 5a

show that the platform carries out most part of its

movement in reverse gear. The end effector follows

a straight line with an error which reaches 21 cm in

end of the task. This error includes a set of

measurement errors and the tracking error.

In the case of directional manipulability

optimization, figure 5b indicates that the platform

moves back a little at the beginning and moves

according to the direction of the task. End-effector

follows a straight line with a weak error at the

beginning (less than 3cm) better than the case of the

optimization of w. The tracking error increases at the

end of the execution of the task. Indeed, as the

calculation of the gripper position is done on the

basis of odometric data, which generates not limited

errors, the tracking error increases.

(a) (b)

Figure 5: End-Effector and platform trajectories in the real

case.

7.3 Discussion

For all the cases studied, the task has been

performed adequately. The end-effector follows the

desired trajectory, as represented by a straight line

on the above figures. When a criterion is optimized,

manipulability is maintained up to a certain level.

Nevertheless, in the case of

w optimization, local

deteriorations are observed; these correspond to

graining points in the platform trajectories. In the

case of

optimization, local degradation does not

appear. Moreover, since

takes task direction into

account, the platform advances normally. The arm is

more heavily constrained by

, which adds a

supplementary condition on the task direction. The

platform seeks to replace the arm more quickly in

those configurations better adapted to following the

direction imposed by the task in progress.

This more natural behavior offers the advantage

of not disorienting the individual, an important

feature in assistive robotics, which calls for the robot

to work in close cooperation with the disabled host.

8 CONCLUSION

The purpose of this paper is to take advantage of

system redundancy in order to maximize arm

manipulability. Arm manipulability measures

serving as performance criteria within a real-time

control scheme make task execution possible with

the best arm configuration from manipulation ability

point of view. However, platform trajectories

contain graining points, especially when the system

is poorly-oriented with respect to the operational

task. The platform moves in reverse gear for the

most part of task execution. We have proposed a

new measure that associates information on task

direction with a manipulation capability measure. As

shown in the paper, thanks to the new criterion, the

imposed task is performed with human-like smooth

movements and good manipulation ability. Both

characteristics play an important part for

implementing efficient man machine cooperation.

DIRECTIONAL MANIPULABILITY FOR MOTION COORDINATION OF AN ASSISTIVE MOBILE ARM

207

The number of platform trajectory graining points is

reduced and, for the most part, the platform moves

forward.

Work in progress is focusing on the inclusion of

obstacle avoidance in the control scheme in order to

improve coordination between the two subsystems.

Another work relates to the development of a control

strategy for seizure. This strategy takes into account

both of human-machine cooperation and the

presence of obstacles in the environment.

REFERENCES

P. Baerlocher, “Inverse kinematics techniques for the

interactive posture control of articulated figures,” PhD

thesis, Lausanne, EPFL 2001.

B. Bayle, J.Y. Fourquet, M. Renaud, “Manipulability

Analysis for Mobile Manipulators,” In ICRA’2001,

Seoul, South Korea, pp. 1251-1256, May 2001.

B. Bayle, J. Y. Fourquet, M. Renaud. Using

Manipulability with Nonholonomic Mobile

Manipulators, 3rd International Conference on Field

and Service Robotics (FSR'2001), Helsinki (Finlande),

11-13 Juin 2001, pp.343-348

M. Busnel, R. Gelin and B. Lesigne, “Evaluation of a

robotized MASTER/RAID workstation at home:

Protocol and first results”, Proc. ICORR 2001, Vol. 9,

pp. 299-305, 2001.

G. Campion, G. Bastin and B. D’Andréa-Novel,

“Structural proprieties and classification of kinematic

and dynamic models of wheeled mobile robots,” IEEE

Transaction on Robotics and Automation, Vol. 12, no.

1, pp. 47-62, February 1996.

P. Dario, E. Guglielmelli, B. Allotta, “MOVAID: a

personal robot in everyday life of disabled and elderly

people,” Technology and Disability Journal, no 10,

IOS Press, 1999, pp. 77-93.

H. G. Evers, E. Beugels and G. Peters, “MANUS toward

new decade”, Proc. ICORR 2001, Vol. 9, pp. 155-161,

2001.

P. Hoppenot, E. Colle, “Mobile robot command by man-

machine co- operation - Application to disabled and

elderly people assistance,” Journal of Intelligent and

Robotic Systems, Vol. 34, no 3, pp 235-252, July

2002.

S. Kang, K. Komoriya, K. Yokoi, T. Koutoku, K. Tanie,

“Utilization of Inertial Effect in Damping-based

Posture Control of Mobile Manipulator,” International

Conference on Robotic and Automation, pp. 1277-

1282, Seoul, South Korea, May 2001.

O. Khatib, “Inertial properties in robotic manipulation: an

object-level framework,” Int J. Robotics Research,

Vol. 13, No. 1, pp. 19-36, 1995.

H. Kwee, C.A. Stanger, “The Manus robot arm”,

Rehabilitation Robotics News letter, Vol. 5, No 2,

1993.

K. Nagatani, T. Hirayama, A. Gofuku, Y. Tanaka,

“Motion planning for Mobile Manipulator with

keeping Manipulability,” IROS 2002, , pp 1663-1668,

Lausane, Switzerland, October 2002.

Y. Nakamura, “Advanced robotics, redundancy and

optimization,” Addison Wesley Publishing, 1991.

J. K. Salisbury and J.J. Craig, “Articulated hands: Force

Control and Kinematic Issues,” Intl. J. Robotics

Research, Vol. 1, no. 1, pp. 4-17, 1982.

L. Sciavicco and B. Siciliano, “Modeling and control of

robot manipulators,” The McGraw-Hill companies,

Inc., 1996.

H. Seraji, “An on-line approach to coordinated mobility

and manipulation,” In ICRA'1993, Atlanta, USA, May

1993, pp. 28-35.

D.E Whitney, “Resolved Motion Rate Control of

Manipulators and Human Prosthetics,” IEEE Trans on

Man Machine Systems, Vol 10, pp. 47-53, 1969.

Y. Yamamoto and X. Yun, “Coordinating locomotion and

manipulation of mobile manipulator,” Recent Trends

in Mobile Robots Zheng Y. Ed., 1987.

Y. Yamamoto and X. Yun, “Unified analysis an mobility

and manipulability of mobile manipulators,” IEEE Int.

Conf. Robotics and Automation, Detroit, pp. 1200-

1206, USA, 1999.

T. Yoshikawa, “Manipulability of Robotic Mechanisms,”

International Journal of Robotics Research, 1985, Vol.

4, no. 2, pp. 3-9.

Yoshikawa, T.: Foundation of robotics: Analysis and

control, The MIT Press, 1990.

T. Yoshikawa, “Analysis and control of Robot

manipulators with redundancy,” In M. Brady & R.

Paul, editors, Robotics Research: The First

International Symposium, MIT Press, pp. 735-747,

1984.

H.F.M. Van der Loos, “VA/Stanford Rehabilitation

Robotics Research and Development Program:

Lessons Learned in the Application of Robotics

Technology to the Field of Rehabilitation,” IEEE

Trans. Pn Rehabilitation Engineering, Vol. 3, n°1, pp.

46-55, March 1995.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

208