
FURTHER STUDIES ON VISUAL PERCEPTION FOR
PERCEPTUAL ROBOTICS
Ozer Ciftcioglu, Michael S. Bittermann
Delft University of Technology
I. Sevil Sariyildiz
Delft University of Technology
Keywords: Vision, visual attention, visual perception, perception measurement.
Abstract: Further studies on computer-based perception by vision modelling are described. The visual perception is
mathematically modelled, where the model receives and interprets visual data from the environment. The
perception is defined in probabilistic terms so that it is in the same way quantified. At the same time, the
measurement of visual perception is made possible in real-time. Quantifying visual perception is essential
for information gain calculation. Providing virtual environment with appropriate perception distribution is
important for enhanced distance estimation in virtual reality. Computer experiments are carried out by
means of a virtual agent in a virtual environment demonstrating the verification of the theoretical
considerations being presented, and the far reaching implications of the studies are pointed out.
1 INTRODUCTION
Visual perception, although commonly articulated in
various contexts, it is generally used to convey a
cognition related idea or message in a quite fuzzy
form and this may be satisfactory in many instances.
Such usage of perception is common in daily life.
However, in professional areas, like computer
vision, robotics, or design, its demystification or
precise description is necessary for proficient
executions. Since the perception concept is soft and
thereby elusive, there are certain difficulties to deal
with it. For instance, how to quantify it or what are
the parameters, which play role in visual perception.
Visual perception is one of the important
information sources playing role on human’s
behavior. Due to the diversity of existing approaches
related to perception, which emerged in different
scientific domains, we provide a comprehensive
introduction to be explicit as to both, the objectives,
and the contribution of the present research.
Perception has been considered to be the
reconstruction a 3-dimensional scene from 2-
dimensional image information (Marr, 1982;
Poggio, Torre et al., 1985; Bigun, 2006). This image
processing approach attempts to mimic the
neurological processes involved in vision, with the
retinal image acquisition as starting event. However,
modeling the sequence of brain processes is a
formidable endeavor. This holds true even when
advanced computational methods are applied for
modeling of the individual brain-components’
behavior (Arbib, 2003). The reason is the brain
processes are complex.
Brain researchers trace visual signals as they are
processed in the brain. A number of achievements
are reported in the literature (Wiesel, 1982; Hubel,
1988; Hecht-Nielsen, 2006). However, due to
complexity there is no consensus about the exact
role of brain regions, sub-regions and individual
nerve-cells in vision, and how they should be
modeled (Hecht-Nielsen, 2006; Taylor, 2006). The
brain models are all different due to the different
focus of attention that refers to uncountable number
of modalities in the brain. Therefore they are
inconclusive as to understanding of a particular
brain process like perception on a common ground.
As a state of the art, they try to form a firm clue for
perception and attention beyond their verbal
accounts. In modeling the human vision the
involved brain process components as well as their
interactions should be known with certainty if a
468
Ciftcioglu O., S. Bittermann M. and Sevil Sariyildiz I. (2007).
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 468-477
DOI: 10.5220/0001642504680477
Copyright
c
SciTePress

deterministic approach, like the image processing
approach, is to be successful. This is currently not
the case. Well-known observations of visual effects,
such as depth from stereo disparity (Prince, Pointon
et al., 2002), Gelb effect (Cataliotti and Gilchrist,
1995), Mach bands (Ghosh, Sarkar et al., 2006),
gestalt principles (Desolneux, Moisan et al., 2003),
depth from defocus (Pentland, 1987) etc. reveal
components of the vision process, that may be
algorithmically mimicked. However, it is unclear
how they interact in human vision to yield the
mental act of perception. When we say that we
perceived something, the meaning is that we can
recall relevant properties of it. What we cannot
remember, we cannot claim we perceived, although
we may suspect that corresponding image
information was on our retina. With this basic
understanding it is important to note that the act of
perceiving has a characteristic that is uncertainty: it
is a common phenomenon that we overlook items in
our environment, although they are visible to us, i.e.,
they are within our visual scope, and there is a
possibility for their perception. This everyday
experience has never been exactly explained. It is
not obvious how some of the retinal image data does
not yield the perception of the corresponding objects
in our environment. Deterministic approaches do not
explain this common phenomenon.
The psychology community established the
probable “overlooking” of visible information
experimentally (Rensink, O’Regan et al., 1997;
O’Regan, Deubel et al., 2000), where it has been
shown that people regularly miss information
present in images. For the explanation of the
phenomenon the concept of visual attention is used,
which is a well-known concept in cognitive sciences
(Treisman and Gelade, 1980; Posner and Petersen,
1990; Itti, Koch et al., 1998; Treisman, 2006).
However, it remains unclear what attention exactly
is, and how it can be modeled quantitatively. The
works on attention mentioned above start their
investigation at a level, where basic visual
comprehension of a scene must have already
occurred. An observer can exercise his/her bias or
preference for certain information within the visual
scope only when he/she has already a perception
about the scene, as to where potentially relevant
items exist in the visible environment. This early
phase, where we build an overview/initial
comprehension of the environment is referred to as
early vision in the literature, which is omitted in the
works on attention mentioned above. While the
early perception process is unknown, identification
of attention in perception, that is due to a task
specific bias, is limited. This means, without
knowledge of the initial stage of perception its
influence on later stages is uncertain, so that the
later stages are not uniquely or precisely modeled
and the attention concept is ill-defined. Since
attention is ill-defined, ensuing perception is also
merely ill-defined. Some examples of definitions on
perception are “Perception refers to the way in
which we interpret the information gathered and
processed by the senses,” (Levine and Sheffner,
1981) and “Visual perception is the process of
acquiring knowledge about environmental objects
and events by extracting information from the light
they emit or reflect,” (Palmer, 1999). Such verbal
definitions are helpful to understand what perception
is about; however they do not hint how to tackle the
perception beyond qualitative inspirations. Although
we all know what perception is apparently, there is
no unified, commonly accepted definition of it.
As a summary of the previous part we note that
visual perception and related concepts have not been
exactly defined until now. Therefore, the perception
phenomenon is not explained in detail and the
perception has never been quantified, so that the
introduction of human-like visual perception to
machine-based system remains as a soft issue.
In the present paper a newly developed theory of
perception is introduced. In this theory visual
perception is put on a firm mathematical foundation.
This is accomplished by means of the well-
established probability theory. The work
concentrates on the early stage of the human vision
process, where an observer builds up an unbiased
understanding of the environment, without
involvement of task-specific bias. In this sense it is
an underlying fundamental work, which may serve
as basis for modeling later stages of perception,
which may involve task specific bias. The
probabilistic theory can be seen as a unifying theory
as it unifies synergistic visual processes of human,
including physiological and neurological ones.
Interestingly this is achieved without recourse to
neuroscience and biology. It thereby bridges from
the environmental stimulus to its mental realization.
Through the novel theory twofold gain is
obtained. Firstly, the perception and related
phenomena are understood in greater detail, and
reflections about them are substantiated. Secondly,
the theory can be effectively introduced into
advanced implementations since perception can be
quantified. It is foreseen that modeling human visual
perception can be a significant step as the topic of
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
469

perception is a place of common interest that is
shared among a number of research domains,
including cybernetics, brain research, virtual reality
computer graphics, design and robotics (Ciftcioglu,
Bittermann et al., 2006). Robot navigation is one of
the major fields of study in autonomous robotics
(Oriolio, Ulivi et al., 1998; Beetz, Arbuckle et al.,
2001; Wang and Liu, 2004). In the present work, the
human-like vision process is considered. This is a
new approach in this domain, since the result is an
autonomously moving robot with human-like
navigation to some extent. Next to autonomous
robotics, this belongs to an emerging robotics
technology, which is known as perceptual robotics
(Garcia-Martinez and Borrajo, 2000; Söffker, 2001;
Burghart, Mikut et al., 2005; Ahle and Söffker,
2006; Ahle and Söffker, 2006). From the human-
like behaviour viewpoint, perceptual robotics is
fellow counterpart of emotional robotics, which is
found in a number of applications in practice
(Adams, Breazeal et al., 2000). Due to its merits, the
perceptual robotics can also have various
applications in practice.
From the introduction above, it should be
emphasized that, the research presented here is
about to demystify the concepts of perception and
attention as to vision from their verbal description to
a scientific formulation. Due to the complexity of
the issue, so far such formulation is never achieved.
This is accomplished by not dealing explicitly with
the complexities of brain processes or neuroscience
theories, about which more is unknown than known,
but incorporating them into perception via
probability. We derive a vision model, which is
based on common human vision experience
explaining the causal relationship between vision
and perception at the very beginning of our vision
process. Due to this very reason, the presented
vision model precedes all above referenced works in
the sense that, they can eventually be coupled to the
output of the present model.
Probability theoretic perception model having
been established, the perception outcome from the
model is implemented in an avatar-robot in virtual
reality. The perceptual approach for autonomous
movement in robotics is important in several
respects. On one hand, perception is very
appropriate in a dynamic environment, where
predefined trajectory or trajectory conditions like
occasional obstacles or hindrances are duly taken
care of. On the other hand, the approach can better
deal with the complexity of environments by
processing environmental information selectively.
The organization of the paper is as follows.
Section two gives the description of the perception
model developed in the framework of ongoing
perceptual robotics research. Section three describes
a robotics application. This is followed by
discussion and conclusions.
2 A PROBABILISTIC THEORY
OF VISUAL PERCEPTION
2.1 Perception Process
We start with the basics of the perception process
with a simple and special, yet fundamental
orthogonal visual geometry. It is shown in figure 1.
P
l
l
o
y
y
0
y
Figure 1: The geometry of visual perception from a top
view, where P represents the position of eye, looking at a
vertical plane with a distance l
o
to the plane; f
y
(y) is the
probability density function in y-direction.
In figure 1, the observer is facing and looking at a
vertical plane from the point denoted by P. By
means of looking action the observer pays visual
attention equally to all locations on the plane in the
first instance. That is, the observer visually
experiences all locations on the plane without any
preference for one region over another. Each point
on the plane has its own distance within the
observer’s scope of sight which is represented as a
cone. The cone has a solid angle denoted by
θ
. The
distance of a point on the plane and the observer is
denoted by l and the distance between the observer
and the plane is denoted by l
o
. Since visual
perception is associated with distance, it is
straightforward to proceed to express the distance of
visual perception l in terms of
θ
and l
o
. From figure
1, this is given by
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
470
)cos(
θ
o
l
l =
(1)
Since we consider that the observer pays visual
attention equally to all locations on the plane in the
first instance, the probability of getting attention for
each point on the plane is the same so that the
associated probability density function (pdf) is
uniformly distributed. This positing ensures that
there is no visual bias at the beginning of visual
perception as to the differential visual resolution
angle d
θ
. Assuming the scope of sight is defined by
the angle
θ
=
±
π
/2, the pdf f
θ
is given by
π
θ
1
=f
(2)
since
θ
is a random variable, the distance x in (1) is
also a random variable. The pdf f
l
(l) of this random
variable is computed as (Ciftcioglu, Bittermann et
al.)
22
2
)(
o
o
l
lll
l
lf
−
=
π
(3)
for the interval
∞
≤≤ ll
o
.
Considering that
o
l
y
tg =θ)(
(4)
and by means of pdf calculation similar to that to
obtain f
x
(x) one can obtain f
y
(y) as (Ciftcioglu,
Bittermann et al.).
)(
)(
22
o
o
y
yl
l
yf
+π
=
(5)
for the interval
∞
≤
≤∞− y
. (9) and (11) are dual
representation of the same phenomenon. The
probability density functions f
l
(l) and f
y
(y) are
defined as attention in the terminology of cognition.
By the help of the results given by (9) and (11)
two essential applications in design and robotics are
described in a previous research (Bittermann,
Sariyildiz et al.). In this research the fundamental
orthogonal visual geometry is extended to a general
visual geometry to explore the further properties of
the perception phenomenon. In this geometry the
earlier special geometry the orthogonality condition
of the infinite plane is relaxed. This geometry is
shown in figure 2 where the attentions at the points
O and O’ are subject to computation, with the same
axiomatic foundation of the probabilistic theory, as
before. Since the geometry is symmetrical with
respect to x axis, we consider only the upper domain
of the axis without loss of the generality.
x
(x, y)
(x
o
, y
o
)
P
l
o
O
y
r
l
1
l
2
h
O
'
s
r
r
Figure 2: The geometry of visual perception where the
observer has the position at point
P with the orientation to
the point
O. The x,y coordinate system has the origin
placed at
O and the line defined by the points P and O
coincides with the
x axis for the computational
convenience.
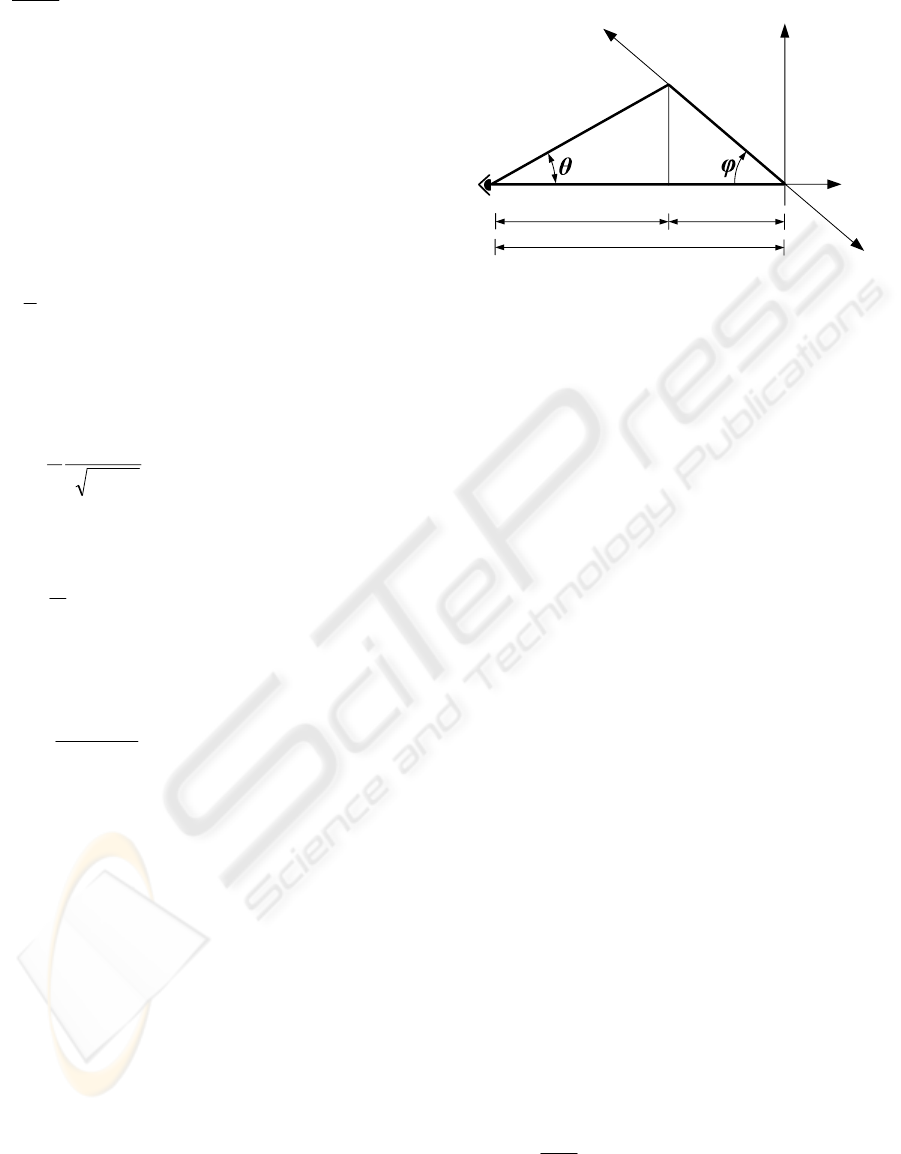
In figure 2, an observer at the point P is viewing an
infinite plane whose intersection with the plane of
page is the line passing from two point designated as
O and O’. O represents the origin. The angle
between OO’ and OP is designated as
θ
. The angle
between OP and OO’ is defined by φ. The distance
between P and O’ is denoted by s and the distance
of O’ to the OP line is designated as h. The distance
of O’ to O is taken as a random variable and denoted
by r. By means of looking action the observer pays
visual attention equally in all directions within the
scope of vision. That is, in the first instance, the
observer visually experiences all locations on the
plane without any preference for one region over
another. Each point on the plane has its own
distance within the observer’s scope of sight which
is represented as a cone. The cone has a solid angle
denoted by
θ
. The distance between a point on the
plane and the observer is denoted by l and the
distance between the observer and the plane is
denoted by l
o
. Since we consider that the observer
pays visual attention equally for all directions within
the scope of vision, the associated probability
density function (pdf) with respect to θ is uniformly
distributed. Positing this ensures that there is no
visual bias at the beginning of visual perception as
to the differential visual resolution angle d
θ
.
Assuming the scope of sight is defined by the angle
θ
= +
π
/2, the pdf f
θ
is given by
2/
1
π
θ
=f
(6)
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
471
Since
θ
is a random variable, the distance r in (1) is
also a random variable. The pdf f
r
(r) of this random
variable is computed as follows.
To find the pdf of the variable r denoted f
r
(r) for a
given r we consider the theorem on the function of
random variable and, following Papoulis (Papoulis),
we solve the equation
r= g(
θ
)
(7)
for
θ
in terms of r. If
θ
1
,
θ
2
,….,
θ
n
, .. are all its
real roots,
r=g(
θ
1
) = g(
θ
2
) =……= g(
θ
n
) = ….
Then
..
|)('|
)(
...
|)('|
)(
...
|)('|
)(
)(
2
2
1
1
+++++=
n
n
r
g
f
g
f
g
f
rf
θ
θ
θ
θ
θ
θ
θθθ
(8)
Aiming to determine f
r
(r) given by (8), from figure 2
we write
1
l
h
θtg =
θtg
h
l
1
=
(9)
2
l
h
φtg =
φtg
h
l
2
=
(10)
o21
l
φtg
h
θtg
h
ll =+=+
(11)
From above, we solve h, which is
φtg
1
θtg
1
l
h
o
+
=
(12)
From figure 2, we write
()
ϕ
ϕ
sin
h
r =
(13)
Using (12) in (13), we obtain
() ()
ϕθ
θ
ϕ
θ
ϕ
ϕ
tgtg
tg
l
g
l
r
oo
+
==
+
=
sin
tgφ
tgφ
1
tgθ
1
1
sin
(14)
We take the derivative w.r.t.
θ
, which gives
()
()
()
2
22
o
φtgθtg
θtg
θcos
1
φtgθtg
θcos
1
φsin
tgφl
θ'g
+
−+
=
(15)
()
2
2
o
φtgθtg
θcos
1
φtg
φsin
tgφl
+
=
(16)
Substituting tg(θ) from (14) into (16) yields
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
ϕ
=
+
ϕ
=
θ
=θ
1
2
2
o
1
2
1
2
2
o
2
2
o
1
θtg
1
1r
l
θtg
θtg1
r
l
r
1
l
inφs
g
sin
sin
sin
'
(17)
Above, tg(
θ
1
) is computed from (14) as follows.
We apply the theorem of function of random
variable (Papoulis):
)(g'
)(f
(r)f
1
1r
r
θ
θ
=
(21)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
1
2
2
o
r
θtg
1
1r
l
sinφ
2
π
1
(r)f
(22)
where
ϕϕ
tg
r
l
r
t
o
−
=
sin
gθ
1
(23)
Substitution of (23) into (22) gives
2
2
sin
sin
2
1
)(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
=
ϕϕ
ϕ
π
tg
r
l
r
l
rf
o
o
r
(24)
or
2
2
cos2
)sin(
2
)(
oo
o
r
lrlr
l
rf
+−
=
ϕ
ϕ
π
(25)
for
.
)cos(ϕ
<<
0
l
r0
(26)
To show (25) is a pdf, we integrate it in the interval
given by (26). The second degree equation at the
denominator of (25) gives
)(sin ϕ−=−
22
o
2
l4ac4b
θ
ϕ
ϕ
ϕθ
tg
tgl
tgrtgr
o
sin
=+
(18)
ϕθ
ϕ
ϕ
tgrtg
tg
lr
o
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
sin
(19)
r
tgl
tgr
tg
o
−
=
ϕ
ϕ
ϕ
θ
sin
1
(20)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
472
where b=2l
o
r and a=1 and c=l
o
2
, so that
ac4b
2
<
which means, for this the integral
∫
=
)cos(/
0
0
),(
ϕ
ϕ
l
r
drrfI
(27)
gives (Korn and Korn)
1|}
)sin(
)cos(
{
2/
1
)cos(/
=
−
=
ϕ
ϕ
ϕ
π
o
l
o
o
o
l
lr
arctgI
(28)
as it should verify as pdf. Since attention is a scalar
quantity per unit, it has to be the same for different
geometries subjected to computation meaning that it
is measured with the same units in both cases. In the
same way we can say that since perception is a
scalar quantity, the perceptions have to be
correspondingly the same. Referring to both the
orthogonal geometry and the general geometry, the
density functions are shown in figure 3a. The same
attention values at the origin O are denoted by p
o
.
Since the attentions are the same, for the perception
comparison, the attention values have to be
integrated within the same intervals in order to
verify the same quantities at the same point. Figure
3b is the magnified portion of figure 3a in the
vicinity of origin. In this magnified sketch the
infinitesimally small distances dy and dr are
indicated where the relation between dy and dr is
given by dy =dr sin(
ϕ
) or
dr=dy/sin(
ϕ
)
(29)
and
dr
lrlr
l
drrf
oo
o
r
2
2
cos2
)sin(
2
)(
+−
=
ϕ
ϕ
π
(30)
substitution of (29) into (30) yields
x
f
r
(r)=
*
f
r
(r)
sin
P
O
y
r
O
'
r
l
o
r
)y(f
y
O
'
p
p
O
p
O
x
P
O
y
r
r
dy
(a) (b)
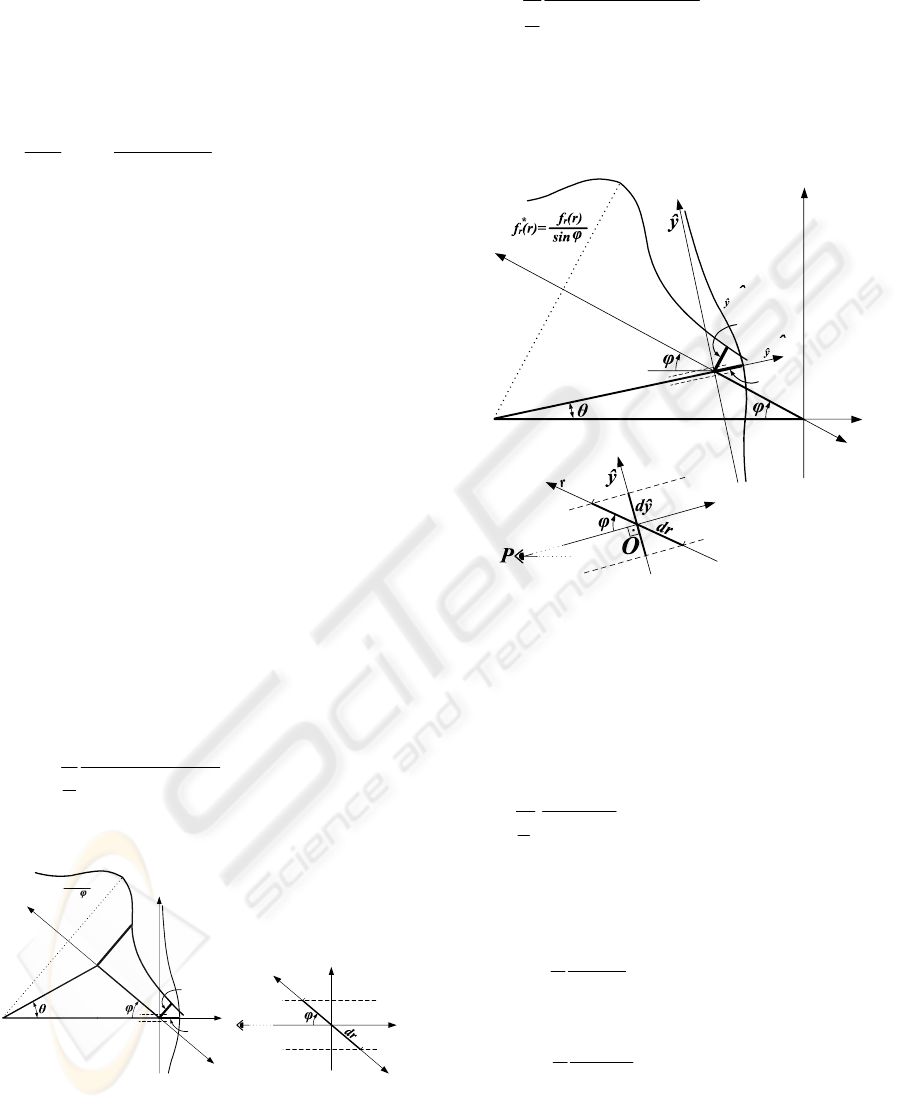
Figure 3: Illustration of the perception in the orthogonal
geometry and the general geometry indicating the
relationship between the infinitesimally small distances
dy and dr. The geometry (a) and zoomed region at the
origin (b).
2
2
*
cos2
1
2
)(
oo
o
r
lrlr
l
rf
+−
=
ϕ
π
(31)
which is the attention for a general geometry. It
boils down into the orthogonal geometry for all
conditions; for a general position of O’ within the
visual scope, this is illustrated in figure 4 as this was
already illustrated in figure 3 for the origin O.
O
O
'
r
r
l
o
P
p
O'
p
O'
f
(y)
f
(y)
y
x
Figure 4: Illustration of the perception in the orthogonal
geometry and the general geometry indicating the
relationship between the infinitesimally small distances dŷ
and dr. This is the same as figure 3 but the zoomed region
is at a general point denoted by O’.
The pdf has several interesting features. First, for
ϕ
=
π
/2, it boils down
()
2
o
2
o
y
lr
1
2
π
l
(r)f
+
=
(32)
An interesting point is that when
ϕ→
0 but r
≠
0. This
means O’ is on the gaze line from P to O. For the
case O’ is between P and O, f
r
(r) becomes
2
)(
1
)(
rl
l
rf
o
o
r
−
=
π
(33)
or otherwise
2
)(
1
)(
rl
l
rf
o
o
r
+
=
π
(34)
In (33) for r
→
l
0
f
r
(r)
→∞
. This case is similar to
that in (3) where l
→
l
0
f
l
(l)
→∞
.
The variation of f
r
*
(r,
ϕ
) is shown in figure 5 in a 3-
dimensional plot where
ϕ
is a parameter.
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
473

Figure 5: The variation of f
r
*
(r,
ϕ
) is shown as a 3-
dimensional plot for l
o
=5.
The actual f
r
(r) is obtained as the intersection of a
vertical plane passing from the origin O and the
surface. The analytical expression of this
intersection is given by (25) and it is shown in figure
4 where
ϕ
is a parameter; for the upper plot
ϕ
=π/4 and for the lower plot
ϕ
=π/2. The latter
corresponds to the vertical cross section of the
surface shown in figure 3 as lower plot.
P
r
O
s
r
l
o
)y,x(
-5 0 5
0
0.05
0.1
0.15
0.2
-5 0 5
0.03
0.04
0.05
0.06
0.07
0.08
Figure 6: The pdf f
r
(r,
ϕ
) where
ϕ
is a parameter; for the
upper plot
ϕ
=π/4 and for the lower plot
ϕ
=π/2.
The pdf in (25) indicates the attention variation
along the line r in figure 2 where the observer faces
the point O.
3 APPLICATION
Presently, the experiments have been done with the
simulated measurement data since the
multiresolutional filtering runs in a computationally
efficient software platform which is different than
the computer graphics platform of virtual reality.
For the simulated measurement data, first the
trajectory of the virtual agent is established by
changing the system dynamics from the straight
ahead mode to bending mode for a while, three
times. Three bending modes are seen in figure 7
with the complete trajectory of the perceptual agent.
The state variables vector is given by
],,,,[
ω
•
•
= yyxxX
where
ω
is the angular rate and it is estimated during
the move. When the robot moves in a straight line,
the angular rate becomes zero.
In details, there are three lines plotted in figure 7.
The green line represents the measurement data set.
The black line is the extended Kalman filtering
estimation at the highest resolution of the perception
measurement data. The outcome of the
multiresolutional fusion process is given with the
blue line. The true trajectory is indicated in red. In
this figure they cannot be explicitly distinguished.
For explicit illustration of the experimental
outcomes the same figure with a different zooming
range and the zooming power are given in figures 8
and 9 for bending mode and 10 for a straight-ahead
case. From the experiments it is seen that, the
Kalman filtering is effective for estimation of the
trajectory from perception measurement. Estimation
is improved by the multiresolutional filtering.
Estimations are relatively more accurate in the
straight-ahead mode.
-2000 -1500 -1000 -500 0 500 1000
-
2000
-
1500
-
1000
-500
0
trajectory ref [r], MDF [b], EKF [k] and measurements [g]
Figure 7: Robot trajectory, measurement, Kalman
filtering and multiresolutional filtering estimation.
It is noteworthy to mention that, the
multiresolutional approach presented here uses
calculated measurements in the lower resolutions. In
general case, each sub-resolution can have separate
perception measurement from its own dedicated
perceptual vision system for more accurate
executions. The multiresolutional fusion can still be
improved by the use of different data acquisition
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
474

provisions which play the role of different sensors at
each resolution level and to obtain independent
information subject to fusion.
Figure 8: Enlarged Robot trajectory, measurement Kalman
filtering and multiresolutional filtering estimation, in
bending mode (light grey is for measurement, the smooth
line is the trajectory).
Figure 9: Enlarged Robot trajectory, measurement Kalman
filtering and multiresolutional filtering estimation, in
bending mode (light grey is for measurement, the smooth
line is the trajectory).
4 DISCUSSION AND
CONCLUSION
Although, visual perception is commonly articulated
in various contexts, generally it is used to convey a
cognition related idea or message in a quite fuzzy
form and this may be satisfactory in many instances.
Such usage of perception is common in daily life.
However, in professional areas, like architectural
design or robotics, its demystification or precise
description is necessary for proficient executions.
Since the perception concept is soft and thereby
elusive, there are certain difficulties to deal with it.
For instance, how to quantify it or what are the
parameters, which play role in visual perception.
The positing of this research is that perception is a
very complex process including brain processes. In
fact, the latter, i.e., the brain processes, about which
our knowledge is highly limited, are final, and
therefore they are most important. Due to this
complexity a probabilistic approach for a visual
perception theory is very much appealing, and the
results obtained have direct implications which are
in line with our common visual perception
experiences, which we exercise every day.
Figure 10: Enlarged Robot trajectory, measurement
Kalman filtering and multiresolutional filtering estimation
in straight-ahead mode (light grey is for measurement, the
smooth line is the trajectory).
In this work a novel theory of visual perception is
developed, which defines perception in probabilistic
terms. The probabilistic approach is most
appropriate, since it models the complexity of the
brain processes, which are involved in perception
and result in the characteristic uncertainty of
perception, e.g., an object may be overlooked
although it is visible. Based on the constant
differential angle in human vision, which is the
minimal angle humans can visually distinguish,
vision is defined as the ability to see, that is, to
receive information, which is transmitted via light,
from different locations in the environment, which
are located within different differential angles. This
ability is modeled by a function of a random
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
475

variable, namely the viewing direction, which has a
uniform probability density for the direction, to
model unbiased vision in the first instance. Hence
vision is defined as probabilistic act. Based on
vision, visual attention is defined as the
corresponding probability density with respect to
obtaining information from the environment.
Finally, the visual perception is the intensity of
attention, which is the integral of attention over a
certain unit length, yielding a probability that the
environmental information from a region in the
environment is realized in the brain.
It is noteworthy to emphasize that perception is to
be expressed in terms of intensity, which is the
integral of a probability density. This is not
surprising since perception, corresponding to its
commonly understood status as a mental event,
should be a dimensionless quantity, as opposed to a
concept, which involves a physical unit, namely a
probability density over a unit length, like visual
attention. The definitions are conforming to
common perception experience by human. The
simplicity of the theory in terms of understanding its
result together with its explanatory power, indicates
that a fundamental property of perception has been
identified.
In this theory of perception a clear distinction is
made between the act of perceiving and seeing.
Namely, seeing is a definitive process, whereas
perception is a probabilistic process. This distinction
may be a key to understand many phenomena in
perception, which are challenging to explain from a
deterministic viewpoint. For example the theory
explains the common experience, that human beings
may overlook an object while searching for it,
although such an overlooking is not justified, and it
is difficult to explain the phenomenon. This can be
understood from the viewpoint that vision is a
probabilistic act, where there exists a chance that
corresponding visual attention is not paid
sufficiently for the region in the environment, which
would provide the pursued information. An
alternative explanation, which is offered by an
information theoretic interpretation of the theory, is
that through the integration of the visual attention
over a certain domain some information may be lost,
so that, although attention was paid to a certain item
in the environment, pursued information is not
obtained. The theory also explains how it is
possible, that different individuals have different
perceptions in the same environment. Although
similar viewpoints in the same environment have
similar visual attention with unbiased vision, the
corresponding perception remains a phenomenon of
probability, where a realization in the brain is not
certain, although it may be likely.
The theory is verified by means of extensive
computer experiments in virtual reality. From visual
perception, other derivatives of it can be obtained,
like visual openness perception, visual privacy,
visual color perception etc. In this respect, we have
focused on visual openness perception, where the
change from visual perception to visual openness
perception is accomplished via a mapping function
and the work is reported in another publication
(Ciftcioglu, Bittermann et al.). Such perception
related experiments have been carried out by means
of a virtual agent in virtual reality, where the agent
is equipped with a human-like vision system
(Ciftcioglu, Bittermann et al.).
Putting perception on a firm mathematical
foundation is a significant step with a number of far
reaching implications. On one hand vision and
perception are clearly defined, so that they are
understood in greater detail, and reflections about
them are substantiated. On the other hand tools are
developed to employ perception in more precise
terms in various cases and even to measure
perception. Applications for perception
measurement are architectural design, where they
can be used to monitor implications of design
decisions, and autonomous robotics, where the robot
moves based on perception (Ciftcioglu, Bittermann
et al.).
REFERENCES
Adams, B., C. Breazeal, et al., 2000. Humanoid robots: a
new kind of tool, Intelligent Systems and Their
Applications, IEEE [see also IEEE Intelligent
Systems] 15(4): 25-31.
Ahle, E. and D. Söffker, 2006. A cognitive-oriented
architecture to realize autonomous behaviour – part I:
Theoretical background. 2006 IEEE Conf. on Systems,
Man, and Cybernetics, Taipei, Taiwan.
Ahle, E. and D. Söffker, 2006. A cognitive-oriented
architecture to realize autonomous behaviour – part II:
Application to mobile robots. 2006 IEEE Conf. on
Systems, Man, and Cybernetics, Taipei, Taiwan.
Arbib, M. A., 2003. The Handbook of Brain Theory and
Neural Networks. Cambridge, MIT Press.
Beetz, M., T. Arbuckle, et al., 2001. Integrated, plan-
based control of autonomous robots in human
environments, IEEE Intelligent Systems 16(5): 56-65.
Bigun, J., 2006. Vision with direction, Springer Verlag.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
476

Bittermann, M. S., I. S. Sariyildiz, et al., 2006. Visual
Perception in Design and Robotics, Integrated
Computer-Aided Engineering to be published.
Burghart, C., R. Mikut, et al., 2005. A cognitive
architecture for a humanoid robot: A first approach.
2005 5th IEEE-RAS Int. Conf. on Humanoid Robots,
Tsukuba, Japan.
Cataliotti, J. and A. Gilchrist, 1995. Local and global
processes in surface lightness perception, Perception
& Psychophysics 57(2): 125-135.
Ciftcioglu, Ö., M. S. Bittermann, et al., 2006.
Autonomous robotics by perception. SCIS & ISIS
2006, Joint 3
rd
Int. Conf. on Soft Computing and
Intelligent Systems and 7
th
Int. Symp. on advanced
Intelligent Systems, Tokyo, Japan.
Ciftcioglu, Ö., M. S. Bittermann, et al., 2006. Studies on
visual perception for perceptual robotics. ICINCO
2006 - 3rd Int. Conf. on Informatics in Control,
Automation and Robotics, Setubal, Portugal.
Ciftcioglu, Ö., M. S. Bittermann, et al., 2006. Towards
computer-based perception by modeling visual
perception: a probabilistic theory. 2006 IEEE Int.
Conf. on Systems, Man, and Cybernetics, Taipei,
Taiwan.
Desolneux, A., L. Moisan, et al., 2003. A grouping
principle and four applications, IEEE Transactions on
Pattern Analysis and Machine Intelligence 25(4): 508-
513.
Garcia-Martinez, R. and D. Borrajo, 2000. An integrated
approach of learning, planning, and execution, Journal
of Intelligent and Robotic Systems 29: 47-78.
Ghosh, K., S. Sarkar, et al., 2006. A possible explanation
of the low-level brightness-contrast illusions in the
light of an extended classical receptive field model of
retinal ganglion cells, Biological Cybernetics 94: 89-
96.
Hecht-Nielsen, R., 2006. The mechanism of thought.
IEEE World Congress on Computational Intelligence
WCCI 2006, Int. Joint Conf. on Neural Networks,
Vancouver, Canada.
Hubel, D. H., 1988. Eye, brain, and vision, Scientific
American Library.
Itti, L., C. Koch, et al., 1998. A model of saliency-based
visual attention for rapid scene analysis, IEEE Trans.
on Pattern Analysis and Machine Intelligence 20(11):
1254-1259.
Korn, G. A. and T. M. Korn, 1961. Mathematical
handbook for scientists and engineers. New York,
McGraw-Hill.
Levine, M. W. and J. M. Sheffner, 1981. Fundamentals of
Sensation and Perception. London, Addison-Wesley.
Marr, D., 1982. Vision, Freeman.
O’Regan, J. K., H. Deubel, et al., 2000. Picture changes
during blinks: looking without seeing and seeing
without looking, Visual Cognition 7: 191-211.
Oriolio, G., G. Ulivi, et al., 1998. Real-time map building
and navigation for autonomous robots in unknown
environments, IEEE Trans. on Systems, Man and
Cybernetics - Part B: Cybernetics 28(3): 316-333.
Palmer, S. E., 1999. Vision Science. Cambridge, MIT
Press.
Papoulis, A., 1965. Probability, Random Variables and
Stochastic Processes. New York, McGraw-Hill.
Pentland, A., 1987. A new sense of depth, IEEE Trans. on
Pattern Analysis and Machine Intelligence 9: 523-531.
Poggio, T. A., V. Torre, et al., 1985. Computational vision
and regularization theory, Nature 317(26): 314-319.
Posner, M. I. and S. E. Petersen, 1990. The attention
system of the human brain, Annual Review of
Neuroscience 13: 25-39.
Prince, S. J. D., A. D. Pointon, et al., 2002. Quantitative
analysis of the responses of V1 Neurons to horizontal
disparity in dynamic random-dot stereograms, J
Neurophysiology 87: 191-208.
Rensink, R. A., J. K. O’Regan, et al., 1997. To see or not
to see: The need for attention to perceive changes in
scenes, Psychological Science 8: 368-373.
Söffker, D., 2001. From human-machine-interaction
modeling to new concepts constructing autonomous
systems: A phenomenological engineering-oriented
approach., Journal of Intelligent and Robotic Systems
32: 191-205.
Taylor, J. G., 2006. Towards an autonomous
computationally intelligent system (Tutorial). IEEE
World Congress on Computational Intelligence WCCI
2006, Vancouver, Canada.
Treisman, A. M., 2006. How the deployment of attention
determines what we see, Visual Cognition 14(4): 411-
443.
Treisman, A. M. and G. Gelade, 1980. A feature-
integration theory of attention, Cognitive Psychology
12: 97-136.
Wang, M. and J. N. K. Liu, 2004. Online path searching
for autonomous robot navigation. IEEE Conf. on
Robotics, Automation and Mechatronics, Singapore.
Wiesel, T. N., 1982. Postnatal development of the visual
cortex and the influence of environment (Nobel
Lecture), Nature 299: 583-591.
FURTHER STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
477
