
An Improved Architecture for Cooperative and
Comparative Neurons (CCNs) in Neural Network
Md. Kamrul Islam
School of Computing, Queen’s University
Kingston, K7L 3N6, ON, Canada
Abstract. The ability to store and retrieve information is critical in any type of
neural network. In neural network, the memory particularly associative memory,
can be defined as the one in which the input pattern leads to the response of
a stored pattern (output vector) that corresponds to the input vector. During the
learning phase the memory is fed with a number of input vectors that it learns and
remembers and in the recall phase when some known input is presented to it, the
network exactly recalls and reproduces the required output vector. In this paper,
we improve and increase the storing ability of the memory model proposed in
[1]. Besides, we show that there are certain instances where the algorithm in [1]
does not produce the desired performance by retrieving exactly the correct vec-
tor from the memory. That is, in their algorithm, a number of output vectors can
become activated from the stimulus of an input vector while the desired output is
just a single correct vector. We propose a simple solution that overcomes this and
can uniquely and correctly determine the output vector stored in the associative
memory when an input vector is applied. Thus we provide a more general sce-
nario of this neural network memory model consisting of memory element called
Competitive Cooperative Neuron (CCN).
1 Introduction
The ability to store and retrieve information is critical in any type of neural network. In
neural network, the memory, particularly associative memory, can be defined as the one
in which the input pattern or vector leads to the response of a stored pattern (output vec-
tor) that corresponds to the input vector. That is, when an input vector is presented, the
network recalls the corresponding output vector associated with the input vector. There
are two types of associative memories: autoassociative and heteroassociative memory.
In the case of autoassociative memory, both input and output vectors range over the
same vector space. For example, a spelling corrector maps incorrectly spelled words
(e.g “matual”) to correctly spelled words (“mutual”). Heteroassociation involves the
mapping between input and output vectors over a different vector space. For example,
given a name (“John”) as input, the system will be able to recall its corresponding
phone number (“657 − 9876”) stored in memory.
In the context of neural network, an associative memory consists of neurons (known
as conventional McCulloh-Pitts [7] neurons) that are capable of processing input vector
and recalling output vector. These conventional model neurons use inputs from each
Kamrul Islam M. (2007).
An Improved Architecture for Cooperative and Comparative Neurons (CCNs) in Neural Network.
In Proceedings of the 3rd International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 48-55
DOI: 10.5220/0001642900480055
Copyright
c
SciTePress

source that are characterized by the amplitude of input signals. In this way each neuron
can receive, process, and recall only one component of a memorized vector. Towards
realizing the concept of associative memory, one of the commonly used techniques uses
correlation matrix memory [3] which encodes all input and output vector pairs {y
k
, x
T
k
}
(k = 1, 2, 3 · · · , n) into a correlation matrix M =
P
n
k=1
y
k
x
T
k
. Later in the recall
phase the matrix M is decoded to extract the output vector when the corresponding
input vector is introduced to the network. The limitation of correlation matrix memory,
in terms of memory capacity, is that it requires exactly n neurons to recall n components
of a vector. In this paper we study the problem of increasing memory storage and recall
capacity of a general associative memory and offer an idea that provides and ensures
more storage and correct recall ability of the memory model (one layer Competitive
Cooperative Neuron (CCN) network model) proposed in [1]. Our proposed method
improves the architecture of the CCN network where we need only N neurons (CCNs)
to store and recall NR memories where R is the number of zones (defined later) of a
CCN.
The organization of the paper is as follows. First in section 2, we provide the general
description of a competitive cooperative neuron (CCN), In section 3 we show how a
network of such neurons can be formed and how they work by demonstrating with
an example. Our main results, that is, the improvement of the CCN network model are
given in section 5 which overcomes shortcomings of the model [1] (discussed in section
4). We conclude in section 6.
2 Description of a CCN
Here we provide the concise description of the CCN, the reader is referred to [1] for de-
tails. In order to increase memory storage and recall capacity of an associative memory
compared to correlation matrix memory, the paper [1] introduces a novel type of model
neuron called competitive and cooperative neuron (CCN) as the building block of an
associative memory. This model offers two new aspects: One is that the input signals
are characterized by a two-dimensional (2-D) parameter set representing the amplitude
and frequency of signals. The other aspect of the CCN is that the neuron receives input
signals at several distinct and autonomous receptor zones. A model of a CCN is given
in Fig. 1.
The CCN consists of a number of zones R and each zone r ∈ R collects in-
put from many sources, S(r) = {S
1
(r), S
2
(r), S
3
(r) · · · }. Each input signal (source)
S
i
(r) = (F
i
(r), A
i
(r)) has two aspects- the frequency F
i
(r) ∈ [0, 1] which encodes
the information [4] and the amplitude A
i
(r) ∈ [0, 1]-the strength of the signal. Each
zone is sensitive to a small range of frequencies (band). The center of the band of input
r of a CCN n at time t is denoted by B(n, r, t) and the tolerance level is T (n, r, t).
After each attempt to learn a specific memory, a band that is sufficiently close to the
winning signal is preserved when the CCN fires. A zone accepts the input if the fre-
quencies that are within its band and the amplitude of it exceeds a certain threshold
τ(n, r, t) ∈ [0, 1]. That is, a signal wins if A
i
(r) ≥ τ (n, r, t) > 0 and F
i
(r) ∈
[B(n, r, t) − T (n, r, t), B(n, r, t) + T (n, r, t)]. Each input zone propagates the win-
ning signal to the cell body. Finally, the CCN fires if the combined amplitude of the
49

max
cell body
Winning input from
zone R
Winning input from zone 1
w
1
w
m
Fig.1. A CCN Model: the CCN on the left has five autonomous zones, each of which has a narrow
bandwidth of frequencies that it can detect. Each zone receives m input signals. In each zone, only
the input signals that have a frequency f
i,r
that falls within the zone’s badwidth participate in the
competition and the winner is the signal with the highest effective amplitude. All the winning
signals are propagated to the cell’s body, where they cooperate and the cell is activated if the
cumulative amplitude is greater than the cell’s threshold.
winning input signals from all the zones exceeds the threshold v(n, t) of the CCN
body, that is,
P
R
r=1
A(i(r ) ≥ v(n, t). As the CCN is activated (fired) it sets the cen-
ter of the frequency band of an active zone r to its corresponding winning signal, i.e.,
B(n, r, t) = F
i(w)
(r). In our case, as the CCN fires we determine the output vector
of it whose components are the winning signals of all the zones of the CCN. Also, the
output vector can be changed by using Hebbian learning [5] protocol. Initially, we start
with a CCN body threshold v(n, t), which is greater than or equal to the sum of the
zone thresholds, i.e., v(n, t) ≥
P
r
τ(n, r, t), so that in order for the CCN to fire, either
all the zones must be active or some of them must receive a very strong signal.
When fired, the CCN decreases tolerance levels in contributing zones where the
tolerance level is the maximum value of the difference between the band and the win-
ning signal frequency that results in the firing. This is the situation when we say the
CCN specializes or learns. During training, the CCN also decreases the threshold for
the amplitude in active zones and also decreases the threshold of the CCN body which
allows for a clean but weaker signal to activate a zone. When the CCN is trained and
it receives input in some but not all zones it uses that input to recall the previous in-
puts to the idle zones. For example [1], if a CCN has three zones and it fired when
the input was the vector that represents the triple (Red, Sweet, Strawberry), then the
next time it receives only “Red” and no input from the other zones, it will fire (“Red”,
“Sweet”,“Strawberry”) provided that the amplitude of the input signal (“Red”) exceeds
the cell’s threshold.
2.1 CCN Network Model
A simple one-layer feedforward network with three CCNs and three input sources is
shown in Fig. 2. Each CCN has three receptor zones represented by the vertices of the
50
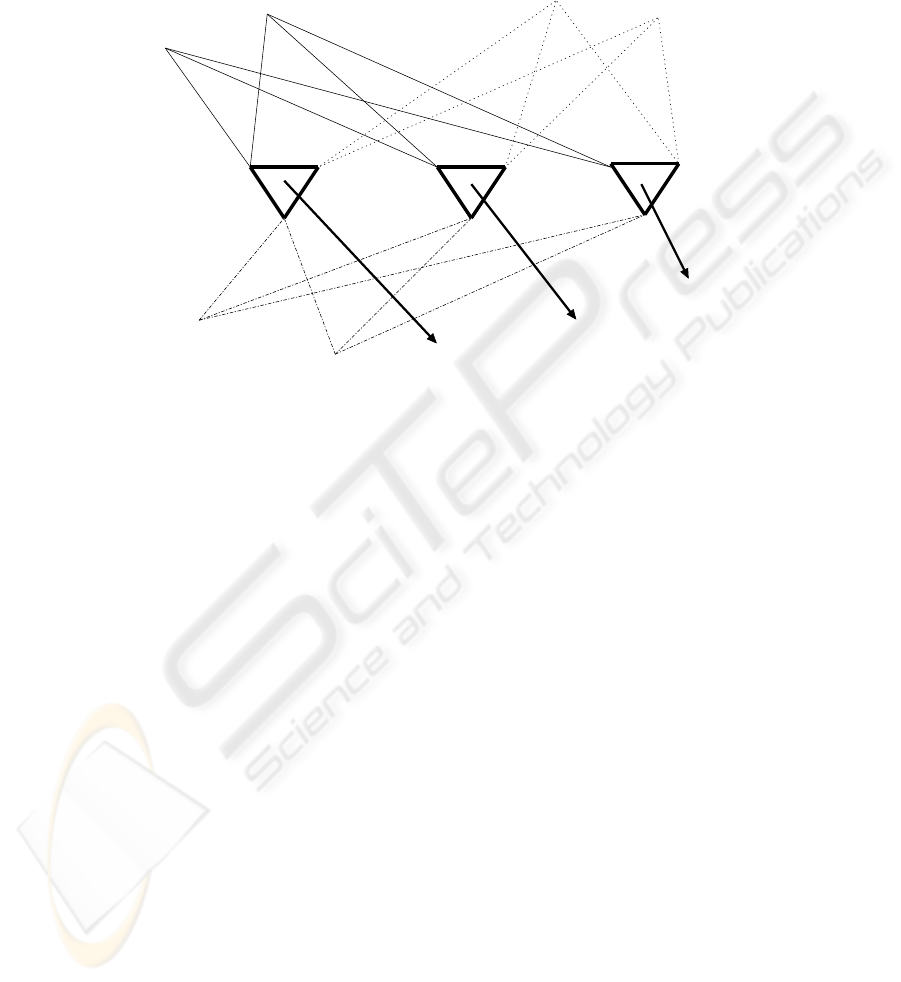
triangles. The number of inputs to the different zones is not necessarily the same, but it
can be made the same by adding zero-weight input signals.
neuron(2)
neuron(3)
output(1)
output(2)
output(3)
neuron(1)
input
1,2
input
2,1
input
2,2
input
1,1
input
3,2
input
3,1
Fig.2. A simple one-layer feedforward network with three CCNs and three input sources is
shown. Each CCN has three receptor zones represented by the vertices of the triangles.
3 How a CCN Network Works
In order to understand the function of the network explained above, consider a one
layer feed-forward network of CCN with N CCNs where each CCN n ∈ N has 3
zones. Assume the centers of the frequency bands B(n, r
1
, t), B(n, r
2
, t), B(n, r
3
, t)
of zones 1, 2 and 3 of CCN n are set to 0.150, 0.450, and 0.750 respectively. Let
the tolerance level T for all zones be 0.050. The range of frequencies for each zone
becomes [B − T, B + T ], i.e, [0.100, 0.200], [0.400, 0.500] and [0.700, 0.800] and let
the thresholds of zones 1, 2, and 3 be τ
1
= 0.20, τ
2
= 0.15, τ
3
= 0.15 respectively and
the CCN body threshold v = 0.32.
Assume that we want the network to store and recall vectors consisting of name,
gender and id of students. Let the input vector be (“Sarah”, “Female”, “4781234”)
which is represented by frequencies (0.130, 0.416, 0.725). Let 0.20 be the amplitude
of each of the components of the vector. As the input vector (assuming first component
of the input vector to zone 1, second component to zone 2 and so on) is applied to
the network, all the zones become active and the CCN starts firing since 0.20 + 0.20 +
0.15 > 0.32. If it does not fire then the tolerance level of inactive zones can be increased
gradually to accommodate the frequency (anti Hebbian learning [5]). Now as the CCN
fires the threshold to each zone is reduced to some minimum level (to some minimum
51

value required to activate the corresponding zone) and the threshold to the cell body
is also reduced to some minimum value. Let the cell body threshold be reduced to
v = 0.18. Now the center of the frequency band of each zone will be assigned the
frequency of its winning signal, i.e., frequencies (0.130, 0.416, and 0.725) are assigned
to zones 1, 2, and 3, respectively and the output vector becomes (0.130, 0.416, 0.725).
Now in the recall phase if we apply only input “Sarah” to zone 1 and no in-
put from the other zones, the CCN will fire (because the threshold 0.20 of signal
“Sarah” is greater than the CCN threshold 0.18) and produce the whole output vec-
tor (0.130, 0.416, 0.725) representing the vector (“Sarah”, “F emale”, “4781234”).
Therefore, if there are R (R-dimensional vector) zones in a CCN, then a single input
signal to a zone will result in R recalled features (R − 1, if we exclude the activating in-
put) from the other zones, which is more efficient than recalling only one feature from
every input compared with the correlation matrix memory. In general, if there are N
CCNs each with R zones (i.e, a CCN can store and recall a R− dimensional vector)
in a one-layer feed forward CCN network then it is able to recall total NR memories.
This is because, after the training is complete a signal (as given in the previous exam-
ple, only input component “Sarah”) to a zone in a CCN will be strong enough to fire
the CCN and recall all the other signals (components) of other zones of that CCN. As
a whole, only N input signals to N CCNs will suffice to recall N R memories. On the
other hand, the correlation matrix memory needs NR CCNs to recall NR memories.
Therefore the achievement of performance in terms of stored-features/number-of-CCNs
ratio is higher in CCN network as compared to correlation matrix memory [3].
4 Limitations in CCN
First, we show that there are certain instances where existing CCN model [1] fails to
produce the expected output result. Then we offer an improvement to the architecture
of the network model such that stipulated performance can be ensured. The associative
network consisting of the proposed CCNs functions well if only one input vector can be
attracted to at most one CCN of the network during training. This is only possible when
no two CCNs have all the centers of the frequency bands (B(n, r, t)) are equal. The net-
work may suffer serious limitation in manipulating (storing and recalling) data when all
the centers of the frequency bands of a CCN coincide with any other CCN. Mathemat-
ically this situation can be expressed as that if there are R zones of a CCN then there
exist at least two CCNs n
i
and n
j
such that B(n
i
, r
1
, t) = B(n
j
, r
1
, t), B(n
i
, r
2
, t) =
B(n
j
, r
2
, t), · · · , B(n
i
, r
R
, t) = B(n
j
, r
R
, t).
Under this circumstances, the network reaches a situation where the same input
vector, M
j
is stored in different CCNs. This is because the input, M
j
stimulates and
fires all those CCNs which have the same centers of frequency bands of their zones.
Here we show how storage capacity decreases for the case stated above. In general,
if the associative memory network has N CCNs and each CCN has R zones we can
store and recall N memory vectors (total NR memories) where each memory vector
M
i
consists of R-components (features). In this way, we can say this is equivalent to
recall exactly NR memories in total. Let S be the number of CCNs that have the same
52

centers of frequency bands of in their zones. This means that there is a memory vector
M
s
whose input can simultaneously fire S CCNs.
As M
s
is stored in all the S CCNs, their centers of frequency bands will be as-
signed the corresponding frequencies of M
s
(each component of M
s
is represented by
a frequency) and no other vector M
t
, (M
s
6= M
t
) can be stored in any of the S CCNs.
So we have only N − S CCNs left to store N − 1 vectors. If S > 1, then we can not
store all the remaining vectors (remaining N −1 vectors, since only one memory vector
M
s
is stored) to the memory. Therefore, this case does not allow us to store and recall
N vectors. In the worst case, if all the N CCNs have the same centers of frequency
bands then we can store only one vector in the whole network instead of N vectors.
Thus the performance degrades down to 1/N percent which is quite worst for large
values of N. In general, if S
1
is the number of CCNs having the same centers of fre-
quency band f
1
1
, · · · , f
1
R
, S
2
is the number of CCNs with the same centers of frequency
band f
2
1
· · · f
2
R
and S
p
is the number of CCNs with the same centers of frequency band
f
p
1
, · · · , f
p
R
then we can achieve p/N percent of vectors to be stored and recalled cor-
rectly where S
1
+ S
2
+ · · · + S
p
= N. The following example demonstrates such a
case.
Suppose the network is required to store input vectors {0, 1, 0, 0}, {1, 1, 0, 0}, {1, 0,
1, 0} and recall when any of the vectors is presented to the network. Assume we have a
network consisting of three CCNs each with four zones. Let the first, second and third
CCN’s band centers are 0.1, 0.2, 0.1, 0.1; 0.1, 0.2, 0.1, 0.1 and 0.2, 0.2, 0.1, 0.1, respec-
tively. Let 0 and 1 be encoded by the frequencies 0.1 and 0.2 respectively. Therefore,
we obtain the equivalent representation of the four input vectors as {0.1, 0.2, 0.1, 0.1},
{0.2, 0.2, 0.1, 0.1} and {0.2, 0.1, 0.2, 0.1}, respectively. As weapply the input {0.1, 0.2,
0.1, 0.1} to activate some CCN, we find all the zones of CCNs 1 and 2 become active
and they (both CCNs) fire. Thus, the input vector {0, 1, 0, 0} is stored in both of them. In
this way, the two CCNs are stimulated and their centers of frequency bands are assigned
the frequencies 0.1, 0.2, 0.1, 0.1. When the second input pattern {0.2, 0.2, 0.1, 0.1} is
presented it stimulates the third CCN and causes it to fire by storing the input frequen-
cies to the corresponding centers of frequency bands. Now for the last input there is no
CCN that can be activated since all the CCNs are already attracted to the two previous
input vectors. Although we have three CCNs to store and recall three vectors according
to the algorithm presented in the paper [1], we cannot store more than two input pat-
terns in the associative memory for this particular example. Thus the performance of
the proposed technique degrades in this case.
5 Solution Proposed for CCNs
In this section, we outline the improvement in the architecture of the CCN neural net-
work to remedy the situation illustrated above. This is intended so that at most one CCN
can be stimulated (attracted) by a single input pattern. The modified network is shown
in Fig. 3.
The main idea is to connect every CCN to all other CCNs and assign indices to them.
These indices, beginning from 1 to the number of CCNs, will be assigned arbitrarily
among the CCNs. It is assumed that the CCN with the lowest index has the highest
53

neuron(1)
neuron(2)
neuron(n)
output(1)
output(2)
output(3)
interconnected CCNs
input
1,1
input
1,2
input
2,1
input
2,2
input
3,1
input
3,2
Fig.3. An improved simple one-layer feedforward network with three CCNs and three input
sources is shown. CCNs are connected to each.
priority and priority will decrease with the increase of indices. After an input pattern is
applied to the network, if a CCN gets stimulated (call it active) then it sends its index
to all other CCNs. If it is not active then it refrains from sending its index. We ensure
that the highest priority active CCN will be the one to be attracted to the input if there
are more than one such active CCNs.
As each active CCN sends its index to all other, every active CCN compares the
index it receives from other active CCNs and if any of the indices is smaller than its
own index then it does not update its center of frequency band. This means that although
it is a candidate for the input to store, it withdraws its candidacy and let other higher
priority CCNs to be attracted to the input. In this way, only the smallest indexed CCN
wins and processes the input and changes its centers of frequency bands of its zones
to the corresponding winning frequencies. In general, we define a one-to-one function
f : S → N , where S denotes the set of CCNs in the network. Let S ⊆ S denote the set
of CCNs simultaneously attracted to a input. It is obvious that there will be exactly one
C
′
∈ S where f(C
′
) 6= f(C
′′
) (C
′′
∈ S − {C
′
}). By following the above procedure
to exchange the indices among the CCNs, we can obtain exactly one active C
′
which
has the smallest index among the indices of the CCNs in S since f is one-to-one. For
example, in a network of 11 CCNs, if CCNs with indices 2, 7, 11 become active for
some input pattern, then the CCNs 7 and 11 will withdraw because they find the index
2 is smaller. As a result, CCN 2 will take over and become stimulated and attracted to
the input. The introduction of priority ensures that at any time when an input pattern
is presented in the network at most one CCN will be attracted to that input. Thus we
eliminate the chance of firing more than one CCNs by a single input which overcomes
the problem mentioned in earlier section.
54

6 Conclusion
Motivated by the resemblance of a pyramidal cell [6] found in brain, the authors of
[1] proposed a new type of model neuron (called CCN) to imitate the behavior of a
pyramidal cell. The pyramidal cell is believed [2] to process both the frequency and
the amplitude of the input signals and there is some sort of competition among inputs.
Attempts are made to follow the physical structure and functional behavior of the pyra-
midal cell to some extent in the CCN, such as competition among the inputs and finally
select the winner. In this paper, we provide an improvement to the CCN model [1]
which is more generalized and can handle situation where there is a chance of getting
activated more than one CCN. Furthermore, we can also increase the memory with our
proposed modification to the architecture of the CCN. Thus the modified neuron model
can increase the memory capacity substantially as demonstrated in this paper.
References
1. Haim Bar, W.L. Miranker, and Alexander Ambash: Competition and Cooperation in Neural
processing. IEEE Transactions on Neural Networkks Vol 53, No 3, March 2004
2. L.C. Rutherford, S.B. Nelson, and G.G Turrigiano; BDNF has opposite effects on the
quantal amplitude of pymidal neuron and interneuron exciatory synapses. Neuron, Vol 21,
pp521-530, September, 1998.
3. http://www.wikipedia.org/
4. J. Singh: Great Ideas in Information Theory, Language and Cybernatics. Newyork, Dover,
1966
5. D.O Hebb: The Organization of Behavior: A Neuropsychological Theory. Newyork, Wiley,
1949
6. M. A. Arbib: The Metaphoricalbrain. Newyork: Wiley-Interscience 1972
7. S. Haykin: Neural Networks, a Comprehensive Foundation. Upper Saddle River, NJ:
Prentice-Hall, 1999
55
