
IMPROVEMENT OF THE VISUAL SERVOING
TASK WITH A NEW TRAJECTORY PREDICTOR
The Fuzzy Kalman Filter
C. P
´
erez, N. Garc
´
ıa, J. M. Sabater, J. M. Azor
´
ın and O. Reinoso
Miguel Hern
´
andez University, Avda. de la Universidad S/N, Elche, Spain
L. Gracia
Technical University of Valencia, Camino Vera S/N, Valencia, Spain
Keywords:
Visual servoing, fuzzy systems, vision / image processing, Kalman filter.
Abstract:
Visual Servoing is an important issue in robotic vision but one of the main problems is to cope with the
delay introduced by acquisition and image processing. This delay is the reason for the limited velocity and
acceleration of tracking systems. The use of predictive techniques is one of the solutions to solve this problem.
In this paper, we present a Fuzzy predictor. This predictor decreases the tracking error compared with the
classic Kalman filter (KF) for abrupt changes of direction and can be used for an unknown object’s dynamics.
The Fuzzy predictor proposed in this work is based on several cases of the Kalman filtering, therefore, we have
named it: Fuzzy Kalman Filter (FKF). The robustness and feasibility of the proposed algorithm is validated
by a great number of experiments and is compared with other robust methods.
1 INTRODUCTION
During the last few years, the use of visual servoing
and visual tracking has been more and more common
due to the increasing power of algorithms and com-
puters.
Visual servoing and visual tracking are techniques
that can be used to control a mechanism according to
visual information. This visual information is avail-
able with a time delay, therefore, the use of predictive
algorithms are widely extended (notice that prediction
of the object’s motion can be used for smooth move-
ments without discontinuities).
The Kalman filter (Kalman, 1960) has become a
standard method to provide predictions and solve the
delay problems (considered the predominant problem
of visual servoing) in visual based control systems
(Corke, 1998), (Dickmanns and V., 1988) and (Wil-
son and Bell, 1996).
The time delay is one of the bigger problems in
this type of systems. For practically all processing ar-
chitectures, the vision system requires a minimum de-
lay of two cycles, but for on-the-fly processing, only
one cycle of the control loop is needed (Chroust and
Vincze, 2003).
Authors of (Chroust and Vincze, 2001) demon-
strate that steady-state Kalman filters (αβ and αβγ
filters) performs better than the KF in the presence
of abrupt changes in the trajectory, but not as good
as the KF for smooth movements. Some research
works about the motion estimation are presented in
(S. Soatto and Perona, 1997) and (Z. Duric and Rivlin,
1996). Further, some motion understanding and tra-
jectory planning based on the Frenet-Serret formula
are described in (J. Angeles and Lopez-Cajun, 1988),
(Z. Duric and Rosenfeld, 1998) and (Z. Duric and
Davis, 1993). Using the knowledge of the motion
and the structure, identification of the target dynamics
may be accomplished.
To solve delay problems, taking into account these
considerations, we propose a new prediction algo-
rithm, the fuzzy Kalman filter (FKF). This filter min-
imizes the tracking error and works better than the
classic KF because it decides what of the used filters
(αβ
slow
/αβ
fast
(Chroust and Vincze, 2003), αβγ, Kv,
Ka and Kj) must be employed. The transition between
them is smooth avoiding discontinuities.
These five filters should be used in a combination
because: The Kalman filter is considered one of the
reference algorithms for position prediction (but we
must consider the right model depending on the ob-
ject’s dynamics: velocity−acceleration−jerk). When
133
Pérez C., García N., M. Sabater J., M. Azorín J., Reinoso O. and Gracia L. (2007).
IMPROVEMENT OF THE VISUAL SERVOING TASK WITH A NEW TRAJECTORY PREDICTOR - The Fuzzy Kalman Filter.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 133-140
DOI: 10.5220/0001643201330140
Copyright
c
SciTePress

the object is outside the image plane, the best predic-
tion is given by steady-state filters (αβ/αβγ depend-
ing on the object’s dynamics: velocity−acceleration).
Obviously, considering more filters and more be-
haviour cases, FKF can be improved but computa-
tional cost of additional considerations can be a prob-
lem in real-time execution. These five filters are con-
sidered by authors as the best consideration (solu-
tion taking into account the prediction quality and the
computational cost). This is the reason to combine
these five filters to obtain the FKF.
This paper is focused on the new FKF filter and
is structured as follows: in section 2 we present the
considered dynamics, the considered dynamics is a
Jerk model with adaptable parameters obtained by
KFs (Nomura and T., 2000), (Li and Jilkov, 2000)
and (Mehrotra and Mahapatra, 1997). In section 3,
we present the block diagram for the visual servo-
ing task. This block diagram is widely used in sev-
eral works like (Corke, 1998) or (Chroust and Vincze,
2003). Section 4 presents the basic idea applied in our
case (see (Wang, 1997b) and (Wang, 1997a)), but the
main work done is focused in one of the blocks de-
scribed in section 3, the Fuzzy Kalman Filter (FKF)
is described in section 5.
In section 6, we can see the results with simulated
data. These results show that FKF can be used to im-
prove the high speed visual servoing tasks. This sec-
tion is organized in two parts: in the first one (Sub-
section 6.1), the analysis of the FKF behaviour is fo-
cussed and in the second one (Subsection 6.2) their
results are compared those with achieved by Chroust
and Vince (Chroust and Vincze, 2003) and with CPA
(Tenne and Singh, 2002) algorithm (algorithm used
for aeronautic/aerospace applications). Conclusions
and future work are presented in section 7.
2 THE DYNAMICS OF A MOVING
OBJECT
The object’s movement is not known (a priori) in
a general visual servoing scheme. Therefore, it is
treated as an stochastic disturbance justifying the use
of a KF as a stochastic observer. The KF algorithm
presented by Kalman (Kalman, 1960) starts with the
system description given by 1 and 2.
x
k+1
= F · x
k
+ G· ξ
k
(1)
y
k
= C· x
k
+ N · η
k
(2)
where x
k
∈ ℜ
nx1
is the state vector and y
k
∈ ℜ
mx1
is
the output vector. The matrix F ∈ ℜ
nxm
is the so-
called system matrix witch describes the propagation
of the state from k to k + 1 and C ∈ ℜ
mxn
describes
the way in which the measurement is generated out of
the state x
k
. In our case of visual servoing m is 1 (be-
cause only the position is measured) and n = 4. The
matrix G ∈ ℜ
nx1
distributes the system noise ξ
k
to the
states and η
k
is the measurement noise. In the KF the
noise sequences η
k
and ξ
k
are assumed to be gaussian,
white and uncorrelated. The covariance matrices of
ξ
k
and η
k
are Q and R respectively (these expressions
consider 1D movement). A basic explanation for the
assumed gaussian white noise sequences is given in
(Maybeck, 1982).
In the general case of tracking, the usual model
considered is a constant acceleration model (Chroust
and Vincze, 2003), but in our case, we consider a con-
stant jerk model described by matrices F and C are:
F =
1 T T
2
/2 T
3
/6
0 1 T T
2
/2
0 0 1 T
0 0 0 1
;C =
1 0 0 0
where T is the sampling time. This model is called a
constant jerk model because it assumes that the jerk
(dx
3
(t)/dt
3
) is constant between two sampling in-
stants.
F and C matrices are obtained from expression 3 to 7:
a− a
i
t − t
i
=
∆a
∆t
= J
0
(3)
x(t) = x
i
+ v
i
(t − t
i
) +
1
2
a
i
(t − t
i
)
2
+
1
6
J
i
(t − t
i
)
3
(4)
v(t) = v
i
+ a
i
(t − t
i
) +
1
2
J
0
(t − t
i
)
2
(5)
a(t) = a
i
+ J
0
(t − t
i
) (6)
J(t) = J
0
(7)
where, x is the position, v is the velocity, a is the ac-
celeration and J is the jerk. So the relation between
them is:
x(t) = f(t); ˙x(t) = v(t); ¨x(t) = a(t);
...
x
(t) = J(t)
3 DESCRIPTION OF THE
CONTROL SYSTEM
The main objective of the visual servoing is to bring
the target to a position of the image plane and to keep
it there for any object’s movement. In figure 1 we
can see the visual control loop presented by Corke in
(Corke, 1998). The block diagram can be used for a
moving camera and for a fixed camera controlling the
motion of a robot. Corke use a KF to incorporate a
feed-forward structure. We incorporate the FKF algo-
rithm in the same structure (see figure 2) but reorder-
ing the blocks for an easier comprehension.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
134
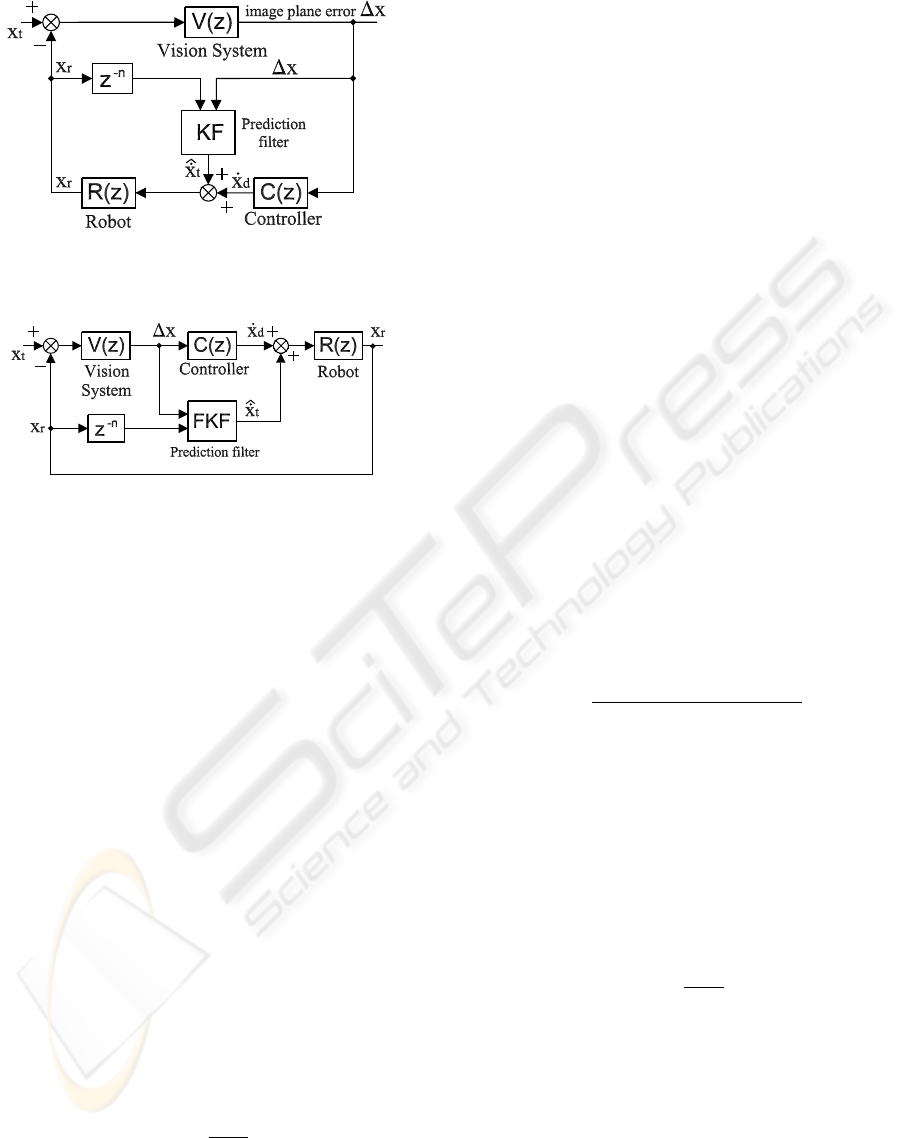
Figure 1: Operation diagram using KF presented by Corke.
Figure 2: Operation diagram using FKF.
V(z) in figure 2 represents the camera behaviour,
which is modeled as a simple delay: V(z) = k
v
· z
−2
(see (Corke, 1998), (Hutchinson and Corke, 1996),
(Vincze and Hager, 2000), (Vincze and Weiman,
1997) and (Vincze, 2000)). C(z) is the controller (A
simple proportional controller is implemented in ex-
periments presented in this paper). R(z) is the robot
(for this work: R(z) = z/z − 1) and the Prediction
filter generates the feedforward signal by prediction
the position of the target. The variable for been mini-
mized is ∆x (generated by the vision system) that rep-
resents the deviation of the target respect to the de-
sired position (error). The controller calculates a ve-
locity signal ˙x
d
which moves the robot in the right di-
rection to decrease the error. Using this approach, no
path planning is needed (the elimination of this path
planning is important because it decreases the com-
putational load (Corke, 1998)).
The transfer function of the robot describes the be-
haviour from the velocity input to the position reached
by the camera, which includes a transformation in the
image plane. Therefore, the transfer function consid-
ered is (Chroust and Vincze, 2003):
R(z) =
z
z− 1
The FKF block is explained in the next sections (sec-
tions 4 and 5).
4 THEORETICAL BACKGROUND
OF THE FUZZY KALMAN
FILTER (FKF)
The most common fuzzy inference process used is
known as Mamdani’s fuzzy inference method, but on
the other hand, we can find a so-called Sugeno, or
Takagi-Sugeno-Kang, method of fuzzy inference. It
was introduced in 1985 (Sugeno, 1985) and is simi-
lar to the Mamdani’s method in many respects. The
first two parts of the fuzzy inference process, fuzzi-
fying the inputs and applying the fuzzy operator, are
exactly the same. The main difference between Mam-
dani and Sugeno is that the Sugeno output member-
ship functions are either linear or constant (for more
information see (Passino and S., 1988)).
For Sugeno regulators, we have a linear dynamic sys-
tem as the output function so that the i
th
rule has the
form:
If ˜z
1
is
˜
A
j
1
and ˜z
2
is
˜
A
k
2
and, ..., and ˜z
p
is
˜
A
l
p
Then
˙x
i
(t) = U
i
x(t) +V
i
u(t)
where x(t) = [x
1
(t),x
2
(t),...,x
n
(t)]
T
is the state
vector, u(t) = [u
1
(t),u
2
(t),...,u
m
(t)]
T
, U
i
and V
i
are the state and input matrices and z(t) =
[z
1
(t),z
2
(t),...,z
p
(t)]
T
is the input to the fuzzy sys-
tem, so:
˙
x(t) =
R
∑
i=1
(U
i
x(t) +V
i
u(t))µ(z(t))
R
∑
i=1
(µ(z(t))
or
˙
x(t) =
R
∑
i=1
(U
i
ξ
i
(z(t))
!
x(t) +
R
∑
i=1
(V
i
ξ
i
(z(t))
!
u(t)
where
ξ
T
= [ξ
1
,...,ξ
R
] =
1
R
∑
i=1
µ
i
[µ
1
,...,µ
R
]
Our work is based on this idea and these expressions
(see (Passino and S., 1988) for more details). We have
mixed the Mamdani’s and the Sugenos’s idea because
we have implemented an algorithm similar to Sugeno
but not for linear systems. We obtain a normalized
weighting of several non linear recursive expressions.
The system works like we can see in figure 3 (see sec-
tion 5).
IMPROVEMENT OF THE VISUAL SERVOING TASK WITH A NEW TRAJECTORY PREDICTOR - The Fuzzy
Kalman Filter
135

Figure 3: Fuzzy Kalman Filter proposed − FKF.
5 THE FUZZY KALMAN FILTER
(FKF)
We have developed a new filter that mixes different
types of Kalman filters depending on the conditions
of the object’s movement. The main advantage of this
new algorithm is the non-abrupt change of the filter’s
output.
Consider the nonlinear dynamic system
˙x = f
1
(x,u); y = g
1
(x,u)
as each one of the filters used. The application of the
fuzzy regulator in our case produces the next space-
state expression:
N
∑
i=1
f
i
(x,u) · ω(x,u)
where
ω(x,u) =
µ
i
(x,u)
N
∑
i=1
µ
j
(x,u)
The final system obtained has the same structure than
filters used:
˙x = f
2
(x,u); y = g
2
(x,u)
Figure 3 shows the FKF block diagram. In this fig-
ure, we can see that the general input is the position
sequence of the target (x
k
). Using this information, we
estimate the velocity, acceleration and jerk of the tar-
get in three separate KFs (Nomura and Naito present
the advantages of this hybrid technique in (Nomura
and T., 2000)). This information is used as ’Input MF’
to obtain F
1
(Ins), F
2
(v), F
3
(a) and F
4
(j). These MF
inputs are the fuzzy membership functions defined in
figure 4. The biggest KF block (rounded) shown in his
figure is a combination of all used algorithms in the
fuzzy filter (αβ
slow
and αβ
fast
(Chroust and Vincze,
2003), αβγ, Kv, Ka and Kj). This block obtains the
output of all specified filters. The ’Output MF’ calcu-
lates the final output using the R
i
rules.
Now, we present the rules (R
i
) considered for the
fuzzy filter:
R
1
: IF object IS inside AND velocity IS low AND
acceleration IS low AND jerk IS low THEN FKF=Kv
R
2
: IF object IS inside AND velocity IS medium
AND acceleration IS low AND jerk IS low THEN
FKF=Kv
R
3
: IF object IS outside AND velocity IS low
AND acceleration IS low AND jerk IS low THEN
FKF=αβ
slow
R
4
: IF object IS outside AND velocity IS medium
AND acceleration IS low AND jerk IS low THEN
FKF=αβ
fast
R
5
: IF object IS inside AND velocity IS high AND
acceleration IS low AND jerk IS low THEN FKF=Kv
R
6
: IF object IS inside AND acceleration IS medium
AND jerk IS low THEN FKF=0.2· αβγ+ 0.8· Ka
R
7
: IF object IS outside AND acceleration IS medium
AND jerk IS low
THEN FKF=0.8· αβγ + 0.2· Ka
R
8
: IF object IS inside AND acceleration IS high
AND jerk IS low
THEN FKF=Ka
R
9
: IF object IS outside AND acceleration IS high
AND jerk IS low
THEN FKF=αβγ
R
10
: IF jerk IS high THEN FKF=K j
These rules have been obtained empirically, based
on the authors experience using the Kalman filter in
different applications.
Notice that rule R
10
(when jerk is high) shows that
the best filter considered is K j and it does not de-
pend on the object’s position (inside or outside) ve-
locity/acceleration value (low, medium or high).
We have used a product inference engine, singleton
fuzzifier and centre average defuzzifier. Figure 4
presents the fuzzy sets definition where (u
max
,v
max
) is
the image size, µ
vel
= µ
acc
= 2m/s, σ
vel
= σ
acc
= 0.5,
c
vel
= c
acc
= 1, d
vel
= d
acc
= 3, i
vel
= i
acc
= 1 and
j
vel
= j
acc
= 1 (these values have been empirically
obtained).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
136
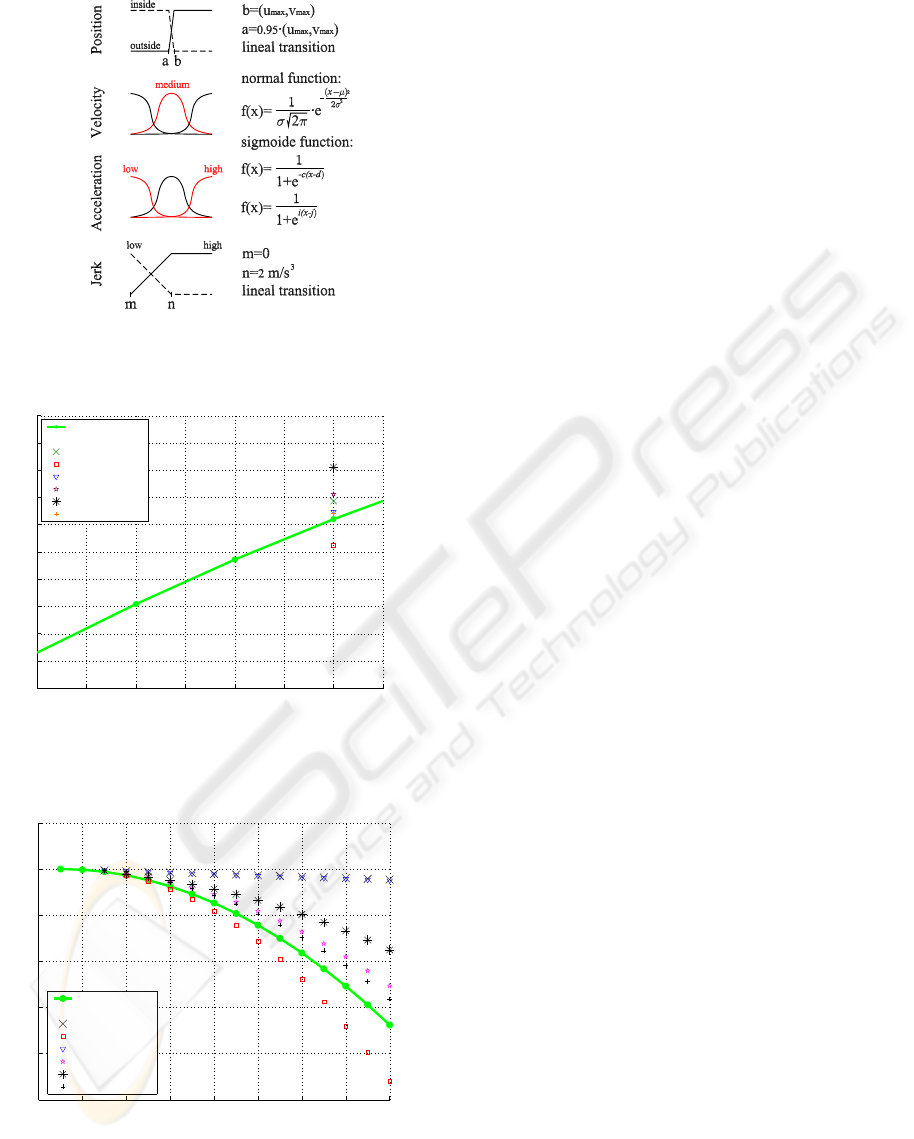
Figure 4: Parameter definition of the fuzzy system.
18 18.5 19 19.5 20 20.5 21 21.5
0
2
4
6
8
10
12
14
16
18
20
Position (pixels)
t (miliseconds)
Real Position
Prediction Ab
Prediction Abg
Prediction Kv
Prediction Ka
Prediction Kj
Prediction FKF
P
k+1
3
P
k+1
6
P
k+1
5
P
k+1
2
P
k+1
4
P
k+1
7
P
k+1
r
P
k
r
P
k−1
r
P
k−2
r
∼
∼
∼
∼
∼
∼
Figure 5: Real position vs. prediction.
0 2 4 6 8 10 12 14 16
−10
0
10
20
30
40
50
Position (pixels)
t (miliseconds)
Real Position
Prediction Ab
Prediction Abg
Prediction Kv
Prediction Ka
Prediction Kj
Prediction FKF
Figure 6: Prediction of a smooth trajectory.
6 RESULTS
This section is composed by two different parts: first
(section 6.1), we analyze the prediction algorithm pre-
sented originally in this paper (FKF block diagram
shown in figure 3) and second (section 6.2), some
simulations of the visual servoing scheme (see figure
2) are done including the FKF algorithm.
6.1 Fuzzy Kalman Filter (FKF) Results
In figure 5, we show the effectiveness of our algo-
rithm’s prediction compared with the classical KF
methods. In this figure, we can see positions P
r
k
(ac-
tual object position), P
r
k−1
(object position in k − 1)
and P
r
k−2
(object position in k− 2). Next real position
of the object will be P
r
k+1
, and points from
e
P
1
k+1
to
e
P
6
k+1
, represent the prediction obtained by each single
filter. The best prediction is given by the FKF filter.
This experiment is done for a parabolic trajectory of
an object affected by the gravity acceleration. (See
figures 5 and 6).
We have done a lot of experiments for different
movements of the object and we have concluded that
our FKF algorithm works better than the others filters
compared (filters compared are: αβ, αβγ, Kv, Ka, Kj
and CPA -see section 6.2- with our FKF). Figure 6
shows the real trajectory and the trajectory predicted
for each filter. For this experiment, we have used the
first four real positions of the object as input for all
filters and they predict the trajectory using only this
information. As we can see in this figure, the best
prediction is again the FKF.
6.2 Visual Servoing Control Scheme
Results
To prove the control scheme presented in figure 2, we
have used the object motion shown in figure 7 (up).
This target motion represents a ramp-like motion be-
tween 1 < t < 4 seconds and a sinusoidal motion for
t > 6 seconds. This motion model is corrupted with
a noise of σ=1 pixel. This motion is used by Stefan
Chroust and Markus Vincze in (Chroust and Vincze,
2003) to analyze the switching Kalman filter (SKF).
For this experiment, we compare the proposed fil-
ter (FKF) with a well known filter, the Circular Pre-
diction Algorithm (CPA) (Tenne and Singh, 2002). In
figure 7 (down), we can see the results of FKF and
CPA algorithms. For changes of motion behaviour,
the FKF produce less error than CPA. For the change
in t=1, the FKF error is [+0.008,-0] and [+0.015,-
0.09] for the CPA. For the change in t=4, FKF error =
IMPROVEMENT OF THE VISUAL SERVOING TASK WITH A NEW TRAJECTORY PREDICTOR - The Fuzzy
Kalman Filter
137
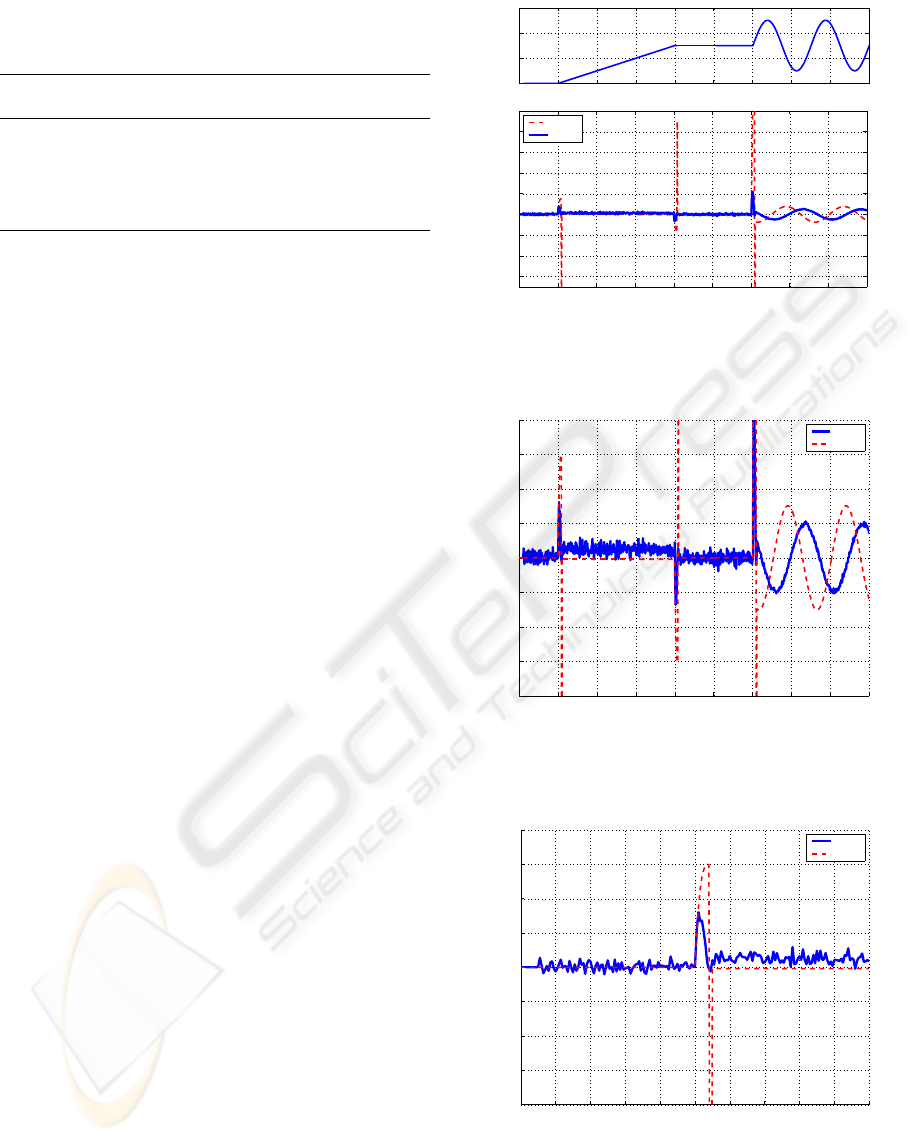
Table 1: Numerical comparative for dispersion value of all
filters implemented (bounce of a ball experiment).
Init. pos. αβ αβγ Kv Ka Kj FKF
40 0.619 0.559 0.410 0.721 0.877 0.353
40(bis) 0.547 0.633 0.426 0.774 0.822 0.340
50 0.588 0.663 0.439 0.809 0.914 0.381
70 0.619 0.650 0.428 0.700 0.821 0.365
90 0.630 0.661 0.458 0.818 0.857 0.343
150 0.646 0.682 0.477 0.848 0.879 0.347
[+0,-0.0072] and CPA error = [+0.09,-0.015]. For the
change in t=6, FKF error = [+0.022,-0] and CPA error
= [+0.122,-0.76]. For the region 6 < t < 9 (sinusoidal
movement between 2.5m and 0.5m) both algorithms
works quite similarly: FKF error = [±0.005] and CPA
error = [±0.0076]. CPA filter works well because it is
designed for movements similar to a sine shape, but
we can compare this results with the SKF filter pro-
posed in (Chroust and Vincze, 2003) and SKF works
better (due to the AKF (Adaptive Kalman Filter) ef-
fect). Therefore, the FKF filter proposed works better
than CPA for all cases analyzed but comparing FKF
with SKF, FKF is better for t=1, t=4 and t=6 but not
for 6 < t < 9 (sinusoidal movement).
Figure 9 shows the zoom region 0 < t < 2 and
−0.02 < ∆x
p
< 0.02 of the same experiment. In this
figure, we can see the fast response of the FKF pro-
posed.
6.3 Experimental Results
Experimental results are obtained for this work us-
ing the following setup: Pulnix GE series high speed
camera (200 frames per second), Intel PRO/1000
PT Server Adapter card, 3.06GHz Intel processor
PC computer, Windows XP Professional O.S. and
OpenCV blob detection library.
For this configuration, the bounce of a ball on the
ground is processed to obtain data shown in figure 10.
Results of this experiment are presented in table 1.
In this table, we can see the dispersion of several fil-
ters. The FKF dispersion is less than αβ, αβγ, Kv,
Ka and Kj although FKF is a combination of them.
This table contains data from this particular experi-
ment (the bounce of a ball on the ground). For this
experiment, the position of the ball is introduced to
the filters to prove the behaviour of them. The filter
proposed (FKF) is the best analyzed.
In figure 11 we can see some frames of the experi-
ment ’bounce of a ball on the ground’. For each frame
the center of gravity of the tennis ball is obtained.
0 1 2 3 4 5 6 7 8 9
0
1
2
3
Target motion (m)
0 1 2 3 4 5 6 7 8 9
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
0.1
∆x
p
(m)
t (seconds)
CPA
FKF
Figure 7: Simulation result for tracking an object.
0 1 2 3 4 5 6 7 8 9
−0.02
−0.015
−0.01
−0.005
0
0.005
0.01
0.015
0.02
∆x
p
(m)
t (seconds)
CPA
FKF
Figure 8: Zoom of the simulation.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−0.02
−0.015
−0.01
−0.005
0
0.005
0.01
0.015
0.02
∆x
p
(m)
t (seconds)
CPA
FKF
Figure 9: Zoom between 0 and 2 seconds.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
138

0 10 20 30 40 50 60 70 80 90 100
−5
0
5
10
15
20
25
30
35
40
Position (pixels)
t (miliseconds)
Real Position
Prediction Ab
Prediction Abg
Prediction Kv
Prediction Ka
Prediction Kj
Prediction FKF
Figure 10: Bounce of the ball on the ground. Data.
Figure 11: Bounce of the ball on the ground. Frames.
7 CONCLUSIONS AND FUTURE
WORK
In section 6.1 (figures 5 and 6), we can see the qual-
ity of the new filter presented (FKF) which shows
good behaviour for smooth and discontinuous mo-
tions. The object’s position is estimated even when
it is inside the image plane and when it is outside the
image plane. Therefore, combine classic filters (KF)
when inside and steady-state filters (αβ/αβγ) when
outside.
We have compared our filter with αβ, αβγ, Kv,
Ka and Kj in experiments of pure prediction. We
have compared too, our filter with Circular Predic-
tion Algorithm (CPA) in this paper reproducing the
same experiment as (Chroust and Vincze, 2003) for a
direct comparison with the work done by Chroust and
Vincze. The filter proposed works very well but not
better than SKF for all conditions, therefore, the addi-
tion of a AKF action can improve the filter behaviour
(future work).
The FKF is evaluated with a ramp-like and
sinosoidal motions. ∆x
p
is reduced in all tests done
and the overshoot is decreased significantly.
Results presented in this paper are obtained forC(z) =
K
P
. Other controllers like PD, PID, ... will be imple-
mented in future work.
ACKNOWLEDGEMENTS
This work is supported by the Plan Nacional de
I+D+I 2004-2007, DPI2005-08203-C02-02 of the
Spanish Government (T
´
ecnicas Avanzadas de Tele-
operaci
´
on y Realimentaci
´
on Sensorial Aplicadas a la
Cirug
´
ıa Asistida por Robots).
REFERENCES
Chroust, S. and Vincze, M. (2003). Improvement of the
prediction quality for visual servoing with a switching
kalman filter. I. J. Robotic Res., 22(10-11):905–922.
Chroust, S., Z. E. and Vincze, M. (2001). Pros and cons of
control methods of visual servoing. In In Proceedings
of the 10th International Workshop on Robotics in the
Alpe-Adria-Danube Region.
Corke, P. I. (1998). Visual Control of Robots: High Per-
formance Visual Visual Servoing. Research Studies
Press, Wiley, New York, 1996 edition.
Dickmanns, E. D. and V., G. (1988). Dynamic monocular
machine vision. In Applications of dinamyc monoclar
machine vision. Machine Vision and Applications.
IMPROVEMENT OF THE VISUAL SERVOING TASK WITH A NEW TRAJECTORY PREDICTOR - The Fuzzy
Kalman Filter
139

Hutchinson, S., H. G. D. and Corke, P. (1996). Visual ser-
voing: a tutorial. In Transactions on Robotics and
Automation. IEEE Computer Society.
J. Angeles, A. R. and Lopez-Cajun, C. S. (1988). Trajectory
planning in robotics continuous-path applications. In
Journal of Robotics and Automation. IEEE Computer
Society.
Kalman, R. E. (1960). A new approach to linear filter-
ing and prediction problems. In IEEE Transactions
on Pattern Analysis and Machine Intelligence. IEEE
Computer Society.
Li, X. and Jilkov, V. (2000). A survey of maneuvering target
tracking: Dynamic models. In Signal and Data Pro-
cessing of Small Targets. The International Society for
Optical Engineering.
Maybeck, P. S. (1982). Stochastic Models, Estimation and
Control. Academic Press, New York.
Mehrotra, K. and Mahapatra, P. R. (1997). A jerk model
for tracking highly maneuvering targets. In Trans-
actions on Aerospace and Electronic Systems. IEEE
Computer Society.
Nomura, H. and T., N. (2000). Integrated vsual servoing
sysem to grasp industrial parts moving on conveyer
by controlling 6dof arm. In Internacional Conference
on Systems, Man. and Cybernetics. IEEE Computer
Society.
Passino, K. M. and S., Y. (1988). Fuzzy Control. Addison-
Wesley, Ohio, USA.
S. Soatto, R. F. and Perona, P. (1997). Motion estimation via
dynamic vision. In IEEE Transactions on Automatic
Control. IEEE Computer Society.
Sugeno, M. (1985). Industrial applications of fuzzy control.
Elsevier Science Publications Company.
Tenne, D. and Singh, T. (2002). Circular prediction
algorithms-hybrid filters. In American Control Con-
ference. IEEE Computer Society.
Vincze, M. (2000). Real-time vision, tracking and control-
dynamics of visual servoing. In International Con-
ference on Robotics and Automation. IEEE Computer
Society.
Vincze, M. and Hager, G. D. (2000). Robust Vision for
Vision-Based Control of Motion. SPIE Press / IEEE
Press, Bellingham, Washington.
Vincze, M. and Weiman, C.(1997). On optimizing window-
size for visual servoing. In International Conference
on Robotics and Automation. IEEE Computer Society.
Wang, L.-X. (1997a). Course In Fuzzy Systems and Control,
A. Prentice Hall.
Wang, L.-X. (1997b). Course in Fuzzy Systems and Con-
trol Theory. Pearson US Imports & PHIPEs. Pearson
Higher Education.
Wilson, W. J., W. H. C. C. and Bell, G. S. R. (1996).
Relative end-effector control using cartesian position
based visual servoing. In IEEE Transactions on
Robotics and Automation. IEEE Computer Society.
Z. Duric, E. R. and Davis, L. (1993). Egomotion analysis
based on the frenet-serret motion model. In Proceed-
ings of the 4th International Conference on Computer
Vision. IEEE Computer Society.
Z. Duric, E. R. and Rosenfeld, A. (1998). Understanding the
motions of tools and vehicles. In Proceedings of the
Sixth International Conference on Computer Vision.
IEEE Computer Society.
Z. Duric, J. A. F. and Rivlin, E. (1996). Function from mo-
tion. In Transactions on Pattern Analysis and Machine
Intelligence. IEEE Computer Society.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
140
