
HEURISTIC ALGORITHMS FOR SCHEDULING IN A
MULTIPROCESSOR TWO-STAGE FLOWSHOP
WITH 0-1 RESOURCE REQUIREMENTS
Ewa Figielska
Warsaw School of Computer Science, Lewartowskiego 17, 00-169 Warsaw, Poland
Keywords: Heuristics, Linear Programming, Flowshop scheduling, Parallel unrelated machines, Resource constraints.
Abstract: This paper deals with the problem of preemptive scheduling in a two-stage flowshop with parallel unrelated
machines at the first stage and a single machine at the second stage. At the first stage, jobs use some
additional resources which are available in limited quantities at any time. The resource requirements are of
0-1 type. The objective is the minimization of makespan. The problem is NP-hard. Heuristic algorithms are
proposed which, while solving to optimality the resource constrained scheduling problem at the first stage
of the flowshop, select for simultaneous processing jobs according to rules promising a good (short)
schedule in the flowshop. Several rules of job selection are considered. The performance of the proposed
heuristic algorithms is analyzed by comparing their solutions with the lower bound on the optimal
makespan. The results of computational experiments show that these heuristics are able to produce near-
optimal solutions in short computation time.
1 INTRODUCTION
During the last years, the flowshops with multiple
processors (FSMP) also called hybrid flowshops,
have received considerable attention from
researchers (e.g. Gupta 1988; Chen 1995; Haouari
and M’Hallah, 1997; Brah and Loo (1999), Linn and
Zhang, 1999; Ruiz and Maroto, 2006).
In this paper, we extend multiprocessor flowshop
scheduling research by including resource
constraints. We consider the problem of scheduling
in a two-stage flowshop where jobs use additional
renewable resources, which are available in limited
quantities at any time. This problem can be
described as follows. There are
n preemptive jobs
to be processed at two stages in the same
technological order, first at stage 1 then at stage 2.
At stage 1 there are
m
parallel unrelated machines,
stage 2 has one machine. A job upon finishing its
processing at stage 1 is ready to be processed at
stage 2; it may be processed at stage 2 when the
machine is available there, or it may reside in a
buffer space of unlimited capacity following stage 1
until the machine at stage 2 becomes available. At
stage 1, a job can be processed on any of the parallel
machines, and its processing times may be different
on different machines. The processing times of job
j ( nj ,,1 …
=
) are equal to
ij
p (if it is executed on
machine
i
( mi ,,1 …
=
)) and
j
s
time units,
respectively, at stage 1 and at stage 2. The
processing of a job on a machine of stage 1 may be
interrupted at any moment and resumed later on the
same or another machine. A job during its
processing at stage 1 does not need a resource or
uses one unit of this resource (0-1 resource
requirements). There are
l types of resources. A
resource of type
r
( lr ,,1 …
=
) is available in an
amount limited to
r
W units at a time. The total usage
of resource
r
at any moment by jobs simultaneously
executed on parallel machines cannot exceed the
availability of this resource. The objective is to find
a feasible schedule which minimizes makespan,
max
C , which is equal to the maximum job
completion time at stage 2.
The considered problem is NP-hard in the strong
sense since the problem of preemptive scheduling in
the two-stage flowshop with two identical parallel
machines at one stage and one machine at another is
NP-hard in the strong sense (Hoogeveen et al.,
1996).
452
Figielska E. (2007).
HEURISTIC ALGORITHMS FOR SCHEDULING IN A MULTIPROCESSOR TWO-STAGE FLOWSHOP WITH 0-1 RESOURCE REQUIREMENTS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 452-455
DOI: 10.5220/0001643404520455
Copyright
c
SciTePress

The heuristic algorithms proposed for the
considered problem, while solving to optimality the
resource constrained scheduling problem at the first
stage of the flowshop, select for simultaneous
processing jobs according to rules promising a good
(short) schedule in the flowshop. Several rules of job
selection are considered.
The problem under consideration arises in real-
life systems that are encountered in a variety of
industries, e.g. in chemical, food, cosmetics and
textile industries. These systems are often subjected
to some additional resource constraints for example
on the availability of the additional resources such as
skilled labour and tools. Preemption of jobs usually
results in shortening the schedule. The problem with
parallel unrelated machines at the first stage and a
single machine at the second stage may arise in a
manufacturing environment in which products are
initially processed on any of parallel machines and
then each product must go through a final testing
operation, which is to be carried out on a common
testing machine.
2 FRAMEWORK OF THE
HEURISTIC ALGORITHMS
The proposed heuristic algorithms proceed in the
following steps:
1. A linear programming (LP) problem is solved to
minimize time
T needed for finishing all jobs
at stage 1 of the flowshop under relaxed
resource constraints over time
T
. As a result,
the minimal value of
T and the values of the
time
ij
t (
njmi ,,1,,,1 …… ==
) during which
job
j
is processed on machine i are obtained.
2. Using the values of
ij
t obtained in Step 1 as
well as the values of
j
s (
j
s is the processing
time of job
j
at stage 2), weights,
j
w
, for all
jobs are determined on the basis of 6 different
expressions presented in Table 1.
3. The schedule at stage 1 of the flowshop is
constructed in the form of a sequence of partial
schedules using the values of
T
,
ij
t , and
j
w .
In a partial schedule at most m (m is the
number of machines) jobs are assigned to
machines for simultaneous processing during
some period of time so that resource constraints
are satisfied at every moment. The consecutive
partial schedules are created in subsequent
iterations of an iterative procedure. Assignment
of jobs to machines in a partial schedule is
found maximizing the weighted assignment
ij
m
i
n
j
j
vw
∑∑
==11
(
ij
v = 1 if job
j
is processed
on machine
i in a current partial schedule, and
0 otherwise) under resource constraints. In each
created partial schedule, conditions on
optimality formulated in (Slowinski, 1980,
1981) are satisfied.
4. Completion times of jobs at stage 1 are
calculated.
5. A schedule on the machine of stage 2 is
constructed using the values of
j
s , and ready
times of jobs at stage 2, which are equal to
corresponding completion times at stage 1.
Table 1: Weights used in the heuristic algorithms.
Algorithm
Weight
j
w of job
j
A1 1
A2
random number from
)1,0[U
A3
{
}
j
knk
Z
Z
,,1
min
…=
A4
{}
knk
j
s
s
,,1
max
…=
A5
{
}
{}
knk
knk
j
j
s
Z
Z
s
,,1
,,1
max
min
…
…
=
=
A6
{
}
j
knk
Z
Z
,,1
min
…=
+1 if
jj
sZ ≤ ,and
{}
knk
j
s
s
,,1
max
…=
if
jj
sZ >
j
Z is the processing time of job
j
at stage 1,
j
Z =
∑
=
m
i
ij
t
1
. In A3, A4 and A5 the maximal value of
j
w is equal to 1, in A6 the maximal
j
w is equal to 2 if
jj
sZ
≤
, and 1 if
jj
sZ > .
3 ILLUSTRATIVE EXAMPLE
To illustrate the problem and the solution method we
present the following example. Consider the case of
the two-stage flowshop with 2 machines at stage 1
and a single machine at stage 2. The number of jobs
n =10, the resource availability at any moment,
1
W =1. Job processing times and resource
requirements are shown in Figure 1.
HEURISTIC ALGORITHMS FOR SCHEDULING IN A MULTIPROCESSOR TWO-STAGE FLOWSHOP WITH 0-1
RESOURCE REQUIREMENTS
453
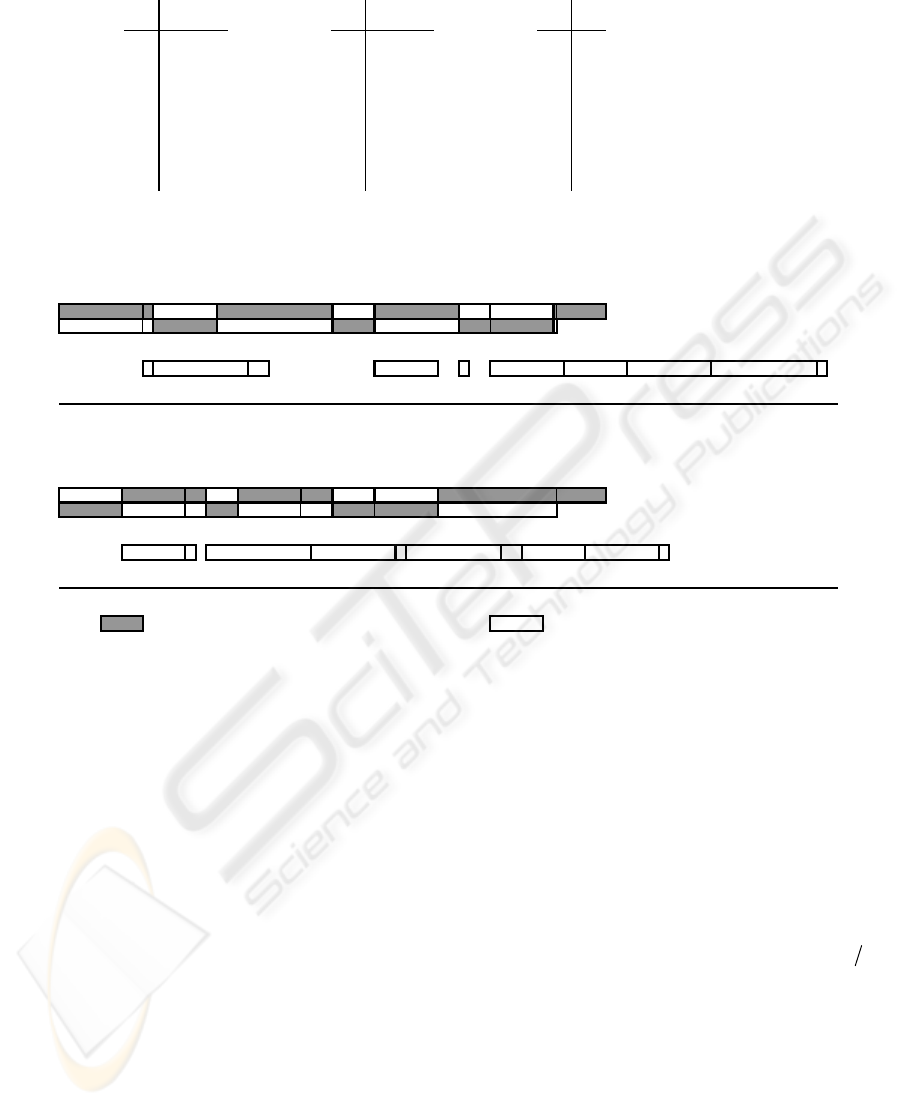
j
ob processing times job processing times resource requirements
at stage 1: at stage 2: at stage 1:
machine machine
j
ob 1 2
j
ob 1
j
ob
1610 1 1 11
resource availability = 1
214 9 2 8 2 1
312 8 3 10 3 0
41310 4 6 4 1
5612 5 6 50
62316 6 7 6 0
768 7 2 70
813 9 8 9 8 0
91922 9 1 9 1
10 8 23 10 1 10 1
Figure 1: Data for an illustrative example.
(a)
partial sch.
index: 1 2 3 4 5 6 7 8 9 10
stage: 1
1m11017 9 6 9651
m2884 64322
3
2m1 87 49652 31
10
time
010203040506070
(b)
partial sch.
index: 1 2 3 4 5 6 7 8 9 10
stage:
1m1 5 1 10 6 10 9 6 7 9 9
m2 2 332 8 84 4 6
2m1 5 1 3 2 8 7 4 6 9
10
time
010203040506070
processing time of a job using a resource at stage 1 processing time of a job which does not use a resourc
e
Figure 2: An illustrative example. The resulting schedules: (a) a schedule obtained by heuristic algorithm A1, (b) a schedule
obtained by heuristic algorithm A5.
Figure 2 presents two flowshop schedules for this
instance, one created by algorithm A1 (Figure 2a)
and another created by A5 (Figure 2b). The first
stage schedules in Figures 2a and 2b are composed
of 10 partial schedules. In each of these partial
schedules at most 2 jobs are processed
simultaneously and the total resource usage does not
exceed the resource availability,
1
1
=W , e.g. in the
partial schedule of index 1 in Figure 2a, jobs 10 and
8 are processed simultaneously and use at every
moment 1 and 0 units of the resource, respectively.
The first stage schedules in Figures 2a and 2b have
the same length, but completion times of jobs in
these schedules are different. For example, in the
first stage schedule in Figure 2a, job 10 finishes its
processing at stage 1 at 8 time units and in Figure 2b
- at 23 time units. This results in different lengths of
the flowshop schedules provided by A1 and A5.
4 COMPUTATIONAL STUDY
In this section, the results of a computational
experiment conducted to evaluate the performance
of the proposed heuristic algorithm are presented.
720 randomly generated instances were created and
examined. Instances were generated for =n 50, 100,
150, and 200,
=
m 2, 4, and 6, and for one resource
type. The resource availability
1
W was set at 2m ,
and for 55% of jobs resource requirements were set
at 1. Processing times at stage 2,
j
s , were generated
from
]100,1[U
(
],[ baU
denotes the discrete
uniform distribution in the range of
],[ ba ) for all
instances. Processing times at stage 1,
ij
p , were
generated from 9 ranges: U[30,120], U[45,180], and
U [60,240] for instances with m = 2, U [90,360], U
[120,480], and U [150,600] for m = 4, U[150,600],
U[200,800], and U [250,1000] for m = 6. The ranges
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
454

for processing times were selected so as to include
the cases when the length of the optimal schedule at
stage 1,
*
1
C , is close to the sum of job processing
times at stage 2,
∑
=
n
j
j
s
1
.
As an effectiveness measure we use the relative
percentage deviation of a heuristic solution from the
lower bound on the optimal makespan defined as
%100
max
×
−
=
LB
LBC
δ
where
},max{
21
LBLBLB = , where
1
LB =
*
1
C +
)(min
,,1 jnj
s
…=
and
2
LB = )(min
,,1,,,1 ijnjmi
p
…… ==
+
∑
=
n
j
j
s
1
,
*
1
C is the minimal makespan at stage 1.
Table 2: Computational results.
δ
(%)
n m
A1 A2 A3 A4 A5 A6
50 2 1.38 1.40 0.06 0.75 0.06 0.04
2.78 3.35 1.30 0.54 0.12 0.06
4.15 4.43 2.74 0.27 0.20 0.14
4 3.26 1.94 0.31 0.46 0.15 0.40
7.21 4.60 3.77 0.60 0.52 0.60
7.68 6.25 5.81 0.82 0.89 0.74
6 2.65 1.39 0.25 0.52 0.16 0.52
8.24 5.16 4.64 0.87 0.77 0.84
8.90 7.80 6.87 1.55 1.68 1.51
100 2 0.74 0.51 0.03 0.39 0.02 0.01
1.80 2.49 0.60 0.21 0.04 0.02
1.52 1.33 1.00 0.03 0.05 0.02
4 1.26 1.08 0.08 0.26 0.08 0.25
5.06 3.18 1.87 0.18 0.22 0.18
3.45 2.70 2.50 0.17 0.21 0.16
6 2.03 1.01 0.06 0.23 0.07 0.25
5.64 4.03 2.46 0.40 0.31 0.42
4.02 4.03 3.76 0.47 0.47 0.43
150 2 0.21 0.42 0.02 0.19 0.02 0.00
1.62 1.16 0.28 0.19 0.02 0.01
0.95 0.90 0.91 0.02 0.02 0.02
4 0.71 0.61 0.00 0.22 0.01 0.16
4.24 2.05 1.44 0.15 0.10 0.19
1.94 1.60 1.37 0.06 0.07 0.06
6 0.76 0.49 0.04 0.20 0.01 0.20
4.14 2.36 1.86 0.24 0.17 0.24
2.66 2.46 2.17 0.18 0.20 0.19
200 2 0.46 0.42 0.01 0.21 0.02 0.00
1.10 0.99 0.17 0.30 0.01 0.01
0.69 0.48 0.38 0.01 0.01 0.01
4 0.60 0.44 0.04 0.19 0.03 0.10
2.15 1.70 0.86 0.12 0.05 0.12
1.47 1.22 1.16 0.05 0.05 0.05
6 0.83 0.25 0.02 0.10 0.03 0.10
2.46 1.57 0.90 0.12 0.07 0.12
1.75 1.67 1.64 0.10 0.10 0.10
The results of a computational experiment are
presented in Table 2 All entries in this table are
average values over 20 instances.
From Table 2, we can observe that deviations,
δ
, significantly decrease, as the number of jobs
grows, and they increase with the number of
machines. We can see that algorithms A3, A4, A5,
and A6 always outperform A1 and A2, and A4, A5,
and A6 produce near-optimal solutions. On the
average over the entire collection of instances,
relative deviations of the heuristic makespan from its
lower bound are equal to 2.79%, 2.15%, 1.43%,
0.32%, 0.19%, and 0.23% for A1, A2, A3, A4, A5,
and A6, respectively.
The CPU times are small for all the heuristic
algorithms and equal to about 0.3, 1.5, 3, 4.5, and
6.5 seconds for n =50, 100, 150, and 200,
respectively.
REFERENCES
Brah, S.A. and L.L. Loo (1999). Heuristics for scheduling
in a flow shop with multiple processors. Europ. J. of
Opernl Res.113,113-112
Chen, B. (1995). Analysis of classes of heuristics for
scheduling a two-stage flow shop with parallel
machines at one stage, J. of Opernl Res. Soc. 46, 234-
244.
Gupta J.N.D. (1988). Two stage hybrid flowshop
scheduling problem. J. of Opernl Res. Soc. 39, 359-
364.
Haouari, M. and R. M’Hallah (1997). Heuristic algorithms
for the two-stage hybrid flowshop problem, Oper. Res.
Let. 21, 43-53.
Hoogeveen J.A., J.K. Lenstra and B. Veltman (1996).
Preemptive scheduling in a two-stage multiprocessor
flow shop is NP-hard. Europ. J. of Opernl Res. 89,
172-175.
Linn, R, W. Zhang (1999). Hybrid flow shop scheduling: a
survey. Comp. and Ind. Engin. 37, 57-61.
Ruiz, R., C. Maroto (2006). A genetic algorithm for hybrid
flowshops with sequence dependent setup times and
machine eligibility. Europ. J. of Opernl Res. 169, 781-
800.
Slowinski, R. (1980), Two approaches to problems of
resource allocation among project acticities – A
comparative study. J. Opl Res. Soc. 31, 711-723.
Slowinski, R. (1981), L'ordonanacement des taches
preemptives sur les processeurs independants en
presence de ressources supplementaires. RAIRO
Inform./Comp. Science, vol.15, No.2, 155-166.
HEURISTIC ALGORITHMS FOR SCHEDULING IN A MULTIPROCESSOR TWO-STAGE FLOWSHOP WITH 0-1
RESOURCE REQUIREMENTS
455
