
ROBOT TCP POSITIONING WITH VISION
Accuracy Estimation of a Robot Visual Control System
Drago Torkar and Gregor Papa
Computer Systems Department, Jožef Stefan Institute, Jamova c. 39, SI-1000 Ljubljana, Slovenia
Keywords: Robot control, Calibrated visual servoing.
Abstract: Calibrated 3D visual servoing has not fully matured as a industrial technology yet, and in order to widen its
use in industrial applications its technological capability must be precisely known. Accuracy and
repeatability are two of the crucial parameters in planning of any robotic task. In this paper we describe a
procedure to evaluate the 2D and 3D accuracy of a robot stereo vision system consisting of two identical 1
Megapixel cameras, and present the results of the evaluation.
1 INTRODUCTION
In the last decades, more and more robots
applications were used in industrial manufacturing
which was accompanied by an increased demand for
versatility, robustness and precision. The demand
was mostly satisfied by increasing the mechanical
capabilities of robot parts. For instance, to meet the
micrometric positioning requirements, stiffness of
the robot’s arms was increased, high precision gears
and low backlash joints introduced, which often led
to difficult design compromises such as the request
to reduce inertia and increase stiffness. This results
in approaching the mechanical limits and increased
cost of robots decreasing the competitiveness of the
robot systems on the market (Arflex, 2005).
Lately, the robot producers have put much effort
into incorporating visual and other sensors to the
actual industrial robots thus providing a significant
improvement in accuracy, flexibility and
adaptability. Vision is still one of the most
promising sensors (Ruf and Horaud, 1999) in real
robotic 3D servoing issues (Hutchinson et al., 1995).
It has been vastly investigated for the last two
decades in laboratories but it's only now that it finds
its way to industrial implementation (Robson, 2006)
in contrast to machine vision which became a well
established industry in the last years (Zuech, 2000).
There are many reasons for this. The vision systems
used with the robots must satisfy a few constraints
that differ them from a machine vision measuring
systems. First of all, the camera working distances
are much larger, especially with larger robots that
can reach several meters. Measuring at such
distances with high precision requires much higher
resolution which very soon reaches its technological
and price limits. For example, nowadays 4
Megapixel cameras are the state of the art in vision
technology but are not affordable in many robotic
applications since their price almost reaches the
robot price. The dynamics of the industrial processes
requires high frame rates which in connection with
real time processing puts another difficult constraint
on system integrators. The unstructured industrial
environment with changing environmental lighting
is another challenge for the robot vision specialists.
When designing the vision system within robot
applications it is very important to choose the
optimal equipment for the task and to get maximal
performance out of each component. In the paper we
represent a procedure for the precision estimation of
a calibrated robot stereo vision system in 2D and 3D
environment. Such a system can be used in visual
servoing applications for precise tool center point
(TCP) positioning.
2 METHODOLOGY
Four types of accuracy tests were performed: a static
2D test, a dynamic 2D test, a static 3D test, and a
dynamic 3D test. Throughout all the tests, an array
of 10 infrared light emitting diodes (IR-LED) was
used to establish its suitability for being used as a
212
Torkar D. and Papa G. (2007).
ROBOT TCP POSITIONING WITH VISION - Accuracy Estimation of a Robot Visual Control System.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 212-215
DOI: 10.5220/0001643502120215
Copyright
c
SciTePress

marker and a calibration pattern in the robot visual
servoing applications.
Within the static 2D test, we were moving the
IR-LED array with the linear drive perpendicular to
the camera optical axes and measured the increments
in the image. The purpose was to detect the smallest
linear response in the image. The IR-LED centroids
were determined in two ways: on binary images and
on grey-level images as centers of mass. During
image grabbing the array did not move thus
eliminating any dynamic effects. We averaged the
movement of centroids of 10 IR-LEDs in a sequence
of 16 images and calculated the standard deviation
to obtain accuracy confidence intervals. With the
dynamic 2D test shape distorsions in the images due
to fast 2D movements of linear drive were
investigated. We compared a few images of IR-LED
array taken during movement to statically obtained
ones which provided information of photocenter
displacements and an estimation of dynamic error.
We performed the 3D accuracy evaluation with 2
fully calibrated cameras in a stereo setup. Using
again the linear drive, the array of IR-LEDs was
moved along the line in 3D space with different
increments and the smallest movement producing a
linear response in reconstructed 3D space was
sought. In the 3D dynamic test, we attached the IR-
LED array to the wrist of an industrial robot, and
dynamically guided it through some predefined
points in space and simultaneously recorded the
trajectory with fully calibrated stereo cameras. We
compared the reconstructed 3D points from images
to the predefined points fed to robot controller.
3 TESTING SETUP
The test environment consisted of:
PhotonFocus MV-D1024-80-CL-8 camera with
CMOS sensor and framerate of 75 fps at full
resolution (1024x1024 pixels),
Active Silicon Phoenix-DIG48 PCI frame
grabber,
Moving object (IR-LED array) at approximate
distance of 2m. The IR-LED array (standard
deviation of IR-LED accuracy is below 0.007
pixel, as stated in (Papa and Torkar, 2006))
fixed to Festo linear guide (DGE-25-550-SP)
with repetition accuracy of +/-0.02mm.
For then static 2D test the distance from camera
to a moving object (in the middle position) that
moves perpendicularly to optical axis was 195cm;
camera field-of-view was 220cm, which gives pixel
size of 2.148mm; Schneider-Kreuznach lens
CINEGON 10mm/1,9F with IR filter; exposure time
was 10.73ms, while frame time was 24.04ms, both
obtained experimentally.
For the dynamic 2D test conditions were the
same as in static test, except the linear guide was
moving the IR-LED array with a speed of 460mm/s
and the exposure time was 1ms.
In the 3D reconstruction test the left camera
distance to IR-LED array and right camera distance
to IR-LED array were about 205cm; baseline
distance was 123cm; Schneider-Kreuznach lens
CINEGON 10mm/1,9F with IR filter; Calibration
region-of-interest (ROI): 342 x 333 pixels;
Calibration pattern: 6 x 8 black/white squares;
Calibration method (Zhang, 1998); Reconstruction
method (Faugeras, 1992). The reconstruction was
done off-line and the stereo correspondence problem
was considered solved due to a simple geometry of
the IR-LED array and is thus not addressed here.
For the 3D dynamic test, an ABB industrial robot
IRB 140 was used with the standalone fully
calibrated stereo vision setup placed about 2m away
from its base and calibrated the same way as before.
The robot wrist was moving through the corners of
an imaginary triangle with side length of
approximately 12cm. The images were taken
dynamically when the TCP was passing the corner
points and reconstructed in 3D with an approximate
speed of 500mm/s. The relative length of such
triangle sides were compared to the sides of a
statically-obtained and reconstructed triangle. The
robot native repeatability is 0.02 mm and its
accuracy is 0.01mm.
4 RESULTS
4.1 2D Accuracy Tests
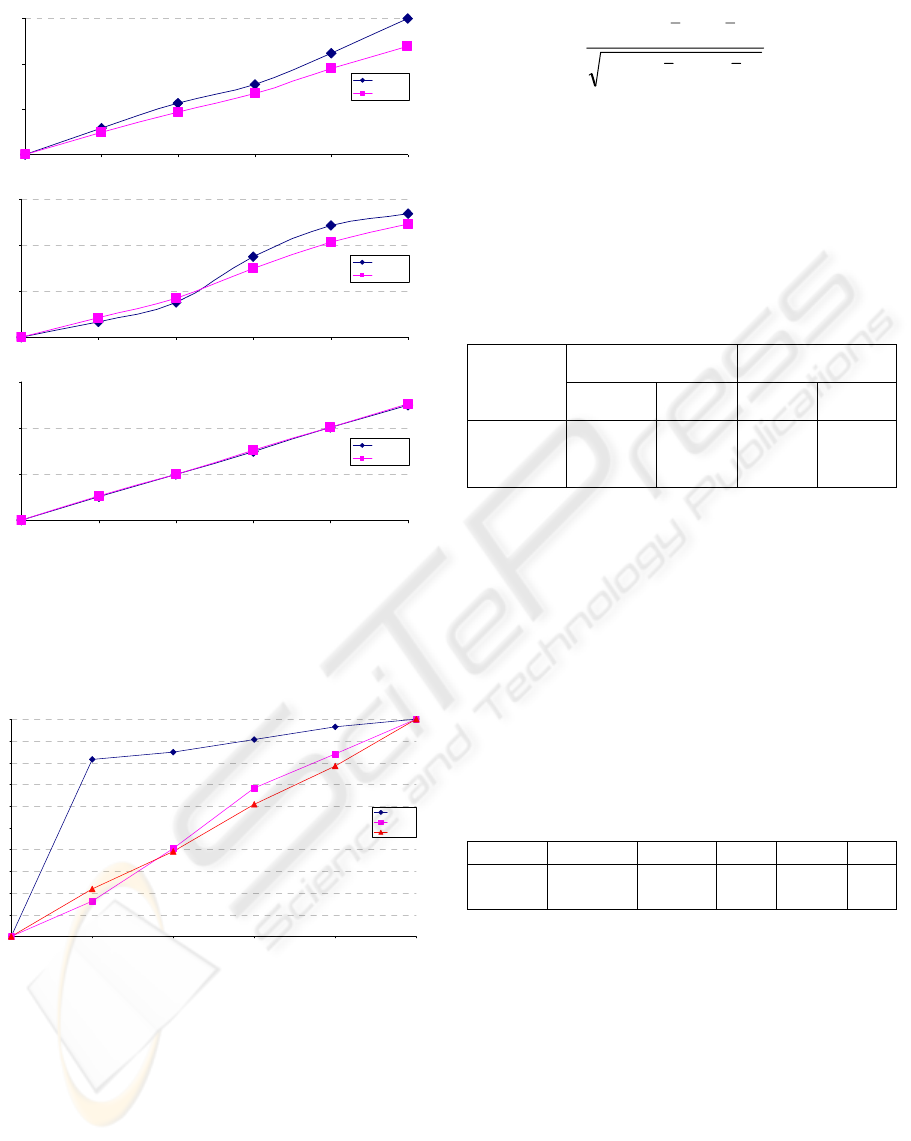
The results of the evaluation tests are given below.
Tests include the binary and grey-level centroids.
For each movement increment the two figures are
presented, as described below.
Pixel difference between the starting image and
the consecutive images (at consecutive positions) –
for each position the value is calculated as the
average displacement of all 10 markers, while their
position is calculated as the average position in the
sequence of the 16 images grabbed at each position
in static conditions. The lines in these figures should
be as straight as possible.
The 0.01mm, 0.1mm, and 1mm increments for
2D tests are presented in Figure 1.
ROBOT TCP POSITIONING WITH VISION - Accuracy Estimation of a Robot Visual Control System
213
0,00
0,01
0,02
0,03
0,00 0,01 0,02 0,03 0,04 0,05
position [mm]
difference [pixel]
binar y
grey level
0,00
0,10
0,20
0,30
0,00 0,10 0,20 0,30 0,40 0,50
position [mm]
difference [pixel]
binar y
grey level
0,00
1,00
2,00
3,00
0,00 1,00 2,00 3,00 4,00 5,00
position [mm]
difference [pixel]
binar y
grey level
Figure 1: Pixel difference for 0.01mm (top), 0.1mm
(middle), and 1mm (bottom) increments.
Figure 2 compares normalized pixel differences
in grey-level images of a single marker.
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
123456
position
normalized
difference
0.01mm
0.1mm
1mm
Figure 2: Normalized differences of grey-level images for
each position comparing different increments.
A linear regression model was applied to
measured data, and the R
2
values calculated to asses
the quality of fit. The results are presented in Table 1
for 2D tests and in Table 2 for 3D tests. The R
2
value can be interpreted as the proportion of the
variance in y attributable to the variance in x (see
Eqn. 1), where 1 stands for perfect matching (fit)
and a lower value denotes some deviations.
2
22
2
)()(
))((
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−−
=
∑
∑
yyxx
yyxx
R
(1)
Considering the R
2
threshold of 0.994 we were
able to detect increments of the moving object in the
range of 1/5 of a pixel. The value of the threshold is
set to the value that gives a good enough
approximation of the linear regression model, to
ensure the applicable results of the measurements.
Table 1: Comparison of standard deviations and R
2
values
for different moving increments in 2D.
standard
deviation[mm]
R
2
increments
[mm]
binary
grey-
level
binary
grey-
level
0.01 0.045 0.027 0.4286 0.6114
0.1 0.090 0.042 0.8727 0.9907
1 0.152 0.069 0.9971 0.9991
The dynamic 2D test showed that when
comparing the centers of the markers of the IR-LED
array and the pixel areas of each marker in statically
and dynamically (linear guide moving at full speed)
grabbed images there is a difference in center
positions and also the areas of markers in
dynamically grabbed images are slightly larger than
those of statically grabbed images.
Table 2 presents the differences of the centers of
the markers, and difference in sizes of the markers
of the statically and dynamically grabbed images.
Table 2: Comparison of the images grabbed in static and
dynamic mode.
X Y width height area
static 484.445 437.992 6 6 27
dynamic 484.724 437.640 7 6 32
Regarding the results presented in Table 2, the
accuracy of the position in direction x of
dynamically grabbed images comparing to statically
grabbed is in the range of 1/3 of a pixel, due to the
gravity centre shift of pixel area of marker during
the movement of the linear guide.
4.2 3D Reconstruction Tests
We tested the static relative accuracy of the 3D
reconstruction of the IR-LED array movements by
linear drive. The test setup consisted of the two
calibrated Photonfocus cameras focused on the IR-
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
214
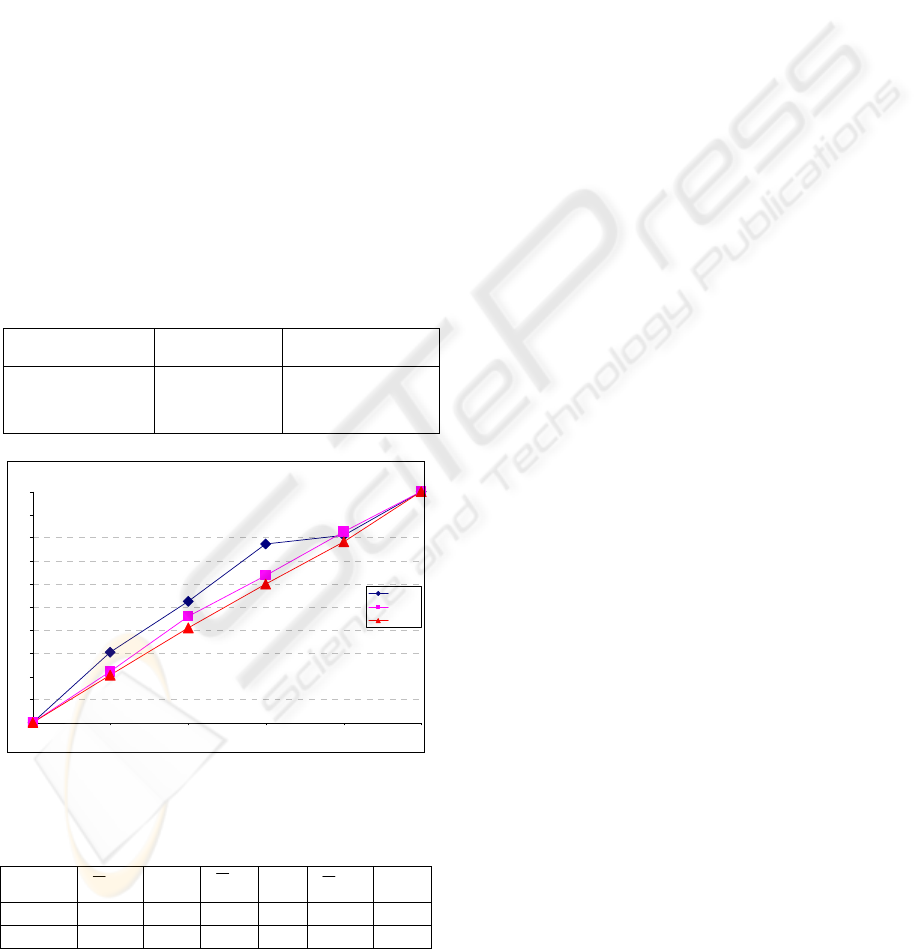
LED array attached to the linear drive which
exhibited precise movements of 0.01mm, 0.1mm
and 1mm. The mass centre points of 10 LEDs were
extracted in 3D after each movement and relative 3D
paths were calculated and compared to the linear
drive paths. Only grey-level images were
considered, due to the better results obtained in 2D
tests, as stated in Figure 2 and in Table 1. The
0.01mm, 0.1mm, and 1mm increments for the 3D
tests are presented in Figure 3.
The accuracy in 3D is lower than in the 2D case,
due to calibration and reconstruction errors, and
according to the tests performed it is approximately
1/2 of a pixel.
Table 4 presents the results of the 3D dynamic
tests where the triangle area and side lengths a, b
and c, reconstructed from dynamically-obtained
images were compared to static reconstruction of the
same triangles. 10 triangles were compared, each
formed by a diode in IR-LED array. The average
lengths and the standard deviations are presented.
Table 3: Comparison of standard deviations and R
2
values
for different moving increments in 3D.
increments [mm]
standard
deviation [mm]
R
2
0.01 0.058 0.7806
0.1 0.111 0.9315
1 0.140 0.9974
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
123456
positi on
s
normal ized
difference
0.01 mm
0.1 mm
1 mm
Figure 3: Pixel difference in the 3D reconstruction.
Table 4: comparison of static and dynamic triangles. All
measurements are in mm.
a
σ
b
σ
c
σ
static 193.04 12.46 89.23 2.77 167.84 12.18
dynamic 193.51 12.43 89.03 2.77 167.52 12.03
We observe a significant standard deviation (up
to 7%) of triangle side lengths which we ascribe to
lens distortions since it is almost the same in the
dynamic and in the static case. The images and the
reconstruction in dynamic conditions vary only a
little in comparison to static ones.
5 CONCLUSIONS
We performed the 2D and 3D accuracy evaluation of
the 3D robot vision system consisting of 2 identical
1 Megapixel cameras. The measurements showed
that the raw static 2D accuracy (without any
subpixel processing approaches and lens distortion
compensation) is confidently as good as 1/5 of a
pixel. However, this is reduced to 1/2 of a pixel
when image positions are reconstructed in 3D due to
reconstruction errors.
In the dynamic case, the comparison to static
conditions showed that no significant error is
introduced with moving markers in both, 2D and 3D
environment. For the speed level of an industrial
robot the accuracy is though not reduced
significantly.
ACKNOWLEDGEMENTS
This work was supported by the European 6th FP
project Adaptive Robots for Flexible Manufacturing
Systems (ARFLEX, 2005-2008) and the Slovenian
Research Agency programme Computing structures
and systems (2004-2008).
REFERENCES
Arflex European FP6 project official home page:
http://www.arflexproject.eu
Faugeras, O., 1992. Three-Dimensional Computer Vision:
A geometric Viewpoint, The MIT Press.
Hutchinson, S., Hager, G., Corke, P.I., 1995. A tutorial on
visual servo control, Yale University Technical Report,
RR-1068.
Papa, G., Torkar, D., 2006. Investigation of LEDs with
good repeatability for robotic active marker systems,
Jožef Stefan Institute technical report, No. 9368.
Robson, D., 2006. Robots with eyes, Imaging and
machine vision-Europe, Vol. 17, pp. 30-31.
Ruf, A., Horaud, R., 1999. Visual servoing of robot
manipulators, Part I: Projective kinematics, INRIA
technical report, No. 3670.
Zhang, Z., 1998. A flexible new Technique for Camera
Calibration, Technical report, MSRTR-98-71.
Zuech, N., 2000. Understanding and applying machine
vision, Marcel Dekker Inc.
ROBOT TCP POSITIONING WITH VISION - Accuracy Estimation of a Robot Visual Control System
215
