
A GROWING FUNCTIONAL MODULE DESIGNED TO
TRIGGER CAUSAL INFERENCE
Jérôme Leboeuf Pasquier
Departamento de Ingeniería de Proyectos, CUCEI, Universidad de Guadalajara
Apdo. Postal 307, CP 45101, Zapopan, Jalisco, México
Keywords: Artificial brain, epigenetic robotics, autonomous control, learning system, growing neural network.
Abstract: “Growing Functional Modules” constitutes a prospective paradigm founded on the epigenetic approach
whose proposal consists in designing a distributed architecture, based on interconnected modules, that
allows the automatic generation of an autonomous and adaptive controller (artificial brain). The present
paper introduces a new module designed to trigger causal inference; its functionality is discussed and its
behavior is illustrated applying the module to solve the problem of a dynamic maze.
1 INTRODUCTION
1.1 The Epigenetic Approach
According to Epigenesis, introduced in
Developmental Psychology by Piaget (Piaget, 1970),
the emergence of intelligence in a system requires
such system to have a physical presence
(embodiment) that allows an interaction with the
environment (situatedness), furthermore this system
should hold an “epigenetic developmental process”
in charge of developing some specific skills to fulfill
particular goals. If extrapolating this theory to
Computer Science, Robotics constitutes the proper
application field as it provides both embodiment and
situatedness; then, an intelligent system performing
as the robot‘s controller could emulate the
“epigenetic developmental process”.
Formally introduced in (Leboeuf, 2005),
Growing Functional Modules (GFM) constitutes a
prospective paradigm founded on this epigenetic
approach. As a result, a GFM controller gradually
acquires the specialized abilities while trying to
satisfy some induced internal goals, which can be
interpreted as motivations.
1.2 The Concept of GF Module
In input, a module receives requests; each request
corresponds to the directive of reaching a specific
state. The corresponding finite set of states is
initially empty, but it gradually increases integrating
as a new state, any distinct values provided by
feedback. Furthermore, each module is assigned a
set of commands that allows it acting on its
environment, either directly by positioning some
actuators or indirectly by sending requests to other
modules. States transitions are achieved triggering
these commands. Hence, each module enclosed a
dynamic structure, typically a network of cells that
gradually grows to memorize the correlations
between these state transitions and a corresponding
sequence of commands.
The engine of the module is in charge of
retrieving an optimal sequence of transitions
connecting the current state to the requested one and
then, replicating it while triggering the
corresponding sequence of commands (propagation).
Obviously, the environment, commonly the real
world, does not present a deterministic behavior due
mainly, to an incomplete perception (the finite set of
sensors reflects only a fraction of the reality); but
also to errors associated to sensing (like round off,
precision of the sensors, mechanical imperfections
and external disturbances). So, when feedback
exhibits some minor differences between the
predicted behaviour and the obtained one, an
adaptation mechanism is in charge of adjusting the
current transitions; while, in case of major
differences, a new sequence of transitions may be
computed and then replicated.
GF modules have no previous learning phase;
learning and adaptation may occur at any time when
456
Leboeuf Pasquier J. (2007).
A GROWING FUNCTIONAL MODULE DESIGNED TO TRIGGER CAUSAL INFERENCE.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 456-463
DOI: 10.5220/0001643704560463
Copyright
c
SciTePress

propagation does not fit the previously acquired
behaviour. Nevertheless, to avoid a limitless
growing of the internal structure, this structure must
converge when interacting with a stable
environment, i.e. an environment in which for this
specific module the same causes produce the same
effects during a certain period of time.
As a result, a module constitutes an autonomous
entity able by its own to perform a specific class of
control. For instance, two recent papers describe the
RTR-Module and its improved version (Leboeuf,
2006) designed to perform basic automatic control;
its behavior is illustrated by the application to an
inverted pendulum.
1.3 The Concept of GFM Architecture
In addition to the ports dedicated to input requests,
to feedback and to output commands previously
mentioned, all modules incorporate an input-output
inhibition port that allows a module to prevent
propagation in another one. As a result, the
interconnection of modules through these
communication ports allows the elaboration of a
multi-purposes architecture.
An illustration of a GFM architecture including
six modules of three different types is described in
(Leboeuf, 2005). The corresponding controller
shows its ability to discover and handle the potential
functionalities of a virtual, mushroom shaped robot
including the control of the single leg’s steps, the
direction of the body and the orientation of the hat.
To induce learning of such functionalities, at least
one global goal is required at the top of the
architecture. In the case of the mushroom shaped
robot, such induced motivation corresponds to light
seeking.
In accordance with this approach, the GFM
“programming process” consists of graphically
designing the GFM architecture, i.e. interconnecting
a set of functional modules. Afterward, two C++
source files are automatically generated; they
contain the constructor of the controller and a
description of the serial communication protocol
between the controller and its associated application.
Compiling these two files and linking them with the
GFM library produce the GFM controller that
initiates its activity when connected to the
corresponding application (virtual or real). As a
result, this paradigm, though still in a development
phase, brings forward the possibility of setting up an
autonomous and adaptive controller replacing the
traditional programming task by the design and
training of a distributed architecture.
As a prospective computer science paradigm,
GFM offers several relevant aspects:
First, memory is the exclusive product of a
learning process;
Second, the acquired knowledge and its
processing engine are indivisible;
Third, adaptation to changing environments is
intrinsic;
Fourth, all the learning process is guided by the
satisfaction of global goals (that may be
interpreted as motivations).
Therefore, as a system’s architecture, GFM has a
propensity to introduce a more natural concept of
memory and knowledge processing.
2 THE CI-MODULE
2.1 Concept
Earlier, the conception and development of a new
GF module arises to satisfy the necessity of
controlling some specific hardware. Presently, the
proposal of its creation comes out from the
importance of causal inference in cognitive
psychology. This assertion and the subsequent
statements are inspired by the theories of cognitive
psychology concerning learning and memory
exposed in (Anderson, 1999).
There, causal inference appears to play a
fundamental role concerning adaptation since an
organism able to discover the cause of some
phenomenon also acquires the ability of predicting
and/or producing some behavior in its environment
and consequently, it is able to control some
particular aspects in order to satisfy its needs.
Moreover, causal inference allows facing more
complex situations than, for example, associative
learning and therefore seems to be involved in many
cognitive levels from simple action-reward activity
to language acquisition.
Such important role of causal inference justifies
its introduction as a new module of the Acting Area
in charge of triggering the corresponding sequence
of actions that satisfies a specific request from a
higher module (a process referred in the previous
paragraph as “producing some behavior”). Its
counterpart belonging to the Sensing Area and in
charge of interpreting multiple feedbacks from
sensors (referred as “predicting some behavior”) is
still under study and will not be described in the
present paper. Hence, active and passive
functionalities of causal inference mentioned above
A GROWING FUNCTIONAL MODULE DESIGNED TO TRIGGER CAUSAL INFERENCE
457
are partitioned to be integrated to the GFM
architecture.
In robotics, GFM’s field of application, causal
inference should play a key role in planning because
it requires the robot to elaborate an optimum path
from an initial state corresponding to its current
situation toward a final one that matches the
requested conditions.
2.2 Achieving Propagation
The internal structure of a CI-Module is represented
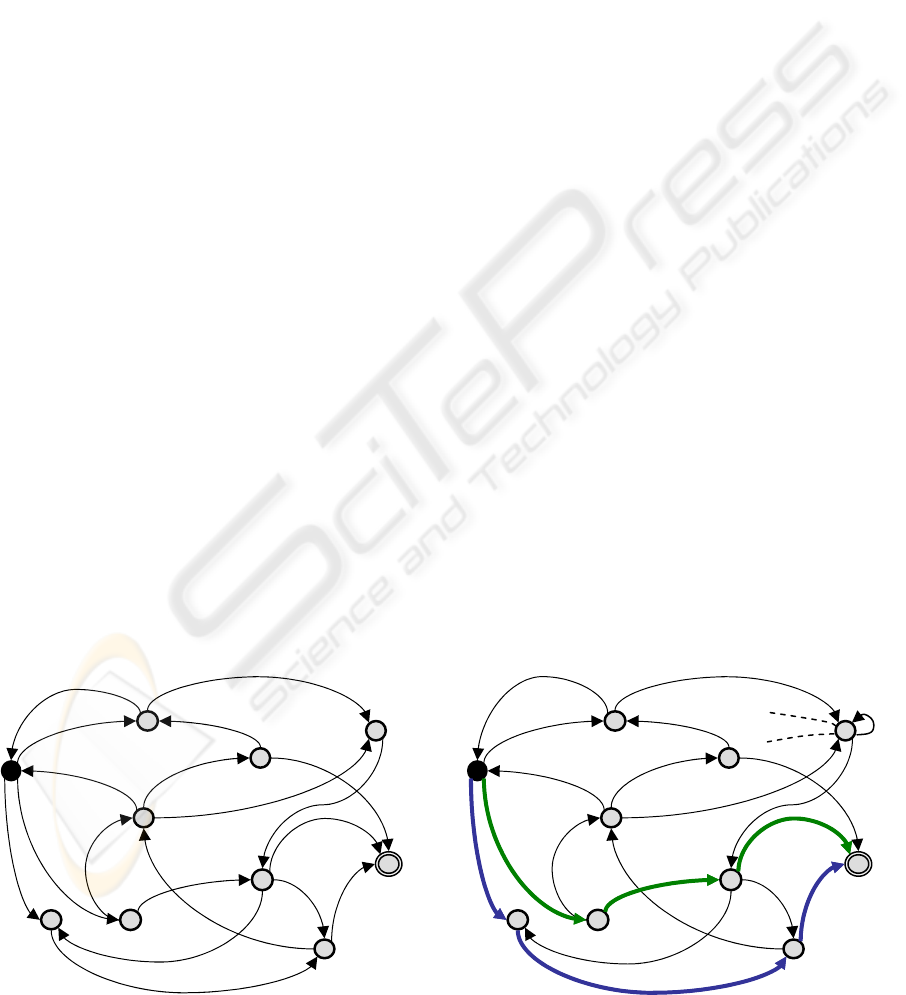
as a state graph, as illustrated on figure 1. The
transition from one state to another is obtained by
triggering the associated command. For example,
from the current state, identified with black color
and labeled with number ‘7’, it is possible to reach
the state labeled ‘6’ by triggering the command c
4
, at
least when the universe is fully deterministic. Then,
different sequences of commands allow, starting
from the current state, reaching the goal state labeled
with number ‘9’ and identified with a double circle.
For example, the sequences (c
1
c
1
c
2
), (c
1
c
1
c
1
c
4
),
(c
2
c
4
c
1
c
2
), (c
3
c
2
c
4
) among many others, comply
with this purpose. Internally, all states are defined
and validated as a result of the feedback values and
the goal state is given by the input request. Besides,
all commands belong to the set assigned to the
module during the designing phase.
As a consequence, propagation consists of
finding and applying the optimal sequence of
commands to reach the goal. The qualifier “optimal”
refers to the sequence offering the lowest cost while
considering that each command has an associated
cost. This problem is analogous to the search of the
shortest path in a graph considering that the weights
given here, represent the cost associated with the
commands. With the condition, presently verified,
that all weights are positive, Dijkstra’s algorithm
(Dijkstra, 1959) always encounters the optimal
solution to this problem. The principle of this
algorithm consists in repeatedly adding the most
economical edge from the currently visited nodes to
any unvisited ones, and iterating this process until
reaching the goal node. Several authors have
proposed alternative solutions with better
performances but with distinct hypothesis (Cooper et
al., 2000); so, at present, propagation is still guided
by an implementation of the Dijkstra’s algorithm. In
case, all commands have the same cost, then the best
path would have the lowest number of transitions; in
case several paths have the same number of
transitions (see blue and green paths represented on
figure 2) then the first one provided by the shortest-
paths algorithm will be chosen.
The costs mentioned previously in the
propagation process are obtained as follows: each
time it triggers a command, any GF acting module
provided an extra feedback value that either refers
the effort produced by the actuator to realize the
corresponding action or, in case of a lower module,
integrates all the subsequent efforts leading to
comply the corresponding request. This is an
important aspect as any module must prefer the
lowest solution. This feedback value produced by a
lower level set up the cost associated to the
transition. This cost may vary in time due to external
effects (see section 2.4), thus it must be updates
permanently as follows: each time a transition is
applied successfully, a new cost is assigned as the
half of the sum of the current cost and the returned
value.
2.3 Learning Transitions
To comply with the GFM paradigm, a module must
build up its internal structure from nothing, only
using the guidance of the feedback. At the
Figure 1: Graph of the internal structure of a CI-Module.
7
2
6
0
8
3
9
5
1
4
c
3
c
1
c
2
c
2
c
1
c
4
c
2
c
1
c
3
c
2
c
1
c
3
c
2
c
2
c
3
c
4
c
4
c
1
c
2
Figure 2: Two optimal paths to the goal state.
7
2
6
0
8
3
9
5
1
4
c
3
c
1
c
2
c
2
c
1
c
4
c
2
c
1
c
3
c
2
c
1
c
3
c
2
c
2
c
3
c
4
c
4
c
1
c
2
c
2
c
3
c
4
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
458
beginning, the initial state, given by the feedback,
corresponds to the local perception of the initial
value of a particular sensor. Then, from this state, a
randomly selected command is triggered and
eventually a new state discovered; this process is re-
iterated each time there is no path leading to the
requested goal, including the particular case when
this requested goal is still unknown and sometimes
non-existent; furthermore, each different value given
by the feedback is interpreted as a new state.
The graph resulting from this process is stored in
memory and permanently updated. According to the
illustration of figure 2, the only transition from state
‘1’ is correlated to the command c
1
, it comes out that
the commands c
2
and c
3
have not been tested yet and
that the command c
4
do not produce any transition.
Commands like c
4
should be ignored as they do not
generate a state transition nevertheless they must be
occasionally triggered to corroborate this fact. If
required, the graph is updated because, as exposed
next section, the environment is rarely deterministic.
2.4 Dealing with Non Determinism
The previous description of the CI-Module considers
the interaction with a deterministic environment,
nevertheless in the real world, an action often
produces uncertain effects due to
The imprecision of the sensory system that
engenders an incomplete representation of the
environment;
The presence of external and hidden effects;
The eventual presence of other entities that
possibly alter the current representation.
2.4.1 First Mechanism
Therefore, each time a command is triggered, the
new current state is determined by the supplied
feedback. If this state corresponds to the predicted
one, then propagation may continue in accordance
with the computed path; on the opposite, a new path,
starting from the new current state, determined by
the feedback value. This mechanism is fundamental
to deal with non determinism; an illustration is
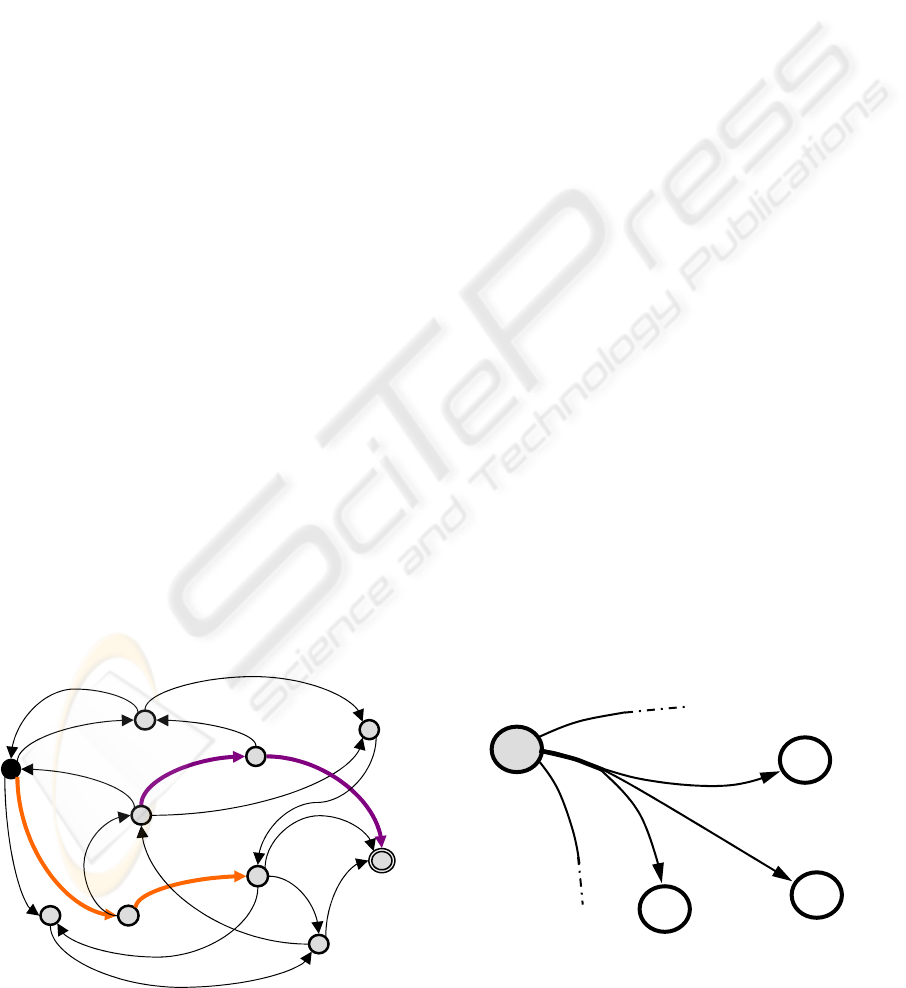
presented figure 3 where the predicted path starting
from state ‘7’, passing by ‘8’ and ‘4’ to reach the
goal state ‘9’ must be recomputed because state ‘5’
is specified by feedback instead of the predicted
state ‘4’; next, a new path is computed that consists
of states ‘5’, ‘0’ and finally ‘9’.
2.4.2 Second Mechanism
Moreover, in accordance with the previously
mentioned uncertainty of the environment, our
representation should not be deterministic but must
offer a distribution of probabilities corresponding to
the main outcomes of a command triggered from a
specific state. Such distribution of probabilities
should reflect the previous experience.
Several paradigms, in particular those based on
probability calculus like Markov Chains (Wai-Ki
and Michael, 2006) or Bayesian Networks (Jansen,
2001), build faithful representation of the
environment. Nevertheless, with regard to our
problem, they present the major inconvenient to
constitute passive processes, in the sense that they
do not act directly on the environment to establish a
resultant representation. In fact, these paradigms are
fine candidates to the sensing counterpart of the CI-
Module mentioned in section 2.1. Presently, an
alternative process has been implemented and this is
for two reasons: first to increase efficiency since one
criterion for growing functional modules is to be a
low cpu and memory consumer; next, because only
short term memory is required since it is assumed
that the response of the environment may frequently
change and so, its resulting feedback. In other
1
6
8
7
C
2
a
31
= 6
a
32
= 3
a
33
= 1
C
3
C
1
Figure 4: Memorizing different transitions generated by a
s
p
ecific command c
2
.
Figure 3: Re-computing the predicted path.
7
2
6
0
8
3
9
5
1
4
c
3
c
1
c
2
c
2
c
1
c
4
c
2
c
1
c
3
c
2
c
1
c
3
c
2
c
2
c
3
c
4
c
4
c
1
c
2
A GROWING FUNCTIONAL MODULE DESIGNED TO TRIGGER CAUSAL INFERENCE
459

words, the second implementation will favor fast
adaptation over long time memory.
The implementation of this process consists in
memorizing a small finite number t of different
transitions generated by a specific command c from
a given state s during a few last p intents and in
assigning the number a
i
of achievements to each
transition. For example, the transition depicted on
figure 4, reflects that during the last p attempts of
triggering the command c
2
from the state ‘1’, six
transitions reached the state ‘8’, three reached the
state ‘7’ and one the state ‘6’. Consequently, state
‘8’ that actually presents the highest reliability is
considered as the expected transition and is used to
compute the predicted path to reach the goal state. It
must be noticed that the sum of the achievements is
not equal to the number of attempts p because while
the successful alternative is incremented, all others
are decremented at the same time. Further, when an
alternative reaches the value p then, this means that
no other alternatives had appeared during the last p
attempts. Therefore, p reflects the sensibility to cope
with the changes that presents the environment: a
lower value of p produces a more dynamic behavior.
The transitions’ reliability is updated in the
following way: each time a command is triggered,
the resulting transition is compared to the t
memorized transitions. If found, its corresponding
reliability is incremented while the reliabilities of all
the other alternatives are decremented. If not found,
this new transition replaces the lowest memorized
one, and its reliability is set to 1. This mechanism
obviously favors the most recent outcomes of a
transition contrarily to a model based on historical
probability. In some way, experiments practiced on
rats dealing with mazes support this choice: the last
successful outcome obtains a relative predominance
over historical experience.
2.4.3 Additional Mechanisms
Three additional mechanisms are described in this
section; they all have been introduced to improve the
propagation in the internal structure of the CI-
Module.
The third mechanism consists of triggering, from
time to time, a command that, until now, has not
produced any transition from a particular state; like
for example in figure 2, the command c
4
triggered
from state ‘1’. This mechanism allows the detection
of potential paths that, on the contrary, would
remain ignored after being the object of an initial
failure. The implementation consists in periodically
triggering unproductive actions if any exist. In
practice, when a state has been activated a
predefined number of times, an unproductive action
is randomly selected and triggered.
The fourth mechanism consists of allowing
computation of the path using the best and the
second best transitions when their reliabilities are
relatively close. This mechanism reflects the fact
that two close reliabilities denote two good potential
transitions. But, this mechanism presents the
inconvenience to consequently increase the
processing time necessary to compute the optimum
path; therefore, its application is only optional.
The fifth mechanism has been introduced to take
into account the reliability of a transition. When
applying the Dijkstra algorithm, the choice of the
optimum path is achieved taking into account the
cost of the transition as previously described, but
also considering its reliability. This mechanism
clearly indicates that a longer but more reliable path
should be preferred to a shorter but more erratic one.
The implementation of this mechanism consists of
linearly increasing the cost according to the
reliability of the transition: the cost is doubled when
the reliability is minimal (i.e. equal to 1) and
unchanged when the reliability is maximum (i.e.
equal to p). Moreover, introducing reliability in the
evaluation of the potential paths contributes to make
the previous one obsolete.
A simplified pseudo-algorithm of the final
process is given figure 5; the presence of the
different mechanisms is also indicated.
3 COMPLIANCE
Any Growing Functional Module must satisfy three
main requirements to comply with the GFM
paradigm and thus, to be interconnected with other
modules and integrated into a GFM architecture.
These requirements, discussed in the present section,
contemplate the growing of the internal structure,
the interconnection with other modules and the
contribution of the module.
First, the internal structure of any module must be
initially nonexistent and designed to gradually grow
as the result of some learning mechanisms.
Moreover, these mechanisms must allow the
permanent adaptation of the internal structure
although this structure must stabilize when
performing in a stable environment. The
implementation of the CI-Module describes in
section 2 satisfies this requirement: when the initial
request is received as input, the first state is
originated; then new structures are created only in
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
460
response to new or inconsistent feedback which
means that, if the environment is stable, the internal
structure compound of states and transitions will not
grow. This leads to a conclusion about the
convergence of the structure since the local
adaptation of the transitions has no growing effect in
term of memory.
Second, the parameters that give a description of
the application to the module are reduced to the
standard ones including: the set of output
commands, the feedback value associated to the
current state and an input request with no specified
range. Due to the object oriented implementation,
any module derives from a common class that
includes all input-output ports; in consequence, the
CI-Module automatically fits the interconnection
requirement.
Thirdly, to illustrate its functionality and
contribution to the GFM architecture, the module
must achieve some generic control task, operating as
an autonomous entity that is able to communicate
with the application through the standard protocol.
The satisfaction of this requirement is exhibited next
section where the CI-Module is employed to achieve
the learning of a dynamic maze.
In addition to the previous requirements, it is
imperative to consider memory and processing costs
associated with the implementation of a module
since a GFM architecture is supposed to integrate
many modules. Concerning the CI-Module, the main
processing cost involves the algorithm that computes
the shortest path. The current implementation, based
on the standard definition of the Dijkstra’s
algorithm, offers a regular performance.
Nonetheless, (Fredman & Tarjan, 1987)
demonstrates that using a new structure called F-
Heaps the problem may be solved in near-linear
time: O( n.log(n) + m) where m and n respectively
represents the number of edges and vertexes.
Furthermore, (Matias et al., 1994) introduces the
notion of “approximate data structure” and proposes
a faster solution of the shortest path problem with
the condition of tolerating a small amount of error.
This offers a convenient alternative in case of
elevated cpu requirements as, in the case of GFM
modules, precision and exactitude requirements are
not essential because errors are considered part of
the learning process. Besides, the memory cost is
proportional to the number of states including for
each state a maximum number of p transitions, p
being the number of authorized commands; so, to
store a state and its p transitions, only 2p+28 bytes
are required with p commonly less than 10. Thus,
both, memory and cpu costs, appear to be
proportional to the number of achievable states.
Such number is in turn, related to a sufficient
learning time to produce a reliable behavior that
could be defined as a fixed minimum percentage of
correct responses of the system, typically ninety per
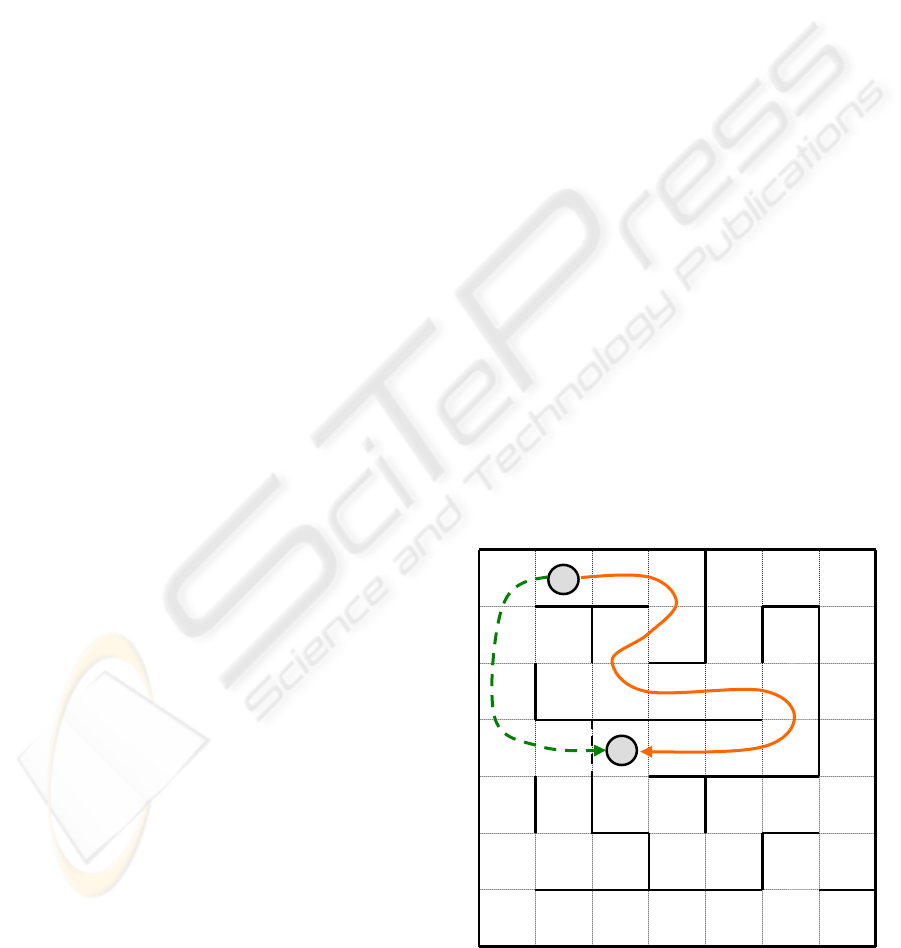
Figure 6: A typical maze used as an application where
letters ‘C’ and ‘R’ stands respectively for the curren
t
and the requested positions.
C
R
WHILE ContinueControl
TotalCost←0;
WaitFor(Request);
Get(Feedback);
FindOrCreate(CurrState,Feedback);
Found←Search(ShortPath); M
2,4,5
IF Found
Compute(Trans,PredState,Command); M
3
ELSE
Choose(Command);
WHILE CurrState#Request AND Command
Trigger(Command);
Get(Feedback,Cost);
TotalCost←TotalCost+Cost;
FindOrCreate(CurrState,FeedBack);
IF CurrState#PredState M
1
IF CurrState
Update(Trans,CurrState,Cost);
M
2,5
Search(ShortPath); M
2,4,5
ELSE
Create(Trans,CurrState,Cost);
Choose(Command);
ELSE
Reinforce(Trans,Cost);
Compute(Trans,PredState,Command); M
3
Return(TotalCost);
Figure 5: Simplified pseudo-algorithm of the internal
structure process corresponding to the CI-Module where
the mentioned mechanisms X are referred as M
X
.
A GROWING FUNCTIONAL MODULE DESIGNED TO TRIGGER CAUSAL INFERENCE
461

cent. Hence, the recommendation should be given to
the programmer, i.e. designer of the architecture, to
estimate the number of discrete states that will
generate a particular feedback from the environment.
Note that it could be assumed that a higher
number of commands will produce a larger internal
structure though there is no strict mathematical
relation between these concepts. This last assertion
may be inferred from the following example: all the
possible commands on actuators may be integrated
within a tiny structure of only two states
representing “mobility” and “immobility”.
Nevertheless, it could be assumed that, when
integrating the CI-Module with an architecture, it is
convenient to associate a reduced set of commands.
In conclusion, due to its compliance, the
corresponding C++ implementation of the CI-
Module may be added to the GFM library that
integrates all the fundamental components and
permits the design of an architecture for a GFM
controller.
4 APPLICATION
As mentioned before, each time a GF module is
developed a corresponding application must be
programmed and tested in parallel because the
module is supposed to be able to perform as a
controller on its own. Such an application represents
the challenge that directs the development of a
specific module.
In cognitive psychology, mazes constitute natural
tools to investigate causal inference. The obtained
results in this area have inspired in some way the
present study as, for example, the reference
introduced at the end of section 2.4.2. Actually, a
maze is the application defined to evaluate the
performance of the CI-Module. Nevertheless, the
behaviour of a rat in a maze is more complex than a
causal inference based control system because others
cognitive abilities like spatial representation take
part in the process.
In the current application, maze’s positions
correspond to states whose current one is provided
as feedback to the controller; meanwhile the set of
actions is composed of the elementary moves in
each of the four possible directions: north, south,
east and west. The task of the module consists of
learning the configuration of a particular maze as
illustrated on figure 6 and learning to satisfy a
request that stipulates which position to reach. Thus
a classic maze is implemented with three additional
characteristics:
First, the internal walls constituting the maze
may shift randomly from time to time;
Second, some “sliding effect” sometimes alters
the response to an action, in other words the
maze is not fully deterministic.
Third, the cost of each move is a function of its
direction.
Experimentally, the CI-Module is perfectly able
to perform the task of learning and solving the maze.
This is obvious since the maze offers a mirror
representation of the state graph that describes the
internal structure of the module. In fact, initially, the
maze has been conceived as an illustration of the
module’s expectations and then, it has been
employed to guide its development. Hence, for the
designer, the maze serves as a reference of the
ability of the CI-Module.
The major difficulty has been to deal with the
walls’ shifts in absence of tactile or visual
perception and thus, to discover a potential shorter
path as the emergent one indicated with dashed lines
on figure 6. In absence of any complementary
perception, the solution, given in section 2.4.3
consists of occasionally, triggering apparently
inefficient commands, thus giving the system the
ability of discovering new opportunities. Despite its
slowness, this mechanism satisfies the initial
requirement of adaptability inherent to the
architecture.
The tests have been realized running the single
module on a computer and the maze application on
another, both connected by a serial connection
implemented with the GFM standard protocol. The
results show that the version of the CI-Module
described in this paper, comply with all its expected
functionalities.
Finally, the importance of feedback timing must
be considered. In practice, the perception of a causal
inference depends of the proximity in space and
mostly time between an action and an effect. So, as
the delay increases, the consistency of the relation
decreases. The feedback is provided to the CI-
Module once the command has been fully
performed. In the case of commands triggered by
modules that involve requests to lower modules, the
feedback is provided when all the subsequent
commands have been applied and, consequently this
will increase the feedback’s delay. However, the
reaction of the environment is not always
instantaneous; for example, “the production of heat
as resulting from switching on a lamp” represents a
complex inference as a result of the extended delay
that occurs between both events. In such case, the
sensing Area is supposed to help providing the
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
462

interpretation of the phenomenon, but, at this time
there is no evidence to support this hypothesis.
5 CONCLUSIONS
The present paper introduced a novel Growing
Functional Module designed to perform causal
inference. Its conception and implementation are
fully described and its behavior illustrated by the
application to a dynamic maze problem.
The foremost conclusion is that this module
shows to be fully functional and compliant with the
requirements of any Growing Functional Module.
Consequently, it has been added to the GFM library
that incorporates all the components employed to
automatically build GFM controllers. Besides, the
internal structure of the CI-Module exhibits the
intrinsic qualities of the epigenetic approach: both
processes of learning and propagation are guided by
a (restricted) feedback of the environment.
Forthcoming works derived from the present one
include a module conceived as a counterpart of the
CI-Module designed to integrate the Acting Area.
The internal structure of this future module of the
Sensing Area is based on a Finite State Automaton.
Furthermore, an improved version of the present
module is also under study; it has a more
complicated internal structure based on an
Interpreted Petri Net.
REFERENCES
Piaget, J., 1970. Genetic Epistemology. Series of Lectures,
Columbia University Press, Columbia, New York.
Wai-Ki, C. & Michael, K.N., 2006. Markov Chains:
Models, Algorithms and Applications. Springer Eds.
Jansen, F.V., 2001. Bayesian Networks and Decision
Graphs, Springer Eds.
Leboeuf, J., 2005. Growing Functional Modules, a
Prospective Paradigm for Epigenetic Artificial
Intelligence. Lecture Notes in Computer Science 3563.
Springer, pp. 465-471.
Leboeuf, J., 2006. A Growing Functional Module
Designed to Perform Basic Real Time Automatic
Control. Publication pending in Lecture Notes in
Computer Science, Springer.
Leboeuf, J., 2006. Improving the RTR Growing Functional
Module. Proceedings of the 32nd Annual Conference
of the IEEE Industrial Electronics Society, IECON’06
Paris, pp. 3945-3950.
Leboeuf, J., 2005. Applying the GFM Prospective
Paradigm to the Autonomous and Adaptive Control of
a Virtual Robot. Lecture Notes in Artificial
Intelligence, Springer 3789, pp. 959-969.
Dijkstra, E.W., 1959. A Note on Two Problems in
Connexion with Graphs. Numerische Mathematik 1,
pp. 269-271.
Fredman, M.L. & Tarjan, R.E., 1987. Fibonacci Heaps
and their Use in Improved Network Optimization.
Journal of the ACM Vol. 34, pp 596-615.
Matias, Y., Vitter J.S. &Young, N.E., 1994. Approximate
Data Structure with Applications. Proceedings of the
ACM-SIAM Symposium, pp. 187-194
Cooper, C., Frieze, A., Mehlhorn, K. & Priebe, V., 2000,
Average-Case Complexity of Shortest Path Problems
in the Vertex-Potential Model.
Anderson, J.R., 1999. Learning and Memory, an
Integrated Approach. Wiley Eds.
A GROWING FUNCTIONAL MODULE DESIGNED TO TRIGGER CAUSAL INFERENCE
463
