AN INTELLIGENT MARSHALING PLAN BASED ON

MULTI-POSITIONAL DESIRED LAYOUT IN CONTAINER YARD

TERMINALS

Yoichi Hirashima

Dept. Media Science, Fac. Information Science and Technology, Osaka Institute of Technology

1-79-1 Kitayama, Hirakata-City, Osaka, 573-0196 Japan

Keywords:

Container marshaling, Block stacking problem, Q-learning, Reinforcement learning, Binary tree.

Abstract:

This paper proposes a new scheduling method for a marshaling in the container yard terminal. The proposed

method is derived based on Q-Learning algorithm considering the desired position of containers that are to

be loaded into a ship. In the method, 3 processes can be optimized simultaneously: rearrangement order of

containers, layout of containers assuring explicit transfer of container to the desired position, and removal plan

for preparing the rearrange operation. Moreover, the proposed method generates several desired positions for

each container, so that the learning performance of the method can be improved as compared to the conven-

tional methods. In general, at container yard terminals, containers are stacked in the arrival order. Containers

have to be loaded into the ship in a certain order, since each container has its own shipping destination and it

cannot be rearranged after loading. Therefore, containers have to be rearranged from the initial arrangement

into the desired arrangement before shipping. In the problem, the number of container-arrangements increases

by the exponential rate with increase of total count of containers, and the rearrangement process occupies large

part of total run time of material handling operation at the terminal. For this problem, conventional methods

require enormous time and cost to derive an admissible result. In order to show effectiveness of the proposed

method, computer simulations for several examples are conducted.

1 INTRODUCTION

In recent years, the number of shipping con-

tainers grows rapidly, and operations for layout-

rearrangement of container stacks occupy a large part

of the total run time of shipping at container termi-

nals. Since containers are moved by a transfer crane

driven by human operator, and thus, the container

operation is important to reduce cost, run time, and

environmental burden of material handling systems

(Siberholz et al., 1991). Commonly, materials are

packed into containers and each container has its own

shipping destination. Containers have to be loaded

into a ship in a certain desired order because they can-

not be rearranged in the ship. Thus, containers must

be rearranged before loading if the initial layout is dif-

ferent from the desired layout. Containers carried in

the terminal are stacked randomly in a certain area

called bay and a set of bays are called yard. When the

number of containers for shipping is large, the rear-

rangement operation is complex and takes long time

to achieve the desired layout of containers. Therefore

the rearrangement process occupies a large part of the

total run time of shipping. The rearrangement process

conducted within a bay is called marshaling.

In the problem, the number of stacks in each bay

is predetermined and the maximum number of con-

tainers in a stack is limited. Containers are moved by

a transfer crane and the destination stack for the con-

tainer in a bay is selected from the stacks being in the

same bay. In this case, a long series of movements of

containers is often required to achieve a desired lay-

out, and results (the number of container-movements)

that are derived from similar layouts can be quite dif-

ferent. Problems of this type have been solved by us-

ing techniques of optimization, such as genetic algo-

rithm (GA) and multi agent method (Koza, 1992; Mi-

nagawa and Kakazu, 1997). These methods can suc-

cessfuly yield some solutions for block stacking prob-

lems. However, they adopt the environmental model

different from the marshaling process, and do not as-

sure to obtain the desired layout of containers.

The Q-learning (Watkins and Dayan, 1992) is

known to be effective for learning under unknown

environment. In the Q-learning for generating mar-

shaling plan, all the estimates of evaluation-values for

pairs of the layout and movement of containers are

calculated. These values are called “Q-value” and Q-

234

Hirashima Y. (2007).

AN INTELLIGENT MARSHALING PLAN BASED ON MULTI-POSITIONAL DESIRED LAYOUT IN CONTAINER YARD TERMINALS.

In Proceedings of the Fourth Inter national Conference on Informatics in Control, Automation and Robotics, pages 234-239

DOI: 10.5220/0001643902340239

 SciTePress

table is a look-up table that stores Q-values. The input

of the Q-table is the plant state and the output is a Q-

value corresponding to the input. A movement is se-

lected with a certain probability that is calculated by

using the magnitude of Q-values. Then, the Q-value

corresponding to the selected movement is updated

based on the result of the movement. The optimal

pattern of container movements can be obtained by

selecting the movement that has the largest Q-value

at each state-movement pair, when Q-values reﬂect

the number of container movements to achieve the

desired layout. However, conventional Q-table has

to store evaluation-values for all the state-movement

pairs. Therefore, the conventional reinforcement

learning method, Q-learning, has great difﬁculties for

solving the marshaling problem, due to its huge num-

ber of learning iterations and states required to obtain

admissible operation of containers (Baum, 1999). Re-

cently, a Q-learning method that can generate mar-

shaling plan has been proposed (Hirashima et al.,

1999). Although these methods were effective several

cases, the desired layout was not achievable for every

trial so that the early-phase performances of learning

process can be degraded.

In this paper, a new reinforcement learning system

to generate a marshaling plan is proposed. The learn-

ing process in the proposed method is consisted of

two stages:

 determination of rearrangement order,

 selection of destination for removal containers.

Learning algorithms in these stages are independent

to each other and Q-values in one stage are referred

from the other stage. That is, Q-values are discounted

according to the number of container movement and

Q-table for rearrangement is constructed by using Q-

values for movements of container, so that Q-values

reﬂect the total number of container movements re-

quired to obtain a desired layout. Moreover, in the

end of stage

, selected container is rearranged into

the desired position so that every trial can achieve the

desired layout. In addition, in the proposed method,

each container has several desired positions in the ﬁ-

nal layout, and the feature is considered in the learn-

ing algorithm. Thus, the early-phase performances of

the learning process can be improved. Finally, effec-

tiveness of the proposed method is shown by com-

puter simulations for several cases.

2 PROBLEM DESCRIPTION

Fig.1 shows an example of container yard terminal.

The terminal consists of containers, yard areas, yard

transfer cranes, auto-guided vehicles, and port crane.

Containers are carried by trucks and each container is

Container terminal

Port crane

Yard transfer crane

Ship

Container

Yard area

Figure 1: Container terminal.

stacked in a corresponding area called bay and a set of

bays constitutes a yard area. Each bay has n

stacks

that m

containers can be laden, the number of con-

tainers in a bay is k, and the number of bays depends

on the number of containers. Each container is recog-

nized by an unique name c

(i = 1, ··· , k). A position

of each container is discriminated by using discrete

position numbers, 1, ··· , n

· m

. Then, the position

of the container c

is described by x

(1 ≤ i ≤ k, 1 ≤

≤ m

· n

), and the state of a bay is determined by

the vector, x = [x

, · ·· , x

2.1 Grouping

The desired layout in a bay is generated based on the

loading order of containers that are moved from the

bay to a ship. In this case, the container to be loaded

into the ship can be anywhere in the bay if it is on top

of a stack. This feature yields several desired layouts

for the bay. In the addressed problem, when contain-

ers on different stacks are placed at the same height in

the bay, it is assumed that the positions of such con-

tainers can be exchanged. Fig.2 shows an example

of desired layouts, where m

= n

= 3, k = 9. In the

ﬁgure, containers are loaded in the ship in the descen-

dent order. Then, containers c

, c

are in the same

group (Group1), and their positions are exchanged be-

cause the loading order can be kept unchanged after

the exchange of positions. In the same way, c

, c

are in the Group2, and c

, c

are in the Group3

where positions of containers can be exchanged. Con-

sequently several candidates for desired layout of the

bay are generated from the original desired-layout.

In addition to the grouping explained above, a

“heap shaped group” for n

containers at the top of

stacks in original the desired-layout (group 1) is gen-

erated as follows:

1. n

containers in group 1 can be placed at any

AN INTELLIGENT MARSHALING PLAN BASED ON MULTI-POSITIONAL DESIRED LAYOUT IN CONTAINER

YARD TERMINALS

235

A desired layout (original)

Bay

stack1

stack2

stack3

= 3

Layout candidates for bay

···

Grouping

Group1

Group2

Group3

Figure 2: Layouts for bay.

stacks if their height is same as the original one.

2. Each of them can be stacked on other n

− 1 con-

tainers when both of followings are satisﬁed:

(a) They are placed at the top of each stack in the

original disired-layout,

(b) The container to be stacked is loaded into the

ship before other containers being under the

container.

Other groups are the same as ones in the original

grouping, so that the grouping with heap contains all

the desired layout in the original grouping.

2.2 Marshaling Process

The marshaling process consists of 2 stages:

 se-

lection of a container to be rearranged, and

 re-

moval of the containers on the selected container in

. After these stages, rearrangement of the selected

container is conducted. In the stage

, the removed

container is placed on the destination stack selected

from stacks being in the same bay. When a container

is rearranged, n

positions that are at the same height

in a bay can be candidates for the destination. In ad-

dition, n

containers can be placed for each candi-

date of the destination. Then, deﬁning t as the time

step, c

(t) denotes the container to be rearranged at

t in the stage

. c

(t) is selected from candidates

= 1, · ·· , n

) that are at the same height in a

desired layout. A candidate of destination exists at a

bottom position that has undesired container in each

corresponding stack. The maximum number of such

stacks is n

, and they can have n

containers as can-

didates, since the proposed method considers groups

in the desired position. The number of candidates of

(t) is thus n

× n

. In the stage

, the container to

be removed at t is c

(t) and is selected from two con-

tainers c

= 1, 2) on the top of stacks. c

is on the

(t) and c

is on the destination of c

(t). Then, in the

stage

, c

(t) is removed to one of the other stacks in

the same bay, and the destination stack u(t) at time t

is selected from the candidates u

( j = 1, ·· · , n

− 2).

(t) is rearranged to its desired position after all the

s are removed. Thus, a state transition of the bay

is described as follows:

t+1



f(x

, c

(t)) (stage

)

f(x

, c

(t), u(t)) (stage

)

(1)

where f(·) denotes that removal is processed and x

t+1

is the state determined only by c

(t), c

(t) and u(t) at

the previous state x

. Therefore, the marshaling plan

can be treated as the Markov Decision Process.

Additional assumptions are listed below:

1. The bay is 2-dimensional.

2. Each container has the same size.

3. The goal position of the target container must be

located where all containers under the target con-

tainer are placed at their own goal positions.

4. k ≤ m

− 2m

+ 1

The maximum number of containers that must re-

moved before rearrangement of c

(t) is 2m

− 1 be-

cause the height of each stack is limited to m

. Thus,

assumption (4) assures the existence of space for re-

moving all the c

(t), and c

(t) can be placed at the

desired position from any state x

Initial layout of bay

case (a) case (b) case (c)

Marshaling

Step 1Step 1Step 1

Step 2Step 2Step 2

Step 3Step 3Step 3

Step 4Step 4Step 4

Step 5Step 5Step 5

desired layout for bay

positions in a bay

1112

Figure 3: Marshaling process.

Figure 3 shows 3 examples of marshaling process,

where m

= 3, n

= 5, k = 8. Positions of containers

are discriminated by integers 1, · ·· , 15. The ﬁrst con-

tainer to be loaded is c

and containers must be loaded

by descendent order until c

is loaded. In the ﬁgure,

a container marked with a 2 denotes c

, a container

marked with a  is removed one, and an arrowed

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

236

line links source and destination positions of removed

container. Cases (a),(b) have the same order of re-

arrangement, c

, c

, and the removal destinations

are different. Whereas, case (c) has the different or-

der of rearrangement, c

, c

. When no groups are

considered in desired arrangement, case (b) requires

5 steps to complete the marshaling process, and other

cases require one more step. Thus, the total number

of movements of container can be changed by the des-

tination of the container to be removed as well as the

rearrangement order of containers.

If groups are considered in desired arrangement,

case (b) achieves a goal layout at step2, case (a)

achieves at step3, case (c) achives at step4. If ex-

tended groups are considered, cases (a),(b) achive

goal layouts at step2 and case (c) achives at step4.

Since extended goal layouts include the non-extended

goal layouts, and since non-extended goal layouts in-

clude a non-grouping goal layout, equivalent or bet-

ter marshaling plan can be generated by using the ex-

tended goal notion as compared to plans generated by

other goal notions.

The objective of the problem is to ﬁnd the best

series of movements which transfers every container

from an initial position to the goal position. The goal

state is generated from the shipping order that is pre-

determined according to destinations of containers. A

series of movements that leads a initial state into the

goal state is deﬁned as an episode. The best episode is

the series of movements having the smallest number

of movements of containers to achieve the goal state.

3 REINFORCEMENT LEARNING

FOR MARSHALING PLAN

3.1 Update Rule of Q-values

In the selection of c

, the container to be rear-

ranged, an evaluation value is used for each candidate

= 1, · ·· , n

). In the same way, evaluation val-

ues are used in the selection of the container to be

removed c

and its destination u

( j = 1, ··· , n

− 2).

Candidates of c

is c

= 1, · ·· , n

). The evalua-

tion value for the selection of c

, c

and u

at the

state x are called Q-values, and a set of Q-values is

called Q-table. At the lth episode, the Q-value for

selecting c

is deﬁned as Q

(l, x, c

), the Q-value

for selecting c

is deﬁned as Q

(l, x, c

, c

) and

the Q-value for selecting u

is deﬁned as Q

(l, x, c

, u

). The initial value for both Q

, Q

is as-

sumed to be 0.

In this method, a large amount of memory space

is required to store all the Q-values referred in every

episode. In order to reduce the required memory size,

the length of episode that corresponding Q-values are

stored should be limited, since long episode often in-

cludes ineffective movements of container. In the fol-

lowing, update rule of Q

is described. When a series

of n movements of container achieves the goal state x

from an initial state x

, all the referred Q-values from

to x

are updated. Then, deﬁning L as the total

counts of container-movements for the corresponding

episode, L

min

as the smallest value of L found in the

past episodes, and s as the parameter determining the

threshold, Q

is updated when L < L

min

+ s(s > 0) is

satisﬁed by the following equation:

(l, x

, c

(t), c

(t), u(t)) =

(1− α)Q

(l − 1, x

, c

(t), c

(t), u(t))

+α[R+V

t+1

]



γmax

(l, x

, c

) (stage

)

γmax

(l, x

, c

(t), c

) (stage

)

(2)

where γ denotes the discount factor and α is the learn-

ing rate. Reward R is given only when the desired

layout has been achieved. L

min

is assumed to be inﬁn-

ity at the initial state, and updated when L < L

min

the following equation: L = L

min

In the selection of c

(t), the evaluation value

(l, x, c

(t), c

(t), u

) can be referred for all the

( j = 1·· ·n

− 2), and the state x does not change.

Thus, the maximum value of Q

(l, x, c

(t), c

(t), u

)

is copied to Q

(l, x, c(t)), that is,

(l, x, c

(t), c

(t)) =

max

(l, x, c

(t), c

(t), u

(3)

In the selection of c

(t), the evaluation value

(l, x, c

(t)) is updated by the following equations:

(l, x

, c

(t)) =



max

(l, x

, c

) + R (stage

)

max

(l, x

, c

(t), c

) (stage

)

(4)

In order to select actions, the ”ε-greedy” method

is used. In the ”ε-greedy” method, c

(t), c

(t) and a

movement that have the largest Q

(l, x, c

(t)), Q

(l,

x, c

(t), c

(t)) and Q

(l, x, c

(t), c

(t), u

) are selected

with probability 1−ε(0 < ε < 1), and with probability

ε, a container and a movement are selected randomly.

3.2 Learning Algorithm

By using the update rule, restricted movements and

goal states explained above, the learning process is

described as follows:

[1]. Count the number of containers being in the

goal positions and store it as n

AN INTELLIGENT MARSHALING PLAN BASED ON MULTI-POSITIONAL DESIRED LAYOUT IN CONTAINER

YARD TERMINALS

237

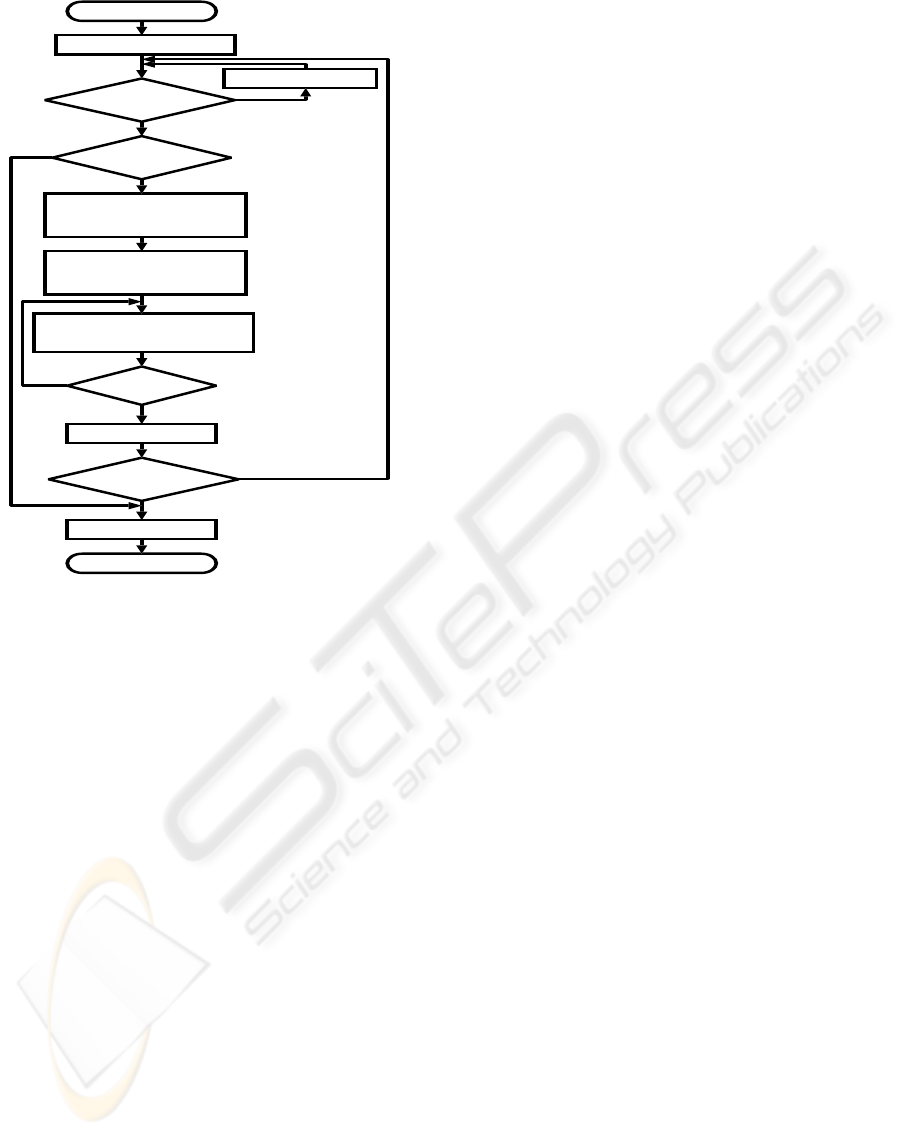
START

Initialize Q-values

Rearrange c

(t)

Rearrange c

(t)

Exist free c

(t)?

Select c

(t)

Select c

(t)

Save (x, c

(t), u

)

Save (x, c

(t), u

)

(Update Q

by eq.(3))

(Update Q

by eq.(4))

Exist c

(t)?

Move c

(t)

(Update Q

by eq.(2))

Save (x, c

(t), c

(t), u

)

Receive reward

Desired layout?

END

yes

Figure 4: Flowchart of the learning algorithm.

[2]. If n = k, go to [10]

[3]. Select c

(t) to be rearranged

[4]. Store (x, c

(t))

[5]. Select c

(t) to be removed

[6]. Store (x, c

(t), c

(t))

[7]. Select destination position u

for c

(t)

[8]. Store (x, c

(t), c

(t), u

)

[9]. Remove c

(t) and go to [5] if another c

(t) ex-

ists, otherwise go to [1]

[10]. Update all the Q-values referred from the initial

state to the goal state according to eqs. (2), (3)

A ﬂow chart of the learning algorithm is depicted

in Figure 4.

4 SIMULATIONS

Computer simulations are conducted for 2 cases, and

learning performances are compared for following

two methods:

(A) proposed method considering grouping with

heap,

(B) proposed method considering original grouping,

update rule without grouping (Hirashima et al.,

2005),

(D) method (E) considering original grouping.

(E) a learning method using, eqs. (2),(3) as the up-

date rule, which has no selection of the desired

position of c

(t) (Motoyama et al., 2001).

In methods (D),(E), although the stage

 has the

same process as in the method (A), the container to be

rearranged, c

(t), is simply selected from containers

being on top of stacks. The learning process used in

methods (D),(E) is as follows:

[1]. The number of containers being on the desired

positions is deﬁned as k

and count k

[2]. If k

= k, go to [6] else go to [3],

[3]. Select c

(t) by using ε-greedy method,

[4]. Select a destination of c

(t) from the top of

stacks by using ε-greedy method,

[5]. Store the state and go to [1],

[6]. Update all the Q-values referred in the episode

by eqs. (2),(3).

Since methods (D),(E) do not search explicitly the

desired position for each container, each episode is

not assured to achieve the desired layout in the early-

phase of learning.

In methods (A)-(E), parameters in the yard are set

as k = 18, m

= n

= 6 that are typical values of mar-

shaling environment in real container terminals. Con-

tainers are assumed to be loaded in a ship in descen-

dant order from c

to c

. Figure 5 shows a desired

layout for the two cases, and ﬁgure 6 shows corre-

sponding initial layout for each case. Other parame-

ters are put as α = 0.8, γ = 0.8, R = 1.0, ε = 0.8, s =

15.

The container-movement counts of the best solu-

tion and its averaged value for each method are de-

scribed in Table1. Averaged values are calculated

over 20 independent simulations. Among the meth-

ods, method (A) derives the best solution with the

smallest container-movements. Therefore method (A)

can improve the solution for marshaling as well as

learning performance to solve the problem.

Results for case 2 are shown in Fig. 7. In the ﬁg-

ure, horizontal axis shows the number of trials, and

vertical axis shows the minimum number of move-

ments of containers found in the past trials. Each

result is averaged over 20 independent simulations.

In both cases, solutions that is obtained by meth-

ods (A),(B) and (C) is much better as compared to

methods (D),(E) in the early-phase of learning, be-

cause methods (A),(B),(C) can achieve the desired

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

238

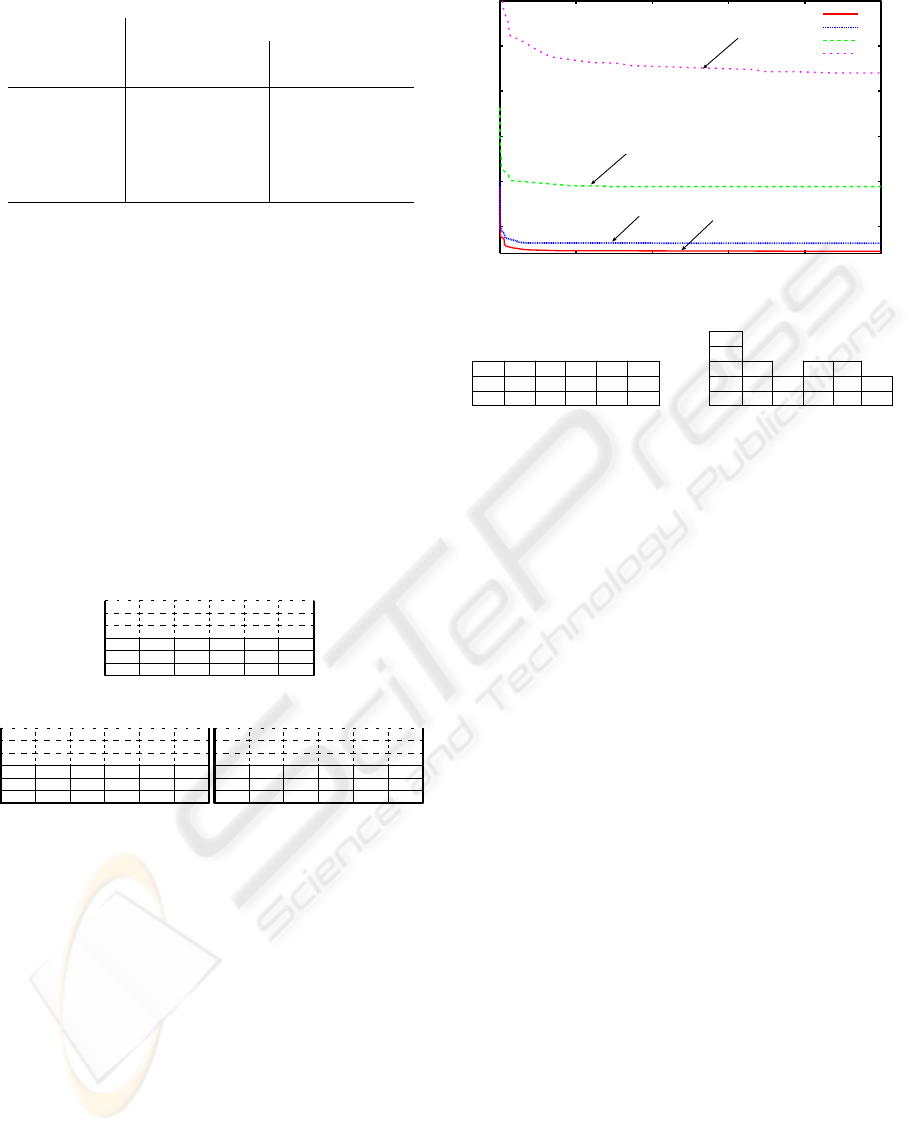
Table 1: The best solution of each method for cases 1, 2.

Case 1 Case 2

min. ave. min. ave.

counts value counts value

(A) 18 19.10 23 24.40

(B)

20 20.40 25 26.20

Method (C)

34 35.05 35 38.85

(D)

38 46.90 50 64.00

(E)

148 206.4 203 254.0

layout in every trial, whereas methods (D),(E) can-

not. Also, methods (A),(B) successfully reduces the

number of trials in order to achieve the speciﬁc count

of container-movements as compared to method (C),

since methods (A),(B) considers grouping and ﬁnds

desirable layouts than can easily diminish the number

of movements of container in the early-phase learn-

ing. Moreover, at 10000th trail the number of move-

ments of containers in method (A) is smaller as com-

pared to that in method (B) because, among the ex-

tended layouts, method (A) obtained better desired

layouts for improving the marshaling process as com-

pared to the layout generated by method (B). Desired

layouts generated by methods (A),(B) are depicted in

the Fig.8 for case 2.

Figure 5: A desired layout for cases 1,2.

Case 1 Case 2

Figure 6: Initial layouts for cases 1,2.

5 CONCLUSIONS

A new reinforcement learning system for marshaling

plan at container terminals has been proposed. Each

container has several desired positions that are in the

same group, and the learning algorithm is designed to

considering the feature.

In simulations, the proposed method could ﬁnd

solutions that had smaller number of movements

of containers as compared to conventional methods.

Moreover, since the proposed method achieves the de-

sired layout in each trial as well as learns the desir-

able layout, the method can generate solutions with

the smaller number of trials as compared to the con-

ventional method.

0 2000 4000

6000

8000 10000

Minimum step counts found in the past trials

Trials

(A)

(B)

(C)

(D)

Figure 7: Performance comparison for case 2.

Goal obtained by (B) Goal obtained by (A)

Figure 8: Final layouts of the best solutions for case 2.

REFERENCES

Baum, E. B. (1999). Toward a model of intelligence as an

economy of agents. Machine Learning, 35:155–185.

Hirashima, Y., Iiguni, Y., Inoue, A., and Masuda, S. (1999).

Q-learning algorithm using an adaptive-sized q-table.

Proc. IEEE Conf. Decision and Control, pages 1599–

1604.

Hirashima, Y., takeda, K., Furuya, O., Inoue, A., and Deng,

M. (2005). A new method for marshaling plan using a

reinforcement learning considering desired layout of

containers in terminals. Preprint of 16th IFAC World

Congress, pages We–E16–TO/2.

Koza, J. R. (1992). Genetic Programming : On Program-

ming Computers by means of Natural Selection and

Genetics. MIT Press.

Minagawa, M. and Kakazu, Y. (1997). An approach to

the block stacking problem by multi agent coopera-

tion. Trans. Jpn. Soc. Mech. Eng. (in Japanese), C-

63(608):231–240.

Motoyama, S., Hirashima, Y., Takeda, K., and Inoue, A.

(2001). A marshalling plan for container terminals

based on reinforce-ment learning. Proc. of Inter.

Sympo. on Advanced Control of Industrial Processes,

pages 631–636.

Siberholz, M. B., Golden, B. L., and Baker, K. (1991). Us-

ing simulation to study the impact of work rules on

productivity at marine container terminals. Comput-

ers Oper. Res., 18(5):433–452.

Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-

chine Learning, 8:279–292.

AN INTELLIGENT MARSHALING PLAN BASED ON MULTI-POSITIONAL DESIRED LAYOUT IN CONTAINER

YARD TERMINALS

239