TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A

SINGLE STEERING INPUT

Control Using Reference Time-Scaling

alint Kiss and Emese Sz

adeczky-Kardoss

Department of Control Engineering and Information Technology

Budapest University of Technology and Economics

Magyar Tud

osok krt. 2, Budapest, Hungary

Keywords:

Time-scaling, wheeled mobile robot, ﬂatness, motion planning, tracking control.

Abstract:

This paper presents a time-scaling based control strategy of the kinematic model of wheeled mobile robots

with one input which is the steering angle. The longitudinal velocity of the mobile robot cannot be inﬂuenced

by the controller but can be measured. Using an on-line time-scaling, driven by the longitudinal velocity of

the robot and its time derivatives, one can achieve exponential tracking of any sufﬁciently smooth reference

trajectory with non-vanishing velocity. The price to pay is the modiﬁcation of the traveling time along the

reference trajectory according to the time-scaling. The measurement of the time derivatives of the velocity is

no longer necessary if the tracking controller is designed to the linearized tracking error dynamics.

1 INTRODUCTION

The kinematic model of a wheeled mobile robot

(WMR) has generally two inputs namely the longitu-

dinal velocity of the rear axis midpoint and the steer-

ing angle of the front wheels. Several strategies are

applied to control such WMRs with these two inputs

including the tracking error transformation based con-

trol reported by (Dixon et al., 2001), the sliding mode

controller based solution proposed by (Benalia et al.,

2003), and the behavior based control strategy studied

by (Gu and Hu, 2002). An important property of the

model is its differential ﬂatness (Fliess et al., 1995;

Fliess et al., 1999) implying its dynamic feedback lin-

earizability (with a singularity at zero velocities).

However, situations may occur where the longitu-

dinal velocity of the WMR is not generated by a feed-

back controller, but by an external source. A practical

example of this scenario is the tracking problem re-

lated to a passenger car without automatic gear. In

such a situation the human driver needs to generate

the velocity of the car with an appropriate manage-

ment of the gas, clutch, and break pedals while the

tracking controller may inﬂuence only the angle of

the steered wheels. The kinematic model obtained

in such a situation is no longer differentially, but or-

bitally ﬂat (Respondek, 1998; Guay, 1999), since one

of the inputs is lost.

The control problem is still the tracking of the ref-

erence trajectory but this tracking may become im-

possible if the velocity of the reference WMR mov-

ing along the reference path is always superior to the

real velocity generated by the driver. The opposite is

also possible such that the velocity of the reference

WMR is always inferior to the real velocity gener-

ated by the driver. Nevertheless it is expected that

the path of the controlled WMR joins the path of the

reference WMR for any velocity proﬁle generated by

the driver. To achieve exponential tracking in both

cases, this paper suggests a time-scaling of the refer-

ence path. This time-scaling uses the measurement

of the velocity generated by the driver and eventually

its time derivatives. A practical mean to obtain these

measurements is the use of the ABS signals available

on the CAN bus of the vehicle or the use of alternative

sensors (e.g. accelerometers).

Recall that time-scaling is a commonly used con-

cept to ﬁnd optimal trajectories, to cope with input

saturation, to reduce tracking errors, and to establish

equivalence classes of dynamical systems.

One may use off-line time-scaling methods to

ﬁnd the time optimal trajectories for robot manipu-

lators (Hollerbach, 1984) or for autonomous mobile

vehicles (Cuesta and Ollero, 2005). The problem with

these off-line methods is that no sufﬁcient control in-

put margins are always assured for the closed loop

Kiss B. and Szádeczky-Kardoss E. (2007).

TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A SINGLE STEERING INPUT - Control Using Reference Time-Scaling.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 86-93

DOI: 10.5220/0001644200860093

 SciTePress

control during the tracking. Other algorithms use

therefore on-line trajectory time-scaling for robotic

manipulators to change the actuator boundaries such

that sufﬁcient margin is left for the feedback con-

troller (Dahl and Nielsen, 1990).

Another concept is to use the tracking error in-

stead of the input bounds in order to modify the

time-scaling of the reference path (L

evine, 2004;

adeczky-Kardoss and Kiss, 2006). These methods

change the traveling time of the reference path ac-

cording to the actual tracking error by decelerating if

the movement is not accurate enough and by acceler-

ating if the errors are small or vanish.

Time-scaling is also introduced related to the no-

tion of orbital ﬂatness deﬁned in (Fliess et al., 1999)

where a Lie-B

acklund equivalence of dynamical sys-

tems is established such that the transformation in-

volved may change the time according to which the

systems evolve. Another approach that relates time-

scaling to feedback linearization is reported in (Sam-

pei and Furuta, 1986).

The remaining part of the paper is organized as

follows. The next section presents the kinematic mod-

els of the WMRs. Section 3 studies brieﬂy the ﬂatness

properties of the models. Section 4 presents a sim-

ple motion planning method. The time-scaling con-

cept is introduced in Section 5. Two tracking feed-

back laws, both using time-scaling are reported in

Section 6. Simulation results are presented in Sec-

tion 7 and a short conclusion terminates the paper.

2 KINEMATIC WMR MODELS

Let us introduce some notations ﬁrst. Figure 1 depicts

a WMR in the xy horizontal plane. Let us suppose

that the Ackermann steering assumptions hold true,

hence all wheels turn around the same point (denoted

by P) which lies on the line of the rear axle. It follows

that the kinematics of the robot can be fully described

by the kinematics of a bicycle ﬁtted to the longitudinal

symmetry axis of the vehicle (see Figure 1). The co-

ordinates of the rear axle midpoint are given by x and

y. The orientation of the car with respect to the x axis

is denoted by the angle θ, hence the WMR evolves

on the conﬁguration manifold R

× S = SE(2). The

angle of the front wheel of the bicycle with respect to

the longitudinal symmetry axis of the robot is denoted

by ϕ. We consider u

= ϕ as an input. The longitu-

dinal velocity of the rear axle midpoint is denoted by

if it is a control input (two input case) and by v

car

if not (one input case).

The distance l between the front and rear axles

equals to one. Then the model equations can be ob-

( )xy,

Figure 1: Notations of the kinematic model.

tained after some elementary considerations which

result (see also for example (Rouchon et al., 1993;

Cuesta and Ollero, 2005))

˙x = u

cosθ (1)

˙y = u

sinθ (2)

θ = u

tanu

. (3)

Since time-scaling is involved in the sequel, we pre-

cise that the time in this system is denoted by t and ˙x

denotes the time derivative of the function x(t) such

that

t = 1.

Consider now the case where the longitudinal ve-

locity is not a control input but an external signal v

car

which is generated by the driver or by any other mean

such that the controller has no inﬂuence on its evo-

lution. The corresponding model with one input is

deﬁned by the equations

˙x = v

car

cosθ (4)

˙y = v

car

sinθ (5)

θ = v

car

tanu

. (6)

Consider now a time different from the time t, de-

noted by τ. Based on (1)-(3), let us deﬁne a model

evolving with the time τ and given by the equations

′

= u

τ,1

cosθ

(7)

′

= u

τ,1

sinθ

(8)

′

= u

τ,1

tanu

τ,2

(9)

where the subscript τ denotes the dependence on the

time τ and x

′

is the derivative of the function x

(τ)

with respect to τ. (No subscript is used for variables

dependent on time t except cases where the distinction

is necessary). It is obvious that τ

′

= 1 as

t = 1.

3 FLATNESS OF THE MODELS

One can easily verify or check in the literature (Rou-

chon et al., 1993; Fliess et al., 1995) that the

TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A SINGLE STEERING INPUT - Control Using

Reference Time-Scaling

model (1)-(3) (respectively (7)-(9)) is differentially

ﬂat, hence it can be linearized by a dynamic feedback

and a coordinate transformation. The ﬂat output is

given by x and y (respectively x

and y

The differential ﬂatness property of the models

can be exploited both for motion planning and track-

ing purposes. Given a reference trajectory x

ref

(t) and

ref

(t) for the ﬂat output variables x and y, which are

at least two times differentiable with respect to the

time t, one can determine the time functions of θ

ref

1,ref

, and u

2,ref

which satisfy (1)-(3) according to a

mapping

ref

,..., ¨x

ref

,..., ¨y

ref

} → {θ

ref

1,ref

2,ref

The same holds true for the model (7)-(9) evolving

with the time τ hence there exists a mapping

τ,ref

,...,x

′′

τ,ref

,...,y

′′

τ,ref

} →

{θ

τ,ref

τ,1,ref

τ,2,ref

}. (10)

The model (4)-(6) is not differentially, but orbitally

ﬂat for v

car

≡ 1 as shown by (Guay, 1999).

4 MOTION PLANNING

The motion planning is done for the system (7)-(9) ex-

ploiting its differential ﬂatness property. The motion

planning realizes the mappings

τ → {x

τ,ref

′

τ,ref

′′

τ,ref

} (11)

τ → {y

τ,ref

′

τ,ref

′′

τ,ref

} (12)

for τ ∈ [0,T] where T is the desired traveling time

along the path such that the mapping (10) allows then

to calculate the time functions of the remaining vari-

ables of the model.

Several motion planning schemes can be used to

realize (11) and (12). One may want to solve an ob-

stacle avoidance problem in parallel with the genera-

tion of the references (Cuesta and Ollero, 2005). For

the sake of simplicity, seventh degree polynomial tra-

jectories are considered in this paper such that

τ,ref

∑

i=0

x,i

, y

τ,ref

∑

i=0

y,i

. (13)

The coefﬁcients are obtained as solutions of a set

of linear algebraic equations determined by the con-

straints that the polynomials and their three succes-

sive derivatives must satisfy at τ = 0 and τ = T. No-

tice that the non-zero constraints are no longer re-

spected in the scaled time t for the derivatives of the

references unless

τ ≡ 1. It follows in particular that

the constraints imposed on the longitudinal velocities

at τ = 0 (respectively at τ = T) will be scaled by

τ(0)

(respectively by

τ(t(T)).

The motion planning can be done off-line prior

to the tracking and the time-scaling does not need

the redesign of the reference. It follows that more

involved methods can be also applied including the

one involving continuous curvature pathes with Fres-

nel integrals (Fraichard and Scheuer, 2004).

5 TIME-SCALING

A time-scaling law, which is deﬁned by the mapping

t 7→ τ(t) or by its inverse τ 7→ t(τ) can be obtained

based on the following consideration. Rewrite (4)-(6)

dx = v

car

dt cosθ (14)

dy = v

car

dt sinθ (15)

dθ = v

car

dt tanu

. (16)

Similarly, rewrite also (7)-(9) as

= u

τ,1

dτcosθ

(17)

= u

τ,1

dτsinθ

(18)

dθ

= u

τ,1

dτtanu

τ,2

. (19)

Consider now the model equations and the following

relations obtained from (14)-(16) and (17)-(19) for the

inputs of the models

dτ

= t

′

τ,1

car

= u

τ,2

. (20)

This allows to determine a unique trajectory of the

system (4)-(6) for a trajectory of the system (7)-(9)

if the time function v

car

(t) and the initial conditions

are given, and one supposes non-vanishing velocity

functions v

car

and u

τ,1

. As far as the initial condi-

tions are considered one may, for instance, suppose

that x(0) = x

(0), y(0) = y

(0), θ(0) = θ

(0). The

relations in the other direction are similar and read

dτ

τ =

car

τ,1

τ,2

= u

. (21)

The following proposition summarizes the properties

of the time-scaling for trajectories with strictly posi-

tive (respectively negative) velocities.

Proposition 1 Suppose that one considers trajecto-

ries of the different models of the kinematic car such

that the velocities v

car

and u

τ,1

are both strictly pos-

itive (respectively strictly negative). Then the time-

scaling t 7→ τ(t) and τ 7→ t(τ) deﬁned by (20)-(21)

satisfying t(0) = τ(0) are such that the functions τ(t)

and t(τ) are strictly increasing functions of their ar-

guments (the scaled time never rewinds).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

This property is a general requirement for mean-

ingful time-scaling and it is satisﬁed both for forward

and backward motions of the car. The time-scaling

has a singularity if the car is in idle position.

Note that for a ﬁxed velocity time function v

car

(t),

the time-scaling can be inﬂuenced by u

τ,1

, one of the

inputs of the ﬂat model evolving with τ. Observe

moreover that for ﬁxed v

car

these relations do not de-

ﬁne a one-to-one correspondence between the sets of

trajectories of the respective systems and the number

of inputs is not preserved, hence they are not Lie-

acklund isomorphisms (Fliess et al., 1999).

Suppose that the references are obtained for (7)-

(9) and one disposes of the time functions x

τ,ref

, x

′

τ,ref

′′

τ,ref

, y

τ,ref

, y

′

τ,ref

, y

′′

τ,ref

. (A simple method is given

in preceding section for the planning of the reference

motion.) The time-scaling is deﬁned by the mappings

τ,ref

,...,x

′′

τ,ref

} → {x

ref

(t),..., ¨x

ref

(t)} (22)

τ,ref

,...,y

′′

τ,ref

} → {y

ref

(t),..., ¨y

ref

(t)} (23)

which can be determined using (21) since

τ(t) =

car

ϑ,1

dϑ τ(0) = t(0) = 0 (24)

car

τu

t,1

(25)

˙v

car

τu

t,1

τ ˙u

t,1

(26)

allow to express τ(t),

τ, and

τ. Then

ref

(t) = x

τ,ref

(τ(t)) (27)

˙x

ref

(t) = x

′

τ,ref

(τ(t))

τ (28)

¨x

ref

(t) = x

′′

τ,ref

(τ(t))

+ x

′

τ,ref

(τ(t))

τ (29)

and one obtains similar expressions for the higher or-

der time derivatives and for the mapping (23).

Suppose that a reference trajectory is calculated

according to the time τ and that one is looking for

an open loop control of the real car to follow the ge-

ometry of the reference trajectory. Assume moreover

that the reference trajectory is calculated based on the

initial conditions of the real car. Then the open loop

control signal u

(t) can be calculated from the refer-

ence u

τ,2,ref

using the time-scaling deﬁned by (20).

Notice however that the real traveling time for a ref-

erence trajectory according the timet will be obtained

as t(T). If the driver generating v

car

accelerates with

respect to the reference trajectory than T > t(T). If

he/she is more careful than the algorithm providing

the value for T than T < t(T).

6 TRACKING FEEDBACK

DESIGN

Two tracking controllers are presented in this section.

The ﬁrst one is based on the ﬂatness property of the

model with two inputs and requires the measurement

of the car velocity and its two successive time deriva-

tives. Measurement of the acceleration and its time

derivative may be prohibitive for real applications.

Therefore another tracking feedback is also suggested

which is designed for a system obtained by linearizing

the tracking error dynamics around the reference tra-

jectory achieving only local stability of the reference

trajectory.

6.1 Flatness-Based Tracking using

Time-Scaling

The system (1)-(3) can be linearized by dynamic feed-

back in virtue of its differential ﬂatness property. The

resulting linear system is two chains of integrators

(3)

= ω

(3)

= ω

. (30)

Suppose that one speciﬁes the tracking behavior in

terms of the tracking errors e

= x − x

ref

and e

y− y

ref

such that the differential equations

(3)

+ k

x,2

¨e

+ k

x,1

˙e

+ k

x,0

= 0 (31)

(3)

+ k

y,2

¨e

+ k

y,1

˙e

+ k

y,0

= 0 (32)

hold true. The coefﬁcients k

a,i

(a ∈ {x, y}, i = 0,1,2)

are design parameters and have to be chosen such that

the corresponding characteristic polynomials have all

their roots in the left half of the complex plane. These

linear differential equations deﬁne another (tracking

feedback) for (30)

= x

(3)

ref

− k

x,2

¨e

− k

x,1

˙e

− k

x,0

(33)

= y

(3)

ref

− k

y,2

¨e

− k

y,1

˙e

− k

y,0

. (34)

Consider now the model described by (4)-(6).

This single input model is not differentially ﬂat, hence

cannot be linearized by feedback. It follows that the

ﬂatness property cannot be (directly) used to solve the

tracking problem.

Let us study the possibility to use the time-scaling

deﬁned above to achieve the desired tracking behavior

for the non-differentially ﬂat model (4)-(6) with one

input.

The idea is to use the differentially ﬂat model (7)-

(9) to solve the motion planning problem with the

time τ. Then one would use a tracking feedback con-

troller designed again for the ﬂat model which pro-

duces u

τ,1

and u

τ,2

. The signal u

τ,1

produced by the

controller is used to drive the time-scaling of the ref-

erence trajectory designed for the time τ according

to (21). The control loop is illustrated in Figure 2 for

the model (4)-(6) where the controller provides u

= ϕ

to the single input model. The tracking feedback is

TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A SINGLE STEERING INPUT - Control Using

Reference Time-Scaling

( )xy,

car

driver

tracking

controller

time

scaling

car

ref

in t

ref

in t

t,1

xy, ,q

motion

planning

Figure 2: Tracking controller with time-scaling.

designed using the ﬂatness property of the model with

two inputs. Deﬁne ﬁrst the dynamics for the feedback

= ζ

= v

(35)

= v

ϕ = ζ

(36)

= ζ

(37)

where ζ

, ζ

, and ζ

are the (inner) states of the feed-

back. Observe that ζ

and v

give precisely the deriva-

tives of u

which need to realize the time-scaling

in (24)-(26), hence no numerical differentiation is

needed.

The inputs v

and v

of the feedback dynamics

must be determined such that the tracking errors e

(t)

and e

(t) satisfy (31) and (32), respectively.

For, one needs to determine ﬁrst x, ˙x, ¨x, x

(3)

, y, ˙y,

¨y, and y

(3)

as functions of x, y, θ, ζ

, ζ

, and ζ

which

are the states of the closed loop system including the

measured states of the kinematic car model, and the

states of the feedback (35)-(37). After some cumber-

some but elementary differentiations one obtains

˙x = ζ

cosθ (38)

¨x = ζ

cosθ− ζ

sinθtanζ

(39)

(3)

cosθcos

−3ζ

sinθsinζ

cosζ

cos

−

cosθ−ζ

cosθcos

sinθ

cos

(40)

˙y = ζ

sinθ (41)

¨y = ζ

sinθ+ ζ

cosθtanζ

(42)

(3)

sinθcos

+3ζ

cosθsinζ

cosζ

cos

−

sinθ−ζ

sinθcos

−v

cosθ

cos

. (43)

These expressions allow to calculate e

, ˙e

, ¨e

, e

, ˙e

and ¨e

using the reference trajectory (scaled with t)

and the states of the closed loop system. Plugging in

these expressions into (31) and (32), and using (30)

one gets





cosθ −

sinθ

cos

sinθ

cosθ

cos











−A

−B



(44)

with









−3ζ

sinθsinζ

cosζ

−ζ

cosθ+ζ

cosθcos

cos

3ζ

cosθsinζ

cosζ

−ζ

sinθ+ζ

sinθcos

cos





(45)

where the inverse of the coefﬁcient matrix can be cal-

culated symbolically. One obtains





cosθ sinθ

−sinθcos

cosθcos



−A

−B



. (46)

The tracking feedback law is deﬁned by (33)-(34),

(35)-(37), and by (46). A singularity occurs if ζ

= 0 which corresponds to zero longitudinal veloc-

ity. Another singular situation corresponds to ζ

ϕ = u

= ±π/2 which may occur if the steered wheels

are perpendicular to the longitudinal axis of the car.

Singularities imply the loss of controllability of the

kinematic car model.

6.2 Linearized Error Dynamics

The above method needed the time derivatives of the

velocity to carry out the time-scaling which may be

difﬁcult to measure or estimate in real application.

The method presented in this section uses a transfor-

mation of the tracking error expressed in the conﬁg-

uration variables, and the non-linear model obtained

is linearized around the reference trajectory. The lin-

earized model is controlled by a state feedback similar

to the one reported in (Dixon et al., 2001). The lost

input, which is the longitudinal velocity of the WMR

is again replaced by a virtual input which depends on

the time-scaling of the reference trajectory.

A slightly different kinematic model is used for

this method such that the longitudinal velocity of the

rear axle midpoint and the tangent of the steering an-

gle (u

= tanϕ) are the inputs of the mobile robot. If

the one input case is considered, u

= tanϕ is the sin-

gle control input.

Suppose, that the desired behavior of the robot

is given by the time functions x

τ,ref

(τ), y

τ,ref

(τ),

τ,ref

(τ) such that these functions identically sat-

isfy (7)-(9) for the corresponding reference input sig-

nals u

τ,1,ref

and u

τ,3,ref

= tanu

τ,2,ref

We suggest to scale this reference trajectory ac-

cording to the time t. The scaled reference trajectory

is given by x

ref

(t) = x

τ,ref

(τ), y

ref

(t) = y

τ,ref

(τ), and

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

ref

(t) = θ

τ,ref

(τ) and similarly to (7)-(9)

′

τ,ref

= u

τ,1,ref

cosθ

τ,ref

(47)

′

τ,ref

= u

τ,1,ref

sinθ

τ,ref

(48)

′

τ,ref

= u

τ,1,ref

τ,3,ref

. (49)

The tracking errors are deﬁned for the conﬁguration

variables as e

= x− x

ref

, e

= y− y

ref

, and e

= θ−

ref

. Let us now consider the transformation













cosθ sinθ 0

−sinθ cosθ 0

0 0 1













(50)

of the error vector (e

) to a frame ﬁxed to the

car such that the longitudinal axis of the car coincides

the transformed x axis. Differentiating this equation

w.r.t. time t and using the general rule ˙a(τ) =

da(τ)

∂a

∂τ

∂t

= a

′

τ we get the differential equation





˙e









0 v

car

−v

car

0 0

0 0 0

















sine





τ,1,ref

τ+





0 0

0 w





(51)

which describes the evolution of the errors with re-

spect to the reference path. The inputs w

and w

are

= v

car

−

τu

τ,1,ref

cose

(52)

= v

car

−

τu

τ,1,ref

τ,3,ref

. (53)

Notice that from these inputs w

and w

the ﬁrst

derivative of the time scaling (

τ) and the real input

= tanϕ can be calculated as

τ =

car

− w

τ,1,ref

cose

(54)

τu

τ,1,ref

τ,3,ref

car

(55)

if the reference value for the longitudinal velocity

τ,1,ref

6= 0, the error of the orientation e

6= ±π/2,

and the longitudinal velocity of the car v

car

6= 0.

This system can be linearized along the refer-

ence trajectory, i.e. for [

]

= 0. The

linearized system is controllable if at least one of

the reference control inputs (u

τ,1,ref

τ,3,ref

) is non-

zero. The setpoint of the linearized system obtained

from (51) can be locally stabilized by a state feedback

of the form





= −K









(56)

0 5 10 15 20

0.5

1.5

2.5

time t

velocity [m/s]

Longitudinal velocity profiles

reference

quick driver

slow driver

traveling time of the quick driver

traveling time

of the slow driver

Figure 3: Velocity proﬁles for the reference, for the quick

driver, and for the slow driver. The traveling times are ob-

tained in closed loop.

such that the gain matrix K puts the eigenvalues of

the closed loop system in the left half of the complex

plane.

The way of calculations is as follows. One sup-

pose that the tracking errors of the conﬁguration vari-

ables (e

) are measured, hence the the error

) can be determined using (50). Then the

state feedback (56) allows to calculate w

and w

From the actual value of w

one can determine

τ using

the current value of v

car

, e

, and the value of u

τ,1,ref

according to the time t obtained by scaling the ref-

erence. The input u

= tanϕ is calculated according

to (55) using w

. The function τ(t) is obtained by the

on-line integration of

τ determined by (54) using the

initial condition τ(0) = 0. The time distribution of the

reference trajectory is ﬁnally modiﬁed according to τ

and

τ.

Since a linearized model was used for the con-

troller design only local stability is guaranteed. (E.g.

if w

≈ 0 is not fulﬁlled,

τ in (54) can get a negative

value, which is not allowed since time cannot rewind.)

7 SIMULATIONS

Examples are shown to demonstrate the functioning

of both time-scaling based tracking controllers for the

one input case.

7.1 Results of Flatness-Based Solution

We use the feedback described in Subsection 6.1, such

that u

τ,1

generated by the feedback law drives the

time-scaling given in Section 5 together with the mea-

sured v

car

and its two successive time derivatives. The

reference trajectory starts from the point (x

τ,ref

(0) =

0,y

τ,ref

(0) = 0,θ

τ,ref

(0) = 0) and arrives to the point

τ,ref

(T) = 10, y

τ,ref

(T) = 3.5, θ

τ,ref

(T) = 0), all

TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A SINGLE STEERING INPUT - Control Using

Reference Time-Scaling

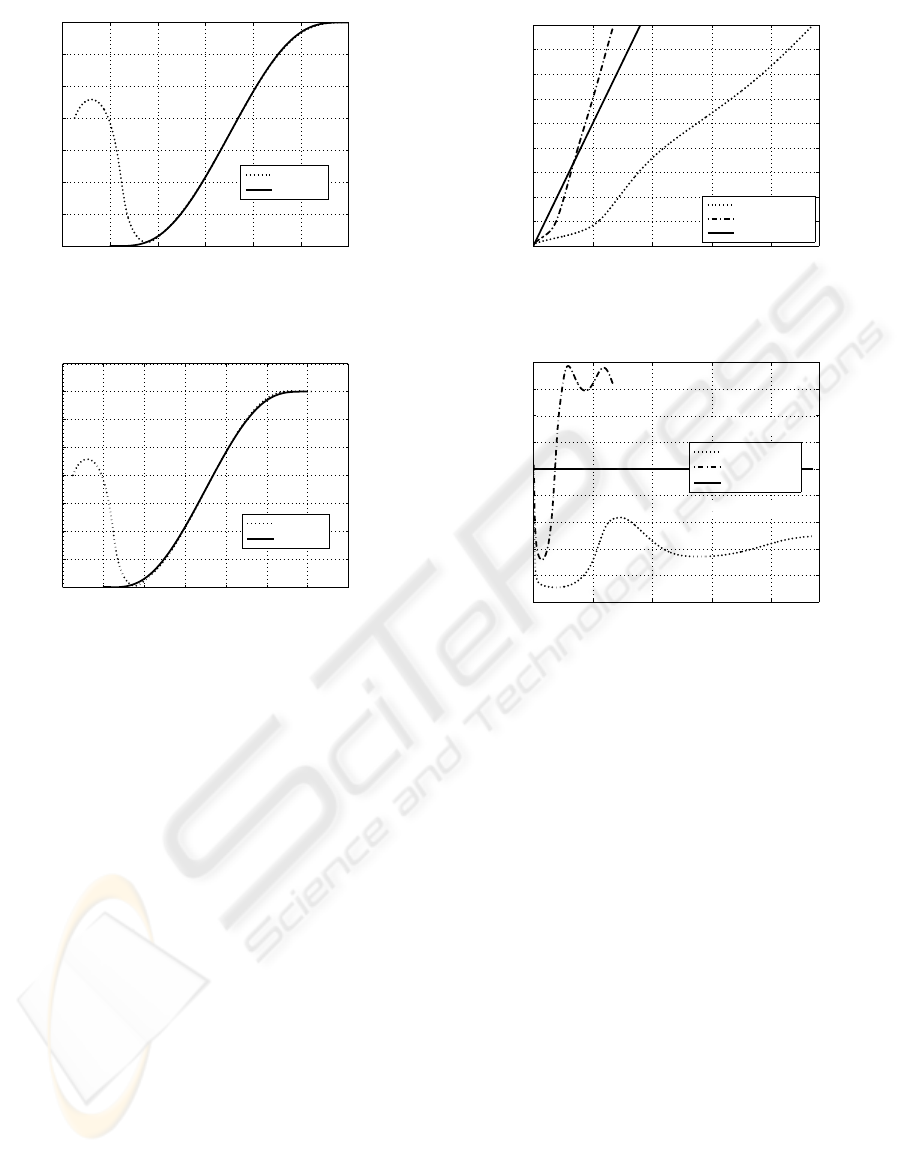
−2 0 2 4 6 8 10

0.5

1.5

2.5

3.5

Real and reference trajectories

Real

Reference

Figure 4: Real and reference trajectories in the horizontal

plane – slow driver.

−2 0 2 4 6 8 10 12

0.5

1.5

2.5

3.5

Real and reference trajectories

Real

Reference

Figure 5: Real and reference trajectories in the horizontal

plane – quick driver.

distances are given in meters and the orientation is

given in radians. The traveling time of the reference

trajectory is T = 9 seconds.

The real initial conﬁguration of the WMR differs

from the one used for motion planning, since x(0) =

−1.5, y(0) = 2, and θ(0) = π/4.

Two cases are presented such that the geometry

of the reference trajectory and the reference velocity

proﬁle obtained are the same. The driver’s behavior is

different for the two cases. In the ﬁrst case, referred

to as the slow driver case, the driver imposes con-

siderably slower velocities than those obtained by the

motion planning. In the second case, referred to as the

quick driver case, the driver generates higher veloci-

ties than the reference velocity proﬁle. All velocity

proﬁles are given in Figure 3.

The geometries of the reference trajectories and

the real trajectories in the horizontal plane are de-

picted in Figure 4 (slow driver) and in Figure 5 (quick

driver). Exponential tracking of the reference trajec-

tory is achieved for each scenario with similar geom-

etry of the real path. Figure 6 and Figure 7 show the

effects of on-line time-scaling. If the car is driven by

a slow driver it needed more than 23 seconds accord-

0 5 10 15 20

time t

time τ

Time scaling functions τ(t)

slow driver

quick driver

without scaling

Figure 6: The time-scaling functions τ(t) along the path for

the slow and quick drivers.

0 5 10 15 20

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

time t

Derivative of τ(t)

slow driver

quick driver

without scaling

acceleration of the reference

deceleration of the reference

Figure 7: The derivative of the time-scaling functions

τ.

ing to time t to achieve the traveling time T = 9 sec

which is given for the reference trajectory according

to the time τ. The reference in τ was decelerated all

along the trajectory (

τ < 1). The deceleration is also

accentuated at low values of t which corresponds to

large tracking errors. The time-scaling is completely

different for the quick driver who reaches the end of

the trajectory faster according to the time t than ac-

cording to the time τ which means that the reference

was accelerated except a short section at the begin-

ning where the tracking error elimination slows down

the time-scaling despite the driver’s efforts.

7.2 Results Obtained by State Feedback

Here we use the feedback law described in the sub-

section 6.2 such that the same reference trajectory and

initial conﬁguration were used as in the previous sub-

section.

The reference trajectory and the real path are

shown in Figure 8 for the velocity proﬁles depicted

in Figure 9. We achieved exponential tracking.

If the difference between the real and reference

initial conﬁgurations is larger, the linearized model is

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

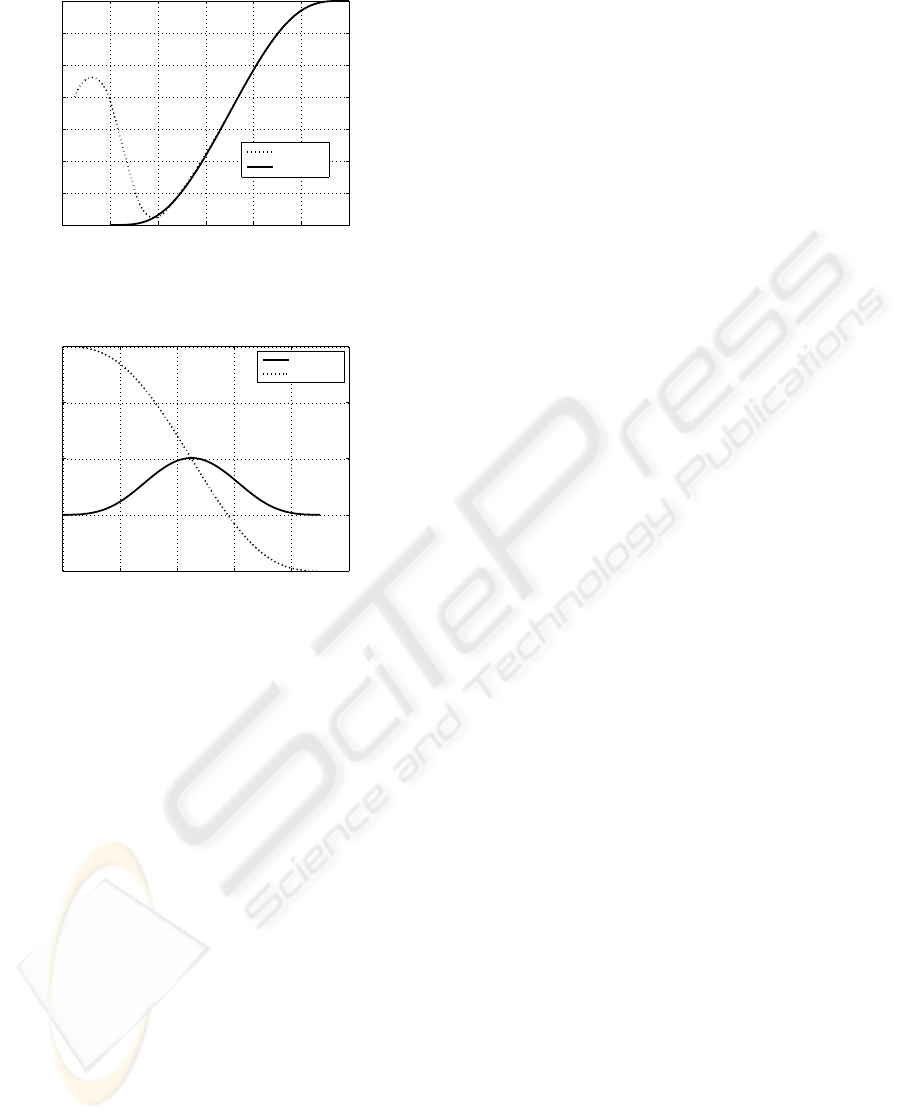
−2 0 2 4 6 8 10

0.5

1.5

2.5

3.5

Real and reference trajectories

Real

Reference

Figure 8: Real and reference trajectories in the horizontal

plane – simulation 1.

0 2 4 6 8 10

0.5

1.5

2.5

time t

velocity [m/s]

Longitudinal velocity profiles

Reference

Real

Figure 9: Velocity proﬁles for the reference and for the car

in simulation 1.

no longer valid and the time-scaling may rewind.

8 CONCLUSION

The paper presented two time-scaling based tracking

control methods for WMRs with one input such that

the longitudinal velocity of the vehicle is generated

externally and cannot be considered as a control in-

put. The time-scaling involves the car velocity and its

derivatives which need to be measured or estimated.

For the tracking controller designed for the linearized

error dynamics the time derivatives of the velocity are

not needed. The exponential decay of the initial error

along the trajectory can be ensured. The results can

be extended for the n-trailer case.

ACKNOWLEDGEMENTS

The research was partially supported by the Hun-

garian Science Research Fund under grant OTKA T

068686 and by the Advanced Vehicles and Vehicle

Control Knowledge Center under grant RET 04/2004.

REFERENCES

Benalia, A., Djemai, M., and Barbot, J.-P. (2003). Control

of the kinematic car using trajectory generation and

the high order sliding mode control. In Proceedings of

the IEEE International Conference on Systems, Man,

and Cybernetics, volume 3, pages 2455–2460.

Cuesta, F. and Ollero, A. (2005). Intelligent Mobile Robot

Navigation, volume 16 of Springer Tracts in Ad-

vanced Robotics. Springer, Heidelberg.

Dahl, O. and Nielsen, L. (1990). Torque-Limited Path Fol-

lowing by On-Line Trajectory Time Scaling. IEEE

Trans. Robot. Automat., 6(5):554–561.

Dixon, W. E., Dawson, D. M., Zergeroglu, E., and Be-

hal, A. (2001). Nonlinear Control of Wheeled Mobile

Robots. In Lecture Notes in Control and Information

Sciences. Springer.

Fliess, M., L

evine, J., Martin, P., and Rouchon, P. (1995).

Flatness and Defect of Nonlinear Systems: Intro-

ductory Theory and Examples. Int. J. of Control,

61(6):1327–1361.

Fliess, M., L

evine, J., Martin, P., and Rouchon, P. (1999). A

Lie-B

acklund Approach to Equivalence and Flatness

of Nonlinear Systems. IEEE Trans. Automat. Contr.,

44(5):922–937.

Fraichard, T. and Scheuer, A. (2004). From Reeds and

Shepps to Continuous-Curvature paths. IEEE Trans-

action on Robotics and Automation, 20.

Gu, D. and Hu, H. (2002). Neural Predictive Control for

a Car-like Mobile Robot. Robotics and Autonomous

Systems, 39:73–86.

Guay, M. (1999). An Algorithm for Orbital Feedback

Llinearization of Single-Input Control Afﬁne Sys-

tems. Systems and Control Letters, 38:271–281.

Hollerbach, J. M. (1984). Dynamic Scaling of Manipula-

tor Trajectories. Trans. of the ASME, J. of Dynamic

Systems, Measurement, and Control, 106(1):102–106.

evine, J. (2004). On the Synchronization of a Pair of Inde-

pendent Windshield Wipers. IEEE Trans. Contr. Syst.

Technol., 12(5):787–795.

Respondek, W. (1998). Orbital Feedback Linerization of

Single-Input Nonlinear Control Systems. In Proceed-

ings of the IFAC NOLCOS’98, pages 499–504, En-

schede, The Netherlands.

Rouchon, P., Fliess, M., L

evine, J., and Martin, P. (1993).

Flatness and Motion Planning: The Car with n-

Trailers. In ECC’93, Proceedings of the European

Control Conference, pages 1518–1522.

Sampei, M. and Furuta, K. (1986). On Time Scaling

for Nonlinear Systems: Application to Lineariza-

tion. IEEE Transactions on Automatic Control, AC-

31:459–462.

adeczky-Kardoss, E. and Kiss, B. (2006). Tracking Er-

ror Based On-Line Trajectory Time Scaling. In INES

2006, Proc. of 10th Int. Conf. on Intelligent Engineer-

ing Systems, pages 80–85.

TRACKING CONTROL OF WHEELED MOBILE ROBOTS WITH A SINGLE STEERING INPUT - Control Using

Reference Time-Scaling