ROBUST AND ACTIVE TRAJECTORY TRACKING FOR AN
AUTONOMOUS HELICOPTER UNDER WIND GUST
Adnan Martini, Franc¸ois L
´
eonard and Gabriel Abba
Industrial Engineering and Mechanical Production Lab (LGIPM), ENIM, Ile du Saulcy, 57045 Metz cedex 1, France
Keywords:
Helicopter, Nonlinear systems, Robust nonlinear control, Active disturbance rejection control, Observer.
Abstract:
The helicopter manoeuvres naturally in an environment where the execution of the task can easily be affected
by atmospheric turbulences, which lead to variations of its model parameters.The originality of this work
relies on the nature of the disturbances acting on the helicopter and the way to compensate them. Here, a
nonlinear simple model with 3-DOF of a helicopter with unknown disturbances is used. Two approaches of
robust control are compared via simulations: a nonlinear feedback and an active disturbance rejection control
based on a nonlinear extended state observer(ADRC).
1 INTRODUCTION
The control of nonlinear systems under disturbance is
an active sector of research in the last decades espe-
cially in aeronautics where several elegant approaches
were presented. We consider here the problem of con-
trol of a Lagrangian model with 3- DOF of a heli-
copter assembled on a platform (VARIO 23cc). It is
subjected to a wind gust and it carries out a vertical
flight (takeoff, slope, flight, descent and landing). The
mathematical model of the system is very simple but
its dynamic is not trivial (nonlinear in state, and un-
deractuated).
Basically, the methods of control which adress
the attenuation of the disturbance, can be classified
according to the different kinds of disturbances. A
possible approach is to model the disturbances by a
stochastic process, which leads to the theory of non-
linear stochastic control (Gokc¸ek et al., 2000). An-
other approach is the nonlinear control (Marten et al.,
2005) where it is supposed that the energy of the dis-
turbances is limited. A third approach is to treat the
disturbances produced by a neutral stable exogenous
system using the nonlinear theory of output regula-
tion (Isidori, 1995) (Byrnes et al., 1997) and (Marconi
and Isidori, 2000). (Wei, 2001) showed the control
of the nonlinear systems with unknown disturbances,
where an approach based on the disturbance observer
based control (DOBC) is carried out: a nonlinear ob-
server of disturbance is presented to estimate the un-
known disturbances. This is integrated with a con-
ventional controller by using techniques based on the
observation of the disturbance. (Hou et al., 2001) pro-
posed a method of active disturbance rejection control
(ADRC) which estimates the disturbance with an ex-
tended state observer. Many industrial applications
use this method (Gao et al., 2001) (Zeller et al., 2001)
(Jiang and Gao, 2001) and (Hamdan and Gao, 2000).
In this paper, an observer methodology is pro-
posed to control a disturbed drone helicopter. It is
based on the concept of active disturbance rejection
control (ADRC). In this approach the disturbances are
estimated by using an extended state observer (ESO)
and are compensated for each sampling period.
In section 2, a model of a disturbed helicopter is
presented. Details of the section of ADRC control are
given in section 3. Section 4 presents an application
of this method on our problem. Section 5 is dedicated
to the zero-dynamics analysis. In section 6, several
simulations of the helicopter under wind gust show
the relevance of the two controls which are described
in this work.
333
Martini A., Léonard F. and Abba G. (2007).
ROBUST AND ACTIVE TRAJECTORY TRACKING FOR AN AUTONOMOUS HELICOPTER UNDER WIND GUST.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 333-340
DOI: 10.5220/0001644403330340
Copyright
c
 SciTePress

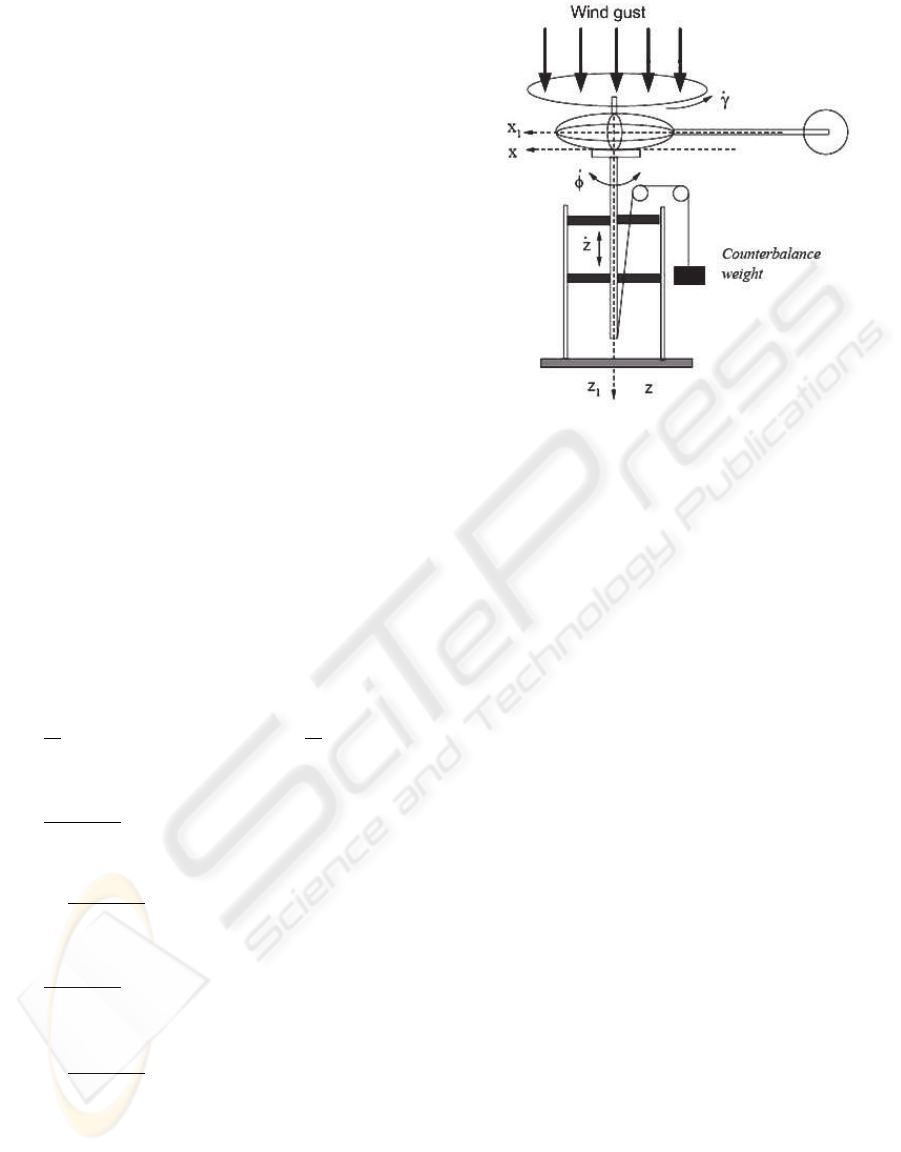
2 MODEL OF THE DISTURBED
HELICOPTER
This section presents the nonlinear model of the
disturbed helicopter (Martini et al., 2005) starting
from a non disturbed model (Vilchis et al., 2003).
The Lagrange equation, which describes the system
of the helicopter-platform with the disturbance (see
figure1), is given by:
M(q)¨q + C(q, ˙q) + G(q) = Q(q, ˙q, u, v
raf
) (1)
The input vector of the control and the state
vector are respectively u =
[u
1
u
2
]
T
,
x = [z ˙z φ
˙
φ γ ˙γ]
T
. The in-
duced gust velocity is noted v
raf
.
Moreover, q =
[z φ γ]
T
,where z repre-
sents the helicopter altitude, φ is the yaw angle
and γ represents the main rotor azimuth angle,
M ∈ R
3×3
is the inertia matrix, C ∈ R
3×3
is the Coriolis and centrifugal forces matrix,
G ∈ R
3
represents the vector of conservative forces,
Q(q, ˙q, u, v
raf
) =
[f
z
τ
z
τ
γ
]
T
is the vector
of generalized forces. The variables f
z
, τ
z
and τ
γ
represent respectively, the vertical force, the yaw
torque and the main rotor torque. Finally, the rep-
resentation of the reduced system of the helicopter,
which is subjected to a wind gust, can be written in
the following state form (Martini et al., 2005):
˙x
1
=x
2
= ˙z
˙x
2
=
1
c
0
[c
8
˙γ
2
u
1
+ c
9
˙γ + c
10
− c
7
] +
1
c
0
c
16
˙γv
raf
˙x
3
=x
4
=
˙
φ
˙x
4
=
1
c
1
c
5
− c
2
4
[c
5
c
11
˙γ
2
u
2
− c
4
((c
12
˙γ + c
13
+
c
8
˙γv
raf
)u
1
+ c
14
˙γ
2
+ c
15
)]
−
c
4
c
1
c
5
− c
2
4
[2c
9
v
raf
+ c
17
v
2
raf
] =
¨
φ
˙x
5
=x
6
= ˙γ
˙x
6
=
1
c
1
c
5
− c
2
4
[c
11
c
4
˙γ
2
u
2
+ c
1
c
4
((c
12
˙γ + c
13
c
8
˙γv
raf
)u
1
+ c
14
˙γ
2
+ c
15
)]
+
1
c
1
c
5
− c
2
4
[2c
9
v
raf
+ c
17
v
2
raf
] = ¨γ
(2)
where c
i
(i =0,...,17) are the physical constants of the
model.
Figure 1: Helicopter-platform (Vilchis et al., 2003).
3 NONLINEAR EXTENDED
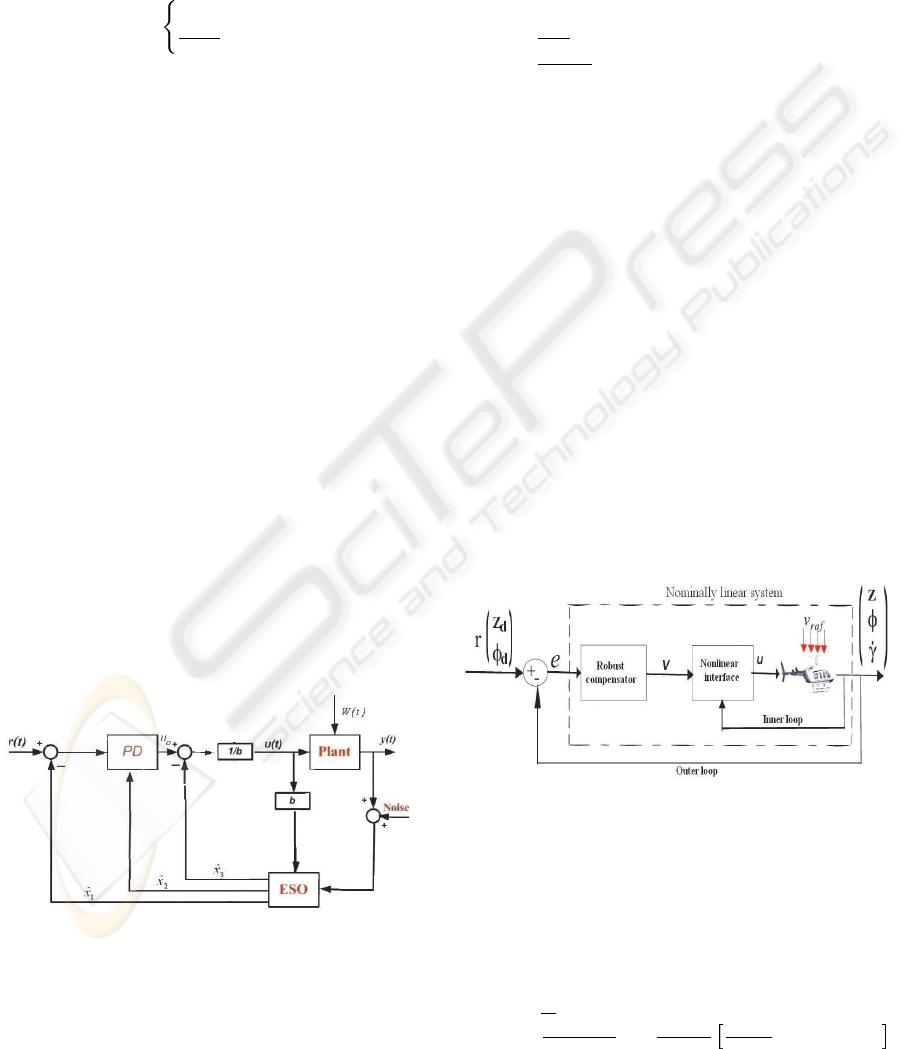
STATE OBSERVER (NESO)
The primary reason to use the control in closed loop
is that it can treat the variations and uncertainties
of model dynamics and the outside unknown forces
which exert influences on the behavior of the model.
In this work, a methodology of generic design is pro-
posed to treat the combination of two quantities, de-
noted as disturbance.
A second order system described by the following
equation is considered (Gao et al., 2001)(Hou et al.,
2001):
¨y = f(y, ˙y, w) + bu (3)
where f(.) represents the dynamics of the model and
the disturbance, w is the input of unknown distur-
bance, u is the input of control, and y is the measured
output. It is assumed that the value of the parameter b
is given. Here f(.) is a nonlinear function.
An alternative method is presented by (Han,
1999)(Han, 1995) as follows. The system in (3) is
initially increased:



˙x
1
= x
2
˙x
2
= x
3
+ bu
˙x
3
=
˙
f
(4)
where x
1
= y, x
2
= ˙y, x
3
= f (y, ˙y, w). f(.) is
treated as an increased state. Here f and
˙
f are un-
known. By considering f(y, ˙y, w) as a state, it can be
estimated with a state estimator. Han in (Han, 1999)
proposed a nonlinear observer for (4):
˙
ˆx = Aˆx + Bu + Lg(e, α, δ)
ˆy = C ˆx
(5)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
334

where:
A =


0 1 0
0 0 1
0 0 0


, B =


0
b
0


, C =

1 0 0

(6)
and L =

L
1
L
2
L
3

. The observer error is
e = y − ˆx
1
and:
g
i
(e, α
i
, δ)
|i=1,2,3
=
|e|
α
i
sign(e) |e| > δ
e
δ
1−α
i
|e| ≤ δ
δ > 0
The observer is reduced to the following set of
state equations, and is called extended state observer
(ESO):



˙
ˆx
1
= ˆx
2
+ L
1
g
1
(e, α, δ)
˙
ˆx
2
= ˆx
3
+ L
2
g
2
(e, α, δ) + bu
˙
ˆx
3
= L
3
g
3
(e, α, δ)
(7)
The active disturbance rejection control (ADRC) is
then defined as a method of control where the value
of f(y, ˙y, w) is estimated in real time and is compen-
sated by the control signal u. Since ˆx
3
→ f , it is used
to cancel actively f by the application of:
u = (u
0
− ˆx
3
)/b (8)
This expression reduces the system to:
¨y = (f − ˆx
3
) + u
0
≈ u
0
(9)
The process is now a double integrator with a unity
gain, which can be controlled with a PD controller:
u
0
= k
p
(r − ˆx
1
) − k
d
ˆx
2
(10)
where r is the reference input. The observer gains L
i
and the controller gains k
p
and k
d
can be calculated
by a pole placement. The configuration of ADRC is
presented in figure2 :
Figure 2: ADRC structure.
4 CONTROL OF DISTURBED
HELICOPTER
4.1 Control by Nonlinear Feedback
Firstly, the nonlinear terms of the non disturbed model
(v
raf
= 0 ) are compensated by introducing two new
controls V
1
and V
2
such as(see Fig.3):
u
1
=
1
c
8
˙γ
2
[c
0
V
1
− c
9
˙γ − c
1
0 + c
7
]
u
2
=
1
c
5
c
11
˙γ
2
[(c
1
c
5
− c
2
4
)V
2
+ c
4
((c
12
˙γ+
c
13
)u
1
+ c
14
˙γ
2
+ c
15
)].
(11)
By using the above controls V
1
and V
2
, for v
raf
= 0,
an uncoupled linear system is obtained which is rep-
resented by two equations: ¨z = V
1
,
¨
φ = V
2
. Stabi-
lization is carried out by a pole placement. To regu-
late altitude z and the yaw angle φ, a PID controller is
proposed:
V
1
= −a
1
˙z − a
2
(z − z
d
) − a
3
R
t
0
(z − z
d
)dt
V
2
= −a
4
˙
φ − a
5
(φ − φ
d
) − a
6
R
t
0
(φ − φ
d
)dt
(12)
where z
d
and φ
d
are the desired trajectories. The
parameters of regulation were calculated using two
dominant poles in closed loop such as:
z

ω
z
= 2rad/s
ξ
z
= 1
and φ

ω
φ
= 5rad/s
ξ
φ
= 1
(13)
where ω
z
, ω
φ
are the natural frequencies, and ξ
z,φ
are the damping ratios for the pole placement. These
integral controllers are used to eliminate the effect of
low frequency disturbance.
Figure 3: Architecture of nonlinear feedback control.
4.2 Active Disturbance Rejection
Control (ADRC)
Since v
raf
6= 0 , a nonlinear system of equations is
obtained:
¨z = V
1
+
1
c
0
c
16
˙γv
raf
¨
φ = V
2
−
c
4
c
0
v
raf
(c
1
c
5
−c
2
4
) ˙γ
V
1
−
c
4
v
raf
c
1
c
5
−c
2
4
c
7
−c
10
˙γ
+ c
9
+ c
17
v
raf
(14)
ROBUST AND ACTIVE TRAJECTORY TRACKING FOR AN AUTONOMOUS HELICOPTER UNDER WIND GUST
335

The stabilization is always done by pole placement.
To regulate altitude z and the yaw angle φ , we can
notice that (14) represent two second order systems
which can be written as in (3):
¨y = f(y, ˙y, w) + bu (15)
with b = 1,u = V
1
or V
2
and:
f
z
(y, ˙y, w) =
1
c
0
c
16
˙γv
raf
f
φ
(y, ˙y, w) = −
c
4
c
0
v
raf
(c
1
c
5
−c
2
4
) ˙γ
V
1
−
c
4
v
raf
c
1
c
5
−c
2
4
h
c
7
−c
10
˙γ
+
+c
9
+ c
17
v
raf
]
For each control, an observer is built using (7):
• for altitude z :



˙
ˆx
1
= ˆx
2
+ L
1
g
1
(e
z
, α
1
, δ
1
)
˙
ˆx
2
= ˆx
3
+ L
2
g
2
(e
z
, α
2
, δ
2
) + bV
1
˙
ˆx
3
= L
3
g
3
(e
z
, α
3
, δ
3
)
(16)
where e
z
= z − ˆx
1
is the observer error, g
i
(e
i
, α
i
, δ
i
)
is defined as exponential function of modified gain.
g
i
(e
z
, α
iz
, δ
i
)
|i=1,2,3
=
|e
z
|
α
iz
sign(e
z
), |e
z
| > δ
i
e
z
δ
1−α
iz
i
, |e
z
| ≤ δ
i
with 0 < α
i
< 1 and 0 < δ
i
, a PID controller
is used in stead of PD(10) to attenuate the effects of
disturbance:
V
1
= −k
1
ˆx
2
− k
2
(ˆx
1
− z
d
) − k
3
Z
t
0
(ˆx
1
− z
d
)dt − ˆx
3
(17)
The control signal V
1
takes into account the terms
which depend on the observer (ˆx
1
, ˆx
2
) . The fourth
part, which also comes from the observer, is added to
eliminate the effect of disturbance in this system.
• for the yaw angle φ :



˙
ˆx
4
= ˆx
5
+ L
4
g
4
(e
φ
, α
4
, δ
4
)
˙
ˆx
5
= ˆx
6
+ L
5
g
5
(e
φ
, α
5
, δ
5
) + bV
2
˙
ˆx
6
= L
6
g
6
(e
φ
, α
6
, δ
6
)
(18)
where e
φ
= φ − ˆx
4
is the observer error, with
g
i
(e
φ
, α
iφ
, δ
i
) is defined as exponential function of
modified gain:
g
i
(e
φ
, α
iφ
, δ
i
)
|i=4,5,6
=
|e
φ
|
α
iφ
sign(e
φ
), |e
φ
| > δ
i
e
φ
δ
1−α
iφ
i
, |e
φ
| ≤ δ
i
V
2
= −k
5
ˆx
4
−k
4
(ˆx
5
−φ
d
)− k
6
Z
t
0
(ˆx
4
−φ
d
)dt− ˆx
6
(19)
z
d
and φ
d
are the desired trajectories. PID parameters
are designed to obtain two dominant poles in closed-
loop:
forz

ω
c1
= 2rad/s
ξ
1
= 1
and forφ

ω
c2
= 5rad/s
ξ
2
= 1
(20)
5 ZERO DYNAMICS PROBLEM
The zero dynamics of a nonlinear system are its inter-
nal dynamics subject to the constraint that the outputs
(and, therefore, all their derivatives) are set to zero for
all times (Isidori, 1995)(Slotine and Li, 1991). Non-
linear systems with nonasymptotically stable zero-
dynamics are called strictly (or weakly, if the zero
dynamics are marginally stable) nonminimum phase
system. The output of our system is q =

z φ

T
and its control input u =

u
1
u
2

T
. The calcula-
tion of the relative degrees gives: r
1
= r
2
= 2. The
dimension of our model n = 5 so that: r
1
+ r
2
< n
what implies the existence of an internal dynamics.
If a linearizable feedback is used, it is necessary to
check the stability of this internal dynamics. In fact
the ˙γ dynamics represents the zeros-dynamics of (2).
Moreover the nonlinear terms of the non disturbed
model (v
raf
= 0 ) can be compensated by introduc-
ing two new controls V
1
and V
2
. Since v
raf
= 0, a
nonlinear system of equations is then obtained:
¨z = V
1
;
¨
φ = V
2
¨γ =
1
c
1
c
5
−c
2
4
[b
1
V
1
+ b
2
V
2
+ b
3
]
(21)
Where:
b
1
=
c
4
c
0
c
5
c
8
˙γ
2
(c
12
˙γ + c
13
)(c
1
c
5
+ c
4
)
b
2
=
c
4
c
5
(c
1
c
5
− c
2
4
)
b
3
=
c
4
c
5
(c
1
c
5
+ c
4
)[(c
12
˙γ + c
13
)(−c
9
˙γ−
c
10
+ c
7
) ×
1
c
8
˙γ
2
+ c
14
˙γ
2
+ c
15
)]
(22)
Zero dynamics of nondisturbed model can then obvi-
ously be got by putting z = φ = 0 ⇒ ˙z =
˙
φ = 0 ⇒
¨z =
¨
φ = 0 ⇒ V
1
= V
2
= 0:
¨γ =
1
c
1
c
5
− c
2
4
b
3
(23)
Simplified in:
¨γ = b
4
˙γ
2
+
b
5
˙γ
2
+
b
6
˙γ
+ b
7
(24)
With: b
4
= 4.1425 × 10
−5
, b
5
= −778300, b
6
=
−6142 and b
7
= 0.1814. To get possible equilib-
rium points dynamics of (24), the following equation
is solved:
b
4
˙γ
4
+ b
7
˙γ
2
+ b
6
˙γ + b
5
= 0 (25)
The four solutions of (25) are ˙γ
∗
= −219.5 ±
468.2i, 563.71 and −124.6 rad/s. Only the two last
values of ˙γ
∗
have physical meaning for the system.
On the other hand, the value ˙γ
∗
= 563.7rad/s is too
high regarding the blade fragility. As a result, the only
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
336

equilibrium point to consider is ˙γ
∗
= −124.6rad/s.
The ˙γ−dynamics(24), linearized around the equilib-
rium point of interest ˙γ
∗
= −124.634 rad/s, has a
real eigenvalue equal to −0.419. As a consequence,
all trajectories starting sufficiently near ˙γ
∗
converge
to the latter. Then it follows that the zeros-dynamics
of (21) has a stable behavior. Simulation results show
that ˙γ remains bounded away from zero during the
flight. For the chosen trajectories and gains ˙γ con-
verges rapidly to a constant value(see Figure6). This
is an interesting point to note since it shows that the
dynamics and feedback control yield flight conditions
close to the ones of real helicopters which fly with a
constant ˙γ thanks to a local regulation feedback of the
main rotor speed (which does not exist on the VARIO
scale model helicopter).
6 RESULTS IN SIMULATION
To show the efficiency of active disturbance rejection
control (ADRC), it is compared to the nonlinear con-
trol, which uses a PID controller. The various numer-
ical values are the following:
6.1 Control by Nonlinear Feedback
We have a
1
= 24, a
2
= 84, a
3
= 80, a
4
= 60,
a
5
= 525 and a
6
= 1250, the numerical values are
calculating by pole placement as defined in (13).
6.2 Active Disturbance Rejection
Control (ADRC)
• For z:
k
1
= 24, k
2
= 84, k
3
= 80 (the numerical val-
ues are calculating by pole placement as defined
in (20)). Choosing a triple pole located in ω
0z
such as ω
0z
= (3 ∼ 5)ω
c
1
, one can choose
ω
0z
= 10rad/s, α
1
= 0.5, δ
1
= 0.1. Using
pole placement method, the gains of the observer
for the case |e| ≤ δ (i.e linear observer) can be
evaluated:
L
1
δ
1−α
1
1
= 3 ω
0z
L
2
δ
1−α
1
1
= 3 ω
2
0z
L
3
δ
1−α
1
1
= ω
3
0z
(26)
which leads to: L
i
= {9.5, 95, 316}, i ∈ [1, 2, 3]
• For φ:
k
4
= 60, k
5
= 525, k
6
= 1250 and ω
0φ
=
25rad/s, α
2
= 0.5, δ
2
= 0.025. And by the same
method in (26) one can find the observer gains:
L
i
= {11.9, 296.5, 2470}, i ∈ [4, 5, 6]
For the (ADRC) control, one can show that if the
gains of the observer L
i=1,2,3,4,5,6
are too large, the
convergence of ˆx
i=1,2,3,4,5,6
to the following val-
ues (z, ˙z, ¨z, φ,
˙
φ,
¨
φ) is very fast but the robustness
against the noises quickly deteriorated. By choosing
L
i+1
≫ L
i
(i = 1, 2, · · · , 6) , higher order observer
state ˆx
i+1
will converge to the actual value more
quickly than lower order state ˆx
i
. Therefore, the sta-
bility of ADRC system will be guaranteed. δ is the
width of linear area in the nonlinear function ADRC.
It plays an important role to the dynamic performance
of ADRC. The larger δ is, the wider the linear area.
But if δ is too large, the benefit of nonlinear charac-
teristics would be lost. On the other hand, if δ is too
small, then high frequency chattering will happen just
the same as in the sliding mode control. Generally, in
ADRC, δ is set to be approximately 10% of the vari-
ation range of its input signal. α is the exponent of
tracking error. The smaller α is, the faster the track-
ing speed is, but the more calculation time is needed.
In addition, very small α will cause chattering. In re-
ality, selecting α = 0.5 will provide a satisfactory re-
sult. The induced gust velocity operating on the main
rotor is chosen as (G.D.Padfield, 1996):
v
raf
= v
g m
sin

2πV t
L
u

(27)
where V in m/s is the rise speed of the helicopter and
v
g m
= 0.68m/s is the gust density. This density cor-
responds to an average wind gust, and L
u
= 1.5m
is its length (see Figure8). In simulation the gust is
applied at t=80s.
A band limited white noise of covariance 2 ×
10
−8
m
2
for z and 2 × 10
−9
rad
2
for φ, has been added
equally to the measurements of z and φ for the two
controls. The compensation of this noise is done by
using a Butterworth second-order low-pass filter. Its
crossover frequency for z is ω
cz
= 10rad/s and for φ
is ω
cφ
= 25rad/s.
The parameters used for 3DOF standard heli-
copter model are based on a VARIO 23cc small he-
licopter(see figure 1).
Figure4 shows the desired trajectories. Figure7 il-
lustrates the variations of control inputs, where from
initial conditions when k ˙γk increases quickly, the
control output u
1
and u
2
saturates. Nevertheless the
stability of the closed-loop system is not destroyed.
One can observe that ˙γ → −124.6rad/s as ex-
pected from the previous zero dynamics analysis. One
can also notice that the main rotor angular speed is
similar for the two controls as illustrated in Figure6.
ROBUST AND ACTIVE TRAJECTORY TRACKING FOR AN AUTONOMOUS HELICOPTER UNDER WIND GUST
337

The difference between the two controls appears in
Figure5 where the tracking errors are less significant
by using the PID (ADRC) control than PID controller.
One can see in Figure8 that the main rotor thrust
converges to values that compensate the helicopter
weight, the drag force and the effect of the disturbance
on the helicopter.
The simulations show that the control by nonlinear
feedback PID (ADRC) is more effective than nonlin-
ear PID controller, i.e. the tracking errors are less
significant by using the first control. But the PID
(ADRC) control is a little more sensitive to noise than
PID controller. Moreover, under the effect of noise,
the second control allows the main rotor thrust T
m
to
be less away from its balance position than the first
control (Figure8). Figure9 represent the effectiveness
of the observer: ˆx
3
and f
z
(y, ˙y, w) , are very close
and also ˆx
6
and f
φ
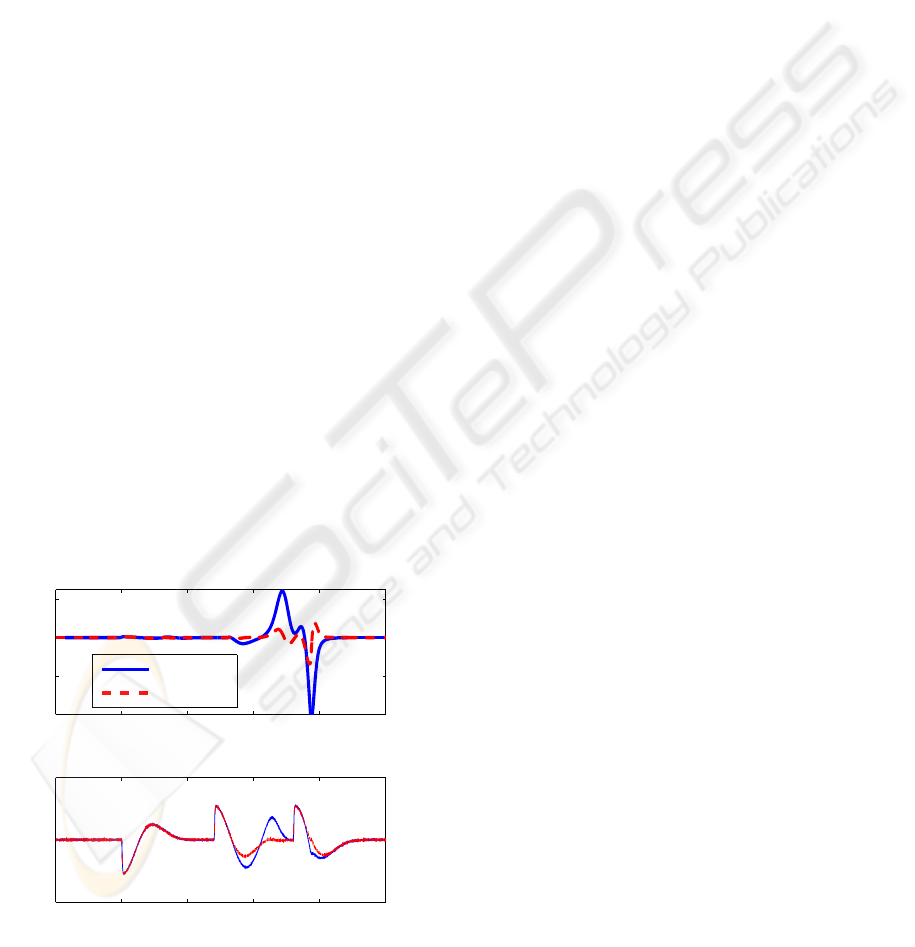
(y, ˙y, w). Observer errors are pre-
sented in the Figure10. By tacking a large disturbance
(v
raf
= 3m/s ), the ADRC control shows a robust
behavior compared to the nonlinear PID control as il-
lustrated in Figure11.
0 50 100 150 200 250
−0.6
−0.4
−0.2
Desired altitude z(m)
0 50 100 150 200 250
−1
0
1
Time(s)
Desired yaw angle φ(rad)
Figure 4: The desired trajectories in z and φ.
7 CONCLUSION
In this paper, the active disturbance rejection control
(ADRC) has been applied to the drone helicopter con-
trol. The basis of ADRC is the extended state ob-
server. The state estimation and compensation of the
change of helicopter parameters and disturbance vari-
ations are implemented by ESO and NESO. By using
0 50 100 150 200 250
−4
−2
0
2
x 10
−3
Altitude error(m)
0 50 100 150 200 250
−2
0
2
x 10
−4
Time(s)
Yaw angle error(rad)
PID
PID(ADRC)
Figure 5: Tracking error in z and φ.
0 50 100 150 200 250
−150
−140
−130
−120
−110
−100
Time(s)
Main rotor speed ˙γ(rad/s)
Figure 6: Variations of the main rotor angular speed ˙γ.
ESO, the complete decoupling of the helicopter is ob-
tained. The major advantage of the proposed method
is that the closed loop characteristics of the heli-
copter system do not depend on the exact mathemati-
cal model of the system. Comparisons were made in
detail between ADRC and conventional nonlinear PID
controller. It is concluded that the proposed control
algorithm produces better dynamic performance than
the nonlinear PID controller. Even for large distur-
bance v
raf
= 3m/s(figure11), the proposed ADRC
control system is robust against the modeling uncer-
tainty and the external disturbance in various operat-
ing conditions. It is indicated that such scheme can
be applicable to aeronautical applications where high
dynamic performance is required. We note that the
next step will be the validation of this study on the
real helicopter model VARIO 23cc.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
338

0 50 100 150 200 250
−6
−4
x 10
−5
Control input u
1
(m)
0 50 100 150 200 250
−2
−1
0
1
x 10
−4
Time(s)
Control input u
2
(m)
PID
PID(ADRC)
Figure 7: The control inputs u
1
and u
2
.
0 50 100 150 200 250
−0.5
0
0.5
Induced gust velocity v
raf
(m/s)
0 50 100 150 200 250
−73.7
−73.6
−73.5
Time(s)
Thrust T
m
(N)
PID(ADRC)
PID
Figure 8: The induced gust velocity v
raf
and the variations
of the main rotor thrust T
M
.
REFERENCES
Byrnes, C., Priscoli, F., Isidori, A., and Kang, W. (1997).
Structurally stable output regulation of nonlinear sys-
tems. Automatica, 33(2):369–385.
Gao, Z., Hu, S., and Jiang, F. (2001). A novel motion
control design approach based on active disturbance
rejection. pages 4877–4882. Orlando, Florida USA,
Proceedings of the 40th IEEE Conference on Decision
and Control.
G.D.Padfield (1996). Helicopter Flight Dynamics: The
Theory and Application of Flying Qualities and Simu-
lation Modeling. Blackwell Science LTD.
0 50 100 150 200 250
−1
0
1
2
f
z
(y, ˙y, w)
ˆx
3
0 50 100 150 200 250
−0.2
0
0.2
Time(s)
f
φ
(y, ˙y, w)
ˆx
6
Figure 9: Estimation of f
z
and f
φ
.
0 50 100 150 200 250
−1
0
1
2
x 10
−3
Altitude observer error(m)
0 50 100 150 200 250
−2
0
2
x 10
−5
Time(s)
Yaw angle observer error (rad)
Figure 10: Observer error in z and φ.
Gokc¸ek, C., Kabamba, P., and Meerkov, S. (2000). Dis-
turbance rejection in control systems with saturating
actuators. Nonlinear Analysis, 40:213–226.
Hamdan, M. and Gao, Z. (2000). A novel pid controller for
pneumatic proportional valves with hysteresis. IEEE
Industrial Application Society 2000 Annual Meeting
and World Conference on Industrial Applications of
Electrical Energy, 2:1198 – 1201.
Han, J. (1995). A class of extended state observers for un-
certain systems. Control and Decision, 10(1):85–88.
Han, J. (1999). Nonlinear design methods for control sys-
tems. Beijing, China, The Proc of the 14th IFAC
World Congress.
ROBUST AND ACTIVE TRAJECTORY TRACKING FOR AN AUTONOMOUS HELICOPTER UNDER WIND GUST
339

Hou, Y., Z. Gao, F. J., and Boulter, B. (2001). Active dis-
turbance rejection control for web tension regulation.
Proceedings of the 40th IEEE Conference on Deci-
sion and Control, Orlando, Florida USA, pages 4974–
4979.
Isidori, A. (1995). Nonlinear Control Systems. Springer-
Verlag, Berlin, 3rd edition edition.
Jiang, F. and Gao, Z. (2001). An application of nonlinear
pid control to a class of truck abs problems. IEEE
Conference on Decision and Control.Orlando, FL,
USA, 1:516–521.
Marconi, L. and Isidori, A. (2000). Robust global stabi-
lization of a class of uncertain feedforward nonlinear
systems. Systems and Control Letters, 41:281–290.
Marten, M., Ludwick, S., and Trumper, D. (2005). A loop
shaping perspective for tuning controllers with adap-
tive feedforward cancellation. Precision Engineering,
29:27 –40.
Martini, A., L
´
eonard, F., and Abba, G. (2005). Suivi
de trajectoire d’un h
´
elicopt
`
ere drone sous rafale de
vent[in french]. CFM 17
`
eme Congr
`
es Franc¸ais de
M
´
ecanique. Troyes, France, CD ROM.N
0
.467.
Slotine, J. and Li, W. (1991). Applied nonlinear control.
Prentic-Hall, Inc.
Vilchis, A., Brogliato, B., Dzul, L., and Lozano, R. (2003).
Nonlinear modeling and control of helicopters. Auto-
matica, 39:1583 –1596.
Wei, W. (2001). Approximate output regulation of a class of
nonlinear systems. Journal of Process Control, 11:69–
80.
Zeller, J., Zhu, M., T.Stimac, and Gao, Z. (2001). Nonlinear
digital control implementation for a dc-dc power con-
verter. Proc. of 36
th
Intersociety Energy Conversion
Engineering Conference IECE
´
C01, Savannah, Geor-
gia.
0 50 100 150 200 250
−0.04
−0.02
0
0.02
Altitude error(m)
0 50 100 150 200 250
−5
0
5
x 10
−4
Yaw angle error(rad)
Time(s)
PID
PID(ADRC)
Figure 11: Test of a large disturbance v
raf
= 3m/s.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
340