A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE

ROBOTS

Jonathan Rogge and Dirk Aeyels

SYSTeMS Research Group, Ghent University, Ghent, Belgium

Keywords:

Multi-robot systems, coverage, exploration, demining.

Abstract:

The present paper develops a novel strategy for the exploration of an unknown environment with a multi-

robot system. Contrary to most exploration problems, the topographical properties of the space need not be

mapped. The algorithm we propose is inspired by methods used for complete coverage of an area, where all

free space has to be physically covered by all robots. In the present paper it is required that the entire free

space is covered by the sensors of the robots, with a certainty of 100%. This weaker requirement enables us

to scan more space in less time, compared to complete coverage algorithms. Moreover the shape of the robot

formation adjusts itself to situations where obstacles, narrow spaces, etc. have to be passed. Communication

between the robots is restricted to line-of-sight and to a maximum interdistance between robots. A direct

application of the algorithm is mine ﬁeld clearance.

1 INTRODUCTION

The research domain of multi-agent robot systems

can be divided into subdomains according to the task

given to the robot group (Ota, 2006). At present well-

studied subdomains are motion-planning (also called

path-planning), formation-forming, region-sweeping,

and combinations of the foregoing. The problem con-

sidered in the present paper belongs to the discipline

comprising region-sweeping. In this discipline two

different robot tasks are usually considered.

In the ﬁrst task a group of robots receives the order

to explore/map an unknown region. The goal is to ob-

tain a detailed topography of the desired area. A typ-

ical approach to tackle the above problem with mul-

tiple robots assumes unlimited communication (Bur-

gard et al., 2005): since exploration algorithms are

already devised for a single robot it seems straight-

forward to divide the area to be explored into disjunct

regions, each of which is assigned to a single robot.

The robots communicate to each other the area they

have explored so that no part of the free space will be

explored twice unnecessarily. At no point during the

task are the robots trying to form a ﬁxed formation.

Each robot explores a different part of the unknown

region and sends its ﬁndings to a central device which

combines the data received from the robots into one

global map of the area.

Closely related to the exploring/mapping task is

the second task, called complete coverage, where the

robots have to move over all of the free surface in

conﬁguration space. Typical applications are mine

ﬁeld clearance, lawn mowing and snow cleaning. The

coverage problem has been addressed in the litera-

ture both in a deterministic and a probabilistic setting.

In the probabilistic approach the robots are consid-

ered as if they were ﬂuid or gas molecules satisfying

the appropriate physical laws of motion (Kerr et al.,

2004), (Keymeulen and Decuyper, 1994). Just as a

gas by diffusion ﬁlls an entire space, the robots will

cover all free space when time tends to inﬁnity. In

the remainder of the paper we focus on the determin-

istic setting. In this setting the robot group typically

forms (partial) formations to solve the task. Refer-

ence (Choset, 2001) gives a short overview of existing

techniques for multi-robot coverage problems. Dif-

ferent approaches to the coverage problem are found

in (Cort

es et al., 2004), (Kurabayashi et al., 1996),

(Wong and MacDonald, 2004), (Zheng et al., 2005)

(Rekleitis et al., 2004) and (Kong et al., 2006).

Rogge J. and Aeyels D. (2007).

A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE ROBOTS.

In Proceedings of the Four th International Conference on Informatics in Control, Automation and Robotics, pages 76-83

DOI: 10.5220/0001645500760083

 SciTePress

The problem statement of the present paper

does not differ that much from the common explo-

ration/mapping task and the complete coverage prob-

lem, but is rather a combination of both. It is required

that all of the free space is sensed by the robots, but

not necessarily physically covered. However, unlike

the common exploration case, the sensing of the area

does not have as goal to map the topography of the

free space and the location of the obstacles in it. Our

aim is to locate several unknown targets within the

free space. Moreover, similar to the complete cov-

erage setting we demand a 100% certainty that all

free space has been covered by the sensors at the

end of the exploration procedure, implying that all

targets have been found. Since the robots no longer

have to cover all free space physically, the novel al-

gorithm will yield a time gain compared to complete

coverage strategies. The developed algorithm is in-

spired by complete coverage strategies as (Rekleitis

et al., 2004), (Kong et al., 2006). In these strategies

it is assumed that the space to be explored does not

have a maze-like structure with many narrow corri-

dors, but is an open space containing only convex

obstacles sparsely spread throughout. In the present

paper we adopt these assumptions, postponing more

complex geometries to future work. Our algorithm is

presented in Section 2 of the paper. A short compari-

son between the algorithm presented here and that of

(Rekleitis et al., 2004) is given in Section 3.

A speciﬁc application we have in mind is mine

ﬁeld clearance using chemical vapor microsensors

(Gage, 1995). Once a landmine is deployed, the en-

vironment near the mine becomes contaminated with

explosives derived from the charge contained in the

mine. The vapor microsensors are able to detect the

chemical vapor signature of the explosives emanating

from the landmines from a distance. This implies that

complete coverage algorithms may be too restrictive

with respect to the demining problem. Performing the

algorithm of the present paper, with the weaker re-

quirement of sensor coverage, will result in a gain of

time.

The algorithm can also be used in problems where

a robot formation has to cross a terrain containing

sparsely spread obstacles. There is a natural trade-off

between coherence of the formation and avoidance of

the obstacles. The robot group is allowed to split in

order to pass the obstacles, resulting in faster progress

of the group across the terrain. The algorithm ensures

that once the obstacle is passed, the robots regroup.

2 AN ALGORITHM FOR

COMPLETE SENSOR

COVERAGE

2.1 Setting

Consider a population of N identical robots. Each

robot is equipped with two types of sensors. One type

serves as a means to detect the goal targets to be found

in the assigned area, e.g. landmines; the other type is

used to detect and locate other robots and obstacles

in the neighborhood of the robot

. Both sensors have

a maximum detection range s

and s

respectively. It

is assumed that targets which come within the radius

of the corresponding sensor area s

or s

of the robot

are always detected, and that if they are located far-

ther away than the distance s

they are never de-

tected. The robot conﬁguration allows limited com-

munication. First, this is expressed by the maximum

detection range s

as described above. Second, line-

of-sight communication is assumed: two robots can

only sense each other if they are sufﬁciently close to

each other and if there is no obstacle located on the

straight line connecting both robots.

Two robots are called connected to each other

when they sense each other. Every robot is assigned

an index number. The initial state of the robot con-

ﬁguration is such that robot i is connected to robots

i− 1 and i+ 1, ∀i ∈ {2,...,N − 1}. (Robot 1 is only

connected to robot 2 and robot N is only connected

to robot N − 1.) An example of such a conﬁguration

is depicted in Figure 1 for N = 6. The dashed circles

Figure 1: Overlapping sensor areas in a possible robot con-

ﬁguration.

have radius s

and signify the sensed area for goal tar-

gets of each robot. It is assumed that

< s

. (1)

In practice the latter type consists of two distinct mini-

mally interfering IR-sensors: one sensing obstacles and the

other sensing robots. Since this is not relevant for the the-

oretical description of the algorithm, these sensors are con-

sidered as if they are one and the same.

A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE ROBOTS

The lower bound on s

in (1) ensures that the areas

sensed for goal targets of neighboring robots partially

overlap, as illustrated by Figure 1.

In a second step, we impose a preferred formation

on the robot group as follows: each robot keeps a con-

stant distance d < s

with its neighbors and observes

them at preferred angles with respect to its forward

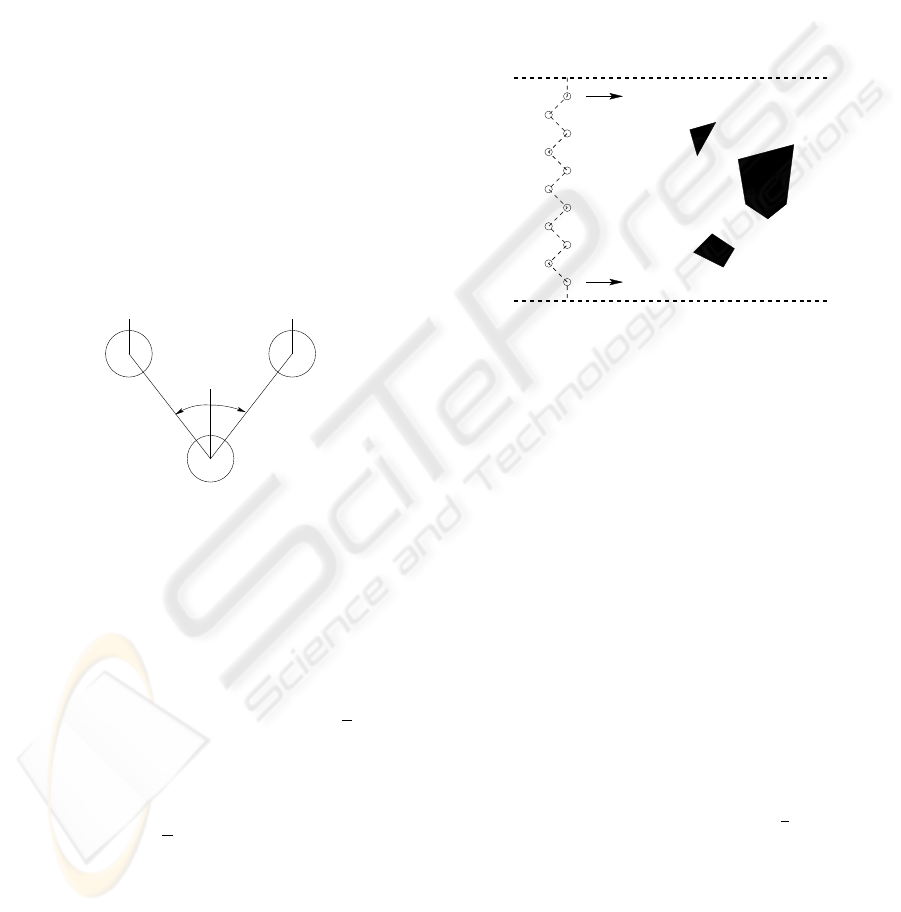
direction. With notation from Figure 2, these angles

are deﬁned by:

(

π/4, i even,

3π/4, i odd,

(

−π/4, i even,

−3π/4, i odd.

(2)

Furthermore each robot is equipped with a compass.

Together with the above deﬁned angles, the forward

direction of each robot (the same for all robots) is im-

posed at the initialization of the algorithm. The above

conditions imply a robot formation with zigzag shape,

as shown in Figure 3. Once the preferred formation is

attained the scanning algorithm is started.

i + 1

i − 1

Figure 2: Deﬁning the angles of the preferred robot conﬁg-

uration.

2.2 The Scanning Algorithm

Assume for simplicity that the area to be explored is

a rectangular subset S of R

. All obstacles contained

in S are assumed disjoint and convex. Divide the set

S into parallel (scanning) strips of width (

− 1)d.

This choice of the value of the width will be motivated

later, in Section 2.4. Furthermore assume that N and d

are such that all obstacles in S have a diameter smaller

than the width of a scanning strip. Fix the maximum

allowed diameter at (

− 3)d. The main idea of the

algorithm is to let the group of robots sweep the area

S strip after strip in a zigzag-like pattern. Clearly,

when there is a sufﬁcient number of robots available

the set S can be regarded as one big strip, simplifying

the algorithm since no transitions between consequent

strips have to be performed.

In a ﬁrst case we consider a strip where no objects

are located on the boundary (see Figure 3). Robots 1

and N are allocated the task to follow the boundaries

of the strip at a constant distance at the constant ve-

locity v. They can be considered leaders of the robot

group. These two leader robots do not try to stay in

the preferred formation, i.e. the condition on the cor-

responding angles α

,β

is removed, and they do not

maintain a ﬁxed interdistance d with their neighbors.

The remaining robots, however, still maintain the pre-

ferred formation. When no obstacles are present in

the strip, the robots scan the strip for goal targets in

the above deﬁned preferred (rigid) formation moving

at a velocity v.

Figure 3: A depiction of the algorithm. The arrows indicate

the constant velocity of both leader robots. The dashed lines

represent the strip boundaries.

When an obstacle is encountered the algorithm

aims to guide the robot group past it in a time-optimal

way. The leader robots start driving at a preset veloc-

ity v

< v (see Section 3); the group is split into two

subgroups in order to move around the obstacle. The

subgroups rejoin after passing the obstacle to resume

the preferred formation structure.

Assume for reasons of simplicity that the number

of robots N is even. Consider the situation where

robot m encounters an object on its path such that

it cannot stay in the preferred formation any longer.

More precisely, the sensors of robot m measure

• an interdistance between the obstacle and the

robot smaller than a preset distance d

< s

• the position of the obstacle at an angle with its

forward direction inside the interval (−γ,γ), with

γ a ﬁxed value inside the interval (0,

The presence of the obstacle is communicated to all

the robots in the group. Each robot takes on a dif-

ferent role such that two subgroups will be formed.

The robots with index i ∈ S

:= {2,...,N/2} now

follow the neighboring robot with corresponding in-

dex i − 1. Similarly, robots with index i ∈ S

{N/2 + 1, . . . , N − 1} follow the neighboring robot

with index i+ 1. More precisely, the robot with in-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Figure 4: A group of 10 robots passing an obstacle. Only robots 5, 6 and 7 apply wall-following around the obstacle during the

maneuver. This is shown in the second and third picture. The ﬁrst picture shows the formation at the moment of encountering

the obstacle. The fourth picture presents the formation after having completely past the obstacle.

dex i tries to reach the following coordinates:

(

i−1

+ dsin

i−1

+ (−1)

dcos

), if i ∈ S

i+1

− dsin

d,y

i+1

+ (−1)

dcos

), if i ∈ S

(3)

These coordinates are considered with respect to a

right-handed (x,y)-frame with the y-axis parallel to

the strip boundary, and directed into the driving di-

rection of the leader robots. Each robot still tries to

stay in the preferred formation, but in order to do so

only takes information of one neighbor into account.

Moreover, the condition on the relative position be-

tween the neighboring robots N/2 and N/2+ 1 is sus-

pended, which will lead to the splitting of the robot

group. Notice that indifferent of the robot that ob-

serves the obstacle ﬁrst, the group will split between

robots N/2 and N/2 + 1. This choice is motivated in

Section 2.4.

Consider the situation for robot i where one of the

following occurs:

• The desired position (3) cannot be reached,

• The obstacle is blocking the straight path between

the present position of robot i and its desired po-

sition,

• Robot i does not detect its neighbor necessary to

determine its preferred position.

If this situation occurs, the robot receives the order to

follow the edge of the obstacle, keeping the obstacle

on its right if i ∈ S

, or its left if i ∈ S

. This be-

havior is called wall-following. The robot continues

to wall-follow around the obstacle until none of the

above conditions is satisﬁed. After that, it assumes its

desired position again. If all robots have past the ob-

stacle, each robot is again able to reach its desired po-

sition in the preferred formation. In particular, robots

N/2 and N/2+ 1 will meet again in their desired rel-

ative position. When this happens a signal is sent to

all robots with the message that the group has past the

obstacle.

A simulation of the above described algorithm is

presented in Figure 4 with N = 10 and m = 6.

Remark. It may occur that a robot cannot reach its

desired position because it is located too far away

from its present position. Then the robot simply rides

towards the desired position at the maximum allowed

velocity, trying to catch up.

Remark. If the number of robots N

∗

in the

(sub)group is not even, then the indices of the robots

where the robot group splits are ⌊N

∗

/2⌋ and ⌈N

∗

/2⌉,

where ⌊.⌋ is the function giving the largest integer less

than or equal to its argument, and similarly, ⌈ .⌉ gives

the smallest integer greater than or equal to its argu-

ment.

2.3 Multiple Obstacles

Suppose the robot group is already split into two sub-

groups and a robot in one of the subgroups encounters

a second obstacle. The above obstacle avoidance al-

gorithm can be made modular in order to solve this

problem. A group can only split if both robots at the

extremities of the group are leader robots, similar to

the initial conﬁguration. Assume group S

encoun-

ters a second obstacle. Robot N/2 is then turned into

a leader robot. Instead of following a strip boundary it

is ordered to follow the edge of the ﬁrst obstacle, un-

til it meets its neighbor N/2+ 1 or until group S

has

past the second obstacle. In the latter case, robot N/2

takes on its role as a follower of robot N/2−1 again,

in the former case it turns into a follower of N/2+ 1.

The group S

is split into the middle and the algo-

rithm described in the previous section is performed

with leader robots 1 and N/2. In order for each robot

to know which role to assume, it keeps track of how

many times its subgroup is split.

Clearly, the number of times this splitting can be

repeated is limited. We require a subgroup to consist

of at least 3 robots: two leader robots on each side

of the group, plus at least one robot in the middle at-

tempting to follow both leaders while maintaining the

formation structure. The middle robot ensures that the

A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE ROBOTS

discs of sensed area of the separate robots overlap for

all time instants.

2.4 Adaptation of the Basic Algorithm

Consider a worst case scenario as sketched in Fig-

ure 5. The robot formation splits into two subgroups,

and the group on the left hand side moves through

the gap between the obstacle and the left boundary of

the scanning strip. Once past the gap the robots in

this subgroup have to spread out, since the distance

between the obstacle and the left boundary increases

and we want to sense all of free space between the

boundary and the obstacle. The obstacle has such a

shape that the robots have to spread out across almost

the entire width of the scanning strip before meet-

ing a robot member of the right subgroup. The basic

algorithm is modiﬁed as follows. When robot N/2

(resp. N/2+ 1) encounters the obstacle, it is now pro-

grammed to follow the obstacle’s edge until it meets

its neighbor N/2+ 1 (resp. N/2). Additionally, it en-

sures that its neighbor N/2− 1 (resp. N/2+ 1) stays

in its detection range by sending a signal to the other

robots of its subgroup to increase the angle π/4 of (3).

This changes the desired position of each robot in the

subgroup resulting in a stretching out of the group,

as far as necessary. The above modiﬁed algorithm

Figure 5: A depiction of the worst case scenario in the al-

gorithm.

justiﬁes our choice of initial formation and width of

the scanning strip. If we had naively chosen a value

(N − 1)d as the width of a scanning strip, the initial

preferred robot formation would be able to span this

entire distance, namely by forming a line with the an-

gles deﬁned in Section 2.1 equal to α

= −β

= π/2.

However, one subgroup, consisting of only half of the

number of robots, would not be able to span this dis-

tance, resulting in either an error message from the al-

gorithm or in unscanned areas, if a situation described

in Figure 5 was encountered.

Closely related to this observation is the choice to

split the robot group precisely in the middle. Since the

sensor range of each robot is limited and the robots

operate in an unknown environment, the shape of

each obstacle is unknown. To guarantee that the area

around the obstacle is fully covered by the sensors, we

have to supply a sufﬁcient number of robots to both

sides of the obstacle. For instance, when the shape

of the obstacle in Figure 5 is known a priori, one can

decide to send more than half of the robots to the left

of the obstacle. Consider the case where the obstacle

is reﬂected with respect to the vertical axis. In this

case sending less than half of the robots to the right

would lead to uncovered areas or an error message in

the algorithm. With limited sensor information it is

not possible to discriminate between the situation of

Figure 5 and its reﬂected version. This leads us to

always split the group into two equal parts.

An alternative solution for this problem could be

a more intelligent algorithm where individual robots

transmit more sensor data to the others in order to ﬁnd

possible bounds on the size of the encountered obsta-

cle. If the obstacle is small, a better way to split is

right at the place where the obstacle is encountered.

The robots do not have to deviate much from the pre-

ferred formation, which decreases the probability on

error messages from deforming the robot conﬁgura-

tion. This idea may be incorporated in future work.

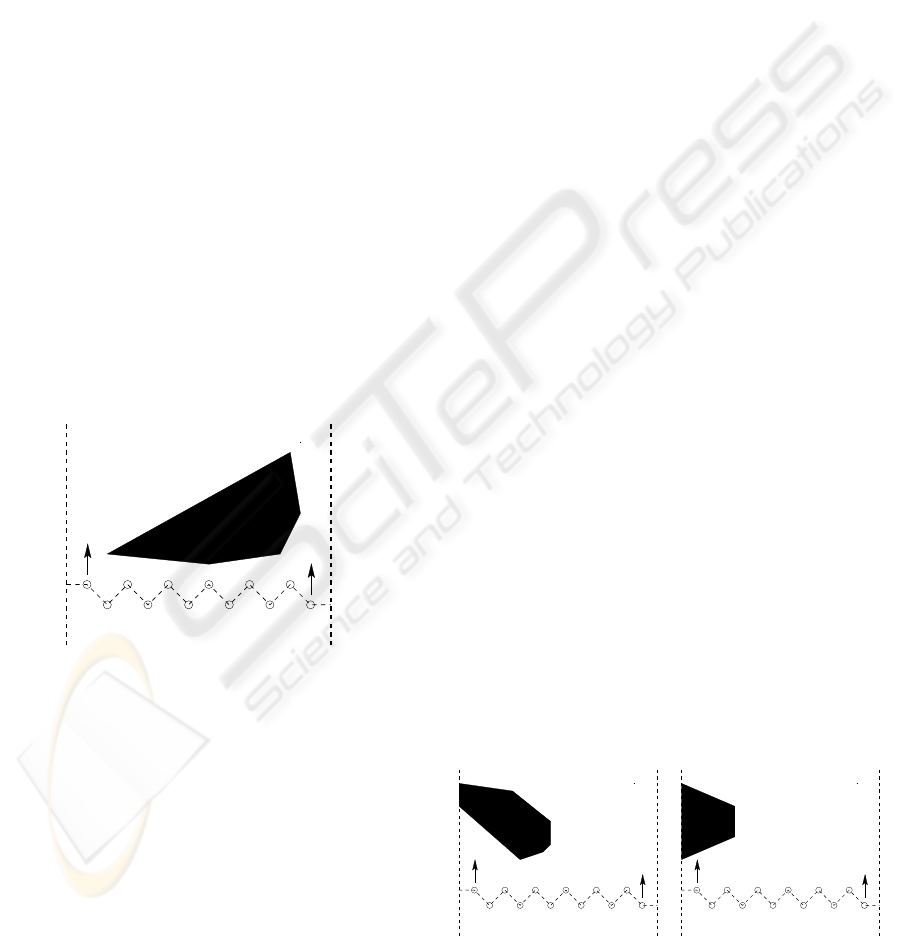
2.5 Obstacles Located on the Boundary

between Two Strips

Throughout the paper the obstacles are assumed to

have a convex shape, in order to avoid robot groups

getting stuck in a dead end. However, there is one

case of dead ends we cannot avoid by the above as-

sumption. A dead end can occur when an obstacle is

located on the boundary between two strips, as pre-

sented on the left hand side of Figure 6. Since the

robots have limited sensor information, they cannot

conclude a priori whether an encountered obstacle

stretches out into a neighboring strip or not. We are

forced to let the algorithm run until a dead end is ob-

served.

Figure 6: Two situations where an obstacle is located on

the boundary between strips. On the left hand side a dead

end situation arises; on the right hand side one of the leader

robots guides the group around the obstacle.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Before tackling the dead end problem, let us treat

the case presented on the right hand side of Figure 6,

which does not lead to a dead end situation. Con-

sider an (x,y)-frame with the y-axis parallel to the

strip boundary, and directed into the driving direction

of the leader robots. When the leader robot encoun-

ters the obstacle, the algorithm assigns to this leader

a wall-following procedure around the obstacle. The

leader keeps the obstacle either on its right or left (de-

pending on its position in the robot formation) while

moving into the interior of the strip away from the

strip boundary. As can be concluded from the picture,

the y-coordinate of the leader increases while mov-

ing around the obstacle. We wish to keep the veloc-

ity component of the leader robot parallel to the strip

boundary equal to v. Since the robot deviates from

its straight path parallel to the strip boundary, this im-

plies it has to speed up. When the leader reaches the

strip boundary again, it switches back to the original

task of moving parallel to the boundary.

Now consider the left hand side of Figure 6. A

dead end is detected by the algorithm when two con-

ditions are satisﬁed:

• one of the leader robots cannot move into the de-

sired direction parallel to the strip boundary, be-

cause an obstacle is blocking the way.

• when the leader robot starts wall-following the

obstacle as described above, the value of its y-

coordinate decreases.

As soon as a dead end is observed by the leader robot,

it changes its behavior and stops its wall following al-

gorithm. Instead, it projects its corresponding strip

boundary (N/2− 1)d/8 units outwards and resumes

the original scanning algorithm with respect to the

new boundary. If the extra width turns out to be insuf-

ﬁcient to guide the robot subgroup around the obsta-

cle outside of the original scanning strip, the bound-

ary is projected a second (third,...) time. This way the

subgroup which was stuck in the dead end is guided

around the obstacle. When both subgroups reestab-

lish contact, the leader robot returns to the original

strip boundary. This behavior is faster and easier to

implement than a turning-back scenario, where the

subgroup of robots which meets a dead end retraces

it steps to go around the obstacle inside the original

scanning strip.

Remark. The above situation with a solid wall as

strip boundary, forcing a turning-back maneuver, is

precluded.

2.6 The Transition from One Strip to

the Next

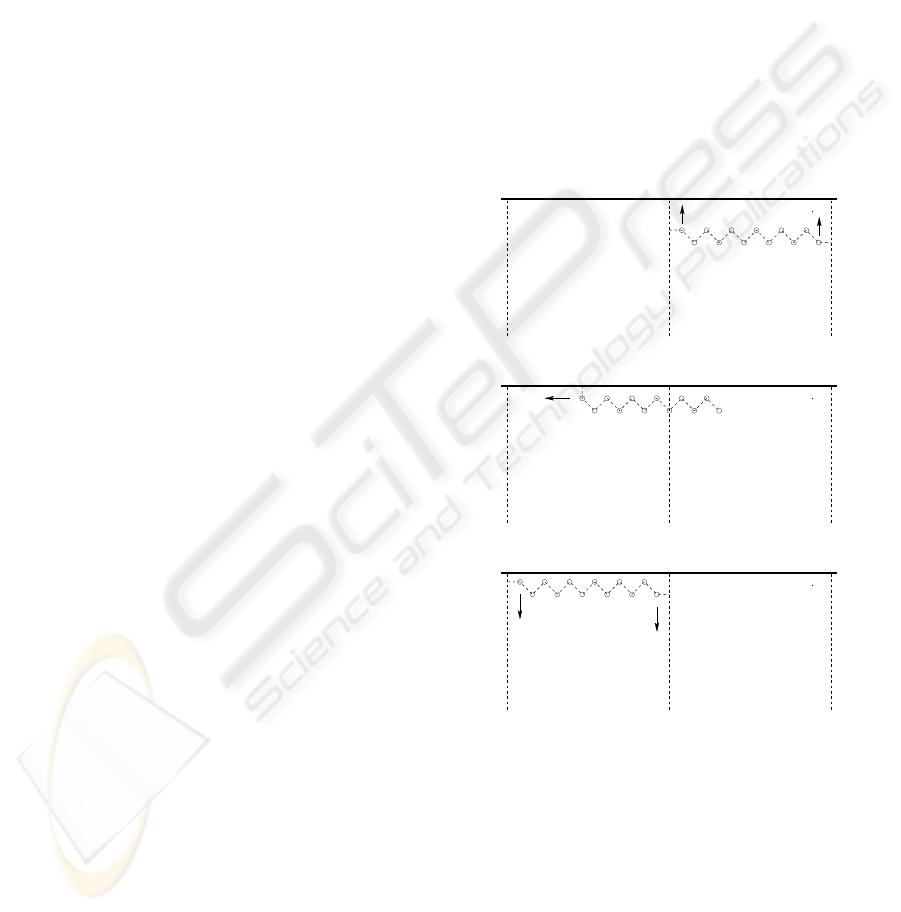
When the robot group reaches the end of a scanning

strip, it needs to be transported to the next strip. This

is done in a few easy steps. Consider the situation of

Figure 7. First the right leader changes its behavior

into that of a robot in the interior of the formation, i.e.

it tries to attain the desired formation. The left leader

moves (N/2 − 1)d units to the left perpendicular to

the strip boundary. The rightmost robot resumes its

leader role and all robots reverse their forward direc-

tion with respect to the desired direction in the previ-

ous strip. Naturally, every time the end of a strip is

reached, the roles of left and right leader alternate, so

that the robot group does not get trapped into a loop

consisting of two strips.

Figure 7: The robot group moves from the end of a scanning

strip to the start of the next strip.

3 COMPARISON WITH

COMPLETE COVERAGE

ALGORITHMS

The algorithm presented in this paper is inspired by

the complete coverage algorithm presented in (Rek-

leitis et al., 2004), which is depicted in Figure 8. The

authors of (Rekleitis et al., 2004) propose the follow-

A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE ROBOTS

ing robot conﬁguration: 2 leader robots, following

the strip boundaries, and a number of interior robots,

traveling back and forth between the strip boundaries

physically covering all the free space. Contrary to the

algorithm proposed in the present paper, the leader

robots maintain line-of-sight contact between each

other. When an obstacle appears between the two

leaders the line-of-sight contact is lost and the obsta-

cle is detected. An appropriate control action is then

taken by splitting the platoon and the algorithm is re-

peated on both sides of the obstacle. The splitting

procedure includes the creation of two extra leader

robots, as shown in Figure 8. Remark that the lead-

ers are allowed to move ahead of the rest of the robot

group and hence group coherence is not maintained

or desired, contrary to our approach.

Figure 8: A depiction of the complete coverage algorithm

by Rekleitis et al.

In the remainder of this section we will compare

speed of performance of the present algorithm with

the algorithm of (Rekleitis et al., 2004). In order to

do so, realistic distance values are considered. Chem-

ical vapor sensors detecting mines have a range s

1.70 m. Obstacles and other robots can be detected by

laser based sensors with a range of s

= 3.3 m such

that (1) is satisﬁed. Assume the robots themselves

possess a diameter of 0.3 m and set the ﬁxed interdis-

tance d between neighboring robots in the preferred

formation equal to s

. With N the number of robots in

the group, this yields a strip width of 1.65(N − 2) m.

When no obstacles are encountered, the robots are

allowed to move at a preset maximum velocity v

max

In the algorithm of the present paper v

max

is directed

parallel to the strip boundary, whereas the interior

robots in (Rekleitis et al., 2004) travel back and forth

inside the strip at v

max

. It can be proven that for the

latter case with the values given above the speed of

progress parallel to the strip boundary is v

max

/6.

In the presence of obstacles a comparison is more

difﬁcult. First consider the complete coverage algo-

rithm (Rekleitis et al., 2004). As can be concluded

from Figure 8, in the presence of an obstacle the

robots will advance faster parallel to the strip bound-

ary, since the space occupied by the obstacle does not

have to be covered. The robot group will proceed

fastest when the shape of the obstacle is such that

there is no space left for the robots to travel back and

forth between obstacle and strip boundary. Hence, de-

pending on size and shape of the obstacle the robots

advance with a speed between v

max

/6 and v

max

. Now,

consider the algorithm of the present paper. Some in-

terior robots perform wall-following around the ob-

stacles. This implies their path is longer than the path

of the leader robots. If the leader robots keep mov-

ing at the maximum allowed velocity, those interior

robots will never again be able to reach their desired

position inside the formation after the obstacle is past.

Hence, when an obstacle is encountered the leaders

have to take on a velocity v

which is smaller than

max

. This velocity v

is determined as follows. The

middle robots N/2 and N/2 + 1 transmit their posi-

tions via the other robots to their respective leader

robots. The leaders adjust their velocity v

such that

the difference between their y-coordinate and the y-

coordinate of the corresponding robot N/2 or N/2+1

stays at all time within a prespeciﬁed bound. The

middle robots only slow down the group signiﬁcantly

during the ﬁrst and last stage of their obstacle follow-

ing, i.e. when moving away from or towards the strip

boundary without signiﬁcantly advancing parallel to

it. As soon as there is enough free space ahead of the

middle robots, the subgroup is again allowed to move

parallel to the strip boundary with a speed close to

max

From the above observations the following is con-

cluded. The robot group in the present algorithm

slows down to pass an obstacle, but for most of the

time the speed will be close to v

max

. The robot group

of the complete coverage algorithm speeds up when

passing an obstacle, but for most obstacles the algo-

rithm still requires a robot group moving back and

forth between the obstacle and the strip boundary.

This implies that the increased speed will on average

be closer to v

max

/6 than to v

max

. Hence, in generic

cases, the present algorithm performs faster than the

complete coverage strategy even in the presence of

obstacles.

4 CONCLUSIONS

The present paper described a novel strategy for

multi-robot exploration of an unknown environment

with guarantee of total sensor coverage. The algo-

rithm we proposed is inspired by methods used for

complete coverage as described in (Rekleitis et al.,

2004). We took advantage of the fact that only com-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

plete sensor coverage is required. We let the robots

form a spring-like formation which scans the area in

strips. In the presence of obstacles the formation is

deformed and split in two in order to circumvent the

obstacles and to adapt to the varying width of the free

space.

ACKNOWLEDGEMENTS

This paper presents research results of the Belgian

Programme on Interuniversity Attraction Poles, ini-

tiated by the Belgian Federal Science Policy Ofﬁce.

The scientiﬁc responsibility rests with its authors.

REFERENCES

Burgard, W., Moors, M., Stachniss, C., and Schneider, F.

(2005). Coordinated multi-robot exploration. IEEE

Transactions on Robotics, 21(3):376–386.

Choset, H. (2001). Coverage for robotics – a survey of re-

cent results. Annals of Mathematics and Artiﬁcial In-

telligence, 31:113–126.

Cort

es, J., Mart

ınez, S., Karatas, T., and Bullo, F. (2004).

Coverage control for mobile sensing networks. IEEE

Transactions on Robotics and Automation, 20(2):243–

255.

Gage, D. (1995). Many-robots mcm search systems. In

Proceedings of Autonomous Vehicles in Mine Coun-

termeasures Symposium.

Kerr, W., Spears, D., Spears, W., and Thayer, D. (2004).

Two formal gas models for multi-agent sweeping and

obstacle avoidance. In Formal Approaches to Agent-

Based Systems, Third International Workshop, pages

111–130.

Keymeulen, D. and Decuyper, J. (1994). The ﬂuid dynam-

ics applied to mobile robot motion: the stream ﬁeld

method. In Proceedings of 1994 IEEE International

Conference on Robotics and Automation, pages 378–

385, Piscataway, NJ, USA.

Kong, C. S., Peng, N. A., and Rekleitis, I. (2006). Dis-

tributed coverage with multi-robot system. In Pro-

ceedings of 2006 IEEE International Conference on

Robotics and Automation, pages 2423–2429, Orlando,

Florida, USA.

Kurabayashi, D., Ota, J., Arai, T., and Yosada, E. (1996).

Cooperative sweeping by multiple robots. In Proc.

1996 IEEE International Conference on Robotics and

Automation.

Ota, J. (2006). Multi-agent robot systems as distributed au-

tonomous systems. Advanced engineering informat-

ics, 20:59 – 70.

Rekleitis, I., Lee-Shue, V., New, A. P., and Choset, H.

(2004). Limited communication, multi-robot team

based coverage. In Proc. 2004 IEEE International

Conference on Robotics and Automation.

Wong, S. and MacDonald, B. (2004). Complete coverage

by mobile robots using slice decomposition based on

natural landmarks. In Proc. Eighth Paciﬁc Rim Inter-

national conference on Artiﬁcial Intelligence. Lecture

Notes in Artiﬁcial Intelligence., volume 3157, pages

683–692.

Zheng, X., Jain, S., Koenig, S., and Kempe, D. (2005).

Multi-robot forest coverage. In Proceedings of the

IEEE International Conference on Intelligent Robots

and Systems.

A NOVEL STRATEGY FOR EXPLORATION WITH MULTIPLE ROBOTS