COMPARISON OF FINE NEEDLE BIOPSY CYTOLOGICAL IMAGE

SEGMENTATION METHODS

Maciej Hrebie

n, Piotr Ste

c and Józef Korbicz

Institute of Control and Computation Engineering, University of Zielona Góra

ul. Podgórna 50, 65-246 Zielona Góra, Poland

Keywords:

Cytology, image processing, segmentation.

Abstract:

This paper describes an early stage of cytological image recognition and presents a comparision of two hybrid

segmentation methods. The analysis includes the Hough transform with conjunction to the watershed algo-

rithm and with conjunction to the active contours techniques. One can also ﬁnd here a short description of

image pre-processing and an automatic nucleuses localization mechanisms used in our approach. Preliminary

experimental results collected on a hand-prepared benchmark database are also presented with short discussion

of common errors and possible future problems.

1 INTRODUCTION

Construction of a fully automatic cancer diagnosis

system is a challenging task. In last decade we can ob-

serve a very dynamic growth in number of researches

conducted in this area not only by university centers

but also by commercial institutions (Kimmel et al.,

2003). Because the breast cancer is becoming most

common disease of the present female population,

much attention of the present-day researchers is di-

rected to this issue. The attention covers not only cur-

ing the external effects of the disease but also its fast

detection in its early stadium.

The nucleus of the cell is the place where breast

cancer malignancy can be observed. Therefore, it is

crucial for any camera based automatic diagnosis sys-

tem to separate the cells and their nuclei from the

rest of the image content. Until now many segmen-

tation methods were proposed (Gonzalez and Woods,

2002; Pratt, 2001; Russ, 1999) but unfortunately

each of them introduces different kinds of additional

problems and usually works in practice under given

assumptions and/or needs end-user’s interaction/co-

operation. Since many cytological projects assume

rather full automation and real-time operation with

high degree of efﬁcacy, a method free of drawbacks

of already known approaches has to be constructed.

In this paper two hybrid methods of cytological

image segmentation are presented, that is the Hough

transform with conjunction to the watershed algo-

rithm and with conjunction to the active contours

techniques. One can also ﬁnd here a short descrip-

tion of image pre-processing and fully automatic nu-

clei localization mechanisms used in our approach.

2 PROBLEM FORMULATION

Mathematical formulation of the segmentation pro-

cess is very difﬁcult because it is a poorly conditioned

problem. Thus we give here only some informal deﬁ-

nition of the problem we have to face.

What we have on input is a cytological material

obtained using the Fine Needle Biopsy technique and

imagined with a Sony CCD Iris camera mounted atop

of an Axiophot microscope. The material comes from

female patients of Zielona Góra’s Onkomed medical

center (Marciniak et al., 2005). The 704 × 576 pixel

image itself is coded using the RGB colourspace and

is not subject of any kind of lossy compression.

What we expect on output is a binary segmenta-

tion mask with one pixel separation rule which will

allow us to more robust morphometric parameters es-

timation in our future work. Additionally, the algo-

rithm should be insensitive to colours of contrasting

305

Hrebie

n M., Ste

c P. and Korbicz J. (2007).

COMPARISON OF FINE NEEDLE BIOPSY CYTOLOGICAL IMAGE SEGMENTATION METHODS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 305-310

DOI: 10.5220/0001645603050310

 SciTePress

(a) (b)

Figure 1: Exemplary fragment of: (a) cytological image,

(b) appropriate segmentation mask.

pigments used for preparation of the cytological ma-

terial (see an example in Fig. 1).

3 IMAGE PRE-SEGMENTATION

3.1 Pre-processing

The colour components of an image do not carry as

important information as the luminosity does, so they

can be removed to reduce processing complexity in

stages that require only e.g. gradient estimations.

An RGB colour image can be converted to greyscale

by removing blue and red chrominance components

from the image deﬁned in YCbCr colour space (Pratt,

2001).

Since the majority of images we deal with have

low contrast, an enhancement technique is needed to

improve their quality. In our approach we use sim-

ple histogram processing with linear transform of im-

age levels of intensities, that is the cumulated sum ap-

proach (Russ, 1999). The contrast correction opera-

tion is conducted for each colour channel separately

resulting in an image being better-deﬁned for later

stages of the presented hybrid segmentation methods

(see Fig. 2).

3.2 The Background of the Algorithm

If we look closely at the nuclei we have to segment,

they all have elliptical shape. Most of them remind

ellipse but unfortunately detection of ellipse which

is described by two parameters a and b (x = acosα,

y = bsinα) and which can be additionally rotated is

computationally expensive. The shape of ellipse can

be approximated by a given number of circles. De-

tection of circles is much more simpler in the sense

of required computations because we have only one

parameter, that is the radius R. This observations and

simpliﬁcations constitute grounding for fast nucleus

pre-segmentation algorithm – in our approach we try

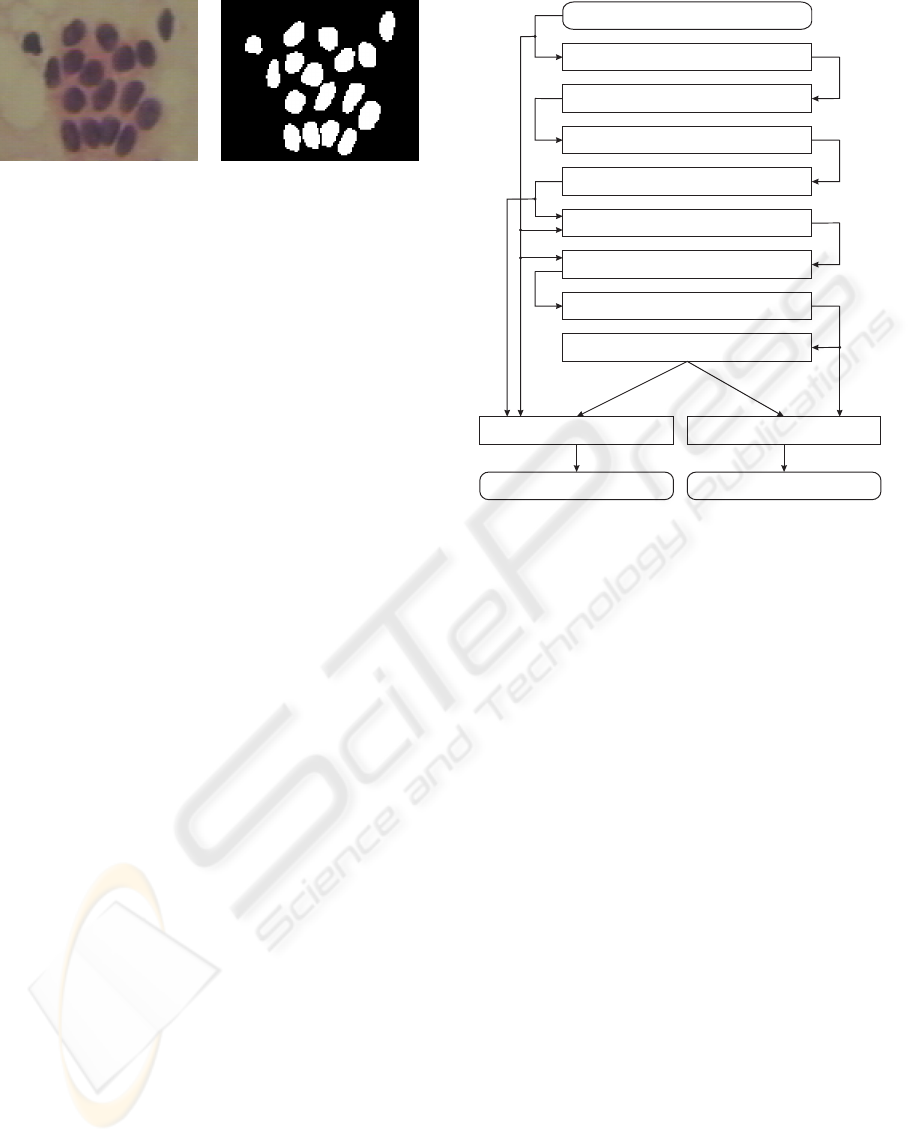
Inputimage

Contrastenhancement

RGBtogreyscaleconversion

Gradientestimation

Pre-segmentation(circlesdetection)

Avgbackgroundcolourestimation.

Terrain modeling

Smoothing(noisereduction)

Nucleilocalization

Activecontouringsegmentation

Segmentationmask

Watershedsegmentation

Segmentationmask

Figure 2: Flow graph of the presented solutions.

to ﬁnd such circles with different radii in a given fea-

ture space.

3.3 Circles Detection

The Hough transform (Toft, 1996;

Zorski, 2000) can

be easily adopted for the purpose of circle detection.

The transform in the discrete space can be deﬁned as:

discr

(R,

j) =

i+R

∑

i−R

j+R

∑

j−R

g(i, j)δ



(i−

+ ( j−

− R



, (1)

where g is a two dimensional feature image and δ is

the Kronecker’s delta (equal to unity at zero) which

deﬁnes sum only over the circle. The HT

discr

plays

the role of accumulator which accumulates levels of

feature image g similarity to circle placed at the (

position and deﬁned by the radius R.

The feature space g can be created by many differ-

ent ways. In our approach we use gradient image as

the feature indicating nucleus’ occurrence or absence

in a given fragment of cytological image. The gra-

dient image is a saturated sum of gradients estimated

in eight directions on greyscale image prepared in the

pre-processing stage. The base gradients can be cal-

culated using e.g. Prewitt’s, Sobel’s mask methods or

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

306

Figure 3: Inﬂuence of θ threshold value on objects’s cover

and lack of differences (left) and overcovering (right) for

Prewitt (×), Sobel (∗), heavy (•) and light (+) base gradient

masks (experiments performed on a randomly selected 346

element Zielona Góra’s Onkomed (Marciniak et al., 2005)

cytological benchmark database for radii in the 4-21 pixel

range).

(a) (b)

Figure 4: Exemplary results of the pre-segmentation stage

for two different θ threshold strategies: (a) high and (b) low.

their heavy or light versions (Gonzalez and Woods,

2002; Tadeusiewicz, 1992).

3.4 Final Actions

Thresholding the values in the accumulator by a given

θ value can lead us to a very good pre-segmentation

mechanism with the lower threshold strategy (see for

instance Fig. 4). Since the threshold value strongly

depends on the database and used feature image g

(Fig. 3), the method can only be used as a pre-

segmentation stage. Smaller value of the thresh-

old causes fast removal of non-important information

from the background what can constitute a base for

more sophisticated and going into details algorithms.

4 IMAGE SEGMENTATION

4.1 Terrain Modeling

The results obtained from the pre-segmentation stage

can lead us to the estimation of average background

colour. This information can be used to model the nu-

clei as a colour distance between background and ob-

jects what fulﬁls requirements of lack of any colour

(a) (b) (c)

Figure 5: Exemplary fragment of: (a) cytological im-

age, (b) Euclidian distance to the mean background colour,

dependency in imaged material (the colour of con-

trasting pigments may change in the future). In

our research we tried few distance metrics: Manhat-

tan’s, Chebyshev’s, absolute Hue value from HSV

colourspace but Euclidian one gives the best visual

results (Fig. 5ab).

Since the modeling distance can vary in local

neighborhood (see Fig. 5b) mostly because of cam-

era sensor simpliﬁcations, a smoothing technique is

needed to reconstruct the nuclei shape. The smooth-

ing operation in our approach relies on the fact that

this sort of 2D signal can be modeled as a sum of si-

nusoids (Madisetti and Williams, 1997) with deﬁned

amplitudes, phase shifts and frequencies. Cutting all

low amplitude frequencies off (leaving only a few sig-

niﬁcant ones with the highest amplitude) will result

in a signal deprived our problematic local noise effect

(Fig. 5c).

4.2 Nuclei Localization

Localization of objects on a modeled map of nu-

clei can be performed locally using various methods.

In our approach we have chosen evolutionary (1+1)

search strategy (Arabas, 2004) mostly because it is

simple, quite fast despite appearances, can be easily

parallelized due to its nature and it settles very good

in local extrema what is very important in our case.

The used watershed segmentation algorithm

forced us to create two population of individuals. The

ﬁrst population is localizing the background. Speci-

mens are moved with a constant movement step equal

to unity and the movement is preferred to the places

with a smaller density of population to maximize

background coverage. The second population is lo-

calizing the nuclei. Specimens are moved with a ex-

ponentially decreasing movement step to very fast

group the population near local extrema in ﬁrst few

epochs and to ﬁnally work on details in the ending

ones. The movement of individuals is preferred to the

places with a higher population density to create the

effect of nuclei localization.

The change for the better position of an individ-

COMPARISON OF FINE NEEDLE BIOPSY CYTOLOGICAL IMAGE SEGMENTATION METHODS

307

(a) (b)

Figure 6: Exemplary localization: (a) screenshot after

8 epochs, (b) ﬁnal result (localization points are marked

with red asterisks).

ual searching for nuclei is calculated as a product

of randomly generated distance with normal distri-

bution N(0, 1) and an decreasing in time radius r

max



max



max

, where R

max

is the maximal radius

detected by the Hough transform. Specimens cover-

ing background are generated in a similar way except

R = 1 during mutation.

The ﬁtness function calculates the average height

of the terrain in a given position including nearest

neighborhood deﬁned by the smallest radius detected

by the Hough transform in the pre-segmentation

stage. Such deﬁnition of the ﬁtness function avoids a

possible split of population, localized near a nucleus

with multimodal character of its shape, giving only

one marker for a nucleus (Fig. 6b).

Finally, the nucleus is localized in the place where

the density of the population searching for hilltops in

the modeled terrain is locally maximal.

The used active contours techniques have lower

requirements concerning nucleus localization. In this

approach it is allowed to have more than one marker

pointing the same nucleus. Thus the localization al-

gorithm in this case can be much simpliﬁed. We

need only one population, that is the one searching

for nuclei and the ﬁtness function is simply the ter-

rain height at an individuals position. Additionally, it

is allowed to have not optimal or even false localiza-

tion points what reduces number of needed iterations

of the algorithm.

4.3 Building Watersheds

The watershed segmentation algorithm is inspired by

natural observations, that is a rainy day in moun-

tains (Gonzalez and Woods, 2002; Pratt, 2001; Russ,

1999). A given image can be deﬁned as a terrain on

which nuclei correspond to valleys (upside down ter-

rain modeled in previous steps). The terrain is ﬂooded

by rainwater and arising puddles are starting to turn

into basins. When the water from one basin begins to

pour away to another, a separating watershed is cre-

ated.

The ﬂooding operation have to be stopped when

the water level reaches a given θ threshold. The

threshold should preferably be placed somewhere in

the middle between the background and a nucleus lo-

calization point. In our approach nuclei are ﬂooded

to the half of the altitude between nucleus localiza-

tion point and the average height of the background

in the local neighborhood. Since the images we have

to deal with are spot illuminated during imaging op-

eration (resulting in a modeled terrain being higher

in the center of the image and much lower in the cor-

ners) this mechanism protects the basins against being

overﬂooded and in consequence nuclei being under-

segmented. To satisfy the one pixel separation rule

the algorithm needs to have multi-label extension and

the watersheds are built only when there is a neighbor

nearby with other label.

4.4 Active Contours

An active contour segmentation is performed using

multilabel fast marching algorithm presented in (Ste

2005; Hrebie

n and Ste

c, 2006) which is extension to

the original fast marching method (FMM) developed

by Sethian (Sethian, 1998). The problem with the

original FMM is that the contour can be moved only

in one direction. This means that any error in seg-

mentation cannot be corrected and algorithm requires

additional stop condition. To deal with this problem,

multilabel extension to the classical FMM was pro-

posed.

Initialization of the multilabel fast marching is

done in similar way as it was done for the watershed

algorithm. The difference is that the watershed ini-

tialization image requires an additional processing to

leave exactly one seed per nucleus while the FMM al-

lows more seeds in one nucleus. Similar method of

initialization will allow direct comparison of the seg-

mentation results.

Initial contour propagation is similar to original

FMM method. Expansion of the contour is governed

by a propagation speed deﬁned globally for all the

contours. Speed is based on the difference between

mean colour in the initialization area and colour of

the pixel under the contour:

F =

|g(x, y) − ¯g(i)|

+ 1

, (2)

where g(x, y) is the colour under the contour and ¯g(i)

is the mean colour under the i-th segment. Such a

speed deﬁnition slows down the contour near the de-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

308

tected object boundary what increases probability of

contours meeting near nucleus boundary.

When two segments meet, mean colour of the seg-

ments is compared. Comparison is taken at the point

where contours start to overlap. When difference be-

tween mean colours from these two segments is below

certain threshold segments are merged into one. To

ensure maximum efﬁciency, labels from the smaller

segment are changed to the value of those from the

larger segment. Additionally, new mean colour for

the segment is calculated from mean colours of con-

nected segments.

If two segments that meet are not classiﬁed to

be merged, the propagating segment can push back

another segment under certain circumstances. At

the meeting point differences between current pixel

colour and mean colour of each segment is compared.

Segment with lower difference value wins and re-

places current label with its own. Replacement is per-

formed as long as condition is meet. Contour that was

pushed back cannot be propagated farther at places

where its labels was replaced by another contour.

Contour points that cannot be moved are no longer

considered during calculations. Since contour can be

pushed back only once, there is no oscillation at the

object boundary known from the classical active con-

tour methods. Additionally reduction of the contour

length increases performance of the algorithm.

The presented algorithm stops propagation when

all image points are assigned to segments and there

is no segment that could push back another segment.

The algorithm cannot run inﬁnitely because oscilla-

tions between segments are impossible. No segment

can visit twice the same area. Namely, when a seg-

ment was pushed back by another segment, it cannot

get the lost pixels back.

4.5 Exemplary Results

Exemplary results of the presented watershed seg-

mentation method and common errors observed on

our hand-prepared benchmark database can be di-

vided into four classes:

• class 1: good quality images with only small ir-

regularities and rarely generated subbasins (basin

in another basin) (Fig. 7ab),

• class 2: errors caused by fake circles created by

spots of fat (Fig. 7cd),

• class 3: mixed nucleus types: red and purple

in this case and those reds which are more pur-

ple than yellow (background) are also segmented

what is erroneous (Fig. 7ef),

(a) (b)

(e) (f)

(g) (h)

Figure 7: Exemplary results of the watershed segmentation.

• class 4: poor quality image with a bunch of

nuclei glued together what causes basin’s over-

ﬂooding and in consequence undersegmentation

(Fig. 7gh).

Conducted experiments show that the watershed

algorithm gives 68.74% on the average agreement

with the hand-prepared templates using simple XOR

metric. As one can easily notice most errors are lo-

cated at boundaries of nuclei (see for instance Fig. 8)

where the average distance between edges of seg-

mented and reference objects is about 3.28 pixles on

the average. This causes the XOR metric to be un-

derestimated as a consequence of not very heigh level

of water ﬂooding the modeled terrains. For the active

contours algorithm the situation is very similar, that

is the XOR metric gives 22.32% score and the aver-

age distance is equal to 4.1 pixels. Despite the under-

estimation fact the shape of nuclei seems to be pre-

served what is important for our future work, that is

estimation of morphometric parameters of segmented

nuclei.

COMPARISON OF FINE NEEDLE BIOPSY CYTOLOGICAL IMAGE SEGMENTATION METHODS

309

(a) (b)

Figure 8: Common XOR metric errors for: (a) the water-

shed and (b) the active contours method.

5 CONCLUSIONS

Conducted preliminary experiments show that the

Hough transform adopted for circle detection in the

pre-segmentation stage, the (1+1) search strategy

used for automatic nuclei localization, the watershed

algorithm and the active contours techniques used for

the ﬁnal segmentation stage can be effectively used

for the segmentation of cytological images.

The problem regarding fake circles created by

spots of fat and unwanted effects it gives in the ﬁ-

nal output should also be considered and eliminated

in future work. Images with mixed nucleus type still

constitute a challenge because it seems to be impos-

sible to detect only one type without end-user’s in-

teraction and when there should not be any depen-

dencies and assumptions concerning colour of con-

trasting pigments used to prepare cytological mate-

rial. The proposal hybrid methods should also be ex-

tended to perform better on poor quality images or a

fast classiﬁer should be constructed to reject too poor

(or even fake) inputs.

Summarizing, the presented solutions are promis-

ing and give a good base for our further research in the

area of cytological image segmentation. Additionally,

all preparation steps including pre-segmentation and

the automatic nucleus localization stage can be reused

with other segmentation algorithms which need such

a information.

Performance of both algorithms is comparable.

There was no result that clearly shows superiority of

one algorithm above the other. The outcome was de-

pendent on the used metric. Visually, segmentation

results from both algorithms look very similar (see

Fig. 8). Both algorithms have problems with the tight

clusters of nuclei. They are usually detected as a sin-

gle object.

Time reaction of both algorithms is similar too

and it takes several seconds on today’s PCs per im-

age to give the ﬁnal segmentation mask. All prepara-

tion steps are much more time consuming (2-3 min-

utes) but authors believe that it can be signiﬁcantly

reduced mostly because of the fact that this steps

were simulated in MATLAB environment. Taking

the advantage of today’s multi-core machines, thread-

oriented operating systems, the nature of used algo-

rithms which are easy to parallelize and rewriting

them using native code generating programming lan-

guage can speed up the whole process signiﬁcantly. A

dedicated hardware could also be considered.

REFERENCES

Arabas, J. (2004). Lectures on Evolutionary Algorithms.

WNT. (in Polish).

Gonzalez, R. and Woods, R. (2002). Digital Image Process-

ing. Prentice Hall.

Hrebie

n, M. and Ste

c, P. (2006). The Hough transform and

active contours in segmentation of cytological images.

In Proc. of the 9th Int. Conf. on Medical Informat-

ics and Technology – MIT 2006, pages 62–68, Wisła-

Malinka, Poland.

Kimmel, M., Lachowicz, M., and

Swierniak, A. (2003).

Cancer growth and progression, mathematical prob-

lems and computer simulations. Int. Journal of Appl.

Math. and Comput. Science, Vol. 13, No. 3, Special

Issue.

Madisetti, V. and Williams, D. (1997). The Digital Signal

Processing Handbook. CRC Press.

Marciniak, A., Obuchowicz, A., Mo

nczak, R., and Kołodz-

nski, M. (2005). Cytomorphometry of ﬁne needle

biopsy material from the breast cancer. In Proc. of the

4th Int. Conf. on Comp. Recogn. Systems CORES’05,

Adv. in Soft Computing. Springer.

Pratt, W. (2001). Digital Image Processing. John Wiley &

Sons.

Russ, J. (1999). The Image Processing Handbook. CRC

Press.

Sethian, J. (1998). Fast Marching Methods and Level Set

Methods for propagating interfaces. In 29th Compu-

tational Fluid Dynamics, volume 1 of VKI Lectures

series. von Karman Institute.

Ste

c, P. (2005). Segmentation of Colour Video Sequences

Using Fast Marching Method, volume 6 of Lecture

Notes in Control and Computer Science. University

of Zielona Góra Press, Zielona Góra, Poland.

Tadeusiewicz, R. (1992). Vision Systems of Industrial

Robots. WNT. (in Polish).

Toft, P. (1996). The Radon Transform. Technical University

of Denmark. Ph.D. Thesis.

Zorski, W. (2000). Image Segmentation Methods Based on

the Hough Transform. Studio GiZ Warszawa. (in Pol-

ish).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

310