
NONLINEAR PROGRAMMING IN APPROXIMATE DYNAMIC
PROGRAMMING
Bang-bang Solutions, Stock-management and Unsmooth Penalties
Olivier Teytaud and Sylvain Gelly
TAO (Inria, Univ. Paris-Sud, UMR CNRS-8623)
Keywords:
Evolutionary computation and control, Optimization algorithms.
Abstract:
Many stochastic dynamic programming tasks in continuous action-spaces are tackled through discretization.
We here avoid discretization; then, approximate dynamic programming (ADP) involves (i) many learning
tasks, performed here by Support Vector Machines, for Bellman-function-regression (ii) many non-linear-
optimization tasks for action-selection, for which we compare many algorithms. We include discretizations
of the domain as particular non-linear-programming-tools in our experiments, so that by the way we compare
optimization approaches and discretization methods. We conclude that robustness is strongly required in the
non-linear-optimizations in ADP, and experimental results show that (i) discretization is sometimes inefficient,
but some specific discretization is very efficient for ”bang-bang” problems (ii) simple evolutionary tools out-
perform quasi-random in a stable manner (iii) gradient-based techniques are much less stable (iv) for most
high-dimensional ”less unsmooth” problems Covariance-Matrix-Adaptation is first ranked.
1 NON-LINEAR OPTIMIZATION
IN STOCHASTIC DYNAMIC
PROGRAMMING (SDP)
Some of the most traditional fields of stochastic dy-
namic programming, e.g. energy stock-management,
which have a strong economic impact, have not been
studied thoroughly in the reinforcement learning or
approximate-dynamic-programming (ADP) commu-
nity. This is damageable to reinforcement learn-
ing as it has been pointed out that there are not yet
many industrial realizations of reinforcement learn-
ing. Energy stock-management leads to continuous
problems that are usually handled by traditional lin-
ear approaches in which (i) convex value-functions
are approximated by linear cuts (leading to piecewise
linear approximations (PWLA)) (ii) decisions are so-
lutions of a linear-problem. However, this approach
does not work in large dimension, due to the curse of
dimensionality which strongly affects PWLA. These
problems should be handled by other learning tools.
However, in this case, the action-selection, minimiz-
ing the expected cost-to-go, can’t be anymore done
using linear-programming, as the Bellman function is
no more a convex PWLA.
The action selection is therefore a nonlinear pro-
gramming problem. There are not a lot of works deal-
ing with continuous actions, and they often do not
study the non-linear optimization step involved in ac-
tion selection. In this paper, we focus on this part: we
compare many non-linear optimization-tools, and we
also compare these tools to discretization techniques
to quantify the importance of the action-selection
step.
We here roughly introduce stochastic dynamic
programming. The interested reader is referred to
(Bertsekas and Tsitsiklis, 1996) for more details.
Consider a dynamical system that stochastically
evolves in time depending upon your decisions. As-
sume that time is discrete and has finitely many time
steps. Assume that the total cost of your decisions is
the sum of instantaneous costs. Precisely:
cost = c
1
+ c
2
+ ···+ c
T
c
i
= c(x
i
,d
i
), x
i
= f(x
i−1
,d
i−1
,ω
i
)
d
i−1
= strategy(x
i−1
,ω
i
)
where x
i
is the state at time step i, the ω
i
are a ran-
dom process, cost is to be minimized, and strategy
is the decision function that has to be optimized. We
are interested in a control problem: the element to be
optimized is a function.
Stochastic dynamic programming, a tool to solve
this control problem, is based on Bellman’s optimality
47
Teytaud O. and Gelly S. (2007).
NONLINEAR PROGRAMMING IN APPROXIMATE DYNAMIC PROGRAMMING - Bang-bang Solutions, Stock-management and Unsmooth Penalties.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 47-54
DOI: 10.5220/0001645800470054
Copyright
c
SciTePress

principle that can be informally stated as follows:
”Take the decision at time step t such that the sum
”cost at time step t due to your decision” plus ”ex-
pected cost from time step t + 1 to ∞” is minimal.”
Bellman’s optimality principle states that this
strategy is optimal. Unfortunately, it can only be ap-
plied if the expected cost from time step t + 1 to ∞
can be guessed, depending on the current state of the
system and the decision. Bellman’s optimality prin-
ciple reduces the control problem to the computation
of this function. If x
t
can be computed from x
t−1
and
d
t−1
(i.e., if f is known) then the control problem is
reduced to the computation of a function
V(t, x
t
) = E[c(x
t
,d
t
) + c(x
t+1
,d
t+1
) + ···+ c(x
T
,d
T
)]
Note that this function depends on the strategy (we
omit for short dependencies on the random process).
We consider this expectation for any optimal strategy
(even if many strategies are optimal, V is uniquely
determined as it is the same for any optimal strategy).
Stochastic dynamic programming is the computa-
tion of V backwards in time, thanks to the following
equation:
V(t,x
t
) = inf
d
t
c(x
t
,d
t
) + EV(t + 1,x
t+1
)
or equivalently
V(t,x
t
) = inf
d
t
c(x
t
,d
t
) + EV(t + 1, f (x
t
,d
t
)) (1)
For each t, V(t,x
t
) is computed for many values of x
t
,
and then a learning algorithm (here by support vec-
tor machines) is applied for building x 7→V(t,x) from
these examples. Thanks to Bellman’s optimality prin-
ciple, the computation of V is sufficient to define an
optimal strategy. This is a well known, robust so-
lution, applied in many areas including power sup-
ply management. A general introduction, including
learning, is (Bertsekas, 1995; Bertsekas and Tsitsik-
lis, 1996). Combined with learning, it can lead to pos-
itive results in spite of large dimensions. Many devel-
opments, including RTDP and the field of reinforce-
ment learning, can be found in (Sutton and Barto,
1998).
Equation 1 is used many many times during a run
of dynamic programming. For T time steps, if N
points are required for efficiently approximating each
V
t
, then there are T ×N optimizations. Furthermore,
the derivative of the function to optimize is not always
available, due to the fact that complex simulators are
sometimes involved in the transition f. Convexity
sometimes holds, but sometimes not. Binary variables
are sometimes involved, e.g. in power plants manage-
ment. This suggests that evolutionary algorithms are
a possible tool.
1.1 Robustness in Non-linear
Optimization
Robustness is one of the main issue in non-linear op-
timization and has various meanings.
1. A first meaning is the following: robust opti-
mization is the search of x such that in the neighbor-
hood of x the fitness is good, and not only at x. In par-
ticular, (DeJong, 1992) has introduced the idea that
evolutionary algorithms are not function-optimizers,
but rather tools for finding wide areas of good fitness.
2. A second meaning is that robust optimization
is the avoidance of local minima. It is known that
iterative deterministic methods are often more subject
to local minima than evolutionary methods; however,
various forms of restarts (relaunch the optimization
from a different initial point) can also be efficient for
avoiding local minima.
3. A third possible meaning is the robustness with
respect to fitness noise. Various models of noise and
conclusions can be found in (Jin and Branke, 2005;
Sendhoff et al., 2004; Tsutsui, 1999; Fitzpatrick and
Grefenstette, 1988; Beyer et al., 2004).
4. A fourth possible meaning is the robustness
with respect to unsmooth fitness functions, even in
cases in which there’s no local minima. Evolution-
ary algorithms are usually rank-based (the next iter-
ate point depends only on the fitnesses rank of previ-
ously visited points), therefore do not depend on in-
creasing transformations of the fitness-function. It is
known that they have optimality properties w.r.t this
kind of transformations (Gelly et al., 2006). For ex-
ample,
p
||x||(or someC
∞
functions close to this one)
lead to a very bad behavior of standard Newton-based
methods like BFGS (Broyden., 1970; Fletcher, 1970;
Goldfarb, 1970; Shanno, 1970) whereas a rank-based
evolutionary algorithm behaves the same for ||x||
2
and
p
||x||.
5. The fifth possible meaning is the robustness
with respect to the non-deterministic choices made by
the algorithm. Even algorithms that are considered as
deterministic often have a random part
1
: the choice of
the initial point. Population-based methods are more
robust in this sense, even if they use more random-
ness for the initial step (full random initial population
compared to only one initial point): a bad initializa-
tion which would lead to a disaster is much more un-
likely.
The first sense of robustness given above, i.e.
avoiding too narrow areas of good fitness, fully ap-
plies here. Consider for example a robot navigating
1
Or, if not random, a deterministic but arbitrary part,
such as the initial point or the initial step-size.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
48

in an environment in order to find a target. The robot
has to avoid obstacles. The strict optimization of the
cost-to-go leads to choices just tangent to obstacles.
As at each step the learning is far from perfect, then
being tangent to obstacles leads to hit the obstacles in
50 % of cases. We see that some local averaging of
the fitness is suitable.
The second sense, robustness in front of non-
convexity, of course also holds here. Convex and non-
convex problems both exist. The law of increasing
marginal costs implies the convexity of many stock
management problems, but approximations of V are
usually not convex, even if V is theoretically convex.
Almost all problems of robotics are not convex.
The third sense, fitness (or gradient) noise, also
applies. The fitness functions are based on learning
from finitely many examples. Furthermore, the gradi-
ent, when it can be computed, can be pointless even
if the learning is somewhat successfull; even if
ˆ
f ap-
proximates f in the sense that ||f −
ˆ
f||
p
is small, ∇
ˆ
f
can be very far from ∇ f.
The fourth sense is also important. Strongly dis-
continuous fitnesses can exist: obstacle avoidance is
a binary reward, as well as target reaching. Also, a
production-unit can be switched on or not, depend-
ing on the difference between demand and stock-
management, and that leads to large binary-costs.
The fifth sense is perhaps the most important.
SDP can lead to thousands of optimizations, similar to
each other. Being able of solving very precisely 95 %
of families of optimization problems is not the goal;
here it’s better to solve 95 % of any family of opti-
mization problems, possibly in a suboptimal manner.
We do think that this requirement is a main explana-
tion of results below.
Many papers have been devoted to ADP, but com-
parisons are usually far from being extensive. Many
papers present an application of one algorithm to one
problem, but do not compare two techniques. Prob-
lems are often adapted to the algorithm, and therefore
comparing results is difficult. Also, the optimization
part is often neglected; sometimes not discussed, and
sometimes simplified to a discretization.
In this paper, we compare experimentally many
non-linear optimization-tools. The list of methods
used in the comparison is given in 2. Experiments
are presented in section 3. Section 4 concludes.
2 ALGORITHMS USED IN THE
COMPARISON
We include in the comparison standard tools from
mathematical programming, but also evolutionary al-
gorithms and some discretization techniques. Evolu-
tionary algorithms can work in continuous domains
(B
¨
ack et al., 1991; B
¨
ack et al., 1993; Beyer, 2001);
moreover, they are compatible with mixed-integer
programming (e.g. (B
¨
ack and Sch
¨
utz, 1995)). How-
ever, as there are not so many algorithms that could
naturally work on mixed-integer problems and in or-
der to have a clear comparison with existing meth-
ods, we restrict our attention to the continuous frame-
work. We can then easily compare the method with
tools from derivative free optimization (Conn et al.,
1997), and limited-BFGS with finite differences (Zhu
et al., 1994; Byrd et al., 1995). We also consid-
ered some very naive algorithms that are possibly in-
teresting thanks to the particular requirement of ro-
bustness within a moderate number of iterates: ran-
dom search and some quasi-random improvements.
The discretization techniques are techniques that test
a predefined set of actions, and choose the best one.
As detailed below, we will use dispersion-based sam-
plings or discrepancy-based samplings.
We now provide details about the methods inte-
grated in the experiments. For the sake of neutrality
and objectivity, none of these source codes has been
implemented for this work: they are all existing codes
that have been integrated to our platform, except the
baseline algorithms.
• random search: randomly draw N points in the
domain of the decisions ; compute their fitness ;
consider the minimum fitness.
• quasi-random search: idem, with low discrepancy
sequences instead of random sequences (Nieder-
reiter, 1992). Low discrepancy sequences are a
wide area of research (Niederreiter, 1992; Owen,
2003), with clear improvements on Monte-Carlo
methods, in particular for integration but also
for learning (Cervellera and Muselli, 2003), opti-
mization (Niederreiter, 1992; Auger et al., 2005),
path planning (Tuffin, 1996). Many recent works
are concentrated on high dimension (Sloan and
Wo
´
zniakowski, 1998; Wasilkowski and Wozni-
akowski, 1997), with in particular successes when
the ”true” dimensionality of the underlying distri-
bution or domain is smaller than the apparent one
(Hickernell, 1998), or with scrambling-techniques
(L’Ecuyer and Lemieux, 2002).
• Low-dispersion optimization is similar, but uses
low-dispersion sequences (Niederreiter, 1992;
Lindemann and LaValle, 2003; LaValle et al.,
2004) instead of random i.i.d sequences ; low-
dispersion is related to low-discrepancy, but easier
to optimize. A dispersion-criterion is
Dispersion(P) = sup
x∈D
inf
p∈P
d(x, p) (2)
NONLINEAR PROGRAMMING IN APPROXIMATE DYNAMIC PROGRAMMING - Bang-bang Solutions,
Stock-management and Unsmooth Penalties
49

where d is the euclidean distance. It is related to
the following (easier to optimize) criterion (to be
maximized and not minimized):
Dispersion
2
(P) = inf
(x
1
,x
2
)∈D
2
d(x
1
,x
2
) (3)
we use eq. 3 in the sequel of this pa-
per. We optimize dispersion in a greedy man-
ner: each point x
n
is optimal for the disper-
sion of x
1
,...,x
n
conditionally to x
1
,...,x
n−1
;
i.e. x
1
= (0.5,0.5,...,0.5), x
2
is such that
Dispersion
2
({x
1
,x
2
}) is maximal, and x
n
is such
that Dispersion
2
({x
1
,...,x
n−1
,x
n
}) is minimal.
This sequence has the advantage of being much
faster to compute than the non-greedy one, and
that one does not need a priori knowledge of the
number of points. Of course, it is not optimal for
eq. 3 or eq. 2.
• Equation 3 pushes points on the frontier, what is
not the case in equation 2 ; therefore, we also
considered low-dispersion sequences ”far-from-
frontier”, where equation 3 is replaced by:
Dispersion
3
(P) = inf
(x
1
,x
2
)∈D
2
d(x
1
,{x
2
}∪D
′
) (4)
As for Dispersion
2
, we indeed used the greedy
and incremental counterpart of eq. 4.
• CMA-ES (EO and openBeagle implementation):
an evolution strategy with adaptive covariance
matrix (Hansen and Ostermeier, 1996; Keijzer
et al., 2001; Gagn
´
e, 2005).
• The Hooke & Jeeves (HJ) algorithm (Hooke and
Jeeves, 1961; Kaupe, 1963; Wright, 1995), avail-
able at
http://www.ici.ro/camo/unconstr/
hooke.htm
: a geometric local method imple-
mented in C by M.G. Johnson.
• a genetic algorithm (GA), from the sgLibrary
(
http://opendp.sourceforge.net
). It imple-
ments a very simple genetic algorithm where the
mutation is an isotropic Gaussian of standard de-
viation
σ
d
√
n
with n the number of individuals in
the population and d the dimension of space. The
crossover between two individuals x and y gives
birth to two individuals
1
3
x+
2
3
y and
2
3
x+
1
3
y. Let
λ
1
,λ
2
,λ
3
,λ
4
be such that λ
1
+ λ
2
+ λ
3
+ λ
4
= 1 ;
we define S
1
the set of the λ
1
.n best individuals,
S
2
the λ
2
.n best individuals among the others. At
each generation, the new offspring is (i) a copy
of S
1
(ii) nλ
2
cross-overs between individuals
from S
1
and individuals from S
2
(iii) nλ
3
mutated
copies of individuals from S
1
(iv) nλ
4
individuals
randomly drawn uniformly in the domain. The pa-
rameters are σ = 0.08,λ
1
= 1/10,λ
2
= 2/10,λ
3
=
3/10,λ
4
= 4/10; the population size is the square-
root of the number of fitness-evaluations allowed.
These parameters are standard ones from the li-
brary. We also use a ”no memory” (GANM) ver-
sion, that provides as solution the best point in the
final offspring, instead of the best visited point.
This is made in order to avoid choosing a point
from a narrow area of good fitness.
• limited-BFGS with finite differences, thanks to
the LBFGSB library (Zhu et al., 1994; Byrd
et al., 1995). Roughly speaking, LBFGS uses
an approximated Hessian in order to approximate
Newton-steps without the huge computational and
space cost associated to the use of a full Hessian.
In our experiments with restart, any optimization that
stops due to machine precision is restarted from a new
random (independent, uniform) point.
For algorithms based on an initial population, the
initial population is chosen randomly (uniformly, in-
dependently) in the domain. For algorithms based
on an initial point, the initial point is the middle
of the domain. For algorithms requiring step sizes,
the step size is the distance from the middle to the
frontier of the domain (for each direction). Other
parameters were chosen by the authors with equal
work for each method on a separate benchmark,
and then plugged in our dynamic programming tool.
The detailed parametrization is available in
http://
opendp.sourceforge.net
, with the command-line
generating tables of results.
Some other algorithms have been tested and re-
jected due to their huge computational cost: the DFO-
algorithm from Coin (Conn et al., 1997),
http://
www.coin-or.org/
; Cma-ES from Beagle (Hansen
and Ostermeier, 1996; Gagn
´
e, 2005) is similar to
Cma-ES from EO(Keijzer et al., 2001) and has also
been removed.
3 EXPERIMENTS
3.1 Experimental Settings
The characteristics of the problems are summarized
in table 1; problems are scalable and experiments
are performed with dimension (i) the baseline dimen-
sion in table 1 (ii) twice this dimensionality (iii) three
times (iv) four times. Both the state space dimen-
sion and the action space are multiplied. Results are
presented in tables below. The detailed experimental
setup is as follows: the learning of the function value
is performed by SVM with Laplacian-kernel (SVM-
Torch,(Collobert and Bengio, 2001)), with hyper-
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
50

parameters heuristically chosen; each optimizer is al-
lowed to use a given number of points (specified in ta-
bles of results); 300 points for learning are sampled in
a quasi-random manner for each time step, non-linear
optimizers are limited to 100 function-evaluations.
Each result is averaged among 66 runs. We can sum-
marize results below as follows. Experiments are per-
formed with:
• 2 algorithms for gradient-based methods (LBFGS
and LBFGS with restart),
• 3 algorithms for evolutionary algorithms (EO-
CMA, GeneticAlgorithm, GeneticAlgorithm-
NoMemory),
• 4 algorithms for best-of-a-predefined sample
(Low-Dispersion, Low-Dispersion ”fff”, Ran-
dom, Quasi-Random),
• 2 algorithms for pattern-search methods
(Hooke&Jeeves, Hooke&Jeeves with restart)
3.2 Results
Results varies from one benchmark to another. We
have a wide variety of benchmarks, and no clear su-
periority of one algorithm onto others arises. E.g.,
CMA is the best algorithm in some cases, and the
worst one in some others. One can consider that it
would be better to have a clear superiority of one and
only one algorithm, and therefore a clear conclusion.
Yet, it is better to have plenty of benchmarks, and as
a by-product of our experiments, we claim that con-
clusions extracted from one or two benchmarks, as
done in some papers, are unstable, in particular when
the benchmark has been adapted to the question under
study. The significance of each comparison (for one
particular benchmark) can be quantified and in most
cases we have sufficiently many experiments to make
results significant. But, this significance is for each
benchmark independently; in spite of the fact that we
have chosen a large set of benchmarks, coming from
robotics or industry, we can not conclude that the re-
sults could be extended to other benchmarks. How-
ever, some (relatively) stable conclusions are:
• For best-of-a-predefined-set-of-points:
– Quasi-random search is better than random
search in 17/20 experiments with very good
overall significance and close to random in the
3 remaining experiments.
– But low-dispersion, that is biased in the sense
that it ”fills” the frontier, is better in 10 on 20
benchmarks only; this is problem-dependent,
in the sense that in the ”away” or ”arm” prob-
lem, involving nearly bang-bang solutions (i.e.
best actions are often close to the boundary
for each action-variable) the Low-dispersion-
approach is often the best. LD is the best with
strong significance for many *-problems (in
which bang-bang solutions are reasonnable).
– And low-dispersion-fff, that is less biased, out-
performs random for 14 on 20 experiments (but
is far less impressive for bang-bang-problems).
• For order-2 techniques
2
: LBFGSB outperforms
quasi-random-optimization for 9/20 experiments;
Restart-LBFGSB outperforms quasi-random opti-
mization for 10/20 experiments. We suggest that
this is due to (i) the limited number of points (ii)
the non-convex nature of our problems (iii) the
cost of estimating a gradient by finite-differences
that are not in favor of such a method. Only
comparison-based tools were efficient. CMA is
a particular tool in the sense that it estimates a co-
variance (which is directly related to the Hessian),
but without computing gradients; a drawback is
that CMA is much more expensive (much more
computation-time per iterate) than other methods
(except BFGS sometimes). However it is some-
times very efficient, as being a good compromise
between a precise information (the covariance re-
lated to the Hessian) and fast gathering of in-
formation (no gradient computation). In partic-
ular, CMA was the best algorithm for all stock-
management problems (involving precise choices
of actions) as soon as the dimension is ≥ 8, with
in most cases strong statistical significance.
• The pattern-search method (the Hooke&Jeeves al-
gorithm with Restart) outperforms quasi-random
for 10 experiments on 20.
• For the evolutionary-algorithms:
– EoCMA outperforms Quasi-Random in 5/20
experiments. These 5 experiments are all stock-
management in high-dimension, and are often
very significant.
– GeneticAlgorithm outperforms Quasi-Random
in 14/20 experiments and Random in 17/20
experiments (with significance in most cases).
This algorithm is probably the most sta-
ble one in our experiments. GeneticAlgo-
rithmNoMemory outperforms Quasi-Random
in 14/20 experiments and Random in 15/20 ex-
periments.
Due to length-constraints, the detailed results,
for each method and with confidence intervals,
2
We include CMA in order-2 techniques in the sense that
it uses a covariance matrix which is strongly related to the
Hessian.
NONLINEAR PROGRAMMING IN APPROXIMATE DYNAMIC PROGRAMMING - Bang-bang Solutions,
Stock-management and Unsmooth Penalties
51

are reported to
http://www.lri.fr/
˜
teytaud/
sefordplong.pdf
. We summarize the results in ta-
ble 2.
4 CONCLUSION
We presented an experimental comparison of non lin-
ear optimization algorithms in the context of ADP.
The comparison involves evolutionary algorithms,
(quasi-)random search, discretizations, and pattern-
search-optimization. ADP has strong robustness re-
quirements, thus the use of evolutionary algorithms,
known for their robustness properties, is relevant.
These experiments are made in a neutral way; we
did not work more on a particular algorithm than
another. Of course, perhaps some algorithms re-
quire more work to become efficient on the prob-
lem. The reader can download our source code,
modify the conditions, check the parametrization,
and experiment himself. Therefore, our source code
is freely available at http://opendp.sourceforge.net
for further experiments. A Pascal-NoE challenge
(
www.pascal-network.org/Challenges/
) will be
launched soon so that anyone can propose his own al-
gorithms.
Our main claims are:
• High-dimensional stock-management. CMA-
ES is an efficient evolution-strategy when di-
mension increases and for ”less-unsmooth” prob-
lems. It is less robust than the GA, but ap-
pears as a very good compromise for the impor-
tant case of high-dimensional stock-management
problems. We do believe that CMA-ES, which
is very famous in evolution strategies, is in-
deed a very good candidate for non-linear opti-
mization as involved in high-dimensional-stock-
management where there is enough smoothness
for covariance-matrix-adaptation. LBFGS is not
satisfactory: in ADP, convexity or derivability are
not reliable assumptions, as explained in section
1.1, even if the law of increasing marginal cost
applies. Experiments have been performed with
dimension ranging from 4 to 16, without heuris-
tic dimension reduction or problem-rewriting in
smaller dimension, and results are statistically
clearly significant. However, we point out that
CMA-ES has a huge computational cost. The
algorithms are compared above in the case of
a given number of calls to the fitness; this is
only a good criterion when the computational
cost is mainly the fitness-evaluations. For very-
fast fitness-evaluations, CMA-ES might be pro-
hibitively too expensive.
• Robustness requirement in highly unsmooth
problems. Evolutionary techniques are the only
ones that outperform quasi-random-optimization
in a stable manner even in the case of very un-
smooth penalty-functions (see **-problems in the
Table 2). The GA is not always the best optimizer,
but in most cases it is at least better than random;
we do believe that the well-known robustness of
evolutionary algorithms, for the five meanings of
robustness pointed out in section 1.1, are fully rel-
evant for ADP.
• A natural tool for generating bang-bang-
efficient controlers. In some cases (typically
bang-bang problems) the LD-discretization intro-
ducing a bias towards the frontiers are (unsur-
prisingly) the best ones, but for other problems
LD leads to the worst results of all techniques
tested. This is not a trivial result, as this points out
LD as a natural way of generating nearly bang-
bang solutions, which depending on the number
of function-evaluations allowed, samples the mid-
dle of the action space, and then the corners, and
then covers the whole action space (what is proba-
bly a good ”anytime” behavior). A posteriori, LD
appears as a natural candidate for such problems,
but this was not so obvious a priori.
REFERENCES
Auger, A., Jebalia, M., and Teytaud, O. (2005). Xse: quasi-
random mutations for evolution strategies. In Pro-
ceedings of EA’2005, pages 12–21.
B
¨
ack, T., Hoffmeister, F., and Schwefel, H.-P. (1991). A
survey of evolution strategies. In Belew, R. K. and
Booker, L. B., editors, Proceedings of the 4
th
Interna-
tional Conference on Genetic Algorithms, pages 2–9.
Morgan Kaufmann.
B
¨
ack, T., Rudolph, G., and Schwefel, H.-P. (1993). Evolu-
tionary programming and evolution strategies: Simi-
larities and differences. In Fogel, D. B. and Atmar, W.,
editors, Proceedings of the 2
nd
Annual Conference on
Evolutionary Programming, pages 11–22. Evolution-
ary Programming Society.
B
¨
ack, T. and Sch
¨
utz, M. (1995). Evolution strategies for
mixed-integer optimization of optical multilayer sys-
tems. In McDonnell, J. R., Reynolds, R. G., and Fogel,
D. B., editors, Proceedings of the 4
th
Annual Confer-
ence on Evolutionary Programming. MIT Press.
Bertsekas, D. (1995). Dynamic Programming and Optimal
Control, vols I and II. Athena Scientific.
Bertsekas, D. and Tsitsiklis, J. (1996). Neuro-dynamic pro-
gramming, athena scientific.
Beyer, H.-G. (2001). The Theory of Evolutions Strategies.
Springer, Heidelberg.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
52

Beyer, H.-G., Olhofer, M., and Sendhoff, B. (2004). On the
impact of systematic noise on the evolutionary opti-
mization performance - a sphere model analysis, ge-
netic programming and evolvable machines, vol. 5,
no. 4, pp. 327 360.
Broyden., C. G. (1970). The convergence of a class of
double-rank minimization algorithms 2, the new algo-
rithm. j. of the inst. for math. and applications, 6:222-
231.
Byrd, R., Lu, P., Nocedal, J., and C.Zhu (1995). A limited
memory algorithm for bound constrained optimiza-
tion. SIAM J. Scientific Computing, vol.16, no.5.
Cervellera, C. and Muselli, M. (2003). A deterministic
learning approach based on discrepancy. In Proceed-
ings of WIRN’03, pp53-60.
Collobert, R. and Bengio, S. (2001). Svmtorch: Support
vector machines for large-scale regression problems.
Journal of Machine Learning Research, 1:143–160.
Conn, A., Scheinberg, K., and Toint, L. (1997). Re-
cent progress in unconstrained nonlinear optimization
without derivatives.
DeJong, K. A. (1992). Are genetic algorithms function op-
timizers ? In Manner, R. and Manderick, B., editors,
Proceedings of the 2
nd
Conference on Parallel Prob-
lems Solving from Nature, pages 3–13. North Holland.
Fitzpatrick, J. and Grefenstette, J. (1988). Genetic algo-
rithms in noisy environments, in machine learning:
Special issue on genetic algorithms, p. langley, ed.
dordrecht: Kluwer academic publishers, vol. 3, pp.
101 120.
Fletcher, R. (1970). A new approach to variable-metric al-
gorithms. computer journal, 13:317-322.
Gagn
´
e, C. (2005). Openbeagle 3.1.0-alpha.
Gelly, S., Ruette, S., and Teytaud, O. (2006). Comparison-
based algorithms: worst-case optimality, optimality
w.r.t a bayesian prior, the intraclass-variance mini-
mization in eda, and implementations with billiards.
In PPSN-BTP workshop.
Goldfarb, D. (1970). A family of variable-metric algorithms
derived by variational means. mathematics of compu-
tation, 24:23-26.
Hansen, N. and Ostermeier, A. (1996). Adapting arbi-
trary normal mutation distributions in evolution strate-
gies: The covariance matrix adaption. In Proc. of the
IEEE Conference on Evolutionary Computation (CEC
1996), pages 312–317. IEEE Press.
Hickernell, F. J. (1998). A generalized discrepancy and
quadrature error bound. Mathematics of Computation,
67(221):299–322.
Hooke, R. and Jeeves, T. A. (1961). Direct search solution
of numerical and statistical problems. Journal of the
ACM, Vol. 8, pp. 212-229.
Jin, Y. and Branke, J. (2005). Evolutionary optimization in
uncertain environments. a survey, ieee transactions on
evolutionary computation, vol. 9, no. 3, pp. 303 317.
Kaupe, A. F. (1963). Algorithm 178: direct search. Com-
mun. ACM, 6(6):313–314.
Keijzer, M., Merelo, J. J., Romero, G., and Schoenauer, M.
(2001). Evolving objects: A general purpose evolu-
tionary computation library. In Artificial Evolution,
pages 231–244.
LaValle, S. M., Branicky, M. S., and Lindemann, S. R.
(2004). On the relationship between classical grid
search and probabilistic roadmaps. I. J. Robotic Res.,
23(7-8):673–692.
L’Ecuyer, P. and Lemieux, C. (2002). Recent advances in
randomized quasi-monte carlo methods. pages 419–
474.
Lindemann, S. R. and LaValle, S. M. (2003). Incremen-
tal low-discrepancy lattice methods for motion plan-
ning. In Proceedings IEEE International Conference
on Robotics and Automation, pages 2920–2927.
Niederreiter, H. (1992). Random Number Generation and
Quasi-Monte Carlo Methods. SIAM.
Owen, A. (2003). Quasi-Monte Carlo Sampling, A Chapter
on QMC for a SIGGRAPH 2003 course.
Sendhoff, B., Beyer, H.-G., and Olhofer, M. (2004). The
influence of stochastic quality functions on evolution-
ary search, in recent advances in simulated evolution
and learning, ser. advances in natural computation, k.
tan, m. lim, x. yao, and l. wang, eds. world scientific,
pp 152-172.
Shanno, D. F. (1970.). Conditioning of quasi-newton meth-
ods for function minimization. mathematics of com-
putation, 24:647-656.
Sloan, I. and Wo
´
zniakowski, H. (1998). When are quasi-
Monte Carlo algorithms efficient for high dimensional
integrals? Journal of Complexity, 14(1):1–33.
Sutton, R. and Barto, A. (1998). Reinforcement learning:
An introduction. MIT Press., Cambridge, MA.
Tsutsui, S. (1999). A comparative study on the effects
of adding perturbations to phenotypic parameters in
genetic algorithms with a robust solution searching
scheme, in proceedings of the 1999 ieee system, man,
and cybernetics conference smc 99, vol. 3. ieee, pp.
585 591.
Tuffin, B. (1996). On the use of low discrepancy sequences
in monte carlo methods. In Technical Report 1060,
I.R.I.S.A.
Wasilkowski, G. and Wozniakowski, H. (1997). The expo-
nent of discrepancy is at most 1.4778. Math. Comp,
66:1125–1132.
Wright, M. (1995). Direct search methods: Once
scorned, now respectable. Numerical Analysis
(D. F. Griffiths and G. A. Watson, eds.), Pitman
Research Notes in Mathematics, pages 191–208.
http://citeseer.ist.psu.edu/wright95direct.html.
Zhu, C., Byrd, R., P.Lu, and Nocedal, J. (1994). L-BFGS-B:
a limited memory FORTRAN code for solving bound
constrained optimization problems. Technical Report,
EECS Department, Northwestern University.
NONLINEAR PROGRAMMING IN APPROXIMATE DYNAMIC PROGRAMMING - Bang-bang Solutions,
Stock-management and Unsmooth Penalties
53
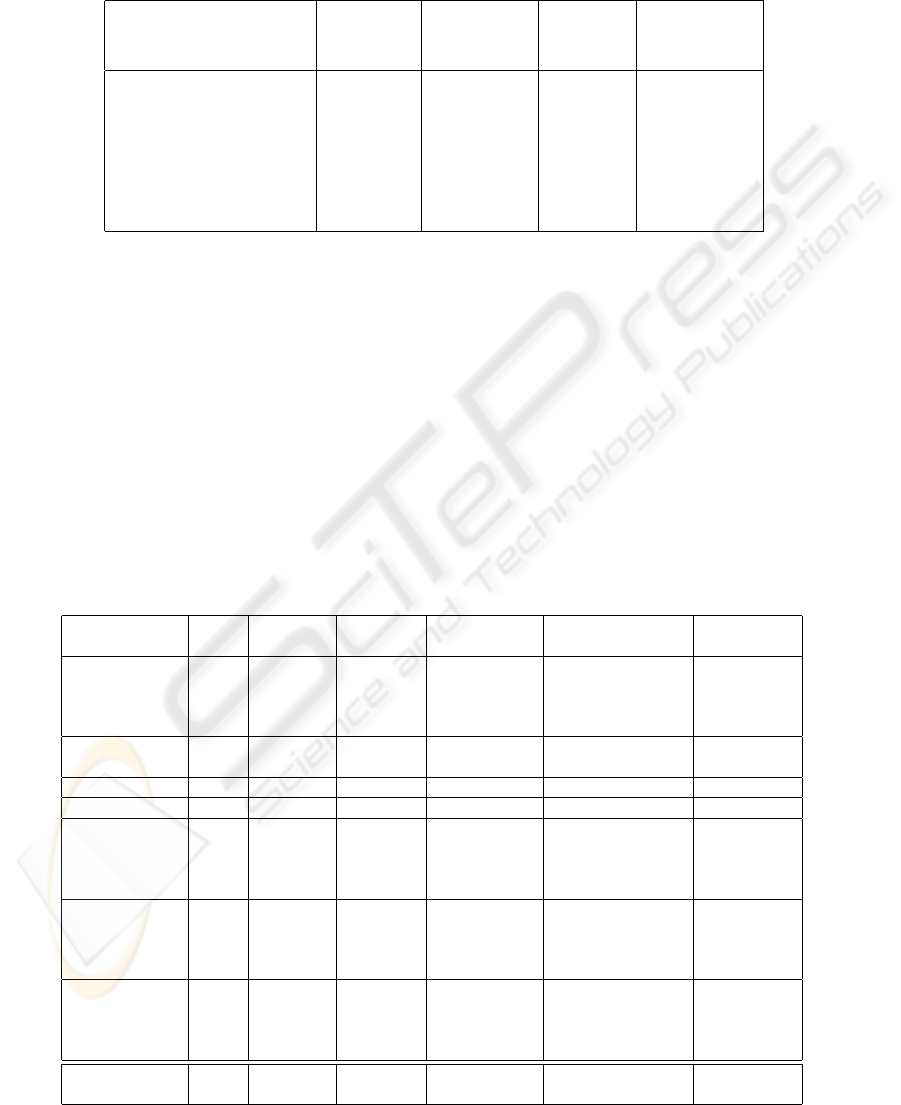
Table 1: Summary of the characteristics of the benchmarks. The stock management problems theoretically lead to convex
Bellman-functions, but their learnt counterparts are not convex. The ”arm” and ”away” problem deal with robot-hand-control;
these two problems can be handled approximately (but not exactly) by bang-bang solutions. Walls and Multi-Agent problems
are motion-control problems with hard penalties when hitting boundaries; the loss functions are very unsmooth.
Nb of State space Nb Action space
Name time steps dimension scenarios dimension
(basic case) (basic case)
Stock Management 30 4 9 4
Stock Management V2 30 4 9 4
Fast obstacle avoidance 20 2 0 1
Arm 30 3 50 3
Walls 20 2 0 1
Multi-agent 20 8 0 4
Away 40 2 2 2
Table 2: Experimental results. All stds are available at
http://www.lri.fr/
˜
teytaud/sefordplong.pdf
. For the ”best
algorithm” column, bold indicates 5% significance for the comparison with all other algorithms and italic indicates 5%
significance for the comparison with all but one other algorithms. y holds for 10%-significance. Detailed results in
http:
//www.lri.fr/
˜
teytaud/sefordplong.pdf
show that many comparisons are significant for larger families of algorithms,
e.g. if we group GA and GANM, or if we compare algorithms pairwise. Problems with a star are problems for which
bang-bang solutions are intuitively appealing; LD, which over-samples the frontiers, is a natural candidate for such problems.
Problems with two stars are problems for which strongly discontinuous penalties can occur; the first meaning of robustness
discussed in section 1.1 is fully relevant for these problems. Conclusions: 1. GA outperforms random and often QR. 2. For
*-problems with nearly bang-bang solutions, LD is significantly better than random and QR in all but one case, and it is the
best in 7 on 8 problems. It’s also in some cases the worst of all the tested techniques, and it outperforms random less often
than QR or GA. LD therefore appears as a natural efficient tool for generating nearly bang-bang solutions. 3. In **-problems,
GA and GANM are often the two best tools, with strong statistical significance; their robustness for various meanings cited in
section 1.1 make them robust solutions for solving non-convex and very unsmooth problems with ADP. 4. Stock management
problems (the two first problems) are very efficiently solved by CMA-ES, which is a good compromise between robustness
and high-dimensional-efficiency, as soon as dimensionality increases.
Problem Dim. Best QR beats GA beats LBFGSBrestart LD beats
algo. random random ; QR beats random;QR random;QR
Stock 4 LDfff y y;n y ; n y ; n
and 8 EoCMA y n;n n ; n n ; n
Demand 12 EoCMA y n;n n ; n n ; n
16 EoCMA n n;n n ; n n ; n
Stock and 4 LD y y;y y; y y; y
Demand2 8 EoCMA n y;y n ; y y ; y
Avoidance 1 HJ y y;n n ; n y; y
Walls** 1 GA y y;y y ; y y ; y
Multi-agent** 4 GA n y;y n ;n n ; n
8 GANM y y;y n ;n n ; n
12 LDfff y y;y n ;n n ; n
16 GANM y y;y n ;n y ; n
Arm* 3 LD y y;y y ; y y; y
6 HJ y y;y y ; y y; y
9 LD y y;n y ; y y; y
12 LD y y;y y ; y y; y
Away* 2 LD y y;y y ; n y; y
4 LD y y;y y ; y y; y
6 LD y y;y y ; y y; y
8 LD y y;y y ; y y; y
Total 17/20 17/20 ; 11/20 ; 14/20 ;
14/20 10/20 12/20
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
54
