CALIBRATION OF QUASI-ISOTROPIC PARALLEL

KINEMATIC MACHINES: ORTHOGLIDE

Anatoly Pashkevich, Roman Gomolitsky

Robotic Laboratory, Department of Control Systems

Belarusian State University of Informatics and Radioelectronics

6 P.Brovka St., Minsk 220027, Belarus

Philippe Wenger, Damien Chablat

Institut de Recherche en Communications et Cybernétique de Nantes

1, rue de la Noe B.P. 6597, 44321 Nantes Cedex 3, France

Keywords: Parallel robots, calibration, parameter identification, error compensation.

Abstract: The paper proposes a novel approach for the geometrical model calibr

ation of quasi-isotropic parallel

kinematic mechanisms of the Orthoglide family. It is based on the observations of the manipulator leg

parallelism during motions between the specific test postures and employs a low-cost measuring system

composed of standard comparator indicators attached to the universal magnetic stands. They are

sequentially used for measuring the deviation of the relevant leg location while the manipulator moves the

TCP along the Cartesian axes. Using the measured differences, the developed algorithm estimates the joint

offsets and the leg lengths that are treated as the most essential parameters. Validity of the proposed

calibration technique is confirmed by the experimental results.

1 INTRODUCTION

Parallel kinematic machines (PKM) are commonly

claimed as appealing solutions in many industrial

applications due to their inherent structural rigidity,

good payload-to-weight ratio, high dynamic

capacities and high accuracy (Tlusty et al., 1999;

Merlet, 2000; Wenger et al., 2001). However, while

the PKM usually exhibit a much better repeatability

compared to serial mechanisms, they may not

necessarily posses a better accuracy, which is

limited by manufacturing/assembling errors in

numerous links and passive joints (Wang and

Masory, 1993). Thus, the PKM accuracy highly

relies on the accurate kinematic model, which must

be carefully tuned for each manipulator separately.

Similar to the serial manipulators, the PKM

cal

ibration techniques are based on the minimization

of a parameter-dependent error function, which

incorporates residuals of the kinematic equations.

For the parallel manipulators, the inverse kinematic

equations are considered computationally more

efficient (contrary to the direct kinematics, which is

usually analytically unsolvable for the PKM)

(Innocenti, 1995; Iurascu & Park, 2003; Jeong et al.,

2004, Huang et al., 2005). But the main difficulty

with this technique is the full-pose measurement

requirement, which is very hard to implement

accurately. Hence, a number of studies have been

directed at using the subset of the pose measurement

data, which however creates another problem, the

identifiability of the model parameters.

Popular approaches in the parallel robot

cal

ibration deal with one-dimensional pose errors

using a double-ball-bar system or other measuring

devices, as well as imposing mechanical constraints

on some elements of the manipulator (Daney, 2003).

However, in spite of hypothetical simplicity, it is

hard to implement in practice since an accurate extra

mechanism is required to impose these constraints.

Additionally, such methods reduce the workspace

size and consequently the identification efficiency.

Another category of the methods, the self- or

tonomous calibration, is implemented by

Pashkevich A., Gomolitsky R., Wenger P. and Chablat D. (2007).

CALIBRATION OF QUASI-ISOTROPIC PARALLEL KINEMATIC MACHINES: ORTHOGLIDE.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 84-91

DOI: 10.5220/0001646000840091

 SciTePress

minimizing the residuals between the computed and

measured values of the active and/or redundant joint

sensors. Adding extra sensors at the usually

unmeasured joints is very attractive from

computational point of view, since it allows getting

the data in the whole workspace and potentially

reduces impact of the measurement noise. However,

only a partial set of the parameters may be identified

in this way, since the internal sensing is unable to

provide sufficient information for the robot end-

effector absolute location.

More recently, several hybrid calibration

methods were proposed that utilize intrinsic

properties of a particular parallel machine allowing

extracting the full set of the model parameters (or

the most essential of them) from a minimum set of

measurements. It worth mentioning an innovative

approach developed by Renaud et al. (2004, 2005)

who applied the vision-based measurement system

for the PKM calibration from the leg observations.

In this technique, the source data are extracted from

the leg images, without any strict assumptions on the

end-effector poses. The only assumption is related to

the manipulator architecture (the mechanism is

actuated by linear drives located on the base).

However, current accuracy of the camera-based

measurements is not high enough yet to apply this

method in industrial environment.

This paper extends our previous research

(Pashkevich et al., 2006) and focuses on the

calibration of the Orthoglide-type mechanisms,

which is also actuated by linear drives located on the

manipulator base and admits technique of Renaud et

al. (2004, 2005). But, in contrast to the known

works, our approach assumes that the leg location is

observed for specific manipulator postures, when the

tool-center-point moves along the Cartesian axes.

For these postures and for the nominal Orthoglide

geometry, the legs are strictly parallel to the

corresponding Cartesian planes. So, the deviation of

the manipulator parameters influences on the leg

parallelism that gives the source data for the

parameter identification. The main advantage of this

approach is the simplicity and low cost of the

measuring system that can avoid using computer

vision and is composed of standard comparator

indicators attached to the universal magnetic stands.

The remainder of the paper is organized as

follows. Section 2 describes the manipulator

geometry, its inverse and direct kinematics, and also

contains the sensitivity analysis of the leg

parallelism at the examined postures with respect to

the geometrical parameters. Section 3 focuses on the

parameter identification, with particular emphasis on

the calibration accuracy under the measurement

noise. Section 4 contains experimental results that

validate the proposed technique, while Section 5

summarizes the main contributions.

2 ORTHOGLIDE MECHANISM

2.1 Manipulator Architecture

The Orthoglide is a three degrees-of-freedom

parallel manipulator actuated by linear drives with

mutually orthogonal axes. Its kinematic architecture

is presented in Figure 1 and includes three identical

parallel chains, which will be further referred as

“legs”. Each manipulator leg is formally described

as PRP

R - chain, where P, R and P

denote the

prismatic, revolute, and parallelogram joints

respectively (Figure 2). The output machinery (with

a tool mounting flange) is connected to the legs in

such a manner that the tool moves in the Cartesian

space with fixed orientation (translational motions).

Figure 1: The Orthoglide kinematic architecture.

The Orthoglide workspace has a regular, quasi-

cubic shape. The input/output equations are simple

and the velocity transmission factors are equal to

one along the x, y and z direction at the isotropic

configuration, like in a conventional serial PPP

machine (Wenger et al., 2000; Chablat and Wenger,

2003). The latter is an essential advantage of the

Orthoglide architecture, which also allows referring

it as the “quasi-isotropic” kinematic machine.

Another specific feature of the Orthoglide

mechanism, which will be further used for the

calibration, is displayed during the end-effector

motions along the Cartesian axes. For example, for

the x-axis motion in the Cartesian space, the sides of

the x-leg parallelogram must also retain strictly

parallel to the x-axis. Hence, the observed deviation

CALIBRATION OF QUASI-ISOTROPIC PARALLEL KINEMATIC MACHINES: ORTHOGLIDE

of the mentioned parallelism may be used as the data

source for the calibration algorithms.

Figure 2: Kinematics of the Orthoglide leg.

For a small-scale Orthoglide prototype used for

the calibration experiments, the workspace size is

approximately equal to 200×200×200 mm

with the

velocity transmission factors bounded between 1/2

and 2 (Chablat & Wenger, 2003). The legs nominal

geometry is defined by the following parameters:

= 310.25 mm, d = 80 mm, r = 31 mm where L

, d

are the parallelogram length and width, and r is the

distance between the points Ci and the tool centre

point P (see Figure 2).

2.2 Modelling Assumptions

Following previous studies on the PKM accuracy

(Wang & Massory, 1993; Renaud et al., 2004), the

influence of the joint defects is assumed negligible

compared to the encoder offsets and the link length

deviations. This validates the following modelling

assumptions:

(i) the manipulator parts are supposed to be rigid

bodies connected by perfect joints;

(ii) the manipulator legs (composed of a prismatic

joint, a parallelogram, and two revolute joints)

generate a four degrees-of-freedom motions;

(iii) the articulated parallelograms are assumed to

be perfect but non-identical;

(iv) the linear actuator axes are mutually orthogonal

and intersected in a single point to insure a

translational movement of the end-effector;

(v) the actuator encoders are perfect but located

with some errors (offsets).

Using these assumptions, there will be derived

new calibration equations based on the observation

of the parallel motions of the manipulator legs.

2.3 Basic Equations

Since the kinematic parallelograms are admitted to

be non-identical, the kinematic model developed in

in our previous papers (Pashkevich et al., 2005,

2006) should be extended to describe the

manipulator with different length of the legs.

Under the adopted assumptions, similar to the

equal-leg case, the articulated parallelograms may be

replaced by the kinematically equivalent bar links.

Besides, a simple transformation of the Cartesian

coordinates (shift by the vector (r, r, r)

, see Figure

2) allows to eliminate the tool offset. Hence, the

Orthoglide geometry can be described by a

simplified model, which consists of three rigid links

connected by spherical joints to the tool centre point

(TCP) at one side and to the allied prismatic joints at

another side. Corresponding formal definition of

each leg can be presented as PSS, where P and S

denote the actuated prismatic joint and the passive

spherical joint respectively.

Thus, if the origin of a reference frame is located

at the intersection of the prismatic joint axes and the

x, y, z-axes are directed along them, the manipulator

kinematics may be described by the following

equations

⎥

⎦

⎤

⎢

⎣

⎡

−

++Δ+

xxx

xxxxx

βθ

βθρρ

sin

cossin

coscos)(

;

(1a)

⎥

⎦

⎤

⎢

⎣

⎡

++Δ+

−

yyy

yyyyy

βθ

βθρρ

cossin

coscos)(

sin

;

(1b)

⎥

⎦

⎤

⎢

⎣

⎡

++Δ+

−=

zzzzz

zzz

βθρρ

βθ

coscos)(

sin

cossin

(1c)

where

p = (p

, p

)

is the output vector of the TCP

position,

= (

)

is the input vector of the

prismatic joints variables, Δ

= (Δ

, Δ

)

the encoder offset vector, θ

, β

, i∈{x, y, z} are the

parallelogram orientation angles (internal variables),

and L

are the length of the corresponding leg.

After elimination of the internal variables θ

, β

the kinematic model (1) can be reduced to three

equations

(

)

222

)(

ikjiii

Lppp =++Δ+−

ρρ

(2)

which includes components of the input and output

vectors

p and

only. Here, the subscripts

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

},,{,, zyxkji ∈

kji

≠

are used in all

combinations, and the joint variables

are obeyed

the prescribed limits

maxmin

defined in

the control software (for the Orthoglide prototype,

min

= -100 mm and

max

= +60 mm).

It should be noted that, for the case

0=Δ=Δ=Δ

zyx

and , the

nominal ‘‘mechanical-zero’’ posture of the

manipulator corresponds to the Cartesian

coordinates

LLLL

zyx

===

= (0, 0, 0)

and to the joints variables

= (L, L, L). Moreover, in such posture, the x-, y-

and z-legs are oriented strictly parallel to the

corresponding Cartesian axes. But the joint offsets

and the leg length differences cause the deviation of

the “zero” TCP location and corresponding

deviation of the leg parallelism, which may be

measured and used for the calibration.

Hence, six parameters (Δ

, Δ

z ,

, L

)

define the manipulator geometry and are in the focus

of the proposed calibration technique.

2.4 Inverse and Direct Kinematics

The inverse kinematic relations are derived from the

equations (2) in a straightforward way and only

slightly differ from the “nominal” case:

ikjiiii

ppLsp

ρρ

Δ−−−+=

222

(3)

where s

, s

∈{ ±1} are the configuration indices

defined for the “nominal” geometry as the signs of

– p

, ρ

– p

, ρ

– p

, respectively. It is obvious

that expressions (3) give eight different solutions,

however the Orthoglide prototype assembling mode

and the joint limits reduce this set to a single case

corresponding to the s

= s

= 1.

For the direct kinematics, equations (2) can be

subtracted pair-to-pair that gives linear relations

between the unknowns p

, p

, which may be

expressed in the parametric form as

)(22

ρρρρ

ρρ

Δ+

−

Δ+

(4)

where t is an auxiliary scalar variable. This reduces

the direct kinematics to the solution of a quadratic

equation with the coefficients

=++ CBtAt

;)()(

∑

≠

Δ+Δ+=

jjii

ρρρρ

sinα

cos

cosα

(a)

: XMax posture

(b)

: Zero

posture

sinα

cos

cosα

(c)

: XMin

posture

Figure 3: Specific postures of the Orthoglide (for the x-leg

motion along the Cartesian axis X).

;)()()(

2222

kkjj

kji

ρρρρρρ

Δ+Δ+−Δ+=

∑

∏

≠≠

4/)()(

24/)()(

224

222

kkjj

kji

iii

ρρρρ

Δ+Δ++

⎟

⎠

⎞

⎜

⎝

⎛

−Δ+⋅Δ+=

∑

∑∑

∏

≠≠

where

},,{,, zyxkji

∈

. From two possible solutions

that gives the quadratic formula, the Orthoglide

prototype (see Figure 1) admit a single one

AACBBt 2/)4(

−+−=

corresponding to the

manipulator assembling mode.

CALIBRATION OF QUASI-ISOTROPIC PARALLEL KINEMATIC MACHINES: ORTHOGLIDE

2.5 Differential Relations

To obtain the calibration equations, first let us derive

the differential relations for the TCP deviation for

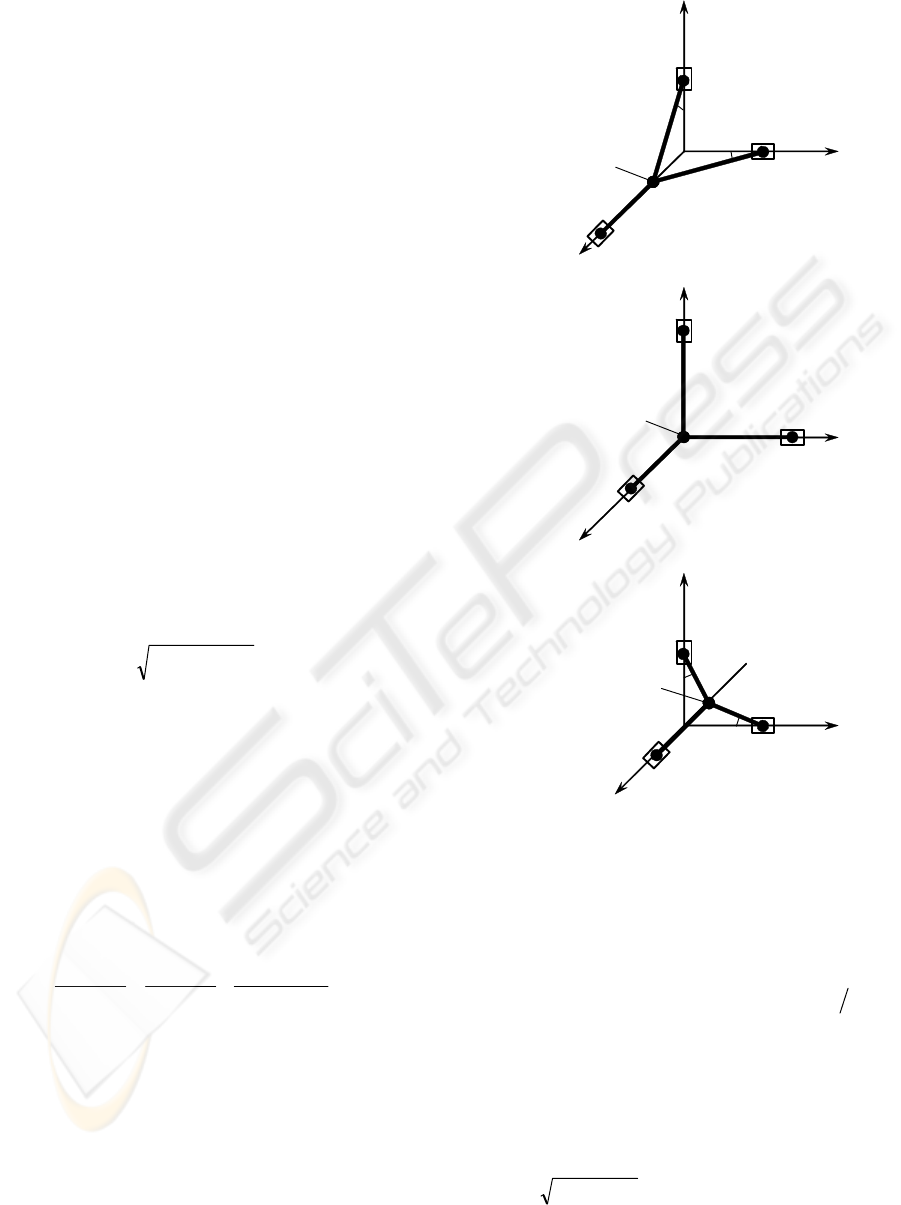
three types of the Orthoglide postures:

(i) “maximum displacement” postures for the

directions x, y, z (Figure 3a);

(ii) “mechanical zero” or the isotropic posture

(Figure 3b);

(iii) “minimum displacement” postures for the

directions x, y, z (Figure 3c);

These postures are of particular interest for the

calibration since, in the “nominal” case, a

corresponding leg is parallel to the relevant pair of

the Cartesian planes.

The manipulator Jacobian with respect to the

parameters Δ

=(Δ

, Δ

) and L = (

, L

)

can be derived by straightforward differentiating of

the kinematic equations (2), which yields

⎥

⎦

⎤

⎢

⎣

⎡

−

∂

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

zzyx

zyyx

zyxx

ρp

ρppp

pρpp

ppρp

⎥

⎦

⎤

⎢

⎣

⎡

∂

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

zzyx

zyyx

zyxx

ρppp

pρpp

ppρp

Thus, after the matrix inversions and

multiplications, the desired Jacobian can be written

[]

),();,(),( ρpJρpJρpJ

(5)

where

(.)

−

⎥

⎦

⎤

⎢

⎣

⎡

−−

ρp

(.)

−

⎥

⎦

⎤

⎢

⎣

⎡

−

ρp

It should be noted that, for the computing

convenience, the above expression includes both the

Cartesian coordinates p

, p

and the joint

coordinates

, but only one of these sets may

be treated as an independent taking into account the

inverse/direct kinematic relations.

For the “Zero” posture, the differential relations

are derived in the neighbourhood of the point

= (0, 0, 0) ; ρ

= (L, L, L)}, which after

substitution to (5) gives the Jacobian matrix

⎥

⎦

⎤

⎢

⎣

⎡

−

100100

010010

001001

(6)

Hence, in this case, the TCP displacement is related

to the joint offsets and the leg legs variations ΔL

trivial equations

;

iii

−

},,{ zyxi ∈

(7)

For the “XMax” posture, the Jacobian is

computed in the neighbourhood of the point

{

)0,0,(

;

),,(

ααα

LCLCLSL

}, where

α is the angle between the y-, z-legs and the X-

axes:

)/sin(

max

;

)(sin

)cos(

This gives the Jacobian

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

−+

010

001

001001

ααα

CTT

(8)

where

)tan(

. Hence, the desired equations

for the TCP displacement may be written as

xxx

Lp Δ

−

yxyxy

LCLTTp Δ−Δ−Δ+Δ=Δ

−1

ααα

ρρ

zxzxz

LCLTTp Δ−Δ−Δ+Δ=Δ

−1

ααα

ρρ

(9)

It can be proved that similar results are valid for the

“YMax” and “ZMax” postures (differing by the indices

only), and also for the “XMin”, “YMin”, “ZMin” postures.

In the latter case, the angle α should be computed

)/sin(

min

3 CALIBRATION METHOD

3.1 Measurement Technique

To evaluate the leg/surface parallelism, we propose

a single-sensor measurement technique. It is based

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

on the fixed location of the measuring device for two

distinct leg postures corresponding to the

minimum/maximum values of the joint coordinates

(Figure 4). Relevant calibration experiment consists

of the following steps:

Step 1. Move the manipulator to the “Zero”

posture; locate two gauges in the middle of the

X-leg (parallel to the axes Y and Z); get their

readings.

Step 2. Move the manipulator to the “XMax” and

“XMin” postures, get the gauge readings, and

compute differences.

Step 3+. Repeat steps 1, 2 for the Y- and Z-legs

and compute corresponding differences.

Manipulator legs

Δ = d

Manipulator legs

Base plane

Posture #1

Posture #2

Figure 4: Measuring the leg/surface parallelism.

3.2 Calibration Equations

The system of calibration equations can be derived

in two steps. First, it is required to define the gauge

initial locations that are assumed to be positioned at

the leg middle at the “Zero” posture, i.e. at the points

, where the vectors

2/)(

rp +

},,{ zyxi ∈

define

the prismatic joints centres:

)0;0;(

Δ+=r

;

)0;;0(

Δ+=r

);0;0(

Δ+=r

Hence, using the equation (7), the gauge initial

locations can be expressed as

⎟

⎠

⎞

⎜

⎝

⎛

Δ−Δ

Δ+

Δ−

;

⎟

⎠

⎞

⎜

⎝

⎛

Δ−Δ

Δ+

Δ−

Δ−Δ

;

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

Δ−

Δ−Δ

;

Afterwards, in the “XMax”, “YMax”, “ZMax”

postures, the leg location is also defined by two

points, namely, (i) the TCP, and (ii) the centre of the

prismatic joint

. For example, for the “XMax”

posture, the TCP position is

);;(

max

∗∗Δ−Δ+=

and the joint position is

)0;0;(

max

LSL

Δ++=r

So, the leg is located along the line

maxmax

)1()(

rps ⋅−+⋅=

μμμ

where μ is a scalar parameter, μ∈[0, 1]. Since the x-

coordinate of the gauge is independent of the

posture, the parameter μ may be obtained from the

equation

]

[)]([ gs =

, which solution yields:

LSS /5.0 Δ⋅

−

αα

Hence, after some transformations, the deviations of

the X-leg measurements (between the “XMax” and

“Zero” postures) may be expressed as

LCS

LTS

Δ−

−

+−Δ+−

−Δ+Δ+=

)5.0

)5.0(()5.0(

)5.0(

αααα

αα

LCS

LTS

Δ−

−

+−Δ+−

−Δ+Δ+=

)5.0

)5.0(()5.0(

)5.0(

αααα

αα

Similar approach may be applied to the “XMin”

posture, as well as to the corresponding postures for

the Y- and Z-legs. This gives the system of twelve

linear equations in six unknowns:

CALIBRATION OF QUASI-ISOTROPIC PARALLEL KINEMATIC MACHINES: ORTHOGLIDE

11 1 1

22 2 2

11 1 1

22 2 2

1111

111 1

2222

ab c b

ba b c

ab c b

ba b c

ab c b

ba b c

ab c b L

ba b c

abcb

bab c

abcb

babc

−−

⎡⎤

⎢⎥

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

−− Δ

⎢⎥

−− Δ

⎢⎥

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

⎣⎦

−

⎡⎤

⎢⎥

⎡⎤

⎢⎥

⎢

⎢⎥

⎣⎦

⎢⎥

⎣⎦

⎥

(10)

where

, ,

TSb

αα

+= )5.0(

5.0)5.0(

−+=

−

CSc

αα

and ,

0)/(asin

max1

>ρ=α L 0)/(asin

min2

ρ=α L

This system can be solved using the

pseudoinverse of Moore-Penrose, which ensures the

minimum of the residual square sum.

4 EXPERIMENTAL RESULTS

The measuring system is composed of standard

comparator indicators attached to the universal

magnetic stands allowing fixing them on the

manipulator bases. The indicators have resolution of

10 μm and are sequentially used for measuring the

X-, Y-, and Z-leg parallelism while the manipulator

moves between the Max, Min and Zero postures. For

each measurement, the indicators are located on the

mechanism base in such manner that a

corresponding leg is admissible for the gauge

contact for all intermediate postures (Figure 5).

For each leg, the measurements were repeated

three times for the following sequence of motions:

Zero → Max → Min → Zero→ …. Then, the results

were averaged and used for the parameter

identification (the repeatability of the measurements

is about 0.02 mm).

To validate the developed calibration technique

and the adopted modelling assumptions, there were

carried out three experiments targeted to the

following objectives: (#1) validation of modelling

assumptions; (#2) collecting the experimental data

for the parameter identification; and (#3) verification

of the calibration results.

Figure 5: Experimental Setup.

Table 1: Calibration results.

Parameters (mm)

ΔL

R.m.s.

(mm)

4.66 -5.36 1.46 5.20 -5.96 3.16 0.12

-0.48 0.49 -1.67 – – – 0.14

– – – 0.50 -0.52 1.69 0.14

The first experiment produced rather high

parallelism deviation, which impels to conclude that

the mechanism mechanics requires more careful

tuning. Consequently, the location of the joint axes

was adjusted mechanically to ensure the leg

parallelism for the Zero posture.

The second experiment (after mechanical tuning)

yielded lower deviations, twice better than for the

first experiment. For these data, the developed

calibration algorithm was applied for three sets of

the model parameters: for the full set {Δρ, Δ

L} and

for the reduced sets {Δρ} and {Δ

L}. As follows

from the identification results (Table 1), the

algorithms is able to identify simultaneously both

the joint offsets and Δρ and the link lengths Δ

However, both Δρ and Δ

L (separately) demonstrate

roughly the same influence on the residual

reduction, from 0.32 mm to 0.14 mm, while the full

set {Δρ, Δ

L} gives further residual reduction to the

0.12 mm only. This motivates considering Δρ as the

most essential parameters to be calibrated.

Accordingly, the identified vales of the joint offsets

were input into the control software.

The third experiment demonstrated good

agreement with the expected results. In particular,

the average deviation reduced down to 0.15 mm,

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

which corresponds to the measurement accuracy. On

the other hand, further adjusting of the model to the

new experimental data does not give the residual

reduction.

Hence, the calibration results confirm validity of

the proposed identification technique and its ability

to tune the joint offsets and link lengths from

observations of the leg parallelism. Other conclusion

is related to the modelling assumption: for further

accuracy improvement it is prudent to generalize the

manipulator model by including parameters

describing the orientation of the prismatic joint axes,

i.e. relaxing assumption (iv) (see sub-section 2.2).

5 CONCLUSIONS

This paper proposes further developments for a

novel calibration approach for parallel manipulators,

which is based on observations of manipulator leg

parallelism with respect to some predefined planes.

This technique employs a simple and low-cost

measuring system composed of standard comparator

indicators, which are sequentially used for

measuring the deviation of the relevant leg location

while the manipulator moves the TCP along the

Cartesian axes. From the measured differences, the

calibration algorithm estimates the joint offsets and

the link lengths that are treated as the most essential

parameters to be tuned. The validity of the proposed

approach and efficiency of the developed numerical

algorithm were confirmed by the calibration

experiments with the Orthoglide prototype, which

allowed essential reduction of the residuals and

corresponding improvement of the accuracy.

Future work will focus on the expanding the set of

the identified model parameters, their identifiably

analysis, and compensation of the non-geometric

errors.

REFERENCES

Chablat, D., Wenger, Ph., 2003. Architecture Optimization

of a 3-DOF Parallel Mechanism for Machining

Applications, the Orthoglide. IEEE Transactions On

Robotics and Automation, Vol. 19 (3), pp. 403-410.

Daney, D., 2003. Kinematic Calibration of the Gough

platform. Robotica, 21(6), pp. 677-690.

Huang, T., Chetwynd, D.G. Whitehouse, D.J., Wang, J.,

2005. A general and novel approach for parameter

identification of 6-dof parallel kinematic machines.

Mechanism and Machine Theory, Vol. 40 (2), pp. 219-

239.

Innocenti, C., 1995. Algorithms for kinematic calibration

of fully-parallel manipulators. In: Computational

Kinematics, Kluwer Academic Publishers, pp. 241-

250.

Iurascu, C.C. Park, F.C., 2003. Geometric algorithm for

kinematic calibration of robots containing closed

loops. ASME Journal of Mechanical Design, Vol.

125(1), pp. 23-32.

Jeong J., Kang, D., Cho, Y.M., Kim, J., 2004. Kinematic

calibration of redundantly actuated parallel

mechanisms. ASME Journal of Mechanical Design,

Vol. 126 (2), pp. 307-318.

Merlet, J.-P., 2000. Parallel Robots, Kluwer Academic

Publishers, Dordrecht, 2000.

Pashkevich, A., Wenger, P., Chablat, D., 2005. Design

Strategies for the Geometric Synthesis of Orthoglide-

type Mechanisms. Mechanism and Machine Theory,

Vol. 40 (8), pp. 907-930.

Pashkevich A., Chablat D., Wenger P., 2006. Kinematic

Calibration of Orthoglide-Type Mechanisms.

Proceedings of IFAC Symposium on Information

Control Problems in Manufacturing (INCOM’2006),

Saint Etienne, France, 17-19 May, 2006, p. 151 - 156

Renaud, P., Andreff, N., Pierrot, F., Martinet, P., 2004.

Combining end-effector and legs observation for

kinematic calibration of parallel mechanisms. IEEE

International Conference on Robotics and Automation

(ICRA’2004), New-Orleans, USA, pp. 4116-4121.

Renaud, P., Andreff, N., Martinet, P., Gogu, G., 2005.

Kinematic calibration of parallel mechanisms: a novel

approach using legs observation. IEEE Transactions

on Robotics and Automation, 21 (4), pp. 529-538.

Tlusty, J., Ziegert, J.C., Ridgeway, S., 1999. Fundamental

Comparison of the Use of Serial and Parallel

Kinematics for Machine Tools. CIRP Annals, Vol. 48

(1), pp. 351-356.

Wang, J. Masory, O. 1993. On the accuracy of a Stewart

platform - Part I: The effect of manufacturing

tolerances. IEEE International Conference on

Robotics and Automation (ICRA’93), Atlanta,

Georgia, pp. 114–120.

Wenger, P., Gosselin, C., Chablat, D., 2001. Comparative

study of parallel kinematic architectures for machining

applications. In: Workshop on Computational

Kinematics, Seoul, Korea, pp. 249-258.

Wenger, P., Gosselin, C. Maille, B., 1999. A comparative

study of serial and parallel mechanism topologies for

machine tools. In: Proceedings of PKM’99, Milan,

Italy, pp. 23–32.

CALIBRATION OF QUASI-ISOTROPIC PARALLEL KINEMATIC MACHINES: ORTHOGLIDE