HYBRID MOTION CUEING ALGORITHMS FOR REDUNDANT

ADVANCED DRIVING SIMULATORS

Hatem Elloumi, Nadia Ma

ızi and Marc Bordier

Centre de Math

ematiques Appliqu

ees,

Ecole des Mines de Paris

2004 route des Lucioles, 06902 Sophia Antipolis Cedex, France

Keywords:

Driving simulation, motion cueing, hybrid control.

Abstract:

Redundant Advanced Driving Simulators (hexapods mounted on rails) present an extra capability to reproduce

motion sensations. The exploitation of this capability is currently done by frequency separation methods with-

out taking into account the frequency overlapping between the hexapod and the rails. Within this bandwidth,

these two degrees of freedom could be considered as equivalent. Our aim is to use this equivalence to improve

the motion restitution. We offer two algorithms based on the hybrid systems framework which deal with the

longitudinal mode. Their goal is to improve the restitution of motion sensations by reducing false cues (gen-

erated by actuators braking) and decreasing null cues (due to actuators blocking). Our algorithms include and

treat all steps of motion cueing: motion tracking (restitution), braking before reaching the displacement limits,

washout motion, and switching rules.

1 INTRODUCTION

Driving simulators are advanced devices composed of

four components: a virtual scene projected on a wide

screen to imitate the road and the trafﬁc, an audio sys-

tem to play the driving sounds (horn, squeal of brakes,

etc.), a car cockpit (including a real dashboard, the

pedals and the seat of the driver) to copy the body

position and the interaction of the driver with a real

vehicle and ﬁnally a robot carrying the car cockpit to

provide its motion. While the ﬁrst three components

could be considered as offering a sufﬁciently high de-

gree of realism, the robot presents a very low capacity

of displacement, thus preventing it from performing

the real car motions.

In fact, the aim of a driving simulator is not

tracking real trajectories produced by outdoors driv-

ing but reproducing the corresponding motion sen-

sations. How could we then, generate realistic mo-

tion sensations in simulation despite the constrained

robot motion? It is the aim of Motion Cueing Algo-

rithms (MCA) to give heuristically an answer to this

problem. This paper uses the hybrid systems frame-

work (Zaytoon, 2001; Van der Shaft and Schumacher,

1999) to build two MCA designed speciﬁcally for re-

dundant simulation robots. These robots are made up

of two parts:

• A Gough-Stewart parallel robot or hexapod (this

parallel robot is composed of three parts: a mov-

ing body called the platfom (carrying the car cock-

pit) linked to the base through six extensible legs.

Each leg is composed of a prismatic joint (i.e. an

electro hydraulic jack) and two passive spherical

joints making the connection with the base and

the platform. For an excellent overview of parallel

robots the reader is referred (Merlet, 2000)). The

jacks’ excursions are of ±20cm allowing a six-

dimension motion of the car cockpit up to ±15cm

(in linear directions) and up to 30deg (for rota-

tions).

• A rail system carrying the base of the hexapod to

provide an extra motion in the horizontal plane. In

this paper the rails’ limits are: ±2m.

(Elloumi, 2006) shows that rails and the hexapod

present overlapping bandwidths in the high frequency

domain. So how could we beneﬁt from this redun-

dancy? Our approach is based on the classical MCA

which will be presented in section 3. But before ad-

dressing this point, section 2 will deal with the notion

209

Elloumi H., Maïzi N. and Bordier M. (2007).

HYBRID MOTION CUEING ALGORITHMS FOR REDUNDANT ADVANCED DRIVING SIMULATORS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 209-216

DOI: 10.5220/0001650102090216

 SciTePress

surge

pitch

surge

pitch

Figure 1: The longitudinal mode.

of sensation to close the description of the simulator

objective.

Remark: The results presented here are done for

the longitudinal mode. However, they could be ex-

tended for the other space directions. The longitudi-

nal mode is composed of the surge and pitch motions

as depicted in ﬁgure 1.

2 MOTION PERCEPTION

Even in the absence of visual information (closed-eye

subject), humans detect motion thanks to their inertial

receptor: the vestibular system. Located in the inner

ear, this biological apparatus measures both linear and

angular motion of the head (a thorough description is

given in (Elloumi, 2006; Telban et al., 2000; Ange-

laki and Dickman, 2004)) if they are beyond detection

thresholds (on acceleration and speed respectively).

The motion sensation is built at the level of the

brain not only from the vestibular system informa-

tion but also from all the perception receptors (most

particularly: the eyes) cues. In this paper, as com-

monly done in driving simulation, we consider that

apart from the vestibular system, all the other sensors

receive coherent and well adapted cues. As a conse-

quence, in this paper the motion sensation will be con-

sidered as the interpretation of head displacements by

the inertial receptor.

One remarkable gain of working with motion sen-

sations instead of real trajectories (accelerations) is il-

lustrated by the tilt coordination. In driving (or ﬂight)

simulation, a simultaneous rotation of the driver’s

head and the visual scene at a very slow rate happens

to create an illusion of linear acceleration: ”When a

visual scene representing an accelerated translation

is presented to the driver while the simulation cockpit

is tilted at an undetectable rate, the relative variation

of the gravity vector will be partly interpreted as an

actual linear acceleration” (Reymond et al., 2002).

Thus from a control point of view, the tilt coordination

leads to a low-frequency motion sensation through a

very small variation of the jacks’ displacement as we

shall see in the next section.

Scaling Saturation

High Frequency

Filtering

real

acceleration

treated

acceleration

Scaling Saturation

High Frequency

Filtering

real

acceleration

treated

acceleration

Figure 2: Preliminary treatments for the classical MCA.

3 CLASSICAL MOTION CUEING

ALGORITHM

This scheme was developed in 1970 by (Parrish et al.,

1975). Despite its simplicity, this algorithm displays

the importance of tilt coordination to restitute longitu-

dinal accelerations. This scheme is based on the sim-

ple observation that the simulator translation is very

limited so that only fast (onset) accelerations could be

tracked. Consequently, the principle of this method is

to use ﬁltering to extract from the real car accelera-

tion the high frequency component and address it to

the robot translation. Hopefully, the tilt coordination

enables the reproduction of slow (sustained) accelera-

tions. Filtering (low frequencies) is performed to sup-

ply the tilt rotation as well. As for the restitution of

the rotation speed, high pass ﬁltering is performed to

deal with angular limits.

The classical MCA is a linear approach which is

commonly preceded by some preliminary treatments

of the real accelerations to cope with robot motion

limits (see ﬁgure 2).

4 THE REDUNDANCY PROBLEM

Restituting longitudinal acceleration on redundant

simulators could be done thanks to three degrees of

freedom (dof) as depicted in Fig.3: the base transla-

tion (X) (performed by the rails), the hexapod trans-

lation (x) and the tilt coordination (θ : tilt angle)

(both performed by the jacks). As shown in (Elloumi,

2006), the behavior of the last dof is independent from

the ﬁrst two as the rotation due to the tilting is limited

by a very low detection threshold.

As a consequence, in order to improve the qual-

ity of motion cueing only the translations behaviors

should be considered. The considered linear acceler-

ation

provided to the driver by the simulation robot

is then:

X + ¨x .

Besides as the rails and jacks bandwidths are over-

lapping in the high frequencies domain, these two dof

could be considered as equivalent. How could we

The tilt coordination contribution gθ (where g is the

gravity magnitude) is omitted from the hybrid algorithms

that we shall present (but could be added outside these al-

gorithms).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

210

then exploit this equivalence? We offer two algo-

rithms based on the hybrid systems framework which

use only one translation at a time and a switching

strategy to cope with the limits.

Figure 3 shows these two translations: hexapod

translation (x) and base translation (X) each con-

strained by three levels of limitation: position, speed

and acceleration ±ξ

, ±

(ξ ∈ {x, X}). The

models ruling the variation of ξ ∈ {x, X} are lin-

earized models (double integrators):

ξ = u

, ξ ∈ {x, X} (1)

where u

is the reference acceleration (control). As

these dof are limited, we have to deﬁne two strate-

gies: a braking strategy (triggered when nearing the

limits) and a washout strategy (going back to a neu-

tral position) strategy (once braking has been done).

4.1 Braking Strategy

In this paper we adopted the parabolic braking (con-

stant braking acceleration

) in order to stop the

translation at its limits ±ξ

(null speed

ξ = 0). The

triggering condition is then:

− 2

(ξ

− |ξ|) ≥ 0, ξ ∈ {x, X} (2)

The braking acceleration

determines the free zone

(braking-free zone) size. The higher

is the bigger

is the free zone. Nevertheless, the incoherent sensa-

tions would be strong in this case. At the opposite,

choosing this acceleration to be as low as the detec-

tion threshold (0.05ms

−2

) would considerably reduce

the braking sensations and would noticeably reduce

the free zone at the same time.

We have studied the inﬂuence of this parameter on

the ratio between the free zone volume and the theo-

retically available one. As the phase proﬁle (speed

and position) is independent from the acceleration

value, this ratio is equal to the ratio between the sur-

faces of the phase proﬁles. The theoretical surface is

theo

= 4ξ

and the free zone surface is:

free







if 0 ≤

−

−1

otherwise

(3)

The ratio S

free

theo

is saturated starting from a cer-

tain braking acceleration

. In other words, starting

from this point, the magnitude of

wouldn’t have

a signiﬁcant impact on the free zone size. However,

the braking duration

−1

(bounded by

−1

) will

keep decreasing.

4.2 Washout Strategies

The goal of the washout is to bring the translation to

its neutral position (ξ,

ξ) = (0, 0). We present two

washout strategies:

4.2.1 Known Starting Point

In this case the backward motion starts at (ξ,

ξ) =

(±ξ

, 0), the chosen washout control is:

= −sign(ξ)



≤ |ξ| ≤ ξ

−a

if 0 ≤ |ξ| ≤

(4)

Taking a

= a

threshold

= 0.05ms

−2

would make

this motion imperceptible. Finally, the duration of this

strategy is: 2

−1

4.2.2 Unknown Starting Point

In this case the backward motion starts at an unknown

point (within the limits). The control is then a Propor-

tional Derivative (PD):

ξ = −µ

ξ − kξ (5)

The parameters (µ, k) have to be chosen so that the

motion limits are respected.

These deﬁnitions of braking and washout tech-

niques enable us to present our hybrid algorithms.

5 SYMMETRIC ALGORITHM

The principle of the symmetric algorithm is to use

only one translation at a time. When the active trans-

lation reaches its limits, switching will be performed

to activate the idle dof. In other words, both trans-

lations reproduce the reference acceleration as relay

runners.

In non redundant simulators (without rails), when

the hexapod translation is close to its limits, braking

and washout will be successively triggered. The op-

erator has to wait until these two operations ﬁnish in

order to get back coherent motion cues. The symmet-

ric algorithm will speed up the reactivation of the ac-

celeration restitution by using the idle translation dur-

ing the washout (impercebtible) motion of the active

one. This algorithm is called symmetric because both

translations have the same role in the motion cueing

process.

In order to represent the symmetric algorithm as a

hybrid automaton, two points have to be deﬁned: the

working modes and the rules of correct operation.

HYBRID MOTION CUEING ALGORITHMS FOR REDUNDANT ADVANCED DRIVING SIMULATORS

211

tilt coordination hexapod translation base translationtilt coordinationtilt coordination hexapod translationhexapod translation base translationbase translation

Figure 3: The redundancy of the longitudinal acceleration restitution.

Working Modes

In the case of the symmetric algorithm, both transla-

tions (X and x) have the same working modes:

1. active: the dof ξ tracks the treated reference ac-

celeration

2. brake: parabolic braking

3. washout: known starting point

4. idle: null acceleration

Rules of Correct Operation

By deﬁning these rules we characterize the way the

hybrid automaton works. In our case, these rules are

valid for both translations:

1. braking must lead to the limit position with a null

speed

2. braking must be followed by a washout motion

3. washout must lead to the neutral position with a

null speed

4. reactivating one dof could be done only starting

from the neutral position (with a null speed)

5. if one dof is braking, the other one mustn’t be ac-

tive. The braking sensations could deteriorate in-

deed the quality of the free dof restitution

5.1 The Symmetric Automaton

Figure 4 shows the symmetric automaton (we ob-

serve a central symmetry around the state (Hexapod:

washout, Rail: washout)). Three types of transition

predicates appear:

• hexa=0 (or rail=0) i.e. the dof has attained

the neutral position (ξ,

ξ) = (0, 0)

• decl

hexa (or decl rail) i.e. the braking

condition is fulﬁlled (see (2))

• lim

hexa (or lim rail) i.e. that an extreme

position (ξ,

ξ) = (±ξ

, 0) has been attained

If we consider that braking is instantaneous then this

automaton could be reduced to the four states outside

the dashed box i.e. an alternation between the activa-

tion and the washout for both translations. The states

inside the box take into account the parabolic braking

and the subsequent activation of the washout.

5.2 Simulations

Matlab/Simulink and Stateﬂow were used to perform

simulations. The initial state was chosen to be (Rail:

active, Hexapod: idle). The reference acceleration

proﬁle was extracted from the Renault simulations

in (Dagdelen, 2005). The parameters values used in

these simulations are :

= 1ms

−2

, ¨x

= 0.2ms

−2

and a

= 0.05ms

−2

for both dof. Transition times

are indicated by vertical lines. In ﬁgure 5, we can dis-

tinguish 6 working phases:

• (Rail: active, Hexapod: idle)

• (Rail: brake, Hexapod: idle)

• (Rail: washout, Hexapod: active)

• (Rail: washout, Hexapod: brake)

• (Rail: washout, Hexapod: washout)

• (Rail: active, Hexapod: washout)

6 MASTER-SLAVE ALGORITHM

In this algorithm the roles played by the two transla-

tions are asymmetric. One dof is the master i.e. re-

sponsible for restituting the motion. The other dof is

the slave which has to counterbalance the ”bad” mas-

ter behaviors. It consists in producing opposite accel-

erations to the master’s when the latter brakes or goes

back to the neutral position (washout).

Working Modes

The working modes are different for each translation.

The master’s modes are:

1. active: the master dof tracks the treated reference

acceleration

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

212

Rail: active

Hexapod: idle

Rail: brake

Hexapod: idle

Rail: idle

Hexapod: active

Rail: washout

Hexapod: washout

Rail: washout

Hexapod: brake

Rail: washout

Hexapod: active

Rail: idle

Hexapod: brake

Rail: active

Hexapod: washout

Rail: brake

Hexapod: washout

decl_raildecl_rail

lim_raillim_rail

rail=0rail=0

decl_hexadecl_hexa

lim_hexalim_hexa

lim_raillim_rail

decl_raildecl_rail

decl_hexadecl_hexa

hexa=0hexa=0

ail=0

hexa=0hexa=0

Dealing with the limits

Figure 4: The symmetric automaton.

0 2 4 6 8 10 12 14 16 18 20

0.4

0.2

0.4

Hexapod

time(s)

Acceleration (m/s

)

0 2 4 6 8 10 12 14 16 18 20

Rail

time(s)

Acceleration (m/s

)

Figure 5: Simulation of the symmetric algorithm.

HYBRID MOTION CUEING ALGORITHMS FOR REDUNDANT ADVANCED DRIVING SIMULATORS

213

2. brake: parabolic braking

3. quick-washout: known starting point

4. washout: unknown starting point and unde-

tectable

5. idle: null acceleration

The slave’s modes are:

1. counter-brake: the slave dof tracks the accelera-

tion opposite to the master’s parabolic braking one

2. counter-washout: the slave dof tracks the acceler-

ation opposite to the master’s quick washout one

3. brake: parabolic braking

4. washout: unknown starting point and unde-

tectable

5. idle: null acceleration

Rules of Correct Operation

1. braking of both translation (master and slave)

must lead to the limit position with a null speed

2. braking must be followed by a washout motion.

The master’s washout is quick only if the slave is

within its free zone

3. the master could be (re)activated only starting

from its neutral position (the slave mustn’t be in

the braking mode)

4. after the counter-washout mode, the slave starts a

washout motion to its neutral position

6.1 The Master-slave Automaton

Figure 6 shows the master-slave automaton. The tran-

sitions have the same signiﬁcation as for the symmet-

ric automaton. Similarly, if we consider that braking

is instantaneous then this automaton could be reduced

to these subsequent states:

• Initial state: (Master: active, Slave: idle)

• (Master: brake, Slave: counter-brake): when

nearing the limits, the master brakes. The slave

provides the opposite acceleration so that the total

acceleration (perceived by the driver) is null.

• (Master: quick-washout, Slave: counter-

washout): after the master’s braking, a quick mo-

tion brings it to its neutral position. The slave

counterbalances this motion so that the overall ac-

celeration is null again.

• (Master: active, Slave: washout): the master

is reactivated once reaching its neutral position.

The slave starts the washout in order to improve

its future capacity of compensation. From this

state two permutations could occur: going back

to the initial state if the slave washout has ﬁnished

or switching to (Master: brake, Slave: counter-

brake) if the master reaches once again its limits.

The dashed box integrates all the states that describe

the automaton behavior when the slave couldn’t per-

form its counterbalancing role. It happens when the

slave reaches its limits and has to break. In this case,

the hybrid automaton starts a backward motion of

both dof that ends by going back to the initial state.

6.2 Simulations

The reference acceleration proﬁle is the same as be-

fore (scaled at 50% for a better visualisation). Rails

were chosen to be the slave whereas the hexapod

translation is chosen to be the master. In fact, as the

rails motion capacity is higher than the hexapod one,

the former is better suited to play the compensation

(slave) role.

The algorithm parameters are: braking (and

counter-braking) acceleration 0.3ms

−2

, quick

washout (and counter-washout) acceleration

0.5ms

−2

and slave braking acceleration 0.6ms

−2

As for the slave washout, µ and k were chosen to be

−1

and τ

−2

where τ = 1.45s. Figure 7 shows the

simulation results. We can distinguish 5 phases:

• (Hexapod: active, Rail: idle)

• (Hexapod: brake, Rail: counter-brake)

• (Hexapod: quick washout, Rail: counter-

washout)

• (Hexapod: active, Rail: washout)

• (Hexapod: active, Rail: idle)

7 CONCLUSION

In this paper we have presented two motion cueing

algorithms based on the hybrid systems framework.

These two algorithms exploit the redundancy of the

simulators to maintain the reproduction of motion

sensations despite the robot displacement limitations.

The symmetric algorithm presents a reliable ini-

tial restitution. However it generates incoherent sen-

sations due to signiﬁcant braking magnitudes. The

Master/Slave algorithm has a lesser restitution capac-

ity but it reduces considerably bad sensations by pro-

viding a full compensation (null sensations at the level

of the driver) of braking and washout motions.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

214

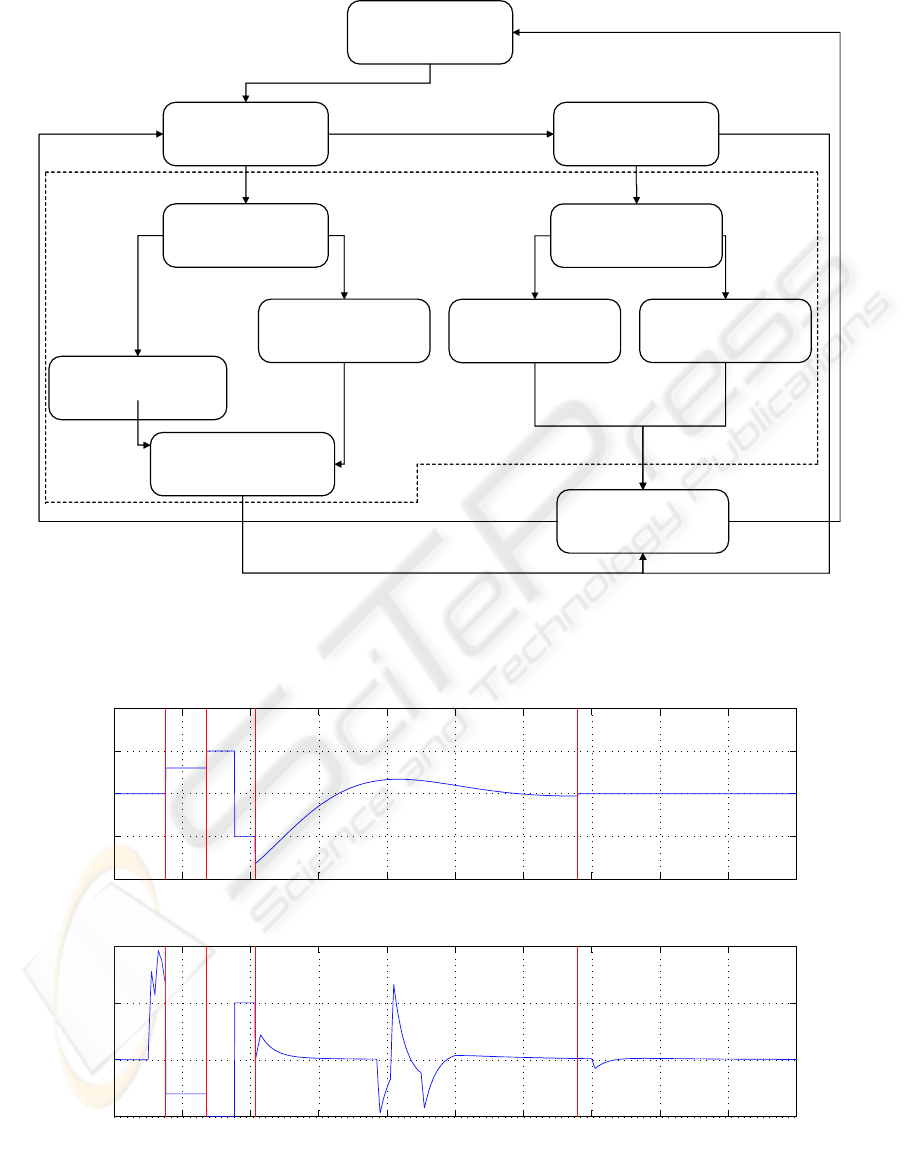
Master: active

Slave: idle

Master: brake

Slave: counter-brake

Master: quick-wash.

Slave: counter-wash.

Master: brake

Slave: brake

Master: washout

Slave: brake

Master: brake

Slave: washout

Master: washout

Slave: washout

Master: washout

Slave: brake

Master: idle

Slave: brake

Master: washout

Slave: washout

Master: active

Slave: washout

slave=0

decl_master

lim_master master=0decl,master

decl_slave

lim_slave

lim_master

lim_slave

lim_master

master=0

lim_slave

master=0

lim,slave

master=0

decl_slave

Dealing with the limits

Figure 6: The master-slave automaton.

0 2 4 6 8 10 12 14 16 18 20

0.5

Hexapod : Master

time(s)

Acceleration (m/s

)

0 2 4 6 8 10 12 14 16 18 20

0.5

Rail : Slave

time(s)

Acceleration (m/s

)

Figure 7: The master-slave simulations.

HYBRID MOTION CUEING ALGORITHMS FOR REDUNDANT ADVANCED DRIVING SIMULATORS

215

REFERENCES

Angelaki, D. and Dickman, J. (2004). Gravity or transla-

tion: Central processing of vestibular signals to detect

motion. Journal of Vestibular Research.

Dagdelen, M. (2005). Restitution des stimuli inertiels en

simulation de conduite. PhD thesis, Ecole des Mines

de Paris - Renault.

Elloumi, H. (2006). Commande des plate-formes avances

de simulation de conduite. PhD thesis, Ecole des

Mines de Paris, Centre de Math

ematiques Appliqu

ees.

Merlet, J. (2000). Parallel Robots. Kluwer Academic Pub-

lishers.

Parrish, R., Dieudonne, J., and Martin Jr., D. (1975). Coor-

dinated adaptive washout for motion simulators. Jour-

nal of Aircraft.

Reymond, G., Heidet, A., Canry, M., and Kemeny, A.

(2002). Validation of Renault’s dynamic simulator for

adaptive cruise control experiments. Driving Simula-

tion Conference.

Telban, R., Cardullo, F., and Guo, L. (2000). Investigation

of mathematical models of otolith organs for human

centered motion cueing algorithms. In AIAA Modeling

and Simulation Technologies Conference, Denver CO.

Van der Shaft, A. and Schumacher, H. (1999). An intro-

duction to hybrid dynamical systems. Springer-Verlag,

Lecture Notes in Control, 251.

Zaytoon, J. (2001). Syst

emes dynamiques hybrides. Hermes

Sciences Publications.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

216