KINEMATICS AND DYNAMICS ANALYSIS FOR A HOLONOMIC
WHEELED MOBILE ROBOT
Ahmed El-Shenawy, Achim Wagner and Essam Badreddin
Computer Engineering, University of Mannheim , B6. 23-27 part B, Mannheim, Germany
Keywords:
Modeling, Robot Kinematics, Robot Dynamics, Analysis.
Abstract:
This paper presents the kinematics and the dynamics analysis of the holonomic mobile robot C3P. The robot
has three caster wheels with modular wheel angular velocities actuation. The forward dynamics model which
is used during the simulation process is discussed along with the robot inverse dynamics solution. The in-
verse dynamics solution is used to overcome the singularity problem, which is observed from the kinematic
modeling. Since both models are different in principle they are analyzed using simulation examples to show
the effect of the actuated and non actuated wheel velocities on the robot response. An experiment is used to
illustrate the performance of the inverse dynamic solution practically.
1 INTRODUCTION
Wheeled mobile robots became an important tool in
our daily life. They are found in a multitude of ap-
plication such as guiding disabled people in muse-
ums (Burgard et al., 2002; Steinbauer and Wotawa,
2004) and hospitals (Kartoun et al., 2006), transport-
ing goods in warehouses, manipulation of army ex-
plosives (Bruemmer et al., 1998), or securing impor-
tant facilities (Chakravarty et al., 2004).
Wheeled mobile robots are categorized into two
main types: holonomic and non-holonomic, which
are the mobility constraints of the mobile robot plat-
form (Yun and Sarkar, 1998). A holonomic config-
uration implies that the number of robot velocities
DOF (Degrees Of Freedom) is equal to the number
of position coordinates. The main advantage of holo-
nomic mobility is the ability of efficient maneuver-
ing in narrow places. In the last two decades, many
considerable research efforts addressing the mobility
of holonomic wheeled mobile robots were done (Ful-
mer, 2003; Moore and Flann, 2000) and (Yamashita
et al., 2001).
Usually, kinematic modeling is used in the field
of WMRs (Wheeled Mobile Robot) to obtain stable
motion control laws for trajectory following or goal
reaching (Khatib et al., 1997; Ram
´
ırez and Zeghloul,
2000). Using the dynamics modeling during the sim-
ulation process results in a better control design. By
comparing its results to the practical implementation,
a better precision and more variables assumption are
achieved in comparison to the kinematics model.
The dynamic modeling is much more complex
than the kinematic modeling. Furthermore, the kine-
matic modeling is required for deriving the dynamic
model. Hence, it is assumed that the velocity and ac-
celeration solutions can be solved without any diffi-
culty. Generally, the main property of the dynamic
model is that it involves the forces that act on the
multibody system and its inertial parameters such as
: mass, inertia, with respect to the center of gravity
(Albagul and Wahyudi, 2004; Asensio and Montano,
2002).
The holonomic mobile robot ”C3P” (Caster 3
wheeled Platform) is described geometrically in sec-
tion 2. The singularity problem found in the C3P con-
figuration is illustrated in section 3 through the kine-
matic analysis. The forward dynamic model and the
inverse dynamic solution are presented and analyzed
in section 4 to show their different structure. Few sim-
ulation examples are shown to illustrate the effect of
the actuated and non-actuated variables on the robot
behavior using the inverse dynamic solution. In sec-
tion 5, a lab experiment is presented to show the per-
485
El-Shenawy A., Wagner A. and Badreddin E. (2007).
KINEMATICS AND DYNAMICS ANALYSIS FOR A HOLONOMIC WHEELED MOBILE ROBOT.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 485-491
DOI: 10.5220/0001650404850491
Copyright
c
 SciTePress

formance of the solution on the practical implemented
module.
2 THE PLATFORM
CONFIGURATION
The C3P WMR is a holonomic mobile robot, which is
previously discussed in (Peng and Badreddin, 2000).
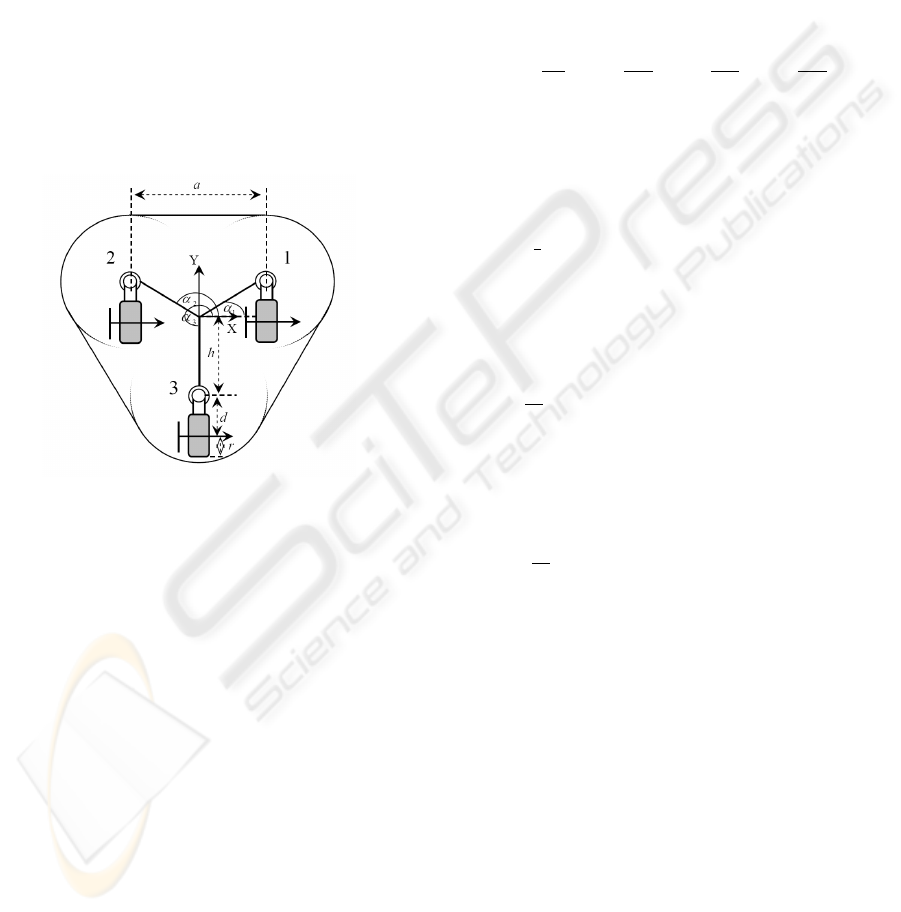
The C3P has three caster wheels attached to a trian-
gular shaped platform with smooth rounded edges as
shown in Fig. (1). Each caster wheel is attached to
each hip of the platform. The platform origin co-
ordinates are located at its geometric center, and the
wheels are located with distance h from the origin and
α
1
= 30
o
, α
2
= 150
o
, and α
3
= 270
o
shifting angles,
Figure 1: C3P platform configuration.
where
X,Y,φ : WMR translation and rotation displace-
ment.
θ
s
i
: the steering angle for wheel i.
r,d : the wheel radius and the caster wheel offset.
The conventional Caster wheel has three DOF due
to the wheel angular velocity
˙
θ
x
i
, the contact point an-
gular velocity
˙
θ
c
i
and the steering angular velocity
˙
θ
s
i
.
The unique thing about the C3P is that it has wheels
angular velocities actuation only (
˙
θ
x
i
) with no steer-
ing angular actuation, which makes the model modu-
lar and more challenging.
3 KINEMATICS MODELING AND
ANALYSIS
For WMRs’ mobility analysis and control, the kine-
matics modeling is needed. Furthermore, calculat-
ing the velocity and acceleration variables are impor-
tant in the dynamics modeling procedures. In order
to analyze and derive the C3P mathematical models,
some variables are assigned, such as the following:
the robot position vector p = [X Y φ ]
T
, the wheel an-
gles vector q
x
= [θ
x
1
θ
x
2
θ
x
3
]
T
, the steering angles
vector q
s
= [θ
s
1
θ
s
2
θ
s
3
]
T
, and the contact angles vec-
tor q
c
= [θ
c
1
θ
c
2
θ
c
3
]
T
. By differentiating the robot
and wheel vectors with respect to time, the robot and
wheel velocities are
˙p =
dp
dt
, ˙q
x
=
dq
x
dt
, ˙q
s
=
dq
s
dt
, ˙q
c
=
dq
c
dt
. (1)
From the generalized inverse kinematic solution
described in (Muir, 1987), the wheel angular velocity
inverse kinematic solution is
˙q
x
= J
in
x
˙p
J
in
x
=
1
r


−S(θ
s
1
) C(θ
s
1
) h C(α
1
− θ
s
1
)
−S(θ
s
2
) C(θ
s
2
) h C(α
2
− θ
s
2
)
−S(θ
s
3
) C(θ
s
3
) h C(α
3
− θ
s
3
)


(2)
while the steering angular actuation is
˙q
s
= J
in
s
˙p
J
in
s
=
−1
d


C(θ
s
1
) S(θ
s
1
) −h S(α
1
− θ
s
1
) + d
C(θ
s
2
) S(θ
s
2
) −h S(α
2
− θ
s
2
) + d
C(θ
s
3
) S(θ
s
3
) −h S(α
3
− θ
s
3
) + d


(3)
and the contact angular velocity inverse solution is
˙q
c
= J
in
c
˙p
J
in
c
=
−1
d


−S(θ
s
1
) C(θ
s
1
) −h C(α
1
− θ
s
1
)
−S(θ
s
2
) C(θ
s
2
) −h C(α
2
− θ
s
2
)
−S(θ
s
3
) C(θ
s
3
) −h C(α
3
− θ
s
3
)


(4)
where ”C” stands for ”cos” and ”S” stands for ”sin”.
The solution (2) shows singularities for some steer-
ing angles configurations. The singularity appears
only when the steering angles are equal. For example,
when the steering angles are −90
o
, the robot velocity
˙
Y is not actuated (Fig. (2-a)), and when they are 0
o
the
velocity
˙
X is not actuated (Fig. (2-c)). The steering
configuration in Fig. (2-b) gives singular determent
for the matrix J
in
x
with −45
o
steering angles although
all the robot DOFs are actuated.
Obviously, the direction of [−1 1 0]
T
is not ac-
tuated, which concludes the following; if all steering
angles yield the same value, then the robot is not ac-
tuated in the direction parallel to the wheel axes. Fig.
(2-d) represents a non-singular steering wheels con-
figuration condition.
Solutions (3) and (4) can be used to overcome the
singularity practically by adding practical actuation
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
486

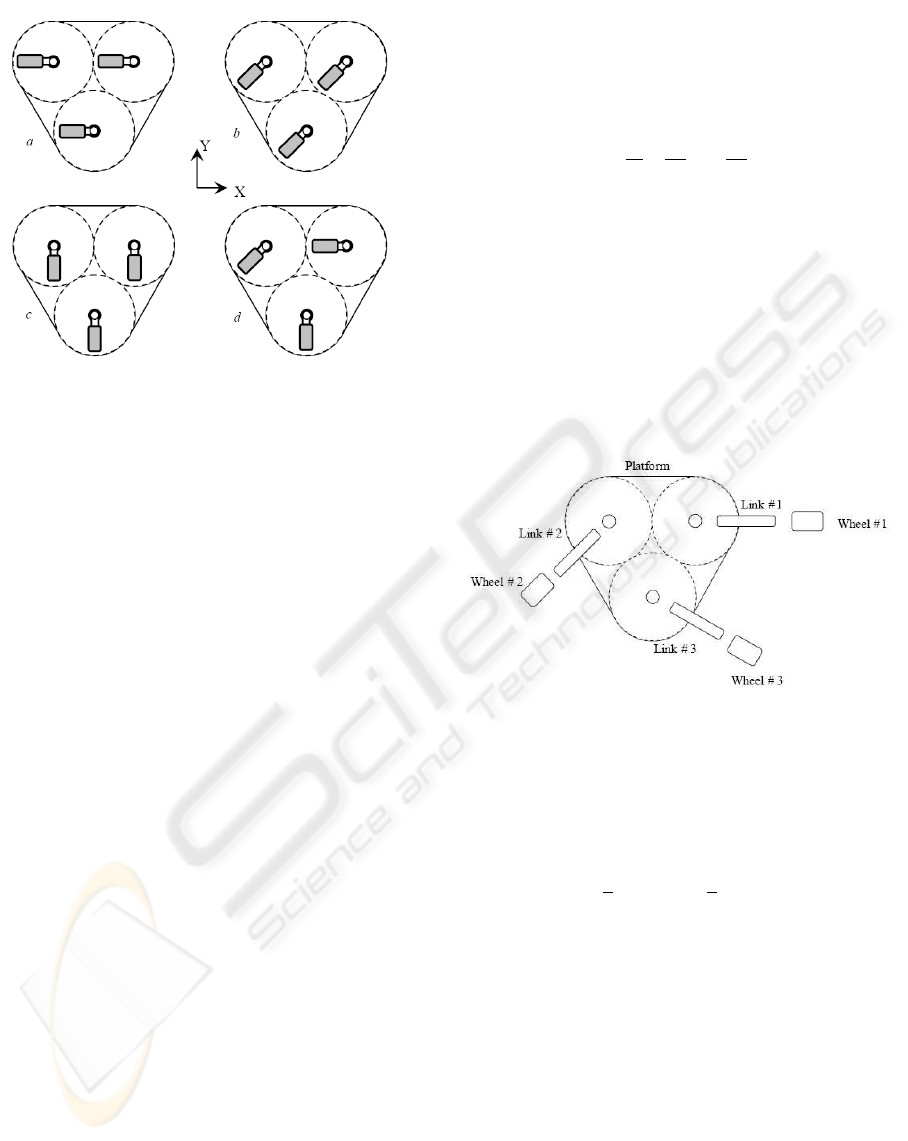
Figure 2: Different steering angles configurations.
to the steering angular velocities, or theoretically by
virtually actuating the steering angular velocities (El-
Shenawy et al., 2006c).
The forward sensed kinematics used in (El-
Shenawy et al., 2006a) shows that the sensed vari-
ables are sufficient for robust sensing and slippage de-
tection through the following equation
˙p = J
f
x
˙q
x
+ J
f
s
˙q
s
, (5)
where J
f
x
and J
f
s
are the sensed forward solutions for
the wheel angular and steering angular velocities re-
spectively. The derivative of equation (5), yields the
robot accelerations,
¨p = J
f
x
¨q
x
+ J
f
s
¨q
s
+ g(q
s
, ˙q
x
, ˙q
s
), (6)
from equations (2), (3) and the inversion method pro-
posed in (Muir, 1987) the inverse actuated kinematic
accelerations is

¨q
x
¨q
s

=

J
in
x
J
in
s

¨p− g
cs
(q
s
, ˙p) (7)
4 DYNAMIC MODELING AND
ANALYSIS
4.1 Euler Lagrange
The dynamic equations of motion are derived using
the Euler-Lagrangian method (Naudet and Lefeber,
2005) based on the Lagrangian function
L = K − P, (8)
where K denotes the kinetic energy and P denotes the
potential energy. Since the C3P is assumed to drive
on a planar surface, P is zero.
The Lagrangian dynamic formulation is described
as
τ =
d
dt

∂L
∂ ˙q

−
∂L
∂q
, (9)
where τ is the vector of actuated torques.
The C3P is considered as a closed chain multi-
body system. To derive the dynamic model of the
C3P, the system is converted into an open chain struc-
ture. First, the dynamic model of each serial chain is
evaluated using the Lagrangian dynamic formulation
(9). Second, the platform constraints incorporate the
open chain dynamics into a closed chain dynamics.
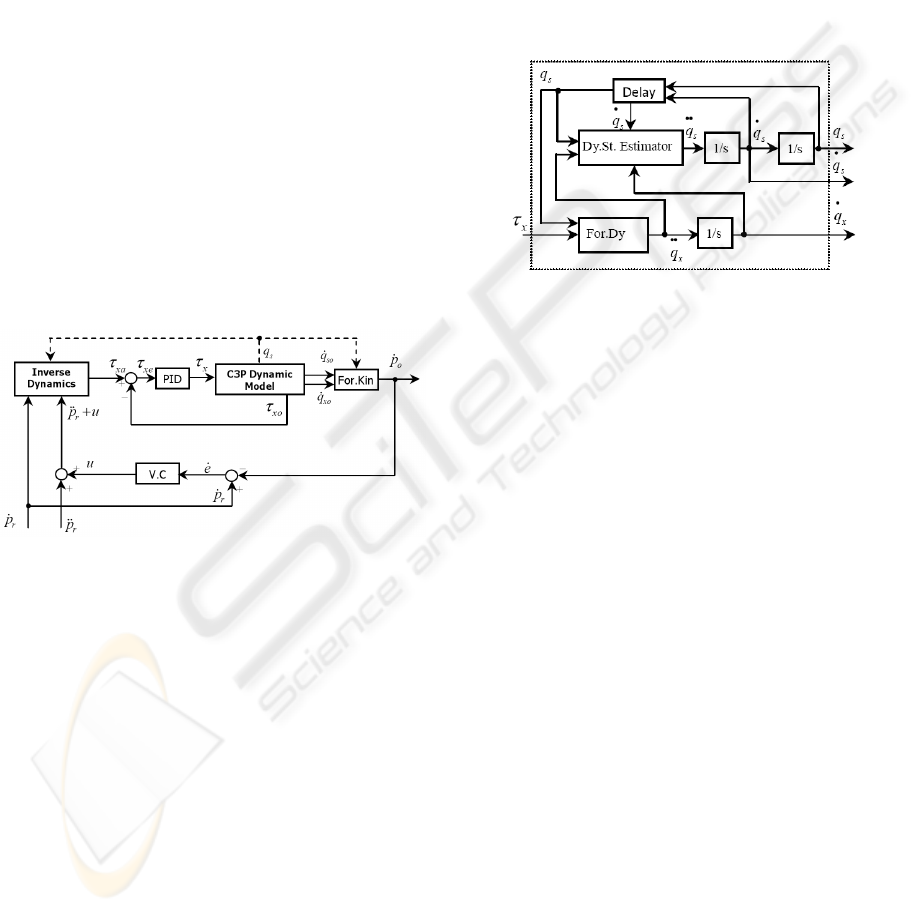
The robot consists of 7 parts; 3 identical wheels, 3
identical links and one platform (Fig.(3)).
Figure 3: The C3P parts structure.
The kinetic energy of the rigid body depends on
its mass, inertia , linear and angular velocities as de-
scribed by the following equation
K =
1
2
m V
T
V +
1
2
Ω
T
I Ω (10)
where,
m, I : mass and inertia of the rigid body.
V, Ω : linear and angular velocity at the center of
gravity of the rigid body.
The sum of the platform kinetic energies equa-
tions results in the following Lagrangian function
L =
3
∑
i=1
K
wi
+
3
∑
i=1
K
li
+ K
pl
, (11)
where K
wi
, K
li
are the wheel and link i kinetic energies
respectively, while K
pl
is the platform kinetic energy.
The wheel co-ordinates q can be considered as the ac-
tuated displacements and ˙q as the actuated velocities,
KINEMATICS AND DYNAMICS ANALYSIS FOR A HOLONOMIC WHEELED MOBILE ROBOT
487

while τ is the external torque/force vector. The overall
dynamics of the robot can be formulated as a system
of ordinary differential equations whose solutions are
required to satisfy the WMR constraints through the
following force/torques vector equation
τ = M(q) ¨q+ G(q, ˙q) (12)
where, M(q) is the inertia matrix, G(q, ˙q) contains the
centripetal and Coriolis terms.
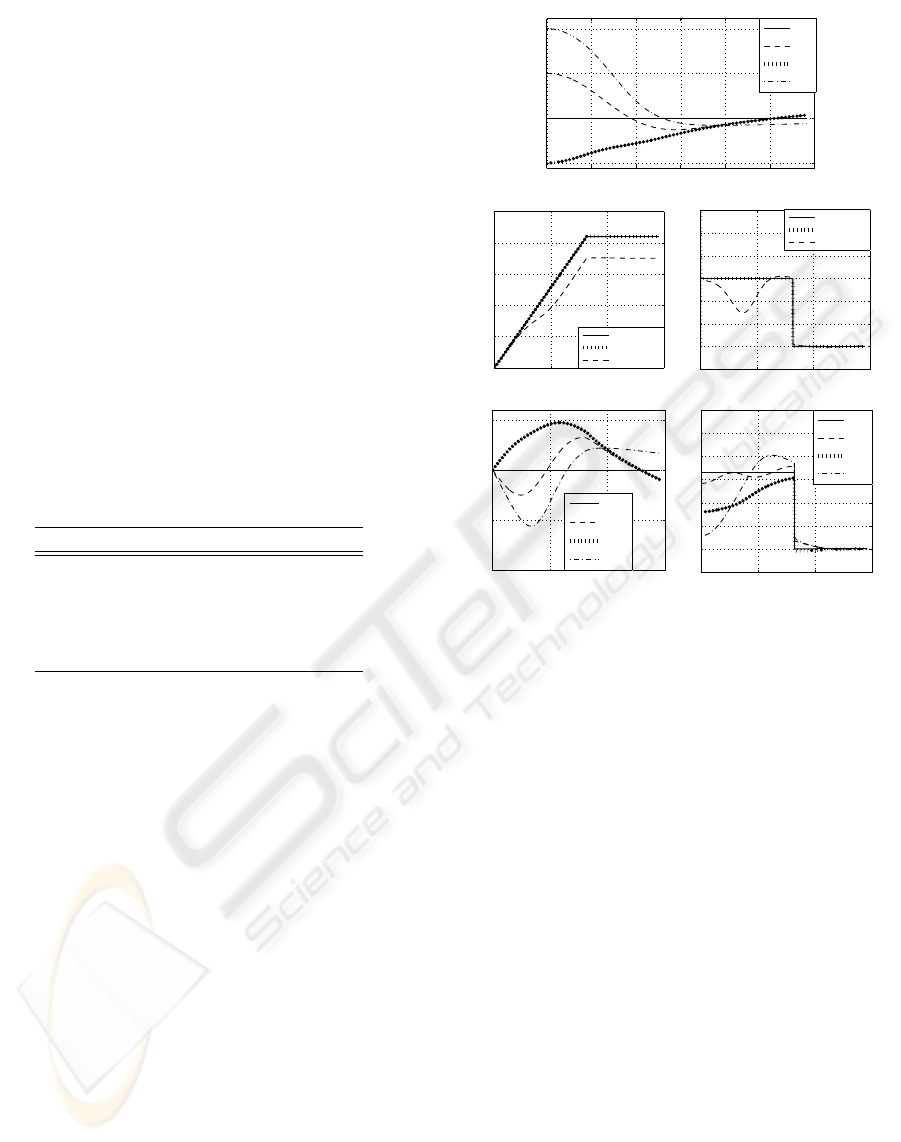
4.2 Control Structure Design
The C3P control structure contains three main mod-
els (Fig.(4)): the forward kinematics for calculating
the C3P velocities, the C3P forward dynamic model
which models the C3P practical prototype on the sim-
ulation level, and the inverse dynamics solution.
The velocity controller (V.C) calculates a control
signal u from the velocity error ˙e = ˙p
r
− ˙p
o
, which
is added to the reference acceleration signal ¨p
r
. The
reference robot velocities ˙p
r
and accelerations ¨p
r
are
used in the inverse dynamic solution to deliver the ac-
tuated wheels torques τ
xa
.
Figure 4: Robot closed-loop structure.
The forward dynamics consists of two main equa-
tions; the Wheels Torques Dynamics (WTD) and the
Dynamic Steering Estimator (DSE), which were pro-
posed in (El-Shenawy et al., 2006b). The wheel angu-
lar velocities are calculated using the wheels torques
dynamic equation of motion
τ
x
= M(q
s
) ¨q
x
+ G
x
(q
s
, ˙q
x
), (13)
with respect to the actuated wheels torques, where
τ
x
= [τ
x
1
τ
x
2
τ
x
3
]
T
. The steering angles and the steer-
ing angular wheel velocities are recursively calculated
by the steering dynamic estimator
¨q
s
= M
−1
ss
M
xx
¨q
x
+ M
−1
ss
G
ssx
(q
s
, ˙q
s
, ˙q
x
) (14)
corresponding to the angular wheels velocities and ac-
celerations generated due to the applied wheel torque
resulting from equation (13).
The C3P dynamic model shown in Fig. (5) has
the actuated wheel torques τ
x
as an input, while the
outputs are the sensed wheel velocities ˙q
x
, the steer-
ing angular velocities ˙q
s
, and the steering angles q
s
.
Since the steering angular velocities are actuated by
the angular wheel velocities, the angular wheel ve-
locities ˙q
x
and accelerations ¨q
x
are the main inputs
of the steering dynamic estimator. The steering an-
gles q
s
and steering angular velocities ˙q
s
are delayed
by unity time interval because the steering dynamic
model is calculated recursively according to (14).
Figure 5: The C3P Dynamic Model.
The inverse dynamic solution proposed is imple-
mented in the velocity control loop to overcome the
singularity with simpler velocity controller and better
performance. The inverse dynamic equation depends
on the platform constraints, which are described in the
forward kinematic solution. They are combined using
Lagrangian formulation and the dynamic torque equa-
tion (9) to obtain the described wheel torques equa-
tion
τ
x
a
=

M
x
a
M
s
a


¨q
x
¨q
s

+ G
sx
a
( ˙q
x
, ˙q
s
,q
s
) (15)
The matrix M
x
a
is the inverse dynamic solution for
actuating the wheels torques τ
x
a
, while the matrix M
s
a
is the inverse dynamic solution for actuating the steer-
ing angular acceleration ¨q
s
using the wheel torques
τ
x
a
. The inverse dynamics solution is a relation be-
tween the desired robot velocities and accelerations
(˙q, ¨q) as an input and the actuated applied torques
of the wheels (τ
x
a
) as an output. However, the dy-
namic torque equation (15) is a function of ¨q
x
, ¨q
s
, ˙q
x
,
and ˙q
s
. By using the velocity and acceleration inverse
kinematic solutions(2, 3, 4 and 7), the desired torque
equation is achieved and the actuation characteristics
of the steering angular velocities and accelerations are
included in the inverse dynamic solution as well. As
a result the actuated torques equation will have the
robot velocities ˙p and accelerations ¨p as input vari-
ables
τ
x
a
= M
x
(q
s
) ¨p+ G
xi
(q
s
, ˙p) (16)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
488

M
x
=

M
x
a
M
s
a


J
in
x
J
in
s

, (17)
G
xi
= G
sx
a
(q
s
, ˙p) −

M
x
a
M
s
a

g
cs
(q
s
, ˙p) (18)
4.3 Model Analysis
The proposed inverse and forward dynamic solutions
are different in structure and mathematical represen-
tation as well. However, both models should yield
the inversion of each other. Therefore some simula-
tion examples are done and analyzed in this section to
illustrate the performance of the model. The simula-
tions are done using the structure shown in Fig. (4)
with zero values for the velocity (V.C.) and the axes
level control parameters to disable their effects. The
C3P parameters are set to be exactly like the practical
prototype, which are described in Table 1.
Table 1: The C3P parameters.
C3P Parameters Value Units
h 0.343 m
d 0.04 m
r 0.04 m
M
p
(Platform mass) 25 Kg
I
p
(Platform inertia) 3.51 Kg m
2
Fig.(6) shows a comparison between two different
examples. The first example is a non singular condi-
tion, where the steering angles are θ
s
1
= θ
s
2
= θ
s
3
=
0
o
as shown in Fig. (2c). The input signal is a ramp
input in Y direction while the X translational and Φ
velocities are zeros. The input V
y
or
˙
Y is a ramp sig-
nal till 3.2 seconds then it is constant. The second
example is a non singular condition but with differ-
ent steering angles, where θ
s
1
= 45
o
,θ
s
2
= −45
o
and
θ
s
3
= 90
o
with the same ramp input signal. Fig. (6-
a) shows the trajectory of the steering angles, which
are indicated as (θ
s−oi
) for example one and (θ
s−i
) for
example two.
The reference input velocities maintain zero steer-
ing angles value. For the first example, the steering
angles keep their initial value, while in the second ex-
ample the steering angles were adjusted from their
initial value to the zero value. The steering wheel
adjustment took place due to the the step accelera-
tion input in Y direction. The robot output velocity
and acceleration Out − 1 result from the first example
(Fig. (6-b) &(6-c)), which follow the input signal as
well as the steering and wheel angular accelerations
(α
s−oi
,α
x−oi
) as shown in Fig. (6-d) &(6-e).
0 1 2 3 4 5 6
−45
0
45
90
Time (s)
θ
s
(
o
)
a) The steering angles
θ
s−oi
θ
s−1
θ
s−2
θ
s−3
0 2 4 6
0
0.02
0.04
0.06
0.08
0.1
Time (s)
V
y
(m/s)
b) Velocity in Y direction
Reference
Out−1
Out−2
0 2 4 6
−2
0
2
4
6
8
10
12
x 10
−3
Time (s)
a
y
(m/s
2
)
c) Acceleration in Y direction
Reference
Out−1
Out−2
0 2 4 6
−0.1
−0.05
0
0.05
Time (s)
α
s
(r/min
2
)
d) The steering angular acceleration
α
s−oi
α
s−1
α
s−2
α
s−3
0 2 4 6
−0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
Time (s)
α
x
(r/min
2
)
e) The wheel angular acceleration
α
x−oi
α
x−1
α
x−2
α
x−3
Figure 6: Simulation comparison for ramp input.
For the second example, the input acceleration and
the initial steering angles produce disturbances and
oscillations in the wheel angular acceleration ((α
x
i
=
0 for i ∈ {1,2,3} (Fig. (6-e)))). Such disturbances
produce oscillations in the steering angular accelera-
tions ((α
s
i
= 0 for i ∈ {1,2,3} (Fig. (6-d)))), which
results negative overshoot in the robot Y acceleration
(Out − 2) (Fig. (6-c))). In addition to the presence of
the dynamic delay in the forward dynamics solution
(Fig. (5)) and some simulation numerical errors the
overshoot appears.
When the robot velocity takes constant value the
desired wheel acceleration suddenly change from
value 0.17 (r/min
2
) to 0 (r/min
2
). Such input does
not cause multiple oscillations or high overshoots in
output signal (Fig. (6-d)).
The next simulation shows the responses of the
robot velocities and accelerations after enabling the
axes and robot level controllers. The robot starts from
the same initial steering angles but the input velocity
is ramp signal in X direction and Zero value in the Y
and the rotational velocities (Fig.(7-d)). Such input
yields the steering angles to reach −90
o
(Fig.(7-a)),
which is adjusted due to the wheel angular accelera-
KINEMATICS AND DYNAMICS ANALYSIS FOR A HOLONOMIC WHEELED MOBILE ROBOT
489

tions oscillations resulted in Fig. (7-b).
0 5 10 15
−90
−45
0
Time (s)
θ
s
(
o
)
a) The steering angles
θ
s
1
θ
s
2
θ
s
3
0 5 10 15
−0.2
−0.1
0
0.1
0.2
0.3
Time (s)
α
x
( r/min
2
)
b) The wheels angular accel.
α
x
1
α
x
2
α
x
3
0 5 10 15
−2
0
2
4
6
8
10
x 10
−3
Time (s)
a
x
(m/s
2
)
c) Accel. in X direction
Reference
Measured
0 5 10 15
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
Time (s)
V
x
(m/s)
d) Velocity in X direction
Reference
Measured
Figure 7: simulation responses for ramp input with singu-
larity configuration.
In the first seven seconds during the steering an-
gles adjustment, the output acceleration of the robot
X direction oscillates but it reach the desired value
as the steering angles settle with their desired values
(Fig.(7-c)). These oscillations affect the robot veloc-
ity output as well by oscillating around the desired
signal (Fig.(7-d)). In case of having Y as adesired di-
rection, the output signal will be exactly the same like
the input, because the effect of the delay unit in the
forward dynamics solution is negligible.
5 LAB EXPERIMENT
After analyzing the inverse and forward dynamic so-
lutions, the inverse dynamic solution is implemented
on the C3P prototype (Fig. (8)) to test its perfor-
mance practically. Therefore, an experiment was im-
plemented in the lab with the following initial steering
angles θ
s
1
= θ
s
2
= θ
s
3
= 135
o
and input robot veloc-
ities ˙p
r
= [0.5(m/s) 0.5(m/s) 0(r/min)]
T
. Such in-
put velocities yields the steering angles to flip 180
o
to
reach −45
o
or 315
o
values (Fig.(9-a)).
The steering angles θ
s
2
and θ
s
3
flipped after 2 sec-
onds in different directions (Fig.9c), causing oscilla-
tions in the robot velocities (Fig.(9-d), (9-e) & (9-f)).
After the fourth second, the first steering angle θ
s
1
flipped producing another overshoots in the robot ve-
locities. The robot velocities (Fig.(9-d), (9-e) & (9-f))
Figure 8: The C3P practical prototype.
0 2 4 6 8
−45
45
135
225
315
Time (s)
θ (
o
)
a) The steering angles
θ
s
1
θ
s
2
θ
s
3
0 2 4 6 8
−100
−50
0
50
100
150
Time (s)
ω
x
(r/min)
b) The wheels angular velocities
ω
x
1
ω
x
2
ω
x
3
0 2 4 6 8
−200
−100
0
100
200
Time (s)
ω
s
(r/min)
c) The steering angular velocities
ω
s
1
ω
s
2
ω
s
3
0 2 4 6 8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Time (s)
V
x
(m/s)
d) Linear C3P velocity in X direction
Reference
Measured
0 2 4 6 8
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Time (s)
V
y
(m/s)
e) Linear C3P velocity in Y direction
Reference
Measured
0 2 4 6 8
−3
−2
−1
0
1
2
Time (s)
Φ
dot
(r/min)
f) Angular C3P velocity around Z axis
Reference
Measured
Figure 9: Practical Lab results for the C3P prototype.
are measured with respect to the floor frame of co-
ordinates, which illustrates how the responses follow
the reference value in the steady state.
The main advantage and main problem of the C3P
configuration are the same. This is the non direct ac-
tuation of the steering angular velocities of the wheel.
Such a problem is very challenging from the theoret-
ical and practical point of view. Since the steering
angular velocities are virtually actuated, their behav-
ior can not be exactly predicted. However, the for-
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
490

ward dynamic model is the main factor in deriving
the inverse dynamic solution and designing its con-
trol structure along with tuning its parameters. These
information are very useful during the practical im-
plementation takes place, as in the last experiment.
6 CONCLUSION
The kinematics and the dynamics models of the holo-
nomic mobile robot C3P are presented in this paper.
The singularity problem found in such actuation con-
figuration is described by the inverse kinematic so-
lution. The dynamic analysis showed the effect of
the wheel and steering angular accelerations of the
caster wheels on the inverse dynamic behavior with
and without velocity controllers. Although the inverse
and forward dynamic models are different in struc-
ture, they yield the inversion of each other. The steer-
ing angular acceleration plays a very important rule in
calculating the reference actuated signal to the plat-
form to overcome the robot singularities and to adjust
its steering angles. The simulation examples showed
the model dynamic analysis through the robot accel-
eration variables, and the practical experiment proved
the effectiveness of the control structure.
REFERENCES
Albagul, A. and Wahyudi (2004). Dynamic modelling and
adaptive traction control for mobile robots. Int. Jor. of
Advanced Robotic Systems, Vol.1,No.3.
Asensio, J. R. and Montano, L. (2002). A kinematic and
dynamic model-based motion controller for mobile
robots. 15th Triennial World Congress.
Bruemmer, J., Marble, J., and Dudenhoffer, D. (1998). In-
telligent robots for use in hazardous dor environments.
Burgard, W., Trahanias, P., Haehnel, D., Moors, M., Schulz,
D., Baltzakis, H., and Argyros, A. (2002). Tourbot
and webfair: Web-operated mobile robots for tele-
presence in populated exhibitions. IEEE/RSJ Conf.
IROS’02, Full day workshop in ”Robots in Exhibi-
tions.
Chakravarty, P., Rawlinson, D., and Jarvis, R. (2004).
Distributed visual servoing of a mobile robot for
surveillance applications. Australasian Conference on
Robotics and Automation (ACRA).
El-Shenawy, A., Wagner, A., and Badreddin, E. (2006a).
Controlling a holonomic mobile robot with kinematics
singularities. The 6th World Congress on Intelligent
Control and Automation.
El-Shenawy, A., Wagner, A., and Badreddin, E. (2006b).
Dynamic model of a holonomic mobile robot with
actuated caster wheels. The 9th International Con-
ference on Control, Automation, Robotics and Vision,
ICARCV.
El-Shenawy, A., Wagner, A., and Badreddin, E. (2006c).
Solving the singularity problem for a holonomic mo-
bile. 4th IFAC-Symposium on Mechatronic Systems
(MECHATRONICS 2006).
Fulmer, C. R. (2003). Design and fabrication of an omni-
directional vehicle platform. Master thesis University
of Florida.
Kartoun, U., Stern, H., Edan, Y., Feied, C., Handler, J.,
Smith, M., and Gillam, M. (2006). Vision-based au-
tonomous robot self-docking and recharging. 11th In-
ternational Symposium on Robotics and Applications
(ISORA).
Khatib, O., Jaouni, H., Chatila, R., and Laumond, J. P.
(1997). Dynamic path modification for car-like
nonholonomic mobile robots. IEEE Intl. Conf. on
Robotics and Automation.
Moore, K. and Flann, N. (2000). Six-wheeled omnidirec-
tional autonomous mobile robot. IEEE Control Sys-
tems Magazine.
Muir, P. (1987). Modeling and control of wheeled mobile
robots. PhD dissertation Carnegie mellon university.
Naudet, J. and Lefeber, D. (2005). Recursive algorithm
based on canonical momenta for forward dynamics of
multibody systems. Proceedings of IDETC/CIE.
Peng, Y. and Badreddin, E. (2000). Analyses and simulation
of the kinematics of a wheeled mobile robot platform
with three castor wheels.
Ram
´
ırez, G. and Zeghloul, S. (2000). A new local path
planner for nonholonmic mobile robot navigation in
cluttered environments. IEEE Int. Conf. on Robotics
and Automation.
Steinbauer, G. and Wotawa, F. (2004). Mobile robots in ex-
hibitions, games and education. do they really help?
CLAWAR/EURON Workshop on Robots in Entertain-
ment, Leisure and Hobby.
Yamashita, A., Asama, H., Kaetsu, H., Endo, I., and Arai,
T. (2001). Development of omni-directional and step-
climbing mobile robot. Proceedings of the 3rd In-
ternational Conference on Field and Service Robotics
(FSR2001).
Yun, X. and Sarkar, N. (1998). Unified formulation of
robotic systems with holonomic and nonholonomic
constrains. IEEE Trans. on robotics and automation,
Vol.12, pp.640-650.
KINEMATICS AND DYNAMICS ANALYSIS FOR A HOLONOMIC WHEELED MOBILE ROBOT
491