
OPTIMAL NONLINEAR IMAGE DENOISING METHODS IN
HEAVY-TAILED NOISE ENVIRONMENTS
Hee-il Hahn
Dept. Information and Communications Eng. Hankuk University of Foreign Studies, Yongin, Korea
Keywords: Nonlinear denoising, robust statistics, robust
estimation, maximum likelihood estimation, myriad filter,
Cauchy distribution, amplitude-limited sample average filter, amplitude-limited myriad filter.
Abstract: The statistics for the neighbor differences between the particular pixels and their neighbors are introduced.
They are incorporated into the filter to enhance images contaminated by additive Gaussian and impulsive
noise. The derived denoising method corresponds to the maximum likelihood estimator for the heavy-tailed
Gaussian distribution. The error norm corresponding to our estimator from the robust statistics is equivalent
to Huber’s minimax norm. This estimator is also optimal in the respect of maximizing the efficacy under the
above noise environment. It is mixed with the myriad filter to propose an amplitude-limited myriad filter. In
order to reduce visually grainy output due to impulsive noise, Impulse-like signal detection is introduced so
that it can be processed in different manner from the remaining pixels. Our approaches effectively remove
both Gaussian and impulsive noise, not blurring edges severely.
1 INTRODUCTION
Noise introduced into images via image acquisition
devices such as digital cameras can be adequately
assumed to be additive zero-mean Gaussian
distributed. Such impulsive noise as caused by
transmission of images can be more approximated as
α
stable distribution. In general, the noise with
zero-mean and independent properties can be easily
removed by locally averaging pixel values. A mean
filter is known to be a maximum likelihood
estimator for additive Gaussian noise and is optimal
in the sense of minimizing mean square error. This
filter, however, tends to degrade the sharpness of the
boundaries between regions of an image although it
effectively removes noise inside the smooth regions.
Basically linear filters can not overcome this
problem. That is why nonlinear methods should be
employed for this purpose. One of the simplest
nonlinear filtering algorithms is the median-based
filter. It is a maximum likelihood estimator for
Laplacian distribution. It has a relatively good
property of preserving fine details except for thin
lines and corners. It is known to be robust to
impulsive noise. Stack filter, weighted median and
relaxed median are among its variations to improve
the performance. Median-based methods basically
select one of the samples in the input window. Thus,
it is known that they can not reduce noise effectively.
Motivated by the above limitations, several kinds of
myriad filters have been proposed, which are known
to be maximum likelihood estimator under Cauchy
distribution (Gonzalez, Arce, 2001), (Zurbach, et al.,
1996). Optimality of myriad filters are presented
under
α
stable distributions (Gonzalez, Arce, 2001).
(Hamza and Krim, 2001)
proposed mean-relaxed
median and mean-LogCauchy filters by combining a
mean filter with a relaxed median or LogCauchy
filter. They are maximum likelihood estimators
under the assumption that the noise probability
distribution is a linear combination of normal
distribution and heavy-tailed distribution such as
Laplacian or Cauchy distribution. Another popular
methods are the anisotropic diffusion techniques into
which a variety of research has been devoted since
the work of (Perona and Malik, 1990). Recent
researches have shown that nonlinear methods such
as median filters and anisotropic diffusions can be
reinterpreted using the theory of robust statistics
(Huber, 1981). Robust-statistics-based denoising
algorithms are developed, which deal with intensity
discontinuities to adapt the analysis window size
(Rabie, 2005). He chose a Lorenzian redescending
estimator in which the influence function tends to
zero with increasing distance.
424
Hahn H. (2007).
OPTIMAL NONLINEAR IMAGE DENOISING METHODS IN HEAVY-TAILED NOISE ENVIRONMENTS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 424-429
DOI: 10.5220/0001650604240429
Copyright
c
SciTePress

A large number of image denoising algorithms
proposed so far are limited to the case of Gaussian
noise or impulsive noise, not to both of them. The
algorithms tuned for Gaussian noise or impulsive
noise alone present serious performance degradation
in case images are corrupted with both kinds of
noise. To tackle the problem, an amplitude-limited
sample average filter is proposed. It is also a
maximum likelihood estimator in the density
function which is Gaussian on
()
,
δ
δ
−
, but
Laplacian outside the region. Its idea is incorporated
into the myriad filter to propose an amplitude-
limited myriad filter. In order to reduce visually
grainy output due to impulsive noise, Impulse-like
signal detection is introduced so that it can be
processed in different manner from the remaining
pixels. Our approaches effectively remove both
Gaussian and impulsive noise, not blurring edges
severely.
After reviewing the problems of finding the best
estimate of a model in terms of maximum likelihood
estimate (MLE), given a set of data measurements,
our estimators are interpreted based on the theory of
robust estimation in both Gaussian and impulsive
noise environment.
2 NOISE STATISTICS
In deriving our robust denoising filter, we employ an
observed image model corrupted with additive
Gaussian and impulsive noise
(1)
2
i ∈ Z
where
i
is a zero-mean additive white Gaussian
noise plus impulsive noise.
i
n
is uncorrelated to the
image sequence
i
n
x
and
i
is the observed noise-
contaminated image sequence. In this case,
i
n
can
be assumed to have a density function whose tails
are heavier than Gaussian. To ensure the
unbiasedness of the maximum likelihood estimator,
its density function is assumed to be symmetric. The
density function of
i
is assumed to be Gaussian on
y
n
(
,
)
δ
δ
−
, but Laplacian outside the region It has a
shape of Gaussian distribution with heavier
exponential tails given by
(2)
where, of course,
C
should be chosen so that the
density
(
)
f
x
has unit area by proper adjustment of
and
a
δ
. Its statistics can be modelled as symmetric
α
stable
()SS
α
distribution.
3 OUR PROPOSED FILTERS
3.1 Amplitude-Limited Sample
Average Filter
Let us found out the MLE of the mean of a normal
random variable with known variance from
M
independent observations. The density function for
M
independent observations is
. (3)
()
()
()
()
2
2
1
1
2
2
2
2
1
/
2
M
i
i
x
M
M
px e
μ
σ
μ
πσ
=
−−
∑
=
The MLE of
μ
that maximizes the above density
function is given by
. . (4)
()
2
11
1
ˆ
arg min
MM
ii
ii
xx
M
μ
μ
μ
==
== −
∑∑
The MLE is just the sample mean and
ˆ
μ
is known to
be a minimum variance unbiased and consistent
estimate. This means that the MLE for estimating
the signal under the additive Gaussian model is a
mean filter. It can be interpreted as optimum filter in
the sense of mean-square errors.
Likewise, when the observations have a density of
Laplacian instead of Gaussian, the density function
for
M
independent observations is
(5)
and the MLE of
η
that maximizes the above
equation is given by
(6)
Its MLE corresponds to the median filter which
selects the sample located at the center after
arranging the observations in the ascending order.
Thus, combining the results given in Eq. (4) and (6)
we obtain the MLE of
θ
for the density function
given in Eq. (2).
()
()
()
2
2
2
/2
/2
/2
,
,
,
aax
ax
aax
Ce e x
fx Ce x
Ce e x
δδδ
δδδ
δ
δ
δ
δ
−−−
−
−+
>
=−≤≤
<−
⎧
⎪
⎪
⎨
⎪
⎪
⎩
()
()
1
2
2
1
/
2
M
i
i
x
L
M
M
px e
η
σ
η
σ
=
−−
∑
=
1
ˆ
arg min
M
i
i
x
η
η
η
=
=
−
∑
n=+,
iii
yx
OPTIMAL NONLINEAR IMAGE DENOISING METHODS IN HEAVY-TAILED NOISE ENVIRONMENTS
425

(7)
The corresponding filter can be easily implemented
by
(8)
where (9)
We call this filter as an amplitude-limited sample
average filter (ALSAF). The efficacy of the estimate
can be found out as follows,
(10)
In the above equation,
(
)
f
x
, given in Eq.(2),
represents the density function for each observation.
Since , Efficacy
ξ
has the
maximum value. Thus, the ALSAF given above is
the optimal estimate in terms of maximizing the
efficacy under the above noise environment. The
error norm corresponding to our estimator from the
robust statistics is given by
(11)
This is equivalent to Huber’s minimax norm (Huber,
1981), (Black, et al., 1998). To apply our denoising
filter, we need to choose the variables
a
and
δ
as
given in Eq. (2) and Eq. (9), which depends on the
statistics of the noisy images. The value of
δ
is
inversely proportional to the amount of outliers such
as impulsive noise. If the value of
δ
is equal to the
standard deviation
σ
of the density function given in
Eq. (2), the distribution will be similar to Gaussian,
which means that the outliers rarely exist. Thus,
δ
should be less than
σ
(typically
0.8
σ
δ
=
). The
probability
G
p
that the noise is greater than
δ
is
computed as
()
2
ˆ
arg min
ii
ii
xx
xx
θ
δδ
θ
θθ
≤>
=−+
⎧⎫
⎨⎬
⎩⎭
∑∑
(12)
()
2 2
22
2
2
aax a
G
k
C
pCe e dx e
And the probability
L
p
that the noise is less than
δ
is
(13)
where .
a
is chosen empirically for each specific image such
that
GL
p
p
=
to optimize the estimate. The ALSAF
is iteratively applied to reduce any residual noise by
estimating the variables
a
and
δ
from the statistics
of the neighbor differences at each iteration. The
algorithm stops when the residual error between the
current and the next estimate falls below some
threshold at each pixel, which is usually less than
δ
.
Recall the Perona-Malik (PM) anisotropic diffusion
(Perona and Malik, 1990)
(14)
where ,
∇
denotes divergency and gradient,
respectively. Since the robust estimation can be
posed as:
(15)
where
Ω
is the domain of the image. Eq. (15) can
be solved using the gradient descent as follows:
(16)
Comparing Eq. (14) with Eq. (16), we can obtain the
relation
(17)
Thus, our denoising algorithm can be implemented
using PM anisotropic diffusion by selecting the edge
stopping function
(
)
hx
given in Eq. (17) (Black, et
al., 1998).
−
()
1
ˆ
M
i
i
g
x
δ
θ
=
=
∑
()
,..........
,.
,......
ax
gx ax x
ax
δ
δ
δ
δ
δ
δ
>
=−≤≤
−<−
⎧
⎪
⎨
⎪
⎩
() ()
() ()
2
2
g
yfydy
g
yfydy
ξ
∞
−∞
∞
−∞
′
=
⎡⎤
⎣⎦
∫
∫
()
(
)
()
gx
fx
f
x
=−
′
()
2
2
........................
2
.............
2
ax
x
x
a
ax x
δ
ρ
δ
δ
δ
≤
=
−>
⎧
⎪
⎨
⎪
⎩
()()
()
2
L
pC a a
a
π
δ
δ
=Φ−Φ−
()
2
2
1
2
y
x
x
edΦ=
∫
y
π
−
−∞
(
)
{
}
t
IhII
=
∇⋅ ∇ ∇
G
∇
a
δ
δδδ δ
∞
−−− −
==
∫
G
(
)
min
I
Id
ρ
Ω
∇
Ω
∫
()
t
I
II
I
ρ
∇
′
=∇⋅ ∇
∇
⎧
⎫
⎨
⎬
⎩⎭
G
()
()
()
..................
sgn
....
ax
x
x
x
x
ak x
x
h
δ
ρ
δ
≤
′
==
>
⎧
⎪
⎨
⎪
⎩
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
426

3.2 Amplitude-Limited Myriad Filter
Similarly, the myriad filter which is the MLE of
location under heavier-tailed Cauchy distributed
noise is defined as
(18)
The behavior of the myriad filter is determined by
the value of
k
, which is called the linearity
parameter. Given a set of samples
12
,,,
M
x
xx
⋅
⋅⋅
,
the sample myriad
ˆ
k
β
in Eq. (18) converges to
sample mean
ˆ
μ
in Eq. (4), as
k
(Gonzalez,
Arce, 2001). It is proposed in this paper that outliers
which are samples outside the region
(
→∞
)
,
δ
δ
−
, are
limited, as shown in Eq. (9). That is, the sample
myriad is computed as
(19)
where
()
g
⋅
is as given in Eq. (9). This filter is
named an amplitude-limited myriad filter (ALMF).
Its sample myriad
ˆ
k
γ
results in amplitude-limited
sample average
ˆ
δ
θ
depicted in Eq. (8), as
.This can be easily proved in the same way
as the myriad filter converges to a mean filter as
as given in (Gonzalez, Arce, 2001).
k →∞
k →∞
3.3 Filtering Scheme
As mentioned above, if the given image pixel is
known to belong to one of the smooth regions
Gaussian noise can be reduced by a mean filter This
filter, however, tends to degrade the sharpness of the
boundaries between regions of an image if it belongs
to the boundary regions. This problem can be
reduced effectively by the ALSAF, which however,
produces visually grainy output as the amount of
impulsive noise increases. Thus, our proposed
approach utilizes the statistics of the samples in the
window. The parameter in Eq. (19).is determined
according to the presence of impulsive noise in the
window.
k
3.3.1 Processing of Impulsive Noise
Deciding which pixels in an image are replaced with
impulsive noise is not clearly defined yet. Especially
in cases they are also corrupted with Gaussian noise,
the problem will be very complicated. Fortunately,
image pixel values does not vary severely from its
surrounding pixels even in the boundary regions.
Thus, each pixel isolated with its neighbors is
detected as an impulse-like pixel.
()
()
2
2
1
In order to decide how impulse-like each pixel is,
the pixels within the window are arranged in the
ascending order for each pixel location, and it is
decided whether the pixel is located at some
predefined range as given in Eq. (20),
[
]
[
]
{
}
,
0,
1,
iii
l
i
xww
D
otherwise
∈
⎧
=
⎨
⎩
u
(20)
where
[
]
i
k
w
is the k th-order statistics of the
samples in the window of size , that is
2N +1
[
]
[
]
[
]
12 2
ii i
N
ww w
+
≤≤⋅⋅⋅≤
1
lN u N
(21)
and and are such that
l u
1121
≤
≤+≤≤ +
i
. If
D
corresponding
to the pixel
i
x
equals 0, then the ALSAF or ALMF
with a large value of is applied to the samples in
the window because it is more probable the pixel
belongs to smooth regions. However, when
k
1
i
D
=
,
the pixel is regarded as impulse-like if the mean of
absolute values of its neighbour differences (MAD),
as given in Eq. (22) is above the predefined
threshold,
x
M
AD x y
∈Ω
=
−
∑
(22)
where is the center pixel and
Ω
is the set of its
neighbors. It is verified experimentally to be a good
indicator of impulsive noise. Its idea is borrowed
from (Garnett, et al., 2005). Fig. 1 and Fig. 2 depict
mean MAD values on whole image pixels as
functions of types of noise and its amount. Impulsive
noise pixels have much larger mean MAD values
than the uncorrupted pixels or the pixels corrupted
with Gaussian noise. When impulsive noise exists at
some pixel in Lena image, its mean MAD value is
y
ˆ
ki
β
arg min
M
i
kx
β
β
=
= +−
∏
()
()
(
)
2
2
1
ˆ
arg min
M
ki
i
kgx
β
γ
γ
=
= +−
∏
OPTIMAL NONLINEAR IMAGE DENOISING METHODS IN HEAVY-TAILED NOISE ENVIRONMENTS
427
127, which does not vary with the amount of
Gaussian noise. In our method, the image pixels
whose MAD values exceed 80 are classified as
impulsive noise. The pixels decided to be impulse-
like are separated to process with an ALMF, whose
parameter as given in Eq. (19) is small. In case
there is no impulse within the window,
k
is set to a
large value so that the ALMF may function as an
ALSAF.
k
Figure 1: Mean MAD values as a function of standard
deviation of Gaussian noise.
Figure 2: Mean MAD values as a function of probability
of impulsive noise.
4 EXPERIMENTAL RESULTS
The widely used gray-scale Lena image is selected
to test our proposed method. Impulsive noise as well
as Gaussian noise are injected to the test image. In
other words, the pixel corrupted with Gaussian noise
is replaced randomly with impulse, which has the
value of 0 (“black”) or 255(“white”) with equal
probability. Simulations are carried out for a wide
range of noise density levels. The performance of
our denoising filter is evaluated by way of mean-
square-error (MSE) metric and peak signal-to-noise
ratio (PSNR) given by
(23)
where
e
σ
is the standard deviation of the residual
errors
(24)
()
2
1
ˆ
ei
i
i
x
x
σ
∈Ω
=−
Ω
∑
In the above equation,
Ω
represents the number of
pixels in the image.
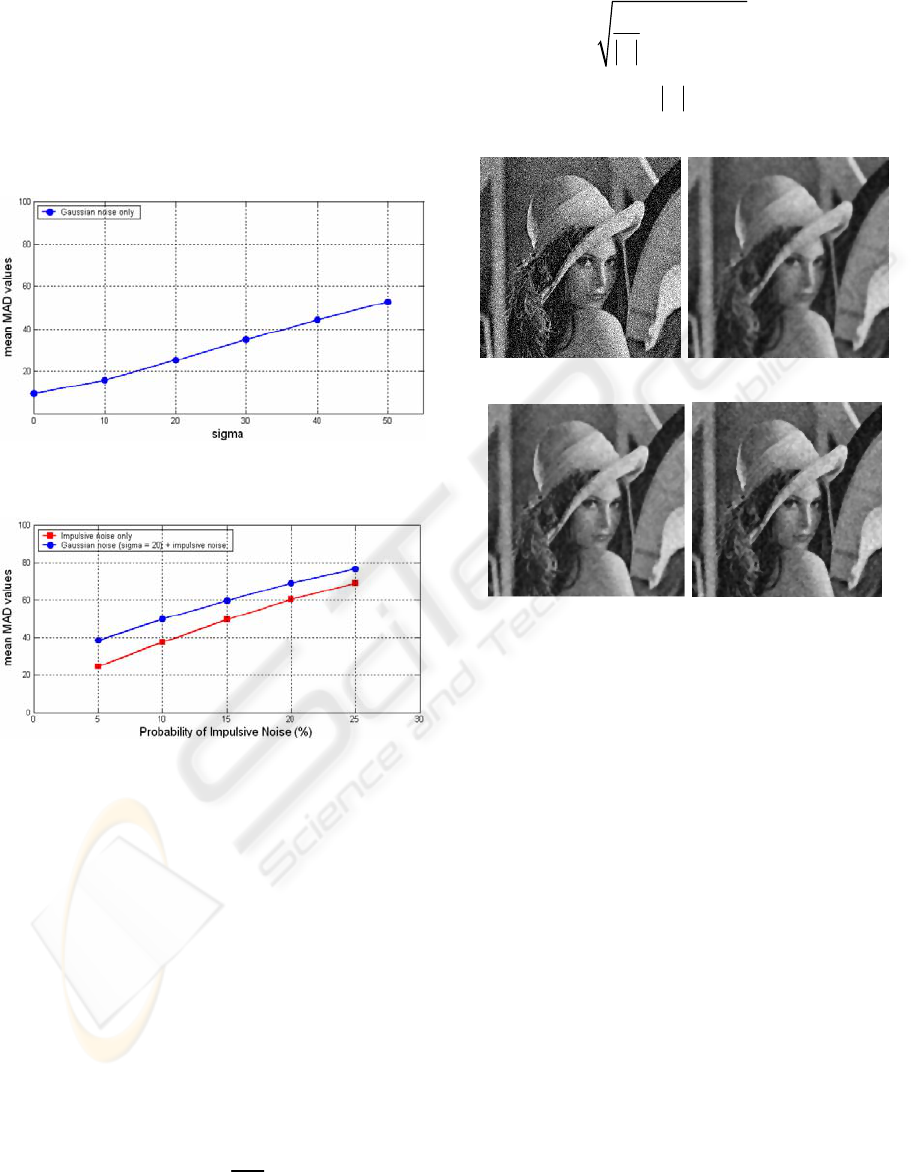
(a) (b)
(c) (d)
Figure 3: (a) Corrupted Lena image degraded by Gaussian
noise of variance , with a measured
2
924
n
σ
=
18.5
P
SNR dB
=
(b) PM anisotropic diffused image after
10 iterations with and
2
153.3
n
σ
=
26.3
P
SNR dB=
(c) Output of the ALSAF after 10 iterations with
and
2
137.6
n
σ
=
26.8
P
SNR dB
=
(d) Output of the
ALMF with and
2
155.2
n
σ
=
26.2
P
SNR dB=
.
Fig. 3 shows the simulation results when gray scale
image of size
256 256
×
is corrupted with additive
Gaussian noise of variance
n
2
924
σ
=
)(20
P
SNR dB
=
. Obviously, both our methods
suppress additive Gaussian noise without severely
destroying the fine details compared with PM
equation in spite of the fact that there are no
significant differences in their PSNR values.
Simulation results are depicted in Fig. 4 when the
Lena image is corrupted with both Gaussian noise of
variance
2
and 10% of impulsive noise
900
σ
=
(20PSNR dB)
=
. Simulation results show that the
ALSAF is not effective in removing impulsive noise,
while the myriad filter can be extended to reduce
10
255
20log
e
PSNR
σ
=
⎛⎞
⎜⎟
⎝⎠
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
428

both Gaussian and impulsive noise by limiting the
amplitude of samples outside predefined range as
given in Eq. (9). This ALMF tends to preserve the
fine details while reducing both Gaussian and
impulsive noise.
(a) (b)
(c) (d)
Figure 4: (a) Lena image corrupted with both Gaussian
noise of
30
σ
=
and impulsive noise of
10%
p
=
,
with a measured residual variance and
2
2059.3
n
σ
=
15.0
P
SNR dB=
, (b) Output of the ALSAF after 10
iterations with and
2
359.6
n
σ
=
22.6
P
SNR dB=
(c)
Output of myriad filter with and
2
557.9
n
σ
=
20.67
P
SNR dB=
(d) Output of ALMF with
and
2
234.7
n
σ
=
24.42
P
SNR dB=
.
5 CONCLUSIONS
Optimal nonlinear filter which maximizes the
efficacy under mixed Gaussian noise environment is
derived. This filter effectively can be implemented
using PM anisotropic diffusion by selecting the
appropriate edge stopping function. However, it
produces visually grainy output as the amount of
impulsive noise increases. Thus, impulse-like signal
detection is introduced to process impulsive pixels
differently from the remaining pixels. For this
process, a myriad filter is selected, which is a
maximum log-likelihood estimator of the location
parameter for Cauchy density. The filter is known to
outperform median-based filters in removing
impulsive noise. By combining ALSAF which is a
MLE in mixed Gaussian noise with a myriad filter,
the resulting filter (ALMF) effectively removes both
Gaussian and impulsive noise, preserving the fine
details.
REFERENCES
Rabie, T., 2005. Robust Estimation Approach for Blind
Denoising. IEEE Trans. Image Process., vol. 14, No.
11, pp. 1755-1765.
Black, M. J., Sapiro, G., Marimont, D. H., 2005. Robust
Anisotropic Diffusion. IEEE Trans. Image Process.,
vol. 14, No. 11, pp.421-432.
Huber, P., 1981. Robust Statistics, New York: Wily.
Perona, P., Malik, J., 1990. Scale-Space and Edge
Detection Using Anisotropic Diffusion. IEEE Trans.
PAMI, vol. 12, No. 7, Jul., pp. 629-639.
Hamza, A. B., Krim, H., 2001. Image Denoising: A
Nonlinear Robust Statistical Approach. IEEE Trans.
Signal Process., vol.49, No.12, pp.3045-3054.
Garnett, R., Huegerich, T., Chui, C., He, W., 2005. A
Universal Noise Removal Algorithm With an Impulse
Detector. IEEE Trans. Image Process., vol. 14, No. 11,
pp. 1747-1754.
Gonzalez, J. G., Arce, G. R., 2001. Optimality of the
Myriad Filter in Practical Impulsive-Noise
Environments. IEEE Trans. Signal Process., vol.49,
No.2, pp. 438-441.
Zurbach, P., Gonzalez, J. G., Arce, G. R., 1996. Weighted
Myriad Filters for Image Processing. ICIP96, pp. 726-
728.
OPTIMAL NONLINEAR IMAGE DENOISING METHODS IN HEAVY-TAILED NOISE ENVIRONMENTS
429
