CUED SPEECH HAND SHAPE RECOGNITION

Belief Functions as a Formalism to Fuse SVMs & Expert Systems

Thomas Burger, Alexandra Urankar

France Telecom R&D, 28 ch. Vieux Chêne, Meylan, France

Oya Aran, Lale Akarun

Dep. of Comp. Eng., Bogazici University, Bebek 34342, Istanbul, Turkey

Alice Caplier

LIS, Institut National Polytechnique de Grenoble, 46 av. Felix Viallet, Grenoble, France

Keywords: Support Vector Machine, Expert systems, Belief functions, Hu invariants, Hand shape and gesture

recognition, Cued Speech.

Abstract: As part of our work on hand gesture interpretation, we present our results on hand shape recognition. Our

method is based on attribute extraction and multiple binary SVM classification. The novelty lies in the

fashion the fusion of all the partial classification results are performed. This fusion is (1) more efficient in

terms of information theory and leads to more accurate result, (2) general enough to allow other source of

information to be taken into account: Each SVM output is transformed to a belief function, and all the

corresponding functions are fused together with some other external evidential sources of information.

1 INTRODUCTION

Hand shape recognition is a widely studied topic

which has a wide range of applications such as HCI

(Pavlovic, 1997), automatic translators, tutoring

tools for the hearing-impaired (Ong, 2005), (Aran,

2005), augmented reality, and medical image

processing.

Even if this field is dominated by Bayesian

methods, several recent works deal with evidential

methods, as they bring a certain advantage in the

fashion uncertainty is processed in the decision

making (Quost, 2007), (Capelle, 2004).

The complete recognition of a hand shape with

no constraint on the shape is an open issue. Hence,

we focus on the following problem: (1) the hand is

supposed to roughly remain in a plan which is

parallel to the acquisition plan (2) only nine different

shapes are taken into account (Figure 1a). On the

contrary, no assumption is made on the respective

location of the fingers (whether they are gathered or

not) except for hand shapes 2 (gathered fingers) and

8 (as separated as possible), as this is their only

difference. These nine hand shapes correspond to the

gesture set used in Cued Speech (Cornett, 1967).

(a) Artificial representation of the hand shape classes.

(b) Segmented hand shape examples from real data

Figure 1: The 9 hand shape classes.

There are many methods already developed to

deal with hand modeling and analysis. For a

complete review, see (Derpanis, 2004), (Wu, 2001).

In this paper, we do not develop the segmentation

aspect. Hence, we consider several corpuses of

binary images such as in Figure 1b, as the basis of

our work. The attribute extraction is presented in

Burger T., Urankar A., Aran O., Akarun L. and Caplier A. (2007).

CUED SPEECH HAND SHAPE RECOGNITION - Belief Functions as a Formalism to Fuse SVMs & Expert Systems.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 5-12

 SciTePress

Section 2. The required classification tools are

presented in Section 3. Section 4 is the core of this

paper: we apply the decision making method, which

is theoretically presented in (Burger, 2006), to our

specific problem, and we use its formalism as a

framework in which it is possible to combine

classifiers of various nature (SVMs and expert

systems) providing various partial information.

Finally, Section 5 provides experimental results.

2 ATTRIBUTE DEFINITION

2.1 Hu Invariants

The dimensionality of the definition space for the

binary images we consider is too large, and it is

intractable to use pixel coordinates in that space to

perform the classification. One needs to find a more

compact representation of the information contained

in the image. Several such binary image descriptors

are to be found in the image compression literature

(Zhang, 2003). They can be classified into two main

categories:

 Region descriptors, which describe the binary

mask of a shape, such as Zernike moments, Hu

invariants, grid descriptors…

 Edge descriptors, which describe the closed

contour of the shape, such as Fourier descriptors,

Curvature Scale Space (CSS) descriptors…

Region descriptors are less sensitive to edge

noise because of an inertial effect of the region

description. Edge descriptors are more related to the

way human compare shapes.

A good descriptor is supposed to obey several

criteria, such as several geometrical invariance,

compactness, being hierarchical (so that the

precision of the description can be truncated), and be

representative of the shape.

We focus on Hu invariants, which are successful

in representing hand shapes (Caplier, 2004). Their

purpose is to express the mass repartition of the

shape via several inertial moments of various orders,

on which specific transforms ensure invariance to

similarities.

Let us compute the classical definition of

centered inertial moments of order p+q, for the

shape (invariant to translation, as they are centered

on the gravity center):

(

)

(

)

(, )

mxxyyxydxdy

=− −

∫∫

(1)

With

and

being the coordinates of the

gravity center of the shape and

(, ) 1xy

if the

pixel belongs to the hand shape and 0 otherwise. In

order to make these moments invariant to scale, we

normalize them:

(2)

Then, we compute the six Hu invariants, which

are invariant to rotation, and mirror reflection:

()

()()

( )()()()

()

( )()()()

()

()()()

()

()()

210312

2103

02206

2103

21032103

2103

02202

02201

nnnnn

nnnnnnS

nnnnnnnn

nnnnnnnnS

nnnnS

nnnS

nnS

+⋅+⋅⋅+

+−+⋅+=

+−+⋅⋅+⋅⋅−−

+⋅−+⋅+⋅⋅−=

+++=

⋅−+⋅−=

⋅++=

(3)

A seventh invariant is available. Its sign permits

to discriminate mirror images and thus, to suppress

the reflection invariance:

(

)

(

)

(

)( )

(

)

()()()()

(

)

2103

21031230

2103

03217

3..3

nnnnnnnn

nnnnnnnnS

+++⋅⋅+⋅⋅−−

+⋅−++−⋅=

(4)

The reflection invariance has been removed at

the acquisition level and only left hands are

processed. Hence, we do not need to discriminate

mirror images. We nevertheless use S

as both the

sign and the magnitude carry information: it

sometimes occurs that hand shapes 3 and 7 (both

with separated fingers) really look like mirror

images. Finally, the attributes are:

, S

2.2 Thumb Presence

The thumb is an easy part to detect, due to its

peculiar size and position with respect to the hand.

Moreover, the thumb presence is a very

discriminative piece of evidence as three hand

shapes require the thumb and six do not require it.

The thumb detector works as follows:

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

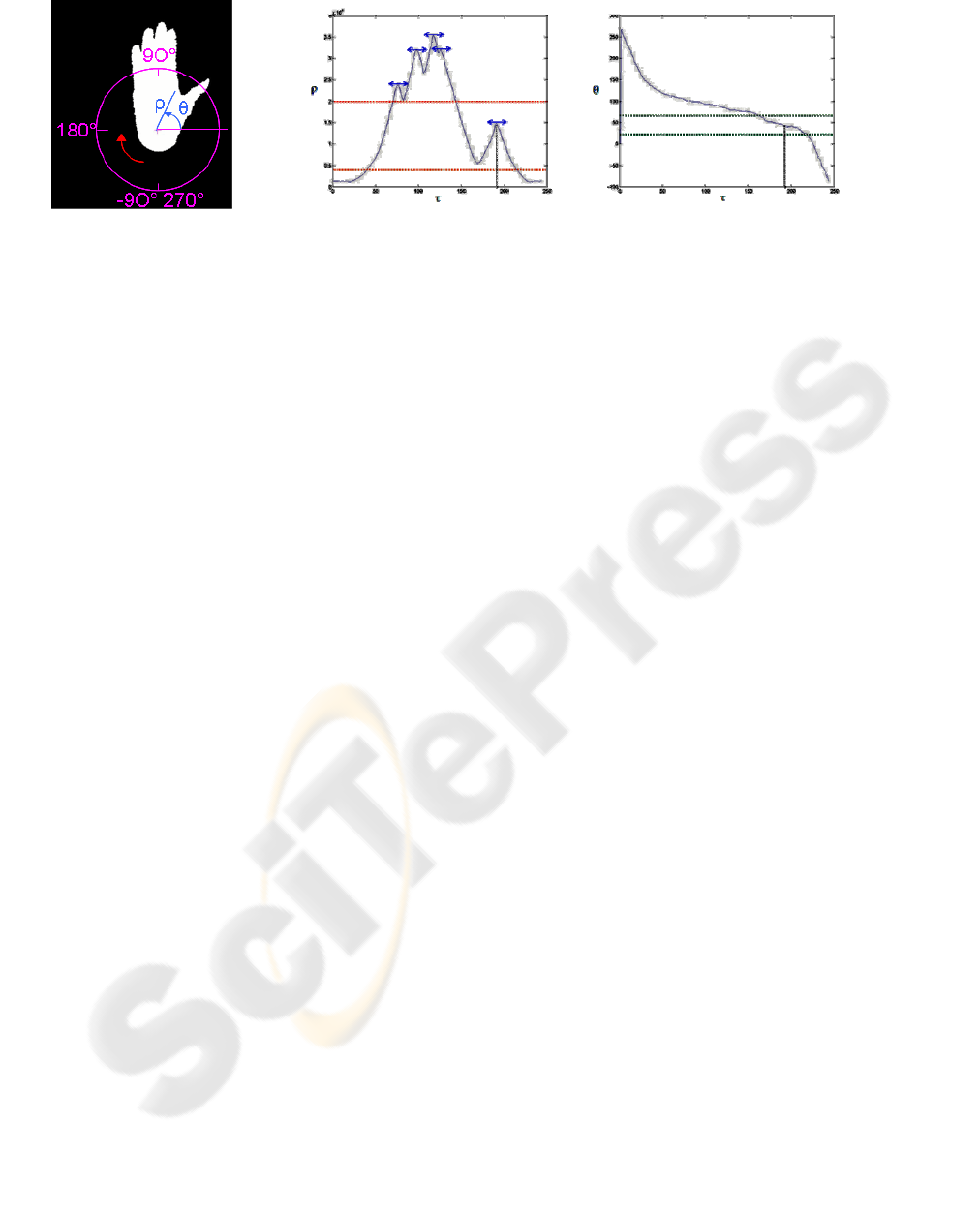
Figure 2: Thumb detection.

(1) Polar parametric definition: By following the

contour of the hand shape, a parametric

representation {ρ(

τ), θ(τ)} is derived in polar

coordinates (Figure 2)

(2) Peak detection: After smoothing the

parametric functions, (low-pass filtering and sub-

sampling), the local maxima of the ρ function are

detected. Obviously, they correspond to the potential

fingers (Figure 2b).

(3) Threshold adaptation: Thresholds must be

defined on the distance and the angle values to

indicate the region in which a thumb is plausible.

The angle thresholds that describe this region are

derived from morphological statistics (Norkin,

1992). In practice, the thumb angle with respect to

the horizontal axis (Figure 2b) is between 20° and

65°. The distance thresholds are derived from a basic

training phase whose main purpose is to adapt the

default approximate values (1/9 and 5/9 of the hand

length) via a scale normalization operation with

respect to the length of the thumb. Even if the

operation is simple, it is mandatory to do so, as the

ratio of the thumb length with respect to the total

hand length varies from hand to hand.

(4) Peak measurement: If a finger is detected in

the area defined by these thresholds, it is the thumb.

Its height with respect to the previous local minima

(Figure 2) is measured. It corresponds to the height

between the top of the thumb and the bottom of the

inter-space between the thumb and the index. This

value is the thumb presence indicator (it is set to

zero when no thumb is detected). In practice, the

accuracy of the thumb detection (the thumb is

detected when the corresponding indicator has a

non-zero value) reaches 94% of true detection with

2% of false alarms.

The seven Hu invariants and the thumb presence

indicator are used as attributes for the classification.

3 CLASSIFICATION TOOLS

3.1 Belief Functions

In this section, we briefly present the necessary

background on belief functions. For deeper

comprehension of these theories, see (Shafer, 1976)

and (Smets, 1994).

Let Ω be the set of N exclusive hypotheses

…h

. We call Ω the frame. Let m(.) be a belief

function on 2

Ω

(the powerset of Ω) that represents

our mass of belief in the propositions that

correspond to the elements of 2

Ω

[

]

:2 0,1m

→

()with () 1

AmA mA

⊆Ω

∑



(5)

Note that:

 Belief can be assigned to non-singleton

propositions, which allows modeling the hesitation

between elements;

 Ø belongs to 2

Ω

. A belief in Ø corresponds to

conflict in the model, throughout an assumption in

an undefined hypothesis of the frame or throughout

a contradiction between the information on which

the decision is made.

To combine several belief functions (each

associated to one specific captor) into a global belief

function (under associativity and symmetry

assumptions), one uses the conjunctive combination.

For N belief functions, m

…m

, defined on the same

frame Ω, the conjunctive combination is defined as:

12 ()

: ...

...

mm m m

ΩΩ Ω

(∩) (∩) (∩)

(∩) × × × →

∩







BB B B

(6)

(a) Binary hand shape

image.

(b) Hand polar parametric representation along the curvilinear abscissa τ (distance ρ and

angle θ). The thumb is within a peculiar distance and angle range (horizontal lines).

CUED SPEECH HAND SHAPE RECOGNITION - Belief Functions as a Formalism to Fuse SVMs & Expert Systems

with

Ω

being the set of belief functions defined on

Ω and m

(

∩

)

being the global combined belief

function. Thus, m

(

∩

)

is calculated as:

() ( )

()

...

AA A

mA mA A

=∩∩

⎛⎞

=∀⊆

⎜⎟

⎝⎠

∑

∏

∩

(7)

The conjunctive combination means that, for

each element of the power set, its belief is the

combination of all the beliefs (from the N sources)

which imply it: the evidential generalization of the

logical AND.

After having fused several beliefs, the knowledge

in the problem is modeled via a function over 2

Ω

which expresses the potential hesitations in the

choice of the solution. In order to provide a

complete decision, one needs to eliminate this

hesitation. For that purpose, we use the Pignistic

Transform (Smets, 1994), which maps a belief

function from 2

Ω

onto Ω, on which a decision is easy

to make. The Pignistic Transform is defined as:

()

Ω∈∀

/−

∑

Ω⊂∈

AAh ,

)BetP(

(8)

where A is a subset of Ω, or equivalently, an element

of 2

Ω

, and |A| its cardinal when considered as a

subset of Ω.

This transform corresponds to sharing the

hesitation between the implied hypotheses, and

normalizing the whole by the conflictive mass.

As an illustration of all these concepts, let us

consider a simple example. Assume that we want to

automatically determine the color of an object. The

color of the object can be one of the primary colors:

red (R), green (G) or blue (B). The object is

analyzed by two sensors of different kind, any of

each giving an assumption of its color.

Table 1: Numerical example for belief function use.

∅

{R, G}

{R, B}

{B, G}

{R, G, B}

0 0.5 0 0 0.5 0 0 0

0 0 0 0 0 0 0.4 0.6

(∩) m

0.2 0.3 0.2 0 0.3 0 0 0

BetP

0.56

0.44 0 0 0 0 0

The observations of the sensors are

expressed as belief functions m

(.) and m

(.) and the

frame is defined as Ω

color

= {∅, R, G, B, {R, G}, {R,

B}, {B, G}, {R, G, B}} representing the hypothesis

about the color of the object. Then, they are fused

together into a new belief function via the

conjunctive combination. As the object has a single

color, the belief in union of colors is meaningless

from a decision making point of view. Hence, one

applies the Pignistic Transform on which a simple

argmax decision is made. This is summarized and

illustrated with numerical values in

Table 1.

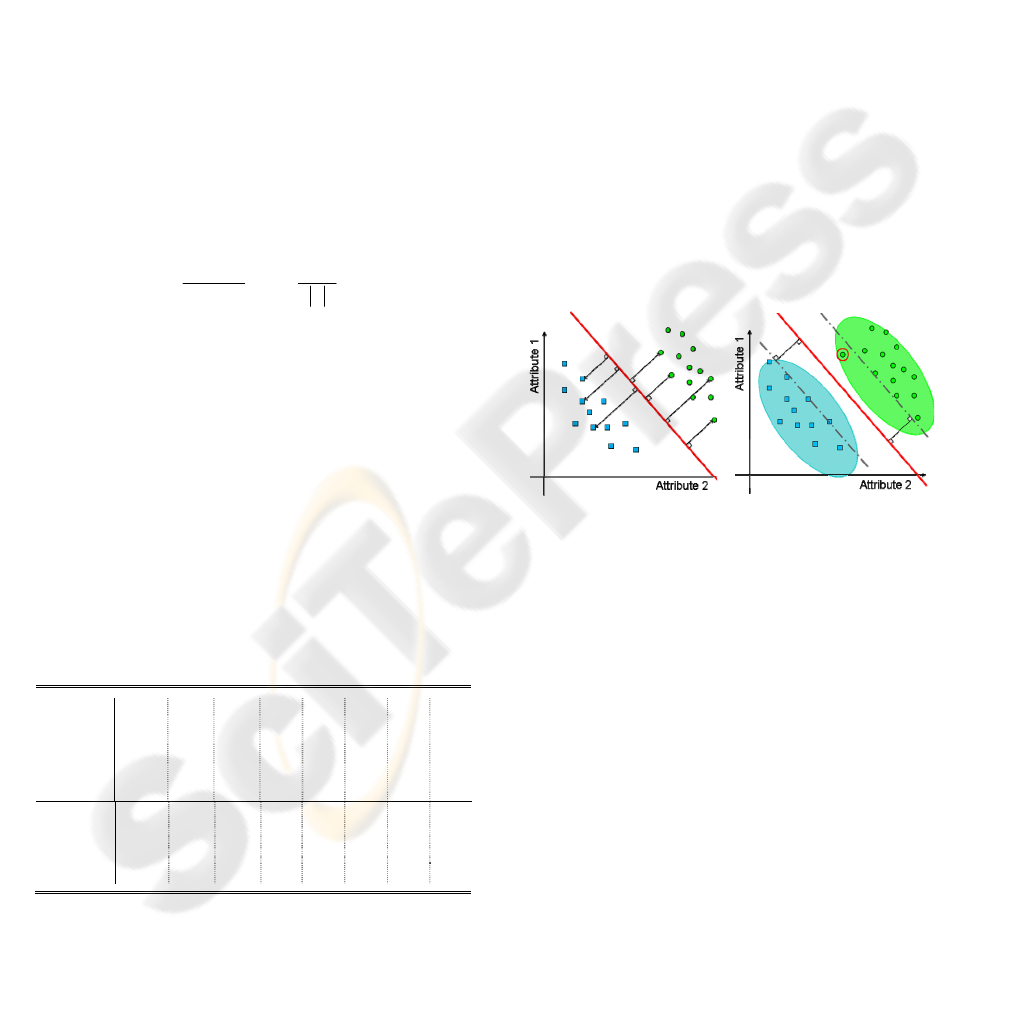
3.2 Support Vector Machines

SVMs (Boser, 1995), (Cortes, 1995) are powerful

tools for binary classification. Their purpose is to

materialize the correlation of the attributes for each

class by defining a separating hyperplane derived

from a training corpus, which is supposed to be

statistically representative of the classes involved.

The hyperplane is chosen among all the possible

hyperplanes through a complex combinatorial

problem optimization, so that it maximizes the

distance (called the margin) between each class and

the hyperplane itself (Figure 3a & Figure 3b).

(a) (b)

Figure 3: (a) combinatorial optimization of the hyperplane

position under the constraints of the training corpus item

positions. (b) The SVM provides good classification

despite the bias of the training.

To deal with the nine hand shapes in our

database, a multiclass classification with SVMs must

be performed. As SVMs are restricted to binary

classification, several strategies are developed to

adapt them for multiclass classification problems

(Hsu, 2002). For that purpose, we have developed a

scheme (Burger, 2006) which fuses the outputs of

the SVMs using the belief formalism, and which

provides a robust way of dealing with uncertainties.

The method can be summarized by the following

three steps:

(1) 36 SVMs are used to compare all the possible

class pairs among nine classes;

(2) A belief function is associated to each SVM

output, to model the partial knowledge brought by

the corresponding partial binary classification;

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

(3) The belief functions are fused together with a

conjunctive combination, in order to model the

complete knowledge of the problem, and to make a

decision according to its value.

4 DECISION SCHEME

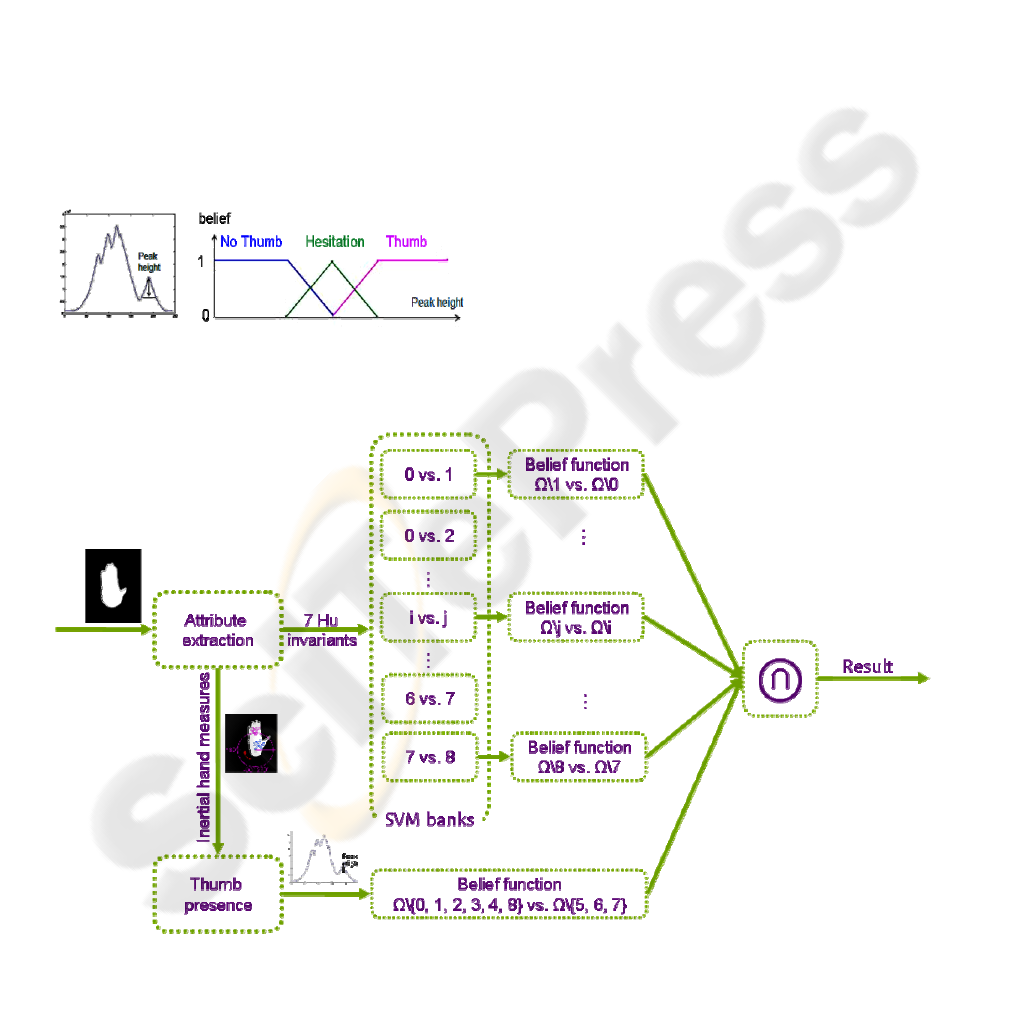
4.1 Belief in the Thumb Presence

In order to fuse the information from the thumb

presence indicator with the output of the SVM

classifier, one needs to express it throughout a belief

function. As it is impossible to have a complete

binary certitude on the presence of the thumb (it is

possible to be misled at the thumb detection stage as

explained previously), we use a belief function

which authorizes hesitation in some cases.

(a) (b)

Figure 4: (a) The peak height determines (b) the belief in

the presence of the thumb.

From an implementation point of view, we use a

technique based on fuzzy sets, as explained in Figure

4: The higher the peak of the thumb is, the more

confident we are in the thumb presence. This process

is fully supported by the theoretical framework of

belief functions, as the set of the finite fuzzy sets

defined on Ω is a subset of

Ω

(the set of belief

functions defined on Ω). Moreover, as belief

functions, fuzzy sets have peculiar properties which

make them really convenient to fuse with the

conjunctive combination (Denoeux, 2000).

The three values that define the support of the

hesitation in Figure 4b have been manually fitted

according to observations on the training set.

Making use of the "fuzziness" of the threshold

between the thumb presence and absence, these

values are not necessarily precisely settled. In

practice, they are defined via three ratios (1/5, 1/20

and 1/100) of the distance between the center of

palm and the furthest element from it of the contour.

Then, the belief in the presence of the thumb can

be associated to a belief in some hand shapes to

produce a partial classification: In hand shapes 0, 1,

2, 3, 4, and 8, there is no thumb, whereas it is visible

for shapes 5, 6 and 7. In case of hesitation in the

thumb presence, no information is brought and the

belief is associated to Ω.

Figure 5: Global fusion scheme for hand shape classification.

CUED SPEECH HAND SHAPE RECOGNITION - Belief Functions as a Formalism to Fuse SVMs & Expert Systems

4.2 Partial Classification Fusion

Thanks to the evidential formalism, it is possible to

fuse partial information from various classifiers (36

SVMs and 1 expert system) through the conjunctive

combination (Figure 5). In that fashion, it is possible

to consider a SVM-based system and integrate it into

a wider data fusion system.

This fusion provides a belief function over the

powerset 2

Ω

of all the possible hand shapes Ω. This

belief is mapped over Ω via the Pignistic Transform,

to express our belief in each singleton element of Ω.

Then, the decision is made by an argmax function

over Ω.

()

argmax BetP(.)D

(9)

5 RESULTS

In this section, we present various results on the

methodology described above. In the first paragraph,

the database and the evaluation methods are

detailed. In the second paragraph, the experiments

and their corresponding results are given.

5.1 Database & Methodology

The hand shape database used in this work is

obtained from Cued Speech videos. The transition

shapes are eliminated manually and the remaining

shapes are labeled and used in the database as binary

images representing the 9 hand shapes (Figure 1).

Table 2: Details of the database.

Hand Shape

Corpus 1

(Training set)

Corpus 2

(Test set)

37 12

94 47

64 27

84 36

72 34

193 59

80 46

20 7

35 23

Total

679 291

The training and test sets of the database are

formed such that there is no strict correlation

between them. To ensure this, two different corpuses

are used in which a single user is performing two

completely different sentences using Cued Speech.

The respective distribution of the two corpuses is

given in Table 2. The statistical distribution of the

hand shapes is not balanced at all within each

corpus. The reason of such a distribution is related to

the linguistics of Cued Speech, and is beyond our

scope.

For all the experiments, Corpus 1 is used as the

training set for the SVMs and Corpus 2 is used as

the test set. As for each image, since the real labels

are known, we use the classical definition of the

accuracy to evaluate the performance of the

classifier:

Νumber Οf Well Classified Items

100

Τotal Νumber Οf Ιtems

Accuracy =⋅

(10)

To fairly quantify the performances of each

classification procedure, two indicators are used: (1)

The difference between the respective accuracies,

expressed in a number of point ΔPoint, and (2) the

percentage of avoided mistake %AvMis:

(

)()

2_1Point Accuracy Method Accuracy MethodΔ= −

()

Number of Avoided Mistakes

% 100

Total Number of Mistakes

100

100 _1

AvMis

Point

Accuracy Method

=⋅

−

(11)

5.2 Experiments

The goal of the first experiment is to evaluate the

advantage of the evidential fusion for the SVM.

Thus, we compare the classical methods for SVM

multi-classification to the one of (Burger, 2006). For

both of the methods, the training is the same and the

SVMs are tuned with respect to the training set and

the thumb information is not considered.

For the implementation of the SVM functionalities,

we use the open source C++ library LIBSVM

(Chang, 2001). We use:

 C-SVM, which is a particular algorithm to

solve the combinatorial optimization. The cost

parameter is set to 100,000 and termination criteria

to 0.001.

 Sigmoid kernels in order to transform the

attribute space so that it is linearly separable:

(

)

(,) tanh

with 0.001 and 0.25

Ker u v u v R

=⋅⋅+

==−

(12)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

For the evidential method, we have made various

modifications on the software so that the SVM

output is automatically presented throughout the

evidential formalism (Burger, 2006). These

modifications are available on demand.

The results are presented in Table 3, as the test

accuracy of the classical voting procedure and the

default tuning of the evidential method. The

improvement in ΔPoint is worth 1.03 points and

corresponds to an avoidance of mistakes of

%AvMis = 11.11%.

Table 3: Results for experiments 1 & 2.

Evidential method

Classical

Voting

procedure

Default

(no thumb

detection)

With Thumb

Detection

Test

Accuracy

90.7% 91.8% 92.8%

The goal of the second experiment is to evaluate

the advantage of the thumb information. For that

purpose, we add the thumb information to the

evidential method. Thus, the training set is used to

set the two thresholds, which defines the possible

distance with respect to the center of palm.

However, the thumb information is not used during

the training of the SVMs as they only work on the

Hu invariants, as explained in Figure 5. The results

with and without the thumb indicator are presented

in Table 3.

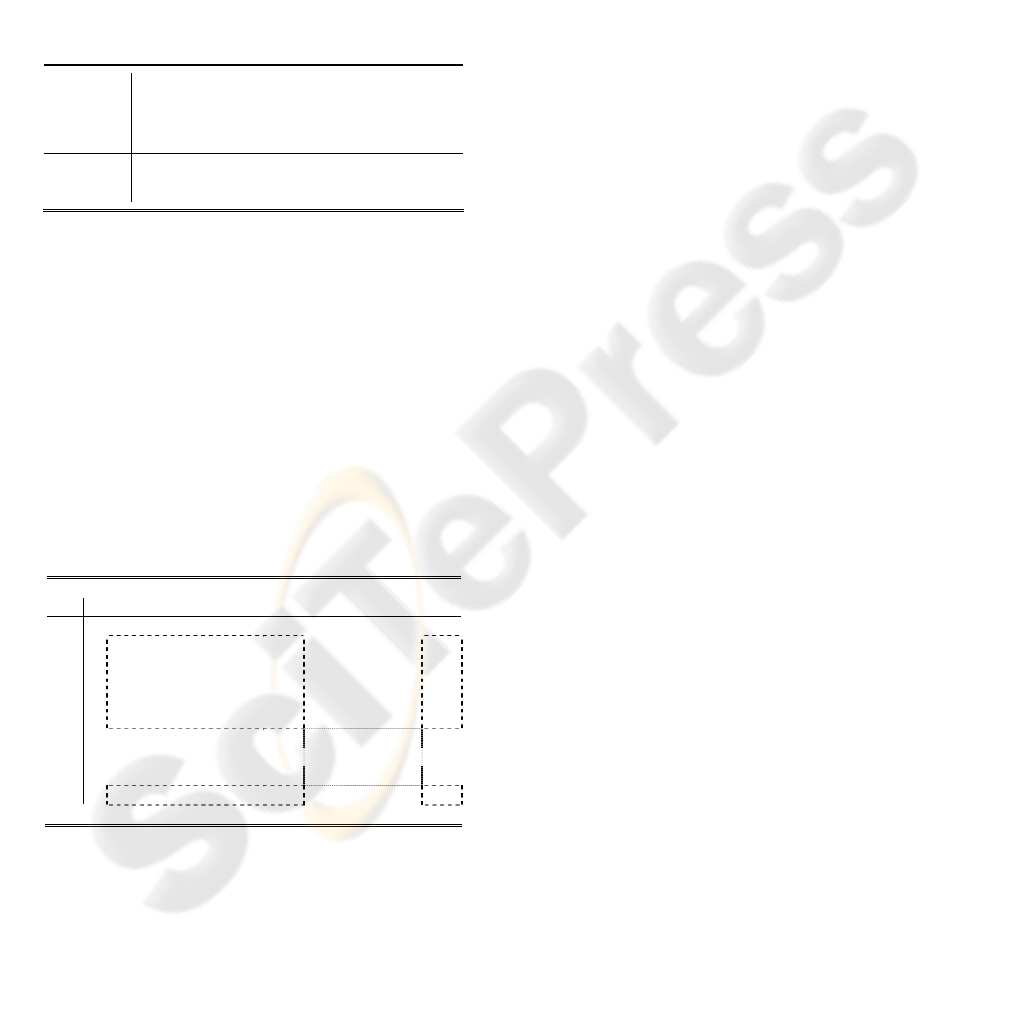
Table 4: Confusion matrix for the second method on

Corpus 2, with the Thumb and NoThumb superclasses

framed together.

0 1 2 3 4 5 6 7 8

12 0 0 0 0 0 0 0 0

0 46 0 0 0 0 0 0 1

0 2 23 2 0 0 0 0 0

0 2 0 29 2 2 1 0 0

0 0 0 1 32 0 0 0 1

0 0 0 0 0 58 0 1 0

0 0 2 0 0 0 41 3 0

0 0 0 0 0 0 1 6 0

0 0 0 0 0 0 0 0 23

The evidential method that uses the thumb

information provides an improvement of 2.06 points

with respect to the classical voting procedure, which

corresponds to an avoidance of 22.22% of the

mistakes. Table 4 presents the corresponding

confusion matrix for the test set: Hand shape 3 is

often misclassified into other hand shapes, whereas,

on the contrary, hand shape 1 and 7 gather a bit

more misclassification from other hand shapes.

Moreover, there are only three mistakes between

THUMB and NO_THUMB super-classes.

6 CONCLUSION

In this paper, we propose to apply a belief-based

method for SVM fusion to hand shape recognition.

Moreover, we integrate it in a wider classification

scheme which allows taking into account other

sources of information, by expressing them in the

Belief Theories formalism. The results are better

than with the classical methods (more than 1/5 of the

mistakes are avoided) and the absolute accuracy is

high with respect to the number of classes involved.

ACKNOWLEDGEMENTS

This work is the result of a cooperation supported by

SIMILAR, European Network of Excellence

(www.similar.cc).

REFERENCES

Aran, O., Keskin, C., Akarun, L., 2005. Sign Language

Tutoring Tool, EUSIPCO’05, Antalya, Turkey.

Burger , T., Aran, O., and Caplier, A., 2006. Modeling

hesitation and conflict: A belief-based approach, In

Proc. ICMLA.

Boser, B., Guyon, I., and Vapnik, V., 1995. A training

algorithm for optimal margin classifiers, In Proc. Fifth

Annual Workshop on Computational Learning Theory.

Capelle, A. S., Colot, O., Fernandez-Maloigne, C., 2004.

Evidential segmentation scheme of multi-echo MR

images for the detection of brain tumors using

neighborhood information. Information Fusion,

Volume 5, Number 3, pages 203-216.

Caplier, A., Bonnaud, L., Malassiotis, S., and Strintzis,

M., 2004. Comparison of 2D and 3D analysis for

automated Cued Speech gesture recognition,

SPECOM, St Petersburg, Russia.

Chang , C.-C., and Lin, C.-J., 2001. LIBSVM: a library

for support vector machines. Software available at

http://www.csie.ntu.edu.tw/~cjlin/libsvm

Cornett, R. O., 1967. Cued Speech, American Annals of

the Deaf.

Cortes, C., and Vapnik, V., 1995. Support-vector network,

Machine Learning 20, 273–297.

Denoeux, T., 2000. Modeling vague beliefs using fuzzy-

valued belief structures. Fuzzy Sets and Systems,

116(2):167-199.

CUED SPEECH HAND SHAPE RECOGNITION - Belief Functions as a Formalism to Fuse SVMs & Expert Systems

Derpanis, K. G., 2004. A review on vision-based hand

gestures, internal report.

Hsu, C.-W., and Lin, C.-J., 2002. A comparison of

methods for multi-class support vector machines,

IEEE Transactions on Neural Networks, Vol. 13, pp.

415-425.

Norkin, C.C., and Levangie , P.K., 1992. Joint structure

and function. (2nd ed.). Philadelphia: F.A. Davis.

Ong, S.C.W. and Ranganath, S., 2005. Automatic Sign

Language Analysis: A Survey and the Future beyond

Lexical Meaning, IEEE Transactions on Pattern

Analysis and Machine Intelligence, vol. 27, pp. 873-

891.

Pavlovic, V., Sharma ,R. and Huang , T. S., 1997. Visual

Interpretation of Hand Gestures for Human-Computer

Interaction: A Review, IEEE Transactions on Pattern

Analysis and Machine Intelligence, vol. 19, n. 7,

p. 677-695.

Quost, B., Denoeux, T., and Masson, M.-H., 2007.

Pairwise classifier combination using belief functions.

To appear in Pattern Recognition Letters.

Shafer, G., 1976. A Mathematical Theory of Evidence,

Princeton University Press.

Smets, P., and Kennes, R., 1994. The transferable belief

model. Artificial Intelligence, 66(2): 191–234.

Wu, Y., Huang, T.S., 2001. Hand modeling, analysis, and

recognition for vision based Human-Computer

Interaction, IEEE Signal Processing Magazine, v.21,

p.51–60.

Zhang, D., and Lu, G., 2003. Evaluation of MPEG-7 shape

descriptors against other shape descriptors, Multimedia

Systems, vol. 9, issue 1.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications