HUMAN VISUAL PERCEPTION, GESTALT PRINCIPLES AND

DUALITY REGION-CONTOUR

Application to Computer Image Analysis of Human Cornea Endothelium

Yann Gavet, Jean-Charles Pinoli

Centre Ing´enierie et Sant´e & Laboratoire LPMG, UMR CNRS 5148

Ecole Nationale Sup´erieure des Mines, Saint-Etienne, France

Gilles Thuret, Philippe Gain

Facult´e de M´edecine, Saint-Etienne, France

Keywords:

Pattern recognition, segmentation, grouping, cognitive and biologically inspired computer vision, mathemat-

ical morphology, medical image analysis, computational geometry, Gestalt Theory, Contour closure, Mosaic

reconstruction, image analysis.

Abstract:

The human visual system is far more efﬁcient than a computer to analyze images, especially when noise or

poor acquisition process make the analysis impossible by lack of information. To mimic the human visual

system, we develop algorithms based on the gestalt theory principles: proximity and good continuation. We

also introduce the notion of mosaic that we reconstruct with those principles. Mosaics can be deﬁned as

geometry ﬁgures (squares, triangles), or issued from a contour detection system or a skeletonization process.

The application presented here is the detection of cornea endothelial cells. They present a very geometric

structure that give enough information for a non expert to be able to perform the same analysis as the ophthal-

mologist, that mainly consists on counting the cells and evaluating the cell density.

1 INTRODUCTION

Image processing specialists have often the same

problem. People come with their images of their

own domain of excellence, for example in the ﬁeld

of ophthalmology, which is the application frame of

the present paper. They ask for counting the cells in

the corneal endothelium (ﬁg. 1), adding it might not

be difﬁcult because a child could perform it.

If it were so simple, it would be a long time we

should have had to work on another subject. To char-

acterize the quality of the cornea, ophthalmologists

ﬁrst evaluate the cell density and then the shape ir-

regularities of the cells. One method consists on de-

tecting the contours of the cells and then compute the

parameters, like cell density or hexagonality (Gain

et al., 2002; Debayle et al., 2006). Softwares using

the ﬁrst detection method (Gain et al., 2002) are cur-

rently used in biomedical laboratories, but the special-

ists are still not satisﬁed because they have to spend a

few minutes checking and correcting the cell borders,

a work that a child could do (ﬁg. 2).

Figure 1: 215 × 215 pixels (0.036mm

) image of a hu-

man corneal endothelium acquired by specular optical mi-

croscopy. The endothelial cells are theoretically hexago-

nally shaped. The borders appear as dark contour lines on

this image. But sometimes (for example at the bottom left

of the image) the borders are nearly of the same intensity

level as the inside of the cells, so the segmentation of these

cells cannot be only based on the intensity information.

1.1 Theoretical Human Vision

Processing

When there is not enough information about contours

in an image, no algorithm can really detect anything.

221

Gavet Y., Pinoli J., Thuret G. and Gain P. (2007).

HUMAN VISUAL PERCEPTION, GESTALT PRINCIPLES AND DUALITY REGION-CONTOUR - Application to Computer Image Analysis of Human

Cornea Endothelium.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 221-224

 SciTePress

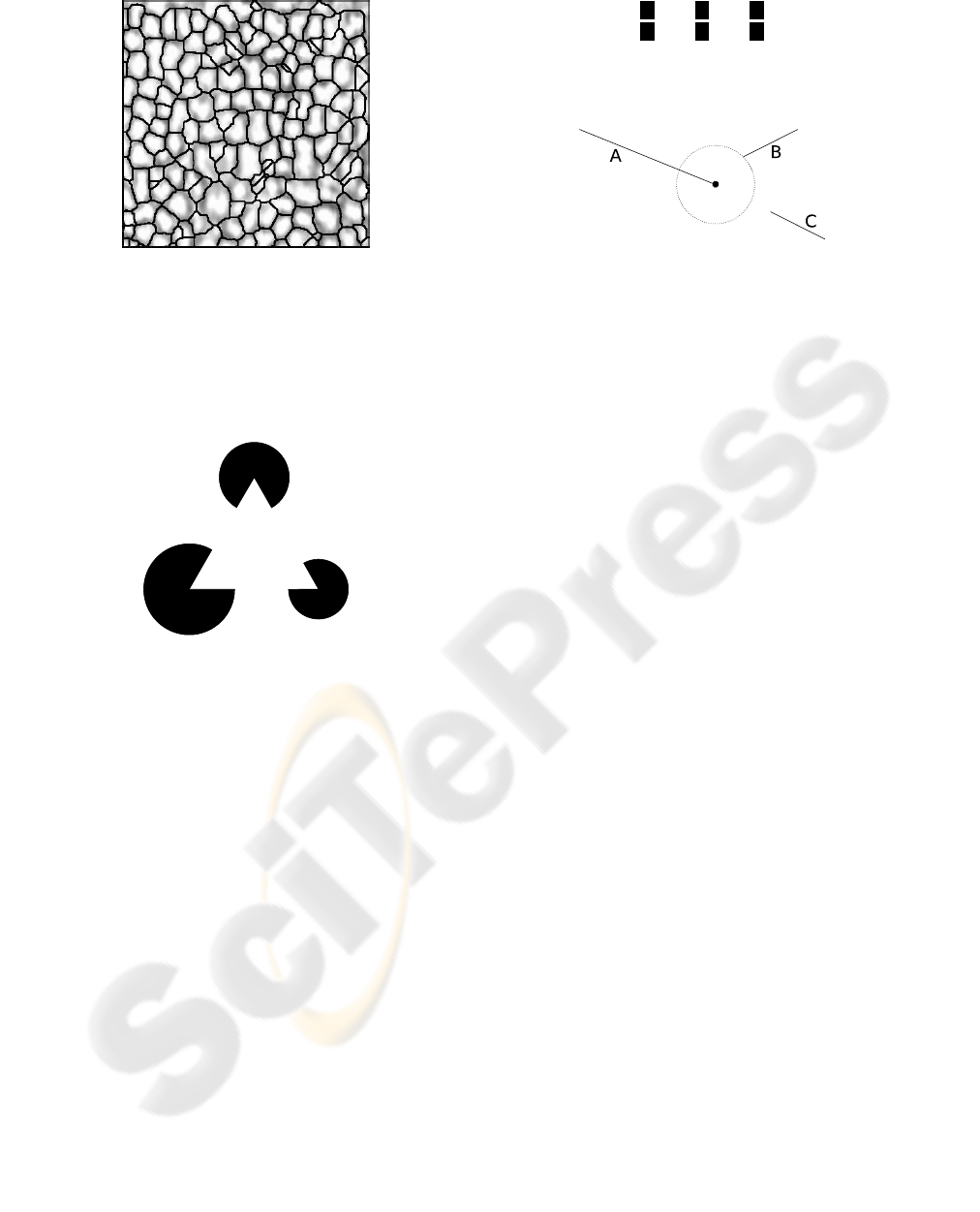
Figure 2: 400 × 400 pixels (0.4mm

) image of a hu-

man corneal endothelium acquired by standard optical mi-

croscopy. A software used by ophthalmologists has per-

formed a detection of contours in this image. The detected

cell map appears globally relevant, but some misdetection

can be clearly observed at several locations, (Debayle et al.,

2006).

Figure 3: A Kanizsa illusory triangle. Though not drawn,

the triangle is perfectly seen, or more precisely percepted.

But the fact is that the we see and infer informa-

tions, as illusory or subjective contours, that are not

really present in this image (Koffka, 1935) as for the

Kanisza triangle (Kanizsa, 1980) in the ﬁg. 3.

This is not because we are intelligent, it has been

proved that many animals could see illusory contours

(barn owls (Nieder, 2002), bees, etc.). Then, how

does the human visual system do to distinguish the

cells? Is there an efﬁcient method that could be im-

plemented in a computer to efﬁciently detect them?

The Gestalt Theory (Wertheimer, 1938) shows sim-

ple visual effects that mainly consist on grouping

some stimuli together according to certain principles

(proximity, good continuation, symmetry, etc.). Al-

though very attractive, they are not proved (they are

asserted by Wertheimer and the gestaltists as axioms),

but recent works show that these laws are biologically

or/and cognitively relevant (Kov´acs and Julesz, 1993;

Mullen et al., 2000). More, they appear really simple

and close to a mathematical or algorithm description,

but in fact, they are not. Those are reasons to develop

Figure 4: Grouping of elementary rectangles here is done

by proximity.

Figure 5: Each segment is grouped to the closest one

following the proximity principle. The circle shows the

Euclidean distance value from the extremity (marked point)

of the segment to the closest extremity. The segments A and

B are thus grouped by proximity.

computer programs to test the effects of the gestalt

principles.

2 ALGORITHMS: COMPUTER

VISION OF MOSAICS

This section introduces some gestalt principles (sub-

section 2.1) used on a real corneal endothelium (sub-

section 2.2). This conducts to deﬁne a mosaic as a

network of contours.

2.1 Implementing Gestalt Principles

The most basic objects used to described the gestalt

principles are points or curves. At ﬁrst sight, a curve

can be simpliﬁed as a set of segments and the follow-

ing algorithms use them as inputs to the gestalt prin-

ciples.

Proximity

Experiences done by (Kubovy and Gepshtein, 2000)

prove that proximity plays an important role in group-

ing objects together (ﬁg. 4 and 5).

Good Continuation

Good continuation (ﬁg. 6) is the visual effect noticed

when grouping is done with objects that shows a con-

tinuity of direction.

By using Gabor patches, (Dakin and Hess, 1999)

and (Mullen et al., 2000) prove that good continuation

(in an angular variation of 30

◦

) is important for the

vision: lines have not to be continuously drawn, even

if closed contours are visually more important than

Figure 6: The lines A-C and B-D are grouped by good con-

tinuation. Visually, we have to do an effort to see the groups

A-B and C-D.

Figure 7: The direction (cone C) of continuation is deﬁned

by the segment A and an angle of 30

◦

around the continuing

direction A’. If another extremity is inside the cone C, it

is considered as a weak continuation, as opposed to good

continuation (ﬁg. 8).

incomplete ones (Kov´acs and Julesz, 1993) (see ﬁg. 7

and 8).

Geodesic Proximity and Continuation

The distance transform is an operation that takes an

object and compute the Euclidean distance from this

object to any other point in the image (Rosenfeld and

Pfaltz, 1966): the result is the so-called distance map,

that can be represented as an image. The distance

transform is also used to compute the skeleton (Blum

and Nagel, 1978). The geodesic distance map is the

representation of the geodesic distance from the ob-

ject.

By using the Gestalt theory, the geodesic distance

map can be seen as a mix of proximity and continu-

Figure 8: The good continuation. is considered when the

weak continuity (ﬁg. 7) is effective for every extremity. C1

and C2 englobe respectively the extremities of B and A.

Figure 9: A simple mosaic. Holes are randomly performed

into it and the algorithm tries to close them.

ation. Each extremity of the contour is linked to the

nearest (by the geodesic distance) other extremity.

2.2 From the Corneal Endothelium

According to (Marr, 1983), the ﬁrst stage of percep-

tion consists in contour detection. This is the way

ophthalmologists analyze the cells in the corneal en-

dothelium.

The contours of the cells can be detected by using

mathematical morphology (Serra, 1988). Our algo-

rithm is inspired from (Chazallon and Pinoli, 1997).

With the skeleton of the borders of the cells (Blum

and Nagel, 1978), the goal is now to reconstruct the

cells with the principles described previously.

This type of image, e.g. the partition of the image

by planar objects, can be shown in different domains,

like materials (grains, dendrites), satellite imagery of

ﬁelds or cities, etc. This is why we now introduce an

abstraction of such a network we call a mosaic.

A 2D mosaic is a binary set of curves (we used

segments at ﬁrst approximation) (ﬁg. 9) in the Euclid-

ean plane space that can be the result of a contour de-

tection or a skeletonization of objects. For testing pur-

poses, we use a hand-drawn mosaic as the reference,

and perform holes on it: one part of the segments are

randomly erased to be then reconstructed (ﬁg. 9).

2.3 Results

Proximity and good continuation perfectly close the

theoretical mosaic (see ﬁg. 9), because they are really

adapted to the holes done into the it and to its segment

structure. About the real cornea (ﬁg. 10), proxim-

ity and good continuation show their limits: the algo-

rithm can link two extremities that are very far from

each other (and draws a segment that crosses the mo-

saic). The geodesic proximity can somehow be con-

sidered as a synthesis of proximity and continuation,

Figure 10: Application of the geodesic distance to recon-

struct the corneal endothelium. This method shows the lim-

its of a pure contour approach. The white pixels represent

the contours detected, and the black pixels represent the clo-

sure computed. The regional information is necessary to

ﬁnd a good closure.

but is not enough to give what was visually expected.

3 CONCLUSION

We decided to begin with simple principles of vision

and to implement them one by one. Those simple

principles reconstruct well simple mosaics. But real

mosaics like corneal endothelium are complex. The

conclusion of these tests is that when ophthalmolo-

gists count cells on the endothelium, a lot of visual

effects occur at the same time, not only proximity and

continuation (ﬁg. 10). To improve our methods, we

have combined proximity and continuation with a dis-

tance criteria (the geodesic continuation), and the re-

construction is not good yet.

As suggested by Marr, the human visual system

performs a Bottom-up-Top-down dual analysis; we

think that there is more than that: the human visual

system is sensitive to the duality region-contour and

unceasingly reinterpret the informations collected.

PERSPECTIVES

In a near future, we will use regional informations to

choose where to close the cells; and the proximity and

continuation methods will tell us how.

The perspectives for this work are to use regional

descriptors, size and shape parameters and contours

informations at the same time. We will also introduce

comparison methods between the mosaics to evaluate

the reconstruction, and test some other methods with

it. Those will be part of a PhD Thesis (Gavet, 2007).

REFERENCES

Blum, H. and Nagel, R. N. (1978). Shape description using

weighted symmetric axis features. Pattern Recogni-

tion, 10(3):167–180.

Chazallon, L. and Pinoli, J.-C. (1997). An automatic

morphological method for aluminium grain segmen-

tation in complex grey level images. Acta Stereol,

16(2):119–130.

Dakin, S. C. and Hess, R. F. (1999). Contour integration and

scale combination processes in visual edge detection.

Spatial Vision, 12:209–327.

Debayle, J., Gavet, Y., and Pinoli, J.-C. (2006). Image

analysis and recognition, chapter General Adaptive

Neighborhood Image Restoration, Enhancement and

Segmentation, pages 29–40. Lecture Notes in Com-

puter Science 4141. Springer Berlin / Heidelberg.

Gain, P., Thuret, G., Kodjikian, L., Gavet, Y., Turc, P. H.,

Theillere, C., Acquart, S., Petit, J. C. L., Maugery, J.,

and Campos, L. (2002). Automated tri-image analy-

sis of stored corneal endothelium. Br J Ophthalmol,

86(7):801–808.

Gavet, Y. (2007). Human vision principles and completion

of mosaics. application to human corneal endothe-

lium. PhD Thesis. To be published.

Kanizsa, G. (1980). Grammatica del vedere. Saggi su

percezione e Gestalt. Il Mulino, Bologna.

Koffka, K. (1935). Principles of Gestalt Psychology. Har-

court Brace.

Kov´acs, I. and Julesz, B. (1993). A Closed Curve is Much

More than an Incomplete One: Effect of Closure in

Figure-Ground Segmentation. PNAS, 90(16):7495–

7497.

Kubovy, M. and Gepshtein, S. (2000). Perceptual Orga-

nization for Artiﬁcial Vision Systems, chapter Gestalt:

from phenomena to laws, pages 41–71. Kluwers Aca-

demic Publishers.

Marr, D. (1983). Vision: A Computational Investigation

into the Human Representation and Processing of Vi-

sual Information. Henry Holt & Company.

Mullen, K. T., Beaudot, W. H. A., and McIlhagga, W. H.

(2000). Contour integration in color vision: a common

process for the blue-yellow, red-green and luminance

mechanisms? Vision Research, 40(6):639–655.

Nieder, A. (2002). Seeing more than meets the eye: process-

ing of illusory contours in animals. Journal of Com-

parative Physiology A: Sensory, Neural, and Behav-

ioral Physiology, 188(4):249–260.

Rosenfeld, A. and Pfaltz, J. L. (1966). Sequential operations

in digital picture processing. J. ACM, 13(4):471–494.

Serra, J. (1988). Image analysis and mathematical mor-

phology: Vol. 2. London: Academic Press.

Wertheimer, M. (1938). A sourcebook of Gestalt Psy-

chology, chapter Laws of Organization in Perceptual

Forms (partial translation), pages 71–88. Hartcourt,

Brace.