PRACTICAL SINGLE VIEW METROLOGY FOR CUBOIDS

Nick Pears, Paul Wright and Chris Bailey

Department of Computer Science, University of York, UK

Keywords:

Single View Metrology. 3D measurement. Feature detection. Planar homographys. Projective invariants.

Abstract:

Generally it is impossible to determine the size of an object from a single image due to the depth-scale ambi-

guity problem. However, with knowledge of the geometry of the scene and the existence of known reference

dimensions in the image, it is possible to infer the real world dimensions of objects with only a single im-

age. In this paper, we investigate different methods of automatically determining the dimensions of cuboids

(rectangular boxes) from a single image, using a novel reference target. In particular, two approaches will be

considered: the ﬁrst will use the cross-ratio projective invariant and the other will use the planar homography.

The accuracy of the measurements will be evaluated in the presence of noise in the feature points. The effects

of lens distortions on the accuracy of the measurements will be investigated. Automatic feature detection

techniques will also be considered.

1 INTRODUCTION

Historically, many package delivery companies have

priced the delivery of packages mainly by weight.

However, increasingly, tariffs are related to the size

of the package being delivered, as the cost of ship-

ping the package is more closely related to how much

space it takes up in the delivery chain. If there were

a simple and fast method to establish and log into the

company’s IT system the size of a package, then great

beneﬁts in terms of the whole system’s efﬁciency can

be achieved. We note that, already, package han-

dling staff often carry around mobile computer de-

vices called PDAs (personal digital assistants) to log

packages into the IT system and such devices are now

easily and readily equipped with cameras. This paper

aims to prove the principle that it is possible to mea-

sure the dimensions of a package from a single image

(for example, taken by a camera-equipped handheld

PDA), given a simple, portable reference target.

Measurement using images is termed visual

metrology and this has been studied extensively in

the computer vision literature (Criminisi et al., 1999),

(Criminisi, 2001), (Chen et al., 2006). In this paper,

we aim to automatically measure the dimensions of

cuboids (rectangular boxes) from a single image, us-

ing a simple, novel reference object attached to one

corner of the cuboid. The term automatically is used

here to mean that the only piece of information that

should be given to the system is the image of the scene

containing a box.

Several problems need to be addressed to build

such a measurement system. These include the re-

moval of distortions caused by the lens of the camera,

feature detection and identiﬁcation, and dimension

measurement. Each problem will need to be solved

to produce a system that can provide accurate, auto-

matic measurements.

This paper will look at two particular methods to

compute the dimensions of a box: the cross-ratio in-

variant and the planar homography. For this type of

measuring system to be of practical use, as is the case

with all measuring systems, the results it returns have

to be accurate and reliable. It is therefore important to

assess the reliability of both techniques being investi-

gated.

The remainder of the paper is structured as fol-

lows. In section 2, we describe the two measurement

techniques, which we aim to compare. In section 3,

we describe the implementation of our measurement

system. In section 4, we present results of both sim-

ulations and real measurements and a ﬁnal section is

used for conclusions.

Pears N., Wright P. and Bailey C. (2007).

PRACTICAL SINGLE VIEW METROLOGY FOR CUBOIDS.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 85-90

 SciTePress

Figure 1: Cross ratio based measurement.

2 MEASUREMENT TECHNIQUES

The reference target used consists of three mutually

orthogonal, equally sized square faces, coloured with

a 2x2 chessboard pattern on each face, as shown in

ﬁg 1. The size of the squares within the pattern are

40mm. Our target is constructed of cardboard, but

in a practical PDA-based system, we envisage that a

rugged and foldable plastic target may be used.

The colours within the reference target were care-

fully selected, so that adjacent squares in the pat-

tern have high contrast in greyscale, which allows,

for example, reliable corner detection. Target cor-

ners are identiﬁed from their normalised colour his-

tograms within a local circular neighbourhood. If all

the corners in the target are detected, this gives rise

to nine points on each target plane and three points

along each axis.

2.1 Metrology Using Invariants

Figure 1 shows an image of a box to be measured,

with the reference target in-situ. The reference points

that need to be detected in the image are shown

by white dots along three mutually orthogonal axes.

These image points are labelled (a

− d

), as shown,

where i is the one of the dimensions (x, y, z).

If we represent world coordinates as

, B

, D

), corresponding to image points

, b

, c

, d

) along dimension i, then we can write an

equation for the invariance of the cross-ratio under

the imaging process. Using the notation d(., .) to

represent the Euclidean distance between a pair of

points, then (Hartley and Zisserman, 2000)

d(a

, c

)d(b

, d

)

d(b

, c

)d(a

, d

)

d(A

)d(B

, D

)

d(B

)d(A

, D

)

(1)

If one of the four squares on a target face has di-

mension α, then

2α(M

− α)

αM

(2)

Figure 2: Homography based measurement.

where I

is the invariant computed from image mea-

surements along the i dimension and M

is the un-

known measurement of the box in the i dimension,

expressed in the same units as α (typically we use

millimetres). Rearranging this equation, we have

(1− 0.5I

)

(3)

2.2 Metrology Using Homographys

The second method of calculating the box dimensions

uses the planar homography approach, and in par-

ticular, the normalised Direct Linear Transformation

method is used (Hartley and Zisserman, 2000).

In contrast to the cross ratio invariant, which uses

three edges of the box, the planar homography instead

uses planes of the box. Since each plane is bounded

by two axes of the box, each plane can provide a max-

imum of two dimensions of the box. Therefore a min-

imum of two planes need to be visible in order to cal-

culate all three dimensions of the box from a single

image as shown in Figure 2.

Since two planes are required for all three dimen-

sions of the box to be recovered, this means that two

homographies will need to be calculated, due to each

plane of the box undergoing a different projective

transformation during the imaging process.

The relative world position of the reference tar-

get corners are known, and through feature detection,

their corresponding image positions can be extracted

from the image. This means that the target can pro-

vide nine point correspondences per plane - more than

the minimum of four (no three collinear) required to

calculate a planar homography.

Once the homographies have been calculated, the

real world position of any point on either plane of the

box can be determined. Since the external corners of

the box lie on these planes, their real world position

can be determined through the homography. The cor-

ner relating to the height exists on both planes, so ei-

ther plane can be used to calculate this dimension, or

alternatively, an average taken.

Figure 3: Feature points required for the cross ratio.

3 IMPLEMENTATION

Our system is implemented in MATLAB with the fol-

lowing the main stages:

(i) Image acquistion: A Kodak LS743 digital cam-

era was used to collect images, using the wide angle

lens setting. After capture, images are reduced from

2304 x 1728 down to 800 x 600 to reduce image pro-

cessing time.

(ii) Camera Distortion Correction: The MATLAB

Camera Calibration Toolkit (Bouguet, 2005) was used

to correct the radial distortions in the input images.

Our calibration results showed that radial distortion

has the greatest effect towards the corners of the im-

age where there are displacements of up to 50 pixels.

The effects of tangential distortions are much smaller

with only a maximum displacement of 2 pixels. With

the camera intrinsics calculated, any image can then

be corrected by the toolkit.

(iii) Corner Detection: The implementation of the

Harris corner detector (Harris and Stephens, 1988) by

Peter Kovesi (Kovesi, 2000) was used. Other interest

point detectors could also be used such as the SUSAN

detector (Smith and Brady, 1995).

(iv) Feature Point Recognition: Figure 3 illus-

trates the points required to calculate the cross ratios.

The ﬁrst feature we try to identify is the central

point of the reference target, using the surrounding

colours. Colour modelling is an area that has been

researched extensively in computer vision (Alexan-

der, 1999). The approach used here is similar to that

used by Coughlan et al (Coughlan et al., 2005). For

each candidate corner, three points p

, p

and p

are

speciﬁed at ﬁxed offsets, separated by 120 degrees,

such that each point is positioned in a region of red,

green or blue colour. If the letters R

, G

and B

rep-

resent the red, green and blue intensity values at point

, then the colour target is detected if the following

four inequalities are met: R

> R

+T, G

+T < G

> G

+ T, R

> R

+ T, where T is a threshold

value used to control the detection. It should be noted

that use of this technique does require the reference

target to be placed on the box in a speciﬁc way such

that the red region is always at the top. This approach

produces accurate and reliable detection of the target.

Once the centre of the reference target has been iden-

tiﬁed, the next step is to search for the surrounding

three points of the target that sit on the axes of the

box. These can be used to determine the direction of

the three axes of the box. These points are found in

a similar way to ﬁnding the centre of the reference

target, although different colour regions need to be

speciﬁed for each of the points.

Along each axis, the location of two points is now

known, so an approximate direction of each axis can

be calculated. The placement of the reference target

on the corner of the box is unlikely to be perfect due to

deformations of the box. Thus a search region along

each axis is determined in which to ﬁnd the other re-

quired points. This search region narrows down the

number of corners that will have to be investigated.

The third point on the reference target can now be lo-

cated, again using the colour region method.

The external corner of the box is found by

analysing the colour in the region next to each corner

detected in the search region. It is assumed that close

to the edge of a box, the colour and texture of the box

should remain roughly the same. It is also assumed

that the box colour should be markedly different to

that of its background. The image is ﬁrst converted

from RGB space to HSI space. A histogram of the

hue for a small region next to the ﬁnal point detected

on the reference target is then obtained.

For each corner detected in the search region, a

histogram for the surrounding region is obtained. This

corner histogram is then compared to the histogram of

the region next to the target previously stored. If the

two histograms are different by some margin, then the

detected corner is likely to be a corner of the box.

(v) Metrology Calculations: The cross ratio

method was straightforward to implement. From the

set of image point coordinates, the distances between

them were calculated and the values put into equation

3 to obtain each dimension of the box. The planar

homography method used the normalised DLT algo-

rithm to estimate a homography matrix for each plane.

Then the image coordinates of the box corners were

converted into the real world coordinates, which was

used to compute the length of a side of a box. Both

planes can be used to obtain the height measurement

of the box, so the average of the two values obtained

from both planes is used as the height measurement.

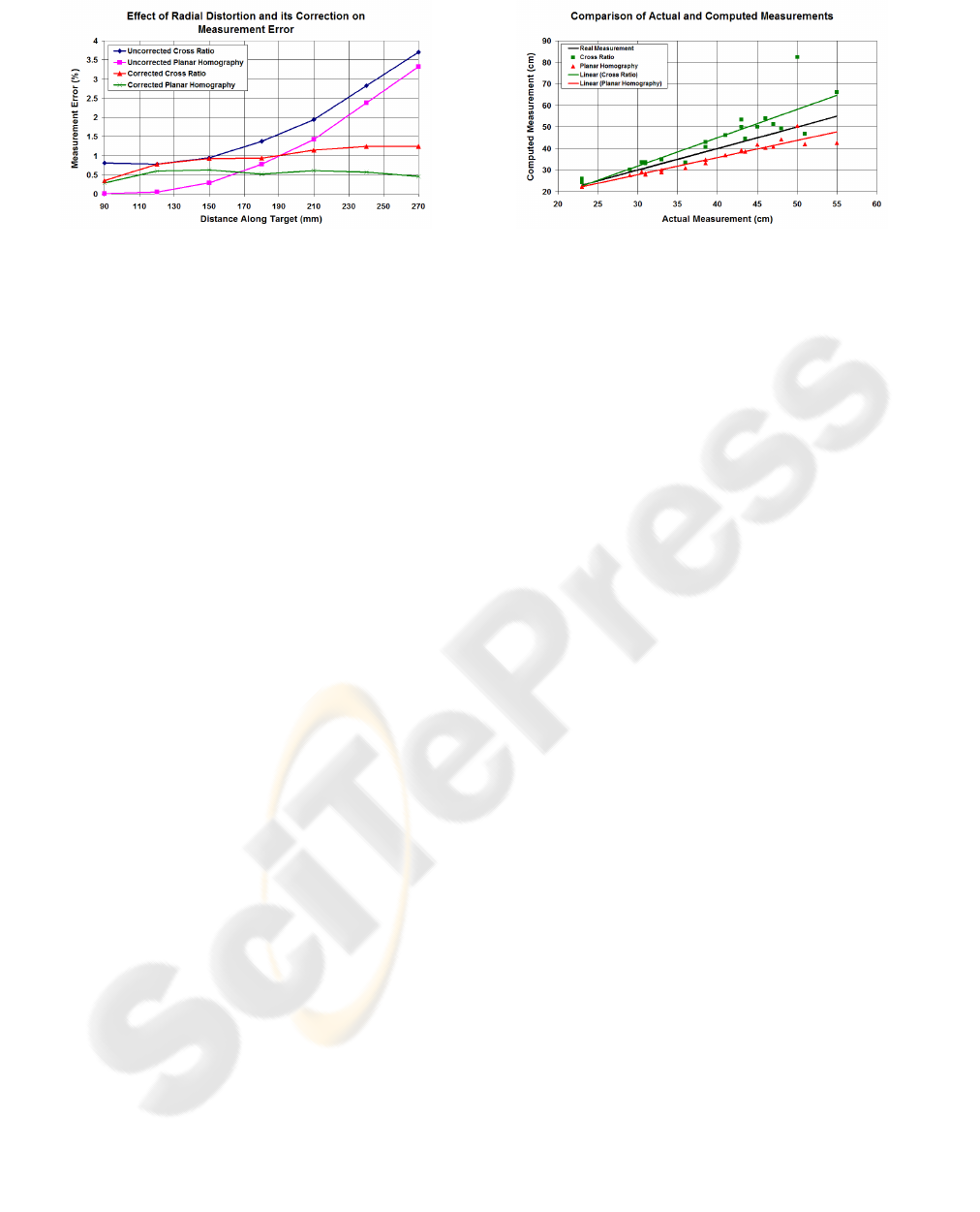
Figure 4: Th effect of radial distortion.

4 RESULTS AND EVALUATION

4.1 Radial Distortion Correction

To what extent does radial distortion affect the mea-

surements and do the correction techniques employed

reduce these errors? To answer these questions, a

marked calibration plane was set up in front of the

camera so that it almost entirely ﬁlled the captured

image. The image was then corrected for radial dis-

tortion and both the uncorrected and corrected im-

ages were stored. The position in the image of each

30 mm graduation along both the x and y axes was

selected by eye. Each 30 mm graduation is consid-

ered to be the box corner, allowing the trend in mea-

surement error across the image to be observed. For

each graduation mark in both the uncorrected and cor-

rected image, its estimated position was calculated

and stored using both the cross ratio and planar ho-

mography methods.

The error in the measurements for both methods in

both the uncorrected and corrected images are shown

in Figure 4. Both the results in the x and y axis of the

plane were very similar, so Figure 4 only shows the

results obtained from the x axis. From this graph it is

clearly visible that radial distortion has a noticeable

effect on the accuracy of the results obtained from

both methods. For the uncorrected cases, the errors

start low, but increase rapidly to as much as 3.75%.

Note, however, that the radial distortion correction

signiﬁcantly improves the accuracy of the results and,

for both the planar homography and cross ratio tech-

niques, the measurement errors stay relatively con-

stant across the entire calibration grid.

4.2 Comparison of Methods

Twenty two boxes were selected, ensuring a mixture

of small and large boxes and boxes with different as-

pect ratios. Images of each were captured from three

Figure 5: Comparison of actual and computed measure-

ments for 22 boxes in view 1.

views, the ﬁrst of which (view 1) was such that the

camera was pointing directly through the diagonal of

the box. Each captured image was corrected for radial

distortion and feature points on the reference target

and the box corners were selected. The dimensions

of the box were then obtained from both the cross ra-

tio and planar homography methods. Firstly, the ac-

curacy of both methods will be compared. Figure 5

shows the difference between the real measurement

and the measurements estimated by both techniques

for just the width of the box. The central diagonal

(black) line shows the ideal situation where the vi-

sual metrology is perfect and there are no errors in

the measurements. The points with square markers

(green) show the measurements made using the cross

ratio for each of the 22 boxes. The points with tri-

angular markers (red) show the measurements made

using the planar homography technique. Linear least

squares trend lines for both sets of measurements are

shown.

Note that the measurements obtained are in gen-

eral close to the correct value, although they suffer

from both systematic and random error. In many ways

it is unreasonable to expect highly accurate answers,

since it can be difﬁcult to position the reference target

on the box so that it lies ﬂat on the plane. This is due

to the fact that the boxes are not perfectly cuboid and

the corners can be deformed. Interestingly, the sys-

tematic errors show a deﬁnite trend for the cross ratio

to overestimate the measurement whereas the planar

homography underestimates, although both of these

effects can be calibrated out, such that the trend lines

for both methods are coincident with the true mea-

surements.

From the graph, the repeatability of the measure-

ments made by both the cross ratio and planar ho-

mography methods can be compared. This can be

achieved by looking at the spread of points from their

trend line. The planar homography method produces

more stable estimations since the points are situated

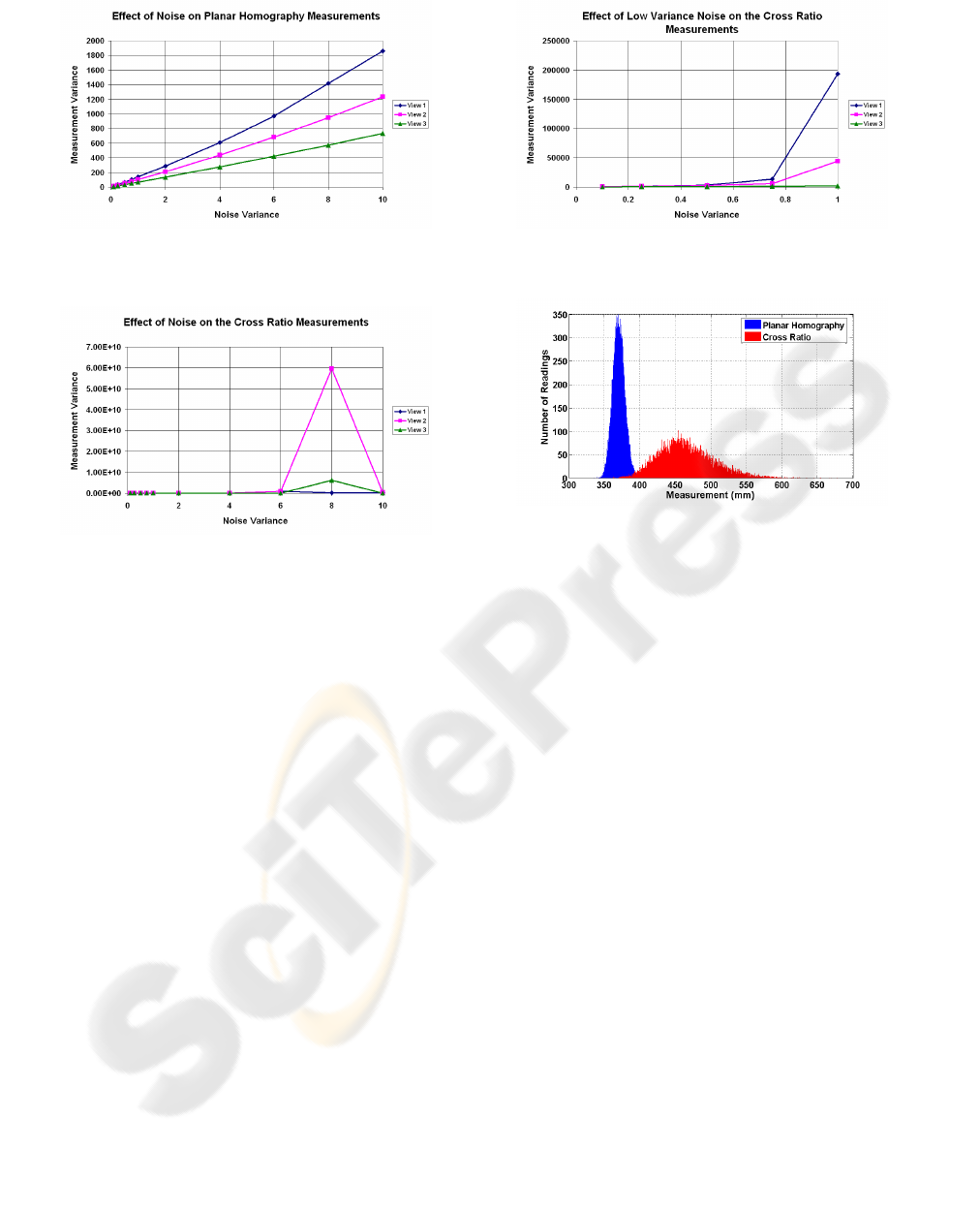
Figure 6: Effect of noise on planar homography measure-

ments.

Figure 7: Effect of noise on cross ratio measurements.

closer to its trend line. However, for the cross ratio

method, the points are often situated further from the

trend line, with their distance increasing further from

the trend line as the size of the box increases and the

relative size of the imaged reference target decreases.

4.3 Noise Sensitivity

Within the context of this work, noise will be de-

ﬁned as movements of the detected feature points

from their expected (ideal) positions. A noise sensi-

tivity experiment was conducted as follows. For each

of the 22 undistorted test box images, the points of

the reference target and the box corners were sub-

jected to Gaussian noise with a certain variance. The

dimensions of the box were then calculated using

both the cross ratio and the planar homography tech-

niques. These measurements were stored and the fea-

ture points subjected to a new set of noise. This was

repeated 10,000 times, so 20,000 measurements were

recorded in total. This whole procedure was then re-

peated for noise variances of 0.1, 0.25, 0.5, 0.75, 1,

2, 4, 6, 8 and 10. (Note that only the width measure-

ment is used in this experiment.) For each set of mea-

surements, a series of statistics were generated such

as the average, variance and standard deviation. In

the following ﬁgures the noise variance is in (pixel

Figure 8: Effect of low variance noise on the cross ratio

measurements.

Figure 9: Histogram comparing effect of noise on the two

methods.

position)

and the measurement variance is in (mm)

The effects of noise on the planar homography

method will ﬁrst be considered. Figure 6 shows the

variance of the width measurement as a function of

noise variance. We note that, although the planar ho-

mography is deﬁnitely susceptible to the effects of

noise, its effects are predictable. The difference in the

curves for the three views can be attributed to the fact

that going from view one (camera pointing along box

diagonal) to view 2 (camera pointing at front edge, no

top plane, width and depth have equal image size) to

view three (as view 2, but width has larger image size

than depth) favours more accurate measuring of the

width of the box.

Figure 7 shows the effects of noise on the cross ra-

tio method. Here the noise presents a much more seri-

ous problem. Not only is the variance in the measure-

ments much greater now than for the planar homog-

raphy, the relationship between the amount of noise

and measurement variance is signiﬁcantly more non-

linear. This is seen clearly in Figure 8 which shows

the effects of low variance noise only.

Another way in which the data from this exper-

iment can be analysed is using a histogram to show

the spread of the results obtained from both methods.

Figure 9 shows the histogram of the results obtained

from the width measurement of a particular box. The

mean position of the two histograms is different due

to the difference in the systematic error of the under-

lying measurement made by both techniques (see Fig-

ure 5). However, this graph shows a clear difference

in the repeatability of the two methods in the presence

of noise. Whereas the planar homography histogram

is tall and narrow, the cross ratio histogram is short

and wide. This indicates that planar homography is

less sensitive to noise that the cross ratio method.

5 CONCLUSIONS

We have presented a novel reference target method for

the measurement of cuboid (box) dimensions, with a

view to producing a PDA-based system in the near

future. Using corner features on this target, we have

outlined two methods that can be used to measure box

dimensions from a single image: the cross ratio in-

variant and planar homography. Accuracies of around

5.3% show that, although our prototype is not highly

precise, it has sufﬁcient accuracy for logging approx-

imate parcel dimensions in a parcel delivery IT sys-

tem, which can greatly improve resource planning in

the delivery chain. We conclude by answering ﬁve

important questions.

1. How accurately can box measurements be made?

For view 2, average errors of 6.7% for the

cross-ratio method and 5.3% for the homography

method were measured. This is a reasonable level

of accuracy to expect considering that it is difﬁ-

cult to align the reference target on the corner of a

possibly non-cuboid box. Furthermore, accuracy

may be improved by calibrating out systematic er-

rors in each method.

2. Can the required features of a box be detected reli-

ably? We have not fully answered the question of

whether completely automatic measurements can

be made. It is accepted that the feature detection

methods used in this project are basic in compari-

son to others available, which, could for example

involve SIFT features (Lowe, 2004) and pay more

attention to colour modelling (Alexander, 1999).

However, for the cross ratio method it has been

shown that it is possible to detect the required fea-

ture points automatically, although this is only re-

liable on plain boxes (no patterns or text).

3. What are the ideal conditions for measurements?

For the most accurate measuring, the three lines

required for the cross ratio or the two planes re-

quired for the planar homography should occupy

as large an area of the image as possible.

4. How are the measurements altered in the presence

of noise in the input? The measurements made by

both the cross ratio and the planar homography

methods have been investigated when the posi-

tions of the feature points are subject to noise. We

found that the cross ratio method is much more

sensitive to the effects of noise than the planar ho-

mography method.

5. Do the effects of camera distortion affect the ac-

curacy of the measurements and can the effects of

the distortions be corrected or minimised? The

problems of radial distortion have been investi-

gated and it has been shown that this form of dis-

tortion has an effect on the accuracy of the mea-

surements. Radial distortion can be corrected and

performing this operation removes signiﬁcant in-

accuracy in the measurements (as much as 3% er-

ror). It is therefore imperative that radial distor-

tion is corrected before a measurement is made

from the image.

REFERENCES

Alexander, D. (1999). Advances in daylight statistical

colour modelling. In Proc. Conf. Computer Vision and

Pattern Recognition, pages 313–318.

Bouguet, J. (2005). Camera calibra-

tion toolbox for matlab 2005. url:

http://www.vision.caltech.edu/bouguetj/calib-doc/.

Chen, Z., Pears, N. E., and Liang, B. (2006). A method of

visual metrology from uncalibrated images. Pattern

Recognition Letters, 27(13):1447–1456.

Coughlan, J., Manduchi, R., Mutsuzaki, M., and Shen, H.

(2005). Rapid and robust algorithms for detecting

colour targets. In Proc. 10th Congress of the Inter-

national Colour Association.

Criminisi, A. (2001). Accurate visual metrology from single

and multiple uncalibrated images. Springer.

Criminisi, A., Reid, I., and Zisserman, A. (1999). Single

view metrology. In Proc. 7th Int. Conf. on Computer

Vision, pages 434–442.

Harris, C. J. and Stephens, M. (1988). A combined cor-

ner and edge detector. In 4th Alvey Vision Conference

Manchester, pages 147–151.

Hartley, R. I. and Zisserman, A. (2000). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press.

Kovesi, P. D. (2000). Matlab and octave functions

for computer vision and image processing. url:

http://www.csse.uwa.edu.au/ pk/research/matlabfns/.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 2(60):91–110.

Smith, S. M. and Brady, J. M. (1995). Susan-a new ap-

proach to low-level image processing. Int. Journal of

Computer Vision, 23(1):45–78.