AUTOMATED SEPARATION OF REFLECTIONS FROM A SINGLE

IMAGE BASED ON EDGE CLASSIFICATION

Kenji Hara, Kohei Inoue and Kiichi Urahama

Department of Visual Communication Design, Kyushu University, Fukuoka, Japan

Keywords:

Reﬂection separation, transparency, edge classiﬁcation, pyramid structure, deterministic annealing.

Abstract:

Looking through a window, the object behind the window is often disturbed by a reﬂection of another object.

In the paper, we present a new method for separating reﬂections from a single image. Most existing techniques

require the programmer to create an image database or require the user to manually provide the position and

layer information of feature points in the input image, and thus suffer from being extremely laborious. Our

method is realized by classifying edges in the input image based on the belonging layer and formalizing the

problem of decomposing the single image into two layer images as an optimization problem easier to solve

based on this classiﬁcation, and then solving this optimization with a pyramid structure and deterministic

annealing. As a result, we are able to accomplish almost fully automated separation of reﬂections from a

single image.

1 INTRODUCTION

One can see that the scene observed through a ﬂat

transparent plate such as window glass normally con-

sists of a combination of two images: the reﬂected

image and the transmitted image. In recent years, de-

composing the superimposed image into the two im-

ages has been a topic of signiﬁcant interest in the com-

puter vision community because of both its practical

importance and its theoretical difﬁculty.

The great difﬁculty of the image decomposition

problem lies in its high illposedness, since the num-

ber of unknowns (twice the number of pixels) is much

larger than the number of available constraints (the

number of pixels) (Levin et al., 2004a). Thus, much

of the image decomposition methods enforce addi-

tional constraints such as using as inputs two im-

ages taken through a polarizer at different orienta-

tions or using an image sequence taken from a video

camera (Farid and Adelson, 1999; Irani and Peleg,

1992; Sarel and Irani, 2004b; Sarel and Irani, 2004a;

Szeliski et al., 2000; Tsin et al., 2003; Schechner

et al., 2000)D

More recently, Levin et al. (Levin et al., 2004a)

developed a method for decomposing the input image

into two images from a single image. This method is

based on a prior that prefers decompositions that min-

imize a linear combination of the numbers of edges

and corners. In this work, they showed that the sin-

gle image decomposition problem can be solved even

without a priori knowledge about content or scene

contents. Also at the same period, they proposed a

user-guided semi-automatic method, which work well

even on complex images that may be difﬁcult for the

above method to decompose (Levin et al., 2004b).

These previous works, however, require the pro-

grammer to create a database of natural images or re-

quire the user to manually provide the position and

layer information of feature points in the input image.

Hence, they suffer from the problems that the manual

data entry tasks are extremely laborious and tedious

and that the separation results may depend on the set

of images in the database.

In this paper, we present a single image decom-

position method that requires less labor, such as im-

age database construction or a considerable amount

of user interaction. In order to reduce the ambiguity

of the solution, we make the following assumptions

within Levin et al’s prior framework: (1) both of the

layers have edges, (2) the edge of a layer does not

Hara K., Inoue K. and Urahama K. (2007).

AUTOMATED SEPARATION OF REFLECTIONS FROM A SINGLE IMAGE BASED ON EDGE CLASSIFICATION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 18-25

 SciTePress

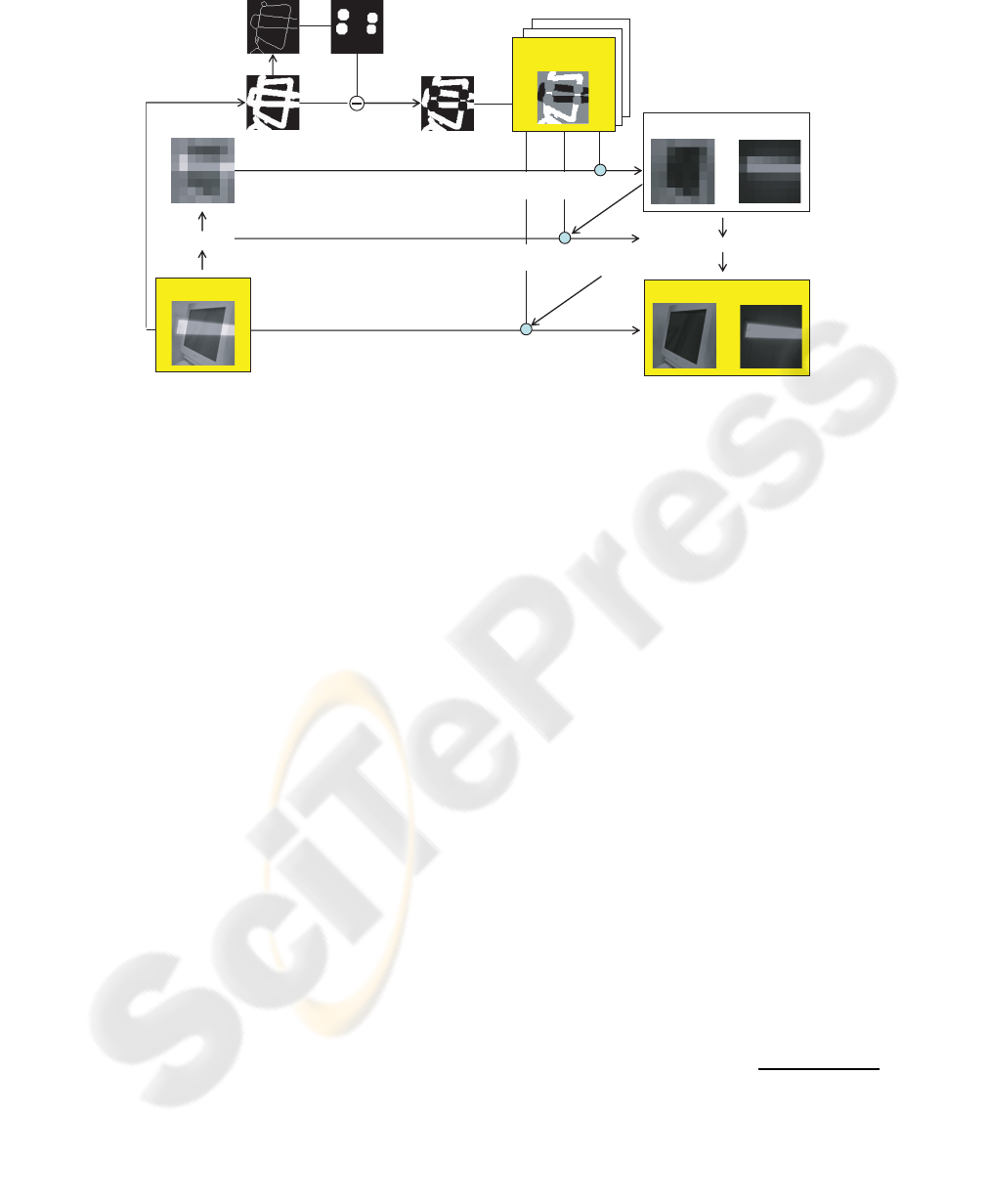
(8) low resolution layers

(1) input image

(6) classified edges

(2) edges

(3) thinned edges

(4) crossing edges

(5) edges belonging

to either layer

(7) low resolution image

(9) original resolution layers

decomposition

Figure 1: Pipeline of reﬂection separation.

overlap with any edge of another layer, and (3) the

junction edge in the superposition image arises from

the crossing between an edge of a layer and an edge

of another layer.

We ﬁrst identify each edge pixel in the input im-

age to which layer it belongs using only low level

image features. We then formulate the problem of

decomposing the single image into two layer images

as an optimization problem easier to solve based on

this classiﬁcation. We show that this optimization

can be approximately solved using a pyramid struc-

ture and deterministic annealing (Geiger and Girosi,

1991; Urahama and Nagao, 1995; Ueda and Nakano,

1998).

2 PROBLEM FORMULATION

Recently, Levin et al. proposed an optimization

frameworkfor separating reﬂections from a single im-

age (Levin et al., 2004a). They formulated the prob-

lem of decomposing the single superimposed image

I = [I(x, y)] ∈ R

into two layers I

= [I

(x, y)] ∈ R

and I

= [I

(x, y)] = [I(x, y) − I

(x, y)] ∈ R

, where

D is the input image domain, as minimizing the cost

function:

cost

, I

) = cost

) + cost

), (1)

where cost

) is the total amount of edges and cor-

ners of I

cost

) =

∑

(x, y)∈D

|∇I

(x, y)|

+ ηc(x, y;I

)

, (2)

where ∇ is the gradient edge operator and c(·) is the

Harris-like corner operator. Also, α, β, and η are set

to 0.7, 0.25, and 15, respectively, which are obtained

from the histgrams of the operators in natural im-

ages (Levin et al., 2002). They provided solutions for

the problem by dividing the image into overlapping

patches and then selecting the optimal set of patches

from a database of natural image patches.

In the approach mentioned above, the problem of

separating reﬂections using a single image without

such training data or user intervention have not been

tackled. In this section, to address this difﬁculty, we

will provide an optimization framework.

2.1 Automatic Classiﬁcation of Edges

In our work, we ﬁrst estimate to which layer each

edge pixel in the input superimposed image belongs

according to the following procedure.

1. Detect edges

We detect edges in the input image with the SU-

SAN edge detector (Smith and Brady, 1997) (see

also Figure 1 (1))

n(x

, y

; I, t) =

∑

(x,y)∈D

c(x, y, x

, y

; I, t) , (3)

c(x, y, x

, y

; I, t) = 1− exp



−



I(x, y) − I(x

, y

)





(4)

where I(x

, y

) is the intensity value at the pixel

position (x

, y

) of the input image I and t is the

edge difference threshold parameter. We hereafter

denote by E the set of edge pixels.

2. Extract edges belonging to either layer

We obtain the set of connected regions, C =

|1 ≤ i ≤ m}, by ﬁrst reducing edges to unit

thickness while maintaining its topology (Fig-

ure 1(2)) and then performing morphological di-

lation of each pixel lying on the intersection of

the two lines with a circular structuring element

of appropriate size (Figure 1(3)). A region which

is C subtracted from the region E can be regarded

as belonging to either layer and can be segmented

into regions ω = {ω

|1 ≤ j ≤ n}, where each ω

is a connected region and ω

∩ ω

= φ for j 6= k

and n is the number of ω

(Figure 1(4) and Fig-

ure 2(a)).

3. Identify for each edge to which layer it belongs

While tracking around the pixels in the outer

boundary of each C

, we sequentially assign a la-

bel to each pixel indicating to which ω

it belongs

(no label is assigned to the pixel belonging to none

of ω

) (Figure 2(b)). In this process, four kinds of

labels j

, j

will appear (Figure 2(c)). Then,

we can impose the constraint that two regions ω

and ω

(also, ω

and ω

) belong to the same

layer. Hence, we can classify each edge region to

which layer it belongs by solving a set of the con-

straints for all C

∈ C (Figure 1(5)). We denote by

Ω

, Ω

, and Ω

the edge region of the ﬁrst layer,

the edge region of the second layer, and the other

region, respectively (Figure 2(d)).

2.2 Deﬁnition of Objective Function

We formulate the problem of separating reﬂections

from a single image. To make the presentation easy

to read without loss of generality, we will describe

and I

as I

= [I

(x, y)] = [α(x, y)I(x, y)] ∈ R

and

= [I

(x, y)] = [(1 − α(x, y))I(x, y)] ∈ R

, respec-

tively, by introducing the set of unknown coefﬁcients,

α = [α(x, y)] ∈ [0, 1]

. Then, the task of separating

two transparent layers becomes solving the minimiza-

tion problem as follows.

min

f(α; I, t) ≡ min

∑

(x, y)∈D

(x, y)n(x, y; α∗ I, t)

(x, y)n(x, y; (E − α) ∗ I, t), (5)

where α ∗ I = [α(x, y)I(x, y)] ∈ R

, (E − α) ∗ I =

[(1− α(x, y))I(x, y)] ∈ R

, n(x, y; I, t) is the function

deﬁned by Equation (4), w

= [w

(x, y)] ∈ R

and

= [w

(x, y)] ∈ R

are the variable weighting func-

tions as

(x, y) =







normal

(x, y) ∈ Ω

small

(x, y) ∈ Ω

large

(x, y) ∈ Ω

(6)

(b)

(c)

(d)

(a)

Figure 2: Classifying each edge according to the layer it

belongs to.

(x, y) =







normal

(x, y) ∈ Ω

large

(x, y) ∈ Ω

small

(x, y) ∈ Ω

(7)

where w

normal

= 1.0, w

large

= 10.0Cw

small

= 0.1. For

a relatively small region of Ω

∪ Ω

(for a relatively

large region of Ω

), the cost function in Equation (5)

becomes multimodal and there are local minima.

2.3 Heuristic Minimization

Next, we consider to employ a simple local search

strategy with a steepest descent heuristic to solve

the nonlinear problem of solving Equation (5). This

consists of setting the initial state of α, select-

ing a pixel with coordinates (x, y) at random, and

then replacing the value of α(x, y) at the current

time step by the neighboring solution that minimizes

Equation (5) within the neighborhood {α(x, y) −

δ, α(x, y), α(x, y) + δ} ; if a solution with no improv-

ing neighbor has been reached, the above heuristic

stops, and otherwise it is iterated.

Although the objective function in Equation (5)

appears to be easier to minimize than the objective

function in Equation (1), Equation (5) also still has

high multimodality and high dimensionality, and thus

the above local search often leads to local minima in

the search space. Examples of the results obtained

using this approach are shown in Figure 3 on a very

simple synthetic image. Figure 3(a) and Figure 3(b)

show the input superimposed image and the ground

truth layers, respectively. Figure 3(c) shows the re-

sult obtained using the local search described in this

section. Figure 3(d) shows another result where the

edge classiﬁcation described in Section 2.1 was not

utilized. These results show that even though the edge

classiﬁcation can improve the performance, this com-

plex nonlinear optimization problem in Equation (5)

cannot be solved in any way directly using the sim-

ple heuristic described above. To solve Equation (5),

we can apply powerful deterministic annealing tech-

niques as we will see in the next section.

3 IMAGE DECOMPOSITION

The output of the SUSAN edge detector ranges from

0 (non-edge) to 1 (edge). In Figure 4, each horizon-

tal bar in the graph represents the values of the SU-

SAN edge detector, n(x, y; I, t), for a ﬁxed t, with re-

spect to variation of the gradient magnitude of pixel

at position (x, y). One can see that large t makes the

SUSAN edge detector less sensitive and thus makes

n(x, y; α∗ I, t) and n(x, y; (E − α) ∗ I, t ) in Equation

(5) more uniform over the xy-plane. Also, the lower

the space frequency of the input image I is, the more

uniform n(x, y; α∗ I, t) and n(x, y; (E − α) ∗ I, t ) will

become. In this way, the number of local minima

of the objective function (5) decreases monotonically

with increasing t and smoothed image I.

Based on the above observation, in our frame-

work, we solve Equation (5) using a pyramid struc-

ture and deterministic annealing (Geiger and Girosi,

1991; Urahama and Nagao, 1995; Ueda and Nakano,

1998). After building a multiresolution image pyra-

mid from the input image, we start decomposing the

low resolution image into two images. Until the high-

est resolution (original image), the solution is prop-

agated to the next higher resolution where it is used

as the initial estimate. At each resolution level, the

deterministic annealing is performed by initially set-

ting t to a sufﬁcient large value and then gradually de-

(a) (b)

(e) (f)

Figure 3: Importance of edge classiﬁcation and annealing.

(a) Input image. (b) Ground truth images. (c) Without edge

classiﬁcation and without annealing. (d) With edge classi-

ﬁcation and without annealing. (e) Without edge classiﬁ-

cation and with annealing. (f) With edge classiﬁcation and

with annealing.

creasing it after each iteration, as shown in Figure 5.

The whole procedure of our algorithm is described in

detail below.

1. Extract edges from the input image (I) and clas-

sify each edge to which layer it belongs (Sec-

tion 2.1).

2. Build a pyramid representation of the input image.

In this case, the multiresolution image pyramid

has multiple layers with the original image at the

bottom and compressed (lower spatial resolution)

images at the upper layers. A layer pixel has the

value averaged over the corresponding next lower

(higher spatial resolution) layer four pixels. In this

paper, we choose the number of pyramid layers as

3. Set the current layer to the top most layer and

initialize the separation coefﬁcients (α) such that

α(x, y) = 0.5 for all (x, y) ∈ D.

4. Decompose the current layer image into two im-

ages. In this case, if the current layer is the top

most layer, the initial values of α are set as spec-

iﬁed above, otherwise are set such that the esti-

mated value of α(x, y) of the next upper layer is

mapped to the corresponding four pixels of the

current layer, for all (x, y). Then, decompose the

current layer image according to the following an-

nealing procedure (steps (a) to (c)).

Figure 4: Edge detection sensibility with respect to varia-

tions of t. The horizontal and vertical axes represent the

gradient magnitude and t, respectively.

resolution

large

small

low

high

Figure 5: Reﬂection separation with a pyramid structure and

deterministic annealing.

(a) Initially set the edge difference threshold para-

meter (t) of the SUSAN edge detector to a large

value.

(b) Compute α under the current layer and t value

using the heuristic minimization (Section 2.3).

(b) until t reaches its destination.

5. Iterate between moving to the next lower layer

and ﬁnding the best composition under this layer

(step. 4) until the bottom layer (the original im-

age) is reached.

6. If multiple edge classiﬁcations are possible

(Section 2.1), perform the image decomposition

(steps 1 to 5) for each classiﬁcation and then

select the decomposition result which solves

Equation (5) in the case where Ω

∪ Ω

= φ,

i.e., w

(x, y) = w

normal

for all pixel

(x, y) ∈ D.

Figures 3(e), (f) show the decomposition results

obtained using deterministic annealing with and with-

out edge classiﬁcation, respectively. One can see that

good decomposition results cannot be obtained with-

out using edge classiﬁcation. Although deterministic

annealing offers no theoretical guarantee of ﬁnding

the global optimum, it is well known that it can avoid

many local minima (Geiger and Girosi, 1991; Ura-

hama and Nagao, 1995; Ueda and Nakano, 1998).

4 RESULTS

To demonstrate and evaluate our method, we used

real and synthetic images as inputs. First, we pho-

tographed a doll behind a glass window which was

reﬂected by the glass. Figure 6 shows the input image

(100x100 pixels). We extracted edges using the SU-

SAN edge detector (Figure 7(a)), thinned the edges

(Figure 7(b)), eliminated the crossing edges (Fig-

ure 7(c)) and classiﬁed each edge to which layer it

belongs (Figure 7(d)), as described in Section 2.1.

Using the estimated classiﬁcation of edges, we con-

structed an image pyramid from the input image and

decomposed the top most layer, as shown in Figure 8.

As shown in Figure 9, using this decomposition re-

sult as an initial guess, we decomposed the original

image into two images. This appears to be a quali-

tatively good result. In this case, we processed each

RGB channel separately.

Next, in order to evaluate the results of our method

quantitatively against ground truth, we used as input

the generated image by summing two already cap-

tured or synthetic images. Figures 10– 14 show the

input images, corresponding ground truth decompo-

sitions, and resulting decompositions. Figures 10 and

11 showexamples of using as inputs the generated im-

ages by summing two relatively simple images. One

can see that quite good results were obtained. Fig-

ures 12 and 13 show examples of using as inputs the

addition of simple and complex images. Despite some

undesired ghost images such as the baby’s face in Fig-

ure 12(c) and highlight in Figure 13(c), fairly good re-

sults seem to be obtained. Figure 14 shows an exam-

ple of using as an input the generated image by sum-

ming two relatively complex images. In Figure 14(c)

one can see several ghost images. The decomposition

algorithm roughly took about 15 minutes on a single

Pentium IV 2.4GHz processor.

Again, for the purpose of verifying the effec-

tiveness of the edge classiﬁcation described in Sec-

tion 2.1, we separated the input images in Fig-

ures 11(a), 13(a) without classifying edges, as at-

tempted in Figure 3(e). In both of these examples,

the image decomposition failed due to convergence at

local minima, as shown in Figure 15(a), (b). Those

examples demonstrate the signiﬁcance of classifying

edges for separating.

5 CONCLUSIONS

We proposed a novel method for decomposing a sin-

gle superimposed image into two images. Despite us-

ing neither image database nor user intervention, we

showed that the almost fully automatic layer extrac-

tion can be achieved using only a single input im-

age. One of the research problems to be solved in our

method is to provide robustness to errors in the edge

detection and classiﬁcation. We are currently study-

ing to adapt the different error recovery schemes.

REFERENCES

Farid, H. and Adelson, E. H. (1999). Separating reﬂec-

tions from images by use of independent components

analysis. JOSA, vol.16, no.9, pp.2136–2145.

Geiger, D. and Girosi, F. (1991). Parallel and deterministic

algorithms from mrf’s: Surface reconstruction. IEEE

PAMI, vol.13, no.5, pp.401–412.

Irani, M. and Peleg, S. (1992). Image sequence enhance-

ment using multiple motions analysis. Proc. IEEE

CVPR, pp.216–221.

Levin, A., Zomet, A., and Weiss, Y. (2002). Learning

to perceive transparency from the statistics of natural

scenes. IEEE NIPS.

Levin, A., Zomet, A., and Weiss, Y. (2004a). Separating

reﬂections from a single image using local features.

Proc. IEEE CVPR, pp.306–313.

Levin, A., Zomet, A., and Weiss, Y. (2004b). User assisted

separation of reﬂections from a single image using a

sparsity prior. Proc. ECCV, pp.602–613.

Sarel, B. and Irani, M. (2004a). Separating transparent lay-

ers of repetitive dynamic behaviors. Proc. IEEE ICCV,

pp.26–32.

Sarel, B. and Irani, M. (2004b). Separating transparent lay-

ers through layer information exchange. Proc. ECCV,

pp.328–341.

Schechner, Y., Shamir, J., and Kiryati, N. (2000). Blind re-

covery of transparent and semireﬂected scenes. Proc.

IEEE CVPR, pp.1038–1043.

Smith, S. M. and Brady, M. (1997). Susan -a new approach

to low level image processing. IJCV, vol.23, no.1,

pp.45–78.

Szeliski, R., Avidan, S., and Anandan, P. (2000). Layer

extraction from multiple images containing reﬂections

and transparency. Proc. IEEE CVPR.

Tsin, Y., Kang, S. B., and Szeliski, R. (2003). Stereo match-

ing with reﬂections and translucency. Proc. IEEE

CVPR, pp.702–709.

Ueda, N. and Nakano, R. (1998). Deterministic annealing

em algorithm. Neural Networks, vol.11, no.2, pp.272–

282.

Urahama, K. and Nagao, T. (1995). Direct analog rank ﬁl-

tering. IEEE Trans. Circuits Syst. I, vol.42, pp.385–

388.

Figure 6: Input image.

(a) (b)

Figure 7: Edge detection and classiﬁcation.

Figure 8: Intermediate result (decomposition on low reso-

lution image).

Figure 9: Decomposition.

(a) (b) (c)

Figure 10: Result. (a) Input image (synthesized by summing the simple images in b). (b) Ground truth images. (c) Decompo-

sition.

(a) (b) (c)

Figure 11: Result. (a) Input image (synthesized by summing the simple images in b). (b) Ground truth images. (c) Decompo-

sition.

(a) (b) (c)

Figure 12: Result. (a) Input image (synthesized by summing the complex and simple images in b). (b) Ground truth images.

(a) (b) (c)

Figure 13: Result. (a) Input image (synthesized by summing the complex and simple images in b). (b) Ground truth images.

(a) (b) (c)

Figure 14: Result. (a) Input image (synthesized by summing the complex images in b). (b) Ground truth images. (c)

Decomposition.

(a) (b)

Figure 15: Results without classifying edges. (a) Decomposition when the image of Fig. 11(a) is taken as an input. (b)

Decomposition when the separated green channel image of the image of Fig. 13(a) is taken as an input.