
MOTION INFORMATION COMBINATION FOR FAST HUMAN
ACTION RECOGNITION
Hongying Meng, Nick Pears
Department of Computer Science, University of York, York, UK
Chris Bailey
Department of Computer Science, University of York, York, UK
Keywords:
Event recognition, Human action recognition, Video analysis, Support Vector Machine.
Abstract:
In this paper, we study the human action recognition problem based on motion features directly extracted
from video. In order to implement a fast human action recognition system, we select simple features that
can be obtained from non-intensive computation. We propose to use the motion history image (MHI) as our
fundamental representation of the motion. This is then further processed to give a histogram of the MHI
and the Haar wavelet transform of the MHI. The processed MHI thus allows a combined feature vector to be
computed cheaply and this has a lower dimension than the original MHI. Finally, this feature vector is used in
a SVM-based human action recognition system. Experimental results demonstrate the method to be efficient,
allowing it to be used in real-time human action classification systems.
1 INTRODUCTION
Event detection in video is becoming an increasingly
important computer vision application, particularly in
the context of activity classification (Aggarwal and
Cai, 1999). Event recognition is an important goal
for building intelligent systems which can react to
what is going on in a scene. Event recognition is
also a fundamental building block for interactive sys-
tems which can respond to gestural commands, in-
struct and correct a user learning athletics, gymnastics
or dance movements, or interact with live actors in an
augmented dance or theatre performance.
Recognizing actions of human actors from digital
video is a challenging topic in computer vision with
many fundamental applications in video surveillance,
video indexing and social sciences. Feature extrac-
tion is the basis to perform many different tasks with
video such as video object detection, object tracking
and object classification.
Model based method are extremely challenging
as there is large degree of variability in human be-
haviour. The highly articulated nature of the body
leads to high dimensional models and the problem
is further complicated by the non-rigid behaviour
of clothing. Computationally intensive methods are
needed for nonlinear modeling and optimisation. Re-
cent research into anthropology has revealed that
body dynamics are far more complicated than was
earlier thought, affected by age, ethnicity, gender and
many other circumstances (Farnell, 1999).
Appearance-based models are based on the extrac-
tion of a 2D shape model directly from the images,
to be classified (or matched) against a trained one.
Motion-based models do not rely on static models of
the person, but on human motion characteristics. Mo-
tion feature extraction and selection are two of the key
components in these kinds of human action recogni-
tion systems.
In this paper, we study the human action classifi-
cation problem based on motion features directly ex-
tracted from video. In order to implement fast human
action recognition, we select simple features that can
be obtained from non-intensive computation. In par-
ticular, we use the Motion History Image (MHI) (Bo-
bick and Davis, 2001) as our fundamental feature. We
propose novel extraction methods to extract both spa-
tial and temporal information from these initial MHI
representations and we combine them as a new feature
vector that has a lower dimension and provides better
motion action information than the raw MHI informa-
tion. This feature vector was used in a Support Vector
21
Meng H., Pears N. and Bailey C. (2007).
MOTION INFORMATION COMBINATION FOR FAST HUMAN ACTION RECOGNITION.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 21-28
Copyright
c
SciTePress

Machine (SVM) based human action recognition sys-
tem.
The rest of this paper is organised as follows: In
section 2, we will give an introduction to some related
work. In section 3, we give a brief overview of our
system. In section 4, the detailed techniques of this
system are explained including motion features, fea-
ture extraction methods and SVM classifier. In sec-
tion 5, some experimental results are presented and
compared. Finally, we give the conclusions.
2 PREVIOUS WORK
Aggarwal and Cai (Aggarwal and Cai, 1999) present
an excellent overview of human motion analysis. Of
the appearance based methods, template matching has
increasingly gained attention. Bobick and Davis (Bo-
bick and Davis, 2001) use Motion Energy Images
(MEI) and Motion History Images (MHI) to recog-
nize many types of aerobics exercises. While their
method is efficient, their work assumes that the actor
is well segmented from the background and centred
in the image.
Schuldt (Schuldt et al., 2004) proposed a method
for recognizing complex motion patterns based on
local space-time features in video and demonstrated
such features can give good classification perfor-
mance. They construct video representations in terms
of local space-time features and integrate such rep-
resentations with SVM classification schemes for
recognition. The presented results of action recogni-
tion justify the proposed method and demonstrate its
advantage compared to other relative approaches for
action recognition.
Ke (Ke et al., 2005) studies the use of volumet-
ric features as an alternative to the local descriptor
approaches for event detection in video sequences.
They generalize the notion of 2D box features to 3D
spatio-temporal volumetric features. They construct a
real-time event detector for each action of interest by
learning a cascade of filters based on volumetric fea-
tures that efficiently scans video sequences in space
and time. This event detector recognizes actions that
are traditionally problematic for interest point meth-
ods such as smooth motions where insufficient space-
time interest points are available. Their experiments
demonstrate that the technique accurately detects ac-
tions on real-world sequences and is robust to changes
in viewpoint, scale and action speed.
Weinland (Weinland et al., 2005) introduces Mo-
tion History Volumes (MHV) as a free-viewpoint rep-
resentation for human actions in the case of multiple
calibrated, and background-subtracted, video cam-
eras. They present algorithms for computing, aligning
and comparing MHVs of different actions performed
by different people in a variety of viewpoints.
We note that the feature vector in these two meth-
ods is very expensive to construct and the learning
process is difficult, because it needs a big data set for
training.
Recently, Wong and Cipolla (Wong and Cipolla,
2005) proposed a new method to recognise primitive
movements based on the Motion Gradient Orientation
(MGO) image directly from image sequences. This
process extracts the descriptive motion feature with-
out depending on any tracking algorithms. By using
a sparse Bayesian classifier, they obtained good clas-
sification results for human gesture recognition.
Ogata (Ogata et al., 2006) proposed another effi-
cient technique for human motion recognition based
on motion history images and an eigenspace tech-
nique. In the proposed technique, they use Modified
Motion History Images (MMHI) feature images and
the eigenspace technique to realize high-speed recog-
nition. The experiment was performed on recogniz-
ing six human motions and the results showed satis-
factory performance of the technique. Note that the
eigenspace still needs to be constructed and some-
times this is difficult.
More recently, Dalal (Dalal et al., 2006) proposed
a Histogram of Oriented Gradient (HOG) appearance
descriptors for image sequences and developed a de-
tector for standing and moving people in video. In
this work, several different motion coding schemes
were tested and it was shown empirically that orien-
tated histograms of differential optical flow give the
best overall performance.
Oikonomopoulos (Oikonomopoulos et al., 2006)
introduced a sparse representation of image se-
quences as a collection of spatiotemporal events that
are localized at points that are salient both in space
and time for human actions recognition. They de-
tected the spatiotemporal salient points by measur-
ing the variations in the information content of pixel
neighborhoods not only in space but also in time and
derived a suitable distance measure between the rep-
resentations. Finally, they use Relevance Vector Ma-
chines (RVM) for classification.
These two methods need to detect salient points in
the frames and then make suitable features for classi-
fication. This implies significant computational cost
for detecting these points.
Meng (Meng et al., 2006b) proposed a fast sys-
tem for human action recognition which was based
on very simple features. They chose MHI, MMHI,
MGO and a linear classifier SVM for fast classifi-
cation. Experimental results showed that this sys-

tem could achieve good performance in human ac-
tion recognition. Further, they (Meng et al., 2006a)
proposed to combine two kinds of motion features
MHI and MMHI together and achieved better perfor-
mance in human action recognition based on a lin-
ear SVM
2K classifier (Meng et al., 2004) (Farquhar
et al., 2005). However, both these systems could only
work well in specific real-time applications with lim-
ited action classes because the overall performance on
real-world challenging database were still not good
enough.
3 OVERALL ARCHITECTURE
We propose a novel architecture for fast human action
recognition. In this architecture, a linear SVM was
chosen and MHI provided our fundamental features.
In contrast with the system in (Meng et al., 2006b), we
propose novel extraction methods to extract both spa-
tial and temporal information from these initial MHI
features and combine them in an efficient way as a
new feature vector that has lower dimension and pro-
vides better motion action information than the raw
MHI feature vector.
There are two reasons for choosing a linear SVM
as the classifier in the system. Firstly SVM is a clas-
sifier that has achieved very good performance in lots
of real-world classification problems. Secondly, SVM
can deal with very high dimensional feature vectors,
which means that there is plenty of freedom to choose
the feature vectors. Finally the classifier is able to op-
erate very quickly during the recognition process.
The overall architecture of the human action sys-
tem is shown in figure 1. There are two parts in this
system: a learning part and a classification part.
The MHI feature vectors are obtained directly
from human action video clips. The 2-D Haar wavelet
transform was employed to extract spatial information
within the MHI, while temporal information was ex-
tracted by computing the histogram of the MHI. Then
these two feature vectors were combined to produce a
lower dimensional and discriminative feature vector.
Finally, the linear SVM was used for the classification
process.
The learning part is processed using video data
collected off-line. After that, the obtained parameters
for the classifier can be used in a small, embedded
computing device such as a field-programmable gate
array (FPGA) or digital signal processor (DSP) based
system, which can be embedded in the application and
give real-time performance.
It should be mentioned here that, both 2-D Haar
wavelet transform and histogram of the MHI are
MHI Images
Training SVM
classifiers
Maintain the SVM's
parameters
Learning part Recognition part
Histogram
features
Haar wavelet
transform
Learning action
video clips
Combined
feature vectors
MHI Image
SVM classifiers
Recognizing the
action
Histogram
feature
Haar wavelet
transform
Input video clip
Combined
feature vector
Figure 1: SVM based human action recognition system.
In the learning part, the combined feature vector of Haar
wavelet transform and histogram of MHI were used for
training a SVM classifier, and the obtained parameters were
used in the recognition part.
achieved with very low computational cost. We only
keep the low-frequency part of the Haar wavelet trans-
form. So the total dimension of the combined feature
vector is lower than that of the original MHI feature.
4 DETAIL OF THE METHOD
In this section, we will give the detailed information
of the key techniques used in our human action recog-
nition system.
4.1 Motion Features
The recording of human actions usually needs large
amounts of digital storage space and it is time con-
suming to browse the whole video to find the required
information. It is also difficult to deal with this huge
data in detection and recognition. Therefore, several
motion features have been proposed to compact the
whole motion sequence into one image to represent
the motion. The most popular of these are the MHI,
MMHI and MGO. These three motion features have
the same size as the frame of the video, but they main-
tain the motion information within them. In (Meng
et al., 2006b), it has been found that MHI achieved
best performance in classification tests across six cat-
egories of action sequence.
A motion history image (MHI) is a kind of tempo-
ral template. It is the weighted sum of past successive
images and the weights decay as time lapses. There-
fore, an MHI image contains past raw images within
itself, where most recent image is brighter than past
ones.

Normally, an MHI H
τ
(u,v, k) at time k and loca-
tion (u,v) is defined by the following equation 1:
H
τ
(u,v, k) = {
τ if D(u,v,k) = 1
max{0,H
τ
(u,v, k) −1}, otherwise
(1)
where D(u,v,k) is a binary image obtained from
subtraction of frames, and τ is the maximum duration
a motion is stored. In general, τ is chosen as con-
stant 255 where MHI can be easily represented as a
grayscale image. An MHI pixel can have a range of
values, whereas the Motion Energy Image (MEI) is
its binary version. This can easily be computed by
thresholding H
τ
> 0 .
4.2 Histogram of Mhi
The histogram of the MHI has bins which record the
frequency at which each value (gray-level) occurs in
the MHI, excluding the zero value, which does not
contain any motion information of the action. Thus,
typically we will have bins between 1 and 255 pop-
ulated by one or more groupings, where each group-
ing of bins represents a motion trajectory. Clearly the
most recent motion is at the right of the histogram,
with the earliest motions recorded in the MHI being
more toward the left of the histogram. The spread
of each grouping in the histogram indicates the speed
of the motion, with narrow groupings indicating fast
motions and wide groupings indicating slow motions.
4.3 Haar Wavelet Transform
The Haar wavelet transform decomposes a signal into
a time-frequency field based on the Haar wavelet
function basis. For discrete digital signals, the dis-
crete wavelet transform can be implemented effi-
ciently by Mallat’s fast algorithm (Mallat, 1989). The
Mallat algorithm is in fact a classical scheme known
in the signal processing community as a two-channel
subband coder (see page 1 Wavelets and Filter Banks,
by Strang and Nguyen (Strang and Nguyen, 1996)).
The Mallat algorithm is used for both wavelet de-
composition and reconstruction. The algorithm has
a pyramidal structure with the underlying operations
being convolution and decimation. For a discrete sig-
nal s = (s
0
,s
1
,··· ,s
N−1
)(N = 2
L
,L ∈ Z
+
). For con-
venience, denote it as c
m,0
= s
m
,m = 0,1,··· , N −1.
Then Haar wavelet transform can be implemented by
the following iteration:
For l = 1,2,··· ,L and m = 0,1,··· , N/(l + 1)
c
m,l
=
1
∑
k=0
h
k
c
k+2m,l−1
d
m,l
=
1
∑
k=0
g
k
c
k+2m,l−1
(2)
where the h
0
,h
1
is low pass filter and g
0
,g
1
is
high pass filter:
h
0
= h
1
=
√
2,
g
0
=
√
2,g
1
= −
√
2
They are orthogonal:
g
k
= (−1)
k
h
1−k
(3)
and the obtained
{
c
.,L
,d
.,L
,d
.,L−1
,··· ,d
.,1
}
is the dis-
crete Haar wavelet transform of the signal.
An image is a 2-D signal and this 2-D space can be
regarded as a separable space, which means that the
wavelet transform on an image can be implemented
using a 1-D wavelet transform. On the same level, it
can be implemented on all the rows and then on all
the columns.
In this paper, we only keep the low-frequency part
of the Haar wavelet transform of the image. This part
can represent the spatial information of the MHI very
well in a lower dimension. The high-frequency infor-
mation is more useful for representing edges, which
is not really important in our system, and it is more
susceptible to noise. Actually, this part can be im-
plemented very quickly based on some specific algo-
rithms.
Figure 2 shows an example of a handwaving ac-
tion. (a) is the original video clip, (b) is the MHI, (c)
is the Haar wavelet transform of MHI where the red
square is low frequency part and (d) is Histogram of
the MHI.
4.4 Combining Features
The two feature vectors histogram of MHI and Haar
wavelet transform of MHI are combined in the sim-
plest way. The combined feature vector is built by
concatenating these two feature vectors into a higher
dimensional vector. In this way, the temporal and
spatial information of the MHI are integrated into
one feature vector while the dimension of the com-
bined feature vector has lower dimension in compari-
son with MHI itself.
4.5 Support Vector Machines
Support Vector Machines are a state-of-the-art clas-
sification technique with large application in a range

(a)
(b)
(c)
0 50 100 150 200 250
0
50
100
150
200
250
300
350
(d)
Figure 2: Motion feature of the action. (a) Original video
(b)MHI (c) Haar wavelet transform of MHI (d) Histogram
of MHI.
of fields including text classification, face recognition
and genomic classification, where patterns can be de-
scribed by a finite set of characteristic features.
We use the SVM for the classification component
of our system. This is due to SVM being an outstand-
ing classifier that has shown very good performance
on many real-world classification problems. Using ar-
bitrary positive definite kernels provides a possibility
to extend the SVM capability to handle high dimen-
sional feature spaces.
If the binary labels are denoted as y
i
, the norm-2
soft-margin SVM can be represented as a constrained
optimization
min
w,b,ξ
1
2
||w||
2
+C
∑
i
ξ
i
(4)
s.t.
h
x
i
,w
i
+ b ≥ 1−ξ
i
, y
i
= 1,
h
x
i
,w
i
+ b ≤ −1+ ξ
i
, y
i
= −1,
ξ
i
≥ 0,
where C is a penalty parameter and ξ
i
are slack vari-
ables. It can be converted by applying Langrange
multipliers into its Wolfe dual problem
max
α
i
L
D
≡
∑
i
α
i
−
1
2
∑
i, j
α
i
α
j
y
i
y
j
x
i
,x
j
(5)
s.t.
0 ≤ α
i
≤C,
∑
i
α
i
y
i
= 0.
The primal optimum solution for w can be repre-
sented as
w =
∑
i
α
i
y
i
x
i
. (6)
The weight vector w can be expressed as a linear
combination of the support vectors for which α
i
> 0.
It can be solved by quadratic programming methods.
The final hypothesis is:
h
w,b
(x) = sign(
h
w,x
i
+ b). (7)
It should be mentioned here that only dot products
of feature vectors appear in the dual of the optimiza-
tion problem. If we define the dot products as :
K(x
i
,x
j
) =
x
i
,x
j
. (8)
Then the dual problem can be represented by
max
α
i
L
D
≡
∑
i
α
i
−
1
2
∑
i, j
α
i
α
j
y
i
y
j
K(x
i
,x
j
),
0 ≤ α
i
≤C,
∑
i
α
i
y
i
= 0.
(9)
Based on this, the SVM can be generalized to the
case where the decision function is not a linear func-
tion of the data. Now suppose we first mapped the

data to some other(possibly infinite dimensional) Eu-
clidean space H, using a mapping which we call Φ:
Φ : R
d
7→ S. (10)
Then of course the training algorithm would only
depend on the data through dot products in S, i.e. on
functions of the form
Φ(x
i
),Φ(x
j
)
. We only need
to use K (Φ(x
i
),Φ(x
j
)) in the training algorithm and
we never need to explicitly know what Φ is.
Multiclass SVMs are usually implemented by
combining several two-class SVMs. In each binary
SVM, only one class is labelled as ”1” and the others
labelled as ”-1”. The one-versus-all method uses a
winner-takes-all strategy. If there are M classes, then
the SVM method will construct M binary classifiers
by learning. During the testing process, each classi-
fier will get a confidence coefficient and the class with
maximum confidence coefficient will be assigned to
this sample. In this paper, we will only use linear
SVMs in order to build a fast system.
5 EXPERIMENTAL RESULTS
5.1 Dataset
For the evaluation, we use a challenging human action
recognition database, recorded by Christian Schuldt
(Schuldt et al., 2004). It contains six types of hu-
man actions (walking, jogging, running, boxing, hand
waving and hand clapping) performed several times
by 25 subjects in four different scenarios: outdoors
(s1), outdoors with scale variation (s2), outdoors with
different clothes (s3) and indoors (s4).
This database contains 2391 sequences. All se-
quences were taken over homogeneous backgrounds
with a static camera with 25Hz frame rate. The se-
quences were down-sampled to the spatial resolution
of 160×120 pixels. For all the action sequences, the
length of the sequences are vary and the average is
four seconds (about 100 frames). To the best of our
knowledge, this is the largest video database with se-
quences of human actions taken over different scenar-
ios. All sequences were divided with respect to the
subjects into a training set (8 persons), a validation
set (8 persons) and a test set (9 persons). In our ex-
periment, the classifiers were trained on the training
set while classification results were obtained on the
test set.
Figure 3 showed six types of human actions in the
database: walking, jogging, running, boxing, hand-
clapping and handwaving. Row (a) are the original
videos, (b) and (c) are the associated MHI and His-
togram of MHI features.
(a)
(b)
(c)
0 50 100 150 200 250
0
100
200
300
400
500
600
700
0 50 100 150 200 250
0
100
200
300
400
500
600
700
800
900
0 50 100 150 200 250
0
200
400
600
800
1000
1200
0 50 100 150 200 250
0
50
100
150
0 50 100 150 200 250
0
20
40
60
80
100
120
140
0 50 100 150 200 250
0
50
100
150
200
250
300
350
Figure 3: Six types of human actions in the database: walk-
ing, jogging, running, boxing, handclapping and handwav-
ing. Row (a) are the original videos, (b) and (c) are associate
MHI and Histogram of MHI features.
5.2 Experimental Setup
Our experiments were carried out on all four differ-
ent scenarios: outdoors, outdoors with scale variation,
outdoors with different clothes and indoors. In the
same manner as paper (Ke et al., 2005), each sequence
is treated individually during the training and classifi-
cation process. In all the following experiments, the
parameters were chosen to be the same. The threshold
in differential frame computing was chosen as 25 and
τ was chosen as constant 255 for MHI construction.
A MHI was calculated from each action sequence
with about 100 frames. The size of each MHI is
160 ×120 = 19200, which is same width as that of
the frames in the videos. The values of MHI are in the
interval of [0, 255]. Then each MHI was decomposed
using a 2-D Haar wavelet transform to L = 3 levels.
Thus the size of the low frequency part of the Haar
wavelet transform of MHI is 20 ×15 = 300. Since
the length of the histogram of MHI is 255, the length
of combined feature vector is 555.
In our system, each SVM was trained based on
features obtained from human action video clips in
a training dataset. These video clips have their own
labels such as ”walking,” ”running” and so on. In
classification, we actually get a six-class classifica-
tion problem. At first, we create six binary SVM clas-
sifiers, and each of them is related to one of the six
classes. For example, there is one SVM classifier re-
lated to the class ”walking.” In the training dataset,
the video with label ”walking” will have a label ”1”
in SVM classifier while all others have a label ”-1” in
the SVM. Secondly, we will train these SVM classi-
fiers on the learning dataset. The SVM training can
be implemented using programs freely available on
the web, such as SVM
light
(Joachims, 1999). Finally,
we obtained several SVM classifiers with associated
parameters.
In the recognition process, feature vectors will be
extracted from the input human action video sample.
Then all the SVM classifiers obtained from the train-
ing process will classify the extracted feature vector.
Finally, the class with maximum confidence coeffi-
cient within these SVM classifiers will be assigned to
this sample.
5.3 Experiment Results
Tables 1 show the classification confusion matrix
based on the method proposed in paper (Ke et al.,
2005).The confusion matrices show the motion label
(vertical) versus the classification results (horizontal).
Each cell (i, j) in the table shows the percentage of
class i action being recognized as class j. Then trace
of the matrices show the percentage of the correctly
recognized action, while the remaining cells show the
percentage of misclassification.
Table 1: Ke’s confusion matrix, trace=377.8.
Walk Jog Run Box Clap Wave
Walk 80.6 11.1 8.3 0.0 0.0 0.0
Jog 30.6 36.2 33.3 0.0 0.0 0.0
Run 2.8 25.0 44.4 0.0 27.8 0.0
Box 0.0 2.8 11.1 69.4 11.1 5.6
Clap 0.0 0.0 5.6 36.1 55.6 2.8
Wave 0.0 5.6 0.0 2.8 0.0 91.7
Table 2: MHI S’s confusion matrix, trace=377.7.
Walk Jog Run Box Clap Wave
Walk 56.9 18.1 22.2 0.0 0.0 2.8
Jog 45.1 29.9 22.9 1.4 0.0 0.7
Run 34.7 27.8 36.1 0.0 0.0 1.4
Box 0.0 0.0 0.0 89.5 2.1 8.4
Clap 0.0 0.0 0.0 5.6 88.9 5.6
Wave 0.0 0.0 0.0 12.5 11.1 76.4
Table 3: MHI hist’s confusion matrix, trace=328.6.
Walk Jog Run Box Clap Wave
Walk 62.5 32.6 0.0 1.4 1.4 2.1
Jog 12.5 58.3 25.0 0.0 0.0 4.2
Run 0.7 18.8 77.1 0.0 0.0 3.5
Box 4.9 2.8 0.7 17.5 61.5 12.6
Clap 4.9 2.1 0.7 11.1 75.0 6.3
Wave 5.6 3.5 6.9 20.1 25.7 38.2
In order to study the performance of the Haar
wavelet transform of MHI and histogram of MHI, we
used linear SVM classifier on them separately and
compared their performance. Table 2 and table 3
shows the confusion matrix obtained for Haar wavelet
transform and histogram of MHI separately. From
these two tables, it can be seen that Haar wavelet
transform of MHI obtains a similar performance to
Ke’s method. This feature did very well in distin-
guishing the last three groups. On the other hand,
histogram of MHI did not do well on overall perfor-
mance. But it has the power to distinguish the first
three groups. That demonstrates that they keep differ-
ent information from the Haar wavelet of MHI.
Table 4 show the confusion matrix obtained from
our system in which combined feature were used.
From this table, we can see that the overall perfor-
mance has got a significant improvement on Ke’s
method based on volumetric features. Good perfor-
mance is achieved in distinguishing all of the six ac-
tions in the dataset.
Table 4: MHI
S&MHI hist’s confusion matrix,
trace=425.6.
Walk Jog Run Box Clap Wave
Walk 68.8 11.1 17.4 0.0 0.0 2.8
Jog 36.8 36.1 25.0 1.4 0.0 0.7
Run 14.6 20.1 63.9 0.0 0.0 1.4
Box 0.0 0.0 0.0 89.5 2.1 8.4
Clap 0.0 0.0 0.0 4.9 89.6 5.6
Wave 0.0 0.0 0.0 11.1 11.1 77.8
It should be mentioned here that in paper (Schuldt
et al., 2004), the performance is slightly better where
trace=430.3. But our system was trained in the
same way as (Ke et al., 2005) to detect a single in-
stance of each action within arbitrary sequences while
Schuldt’s system has the easier task of classifying
each complete sequence (containing several repeti-
tions of same action) into one of six classes.
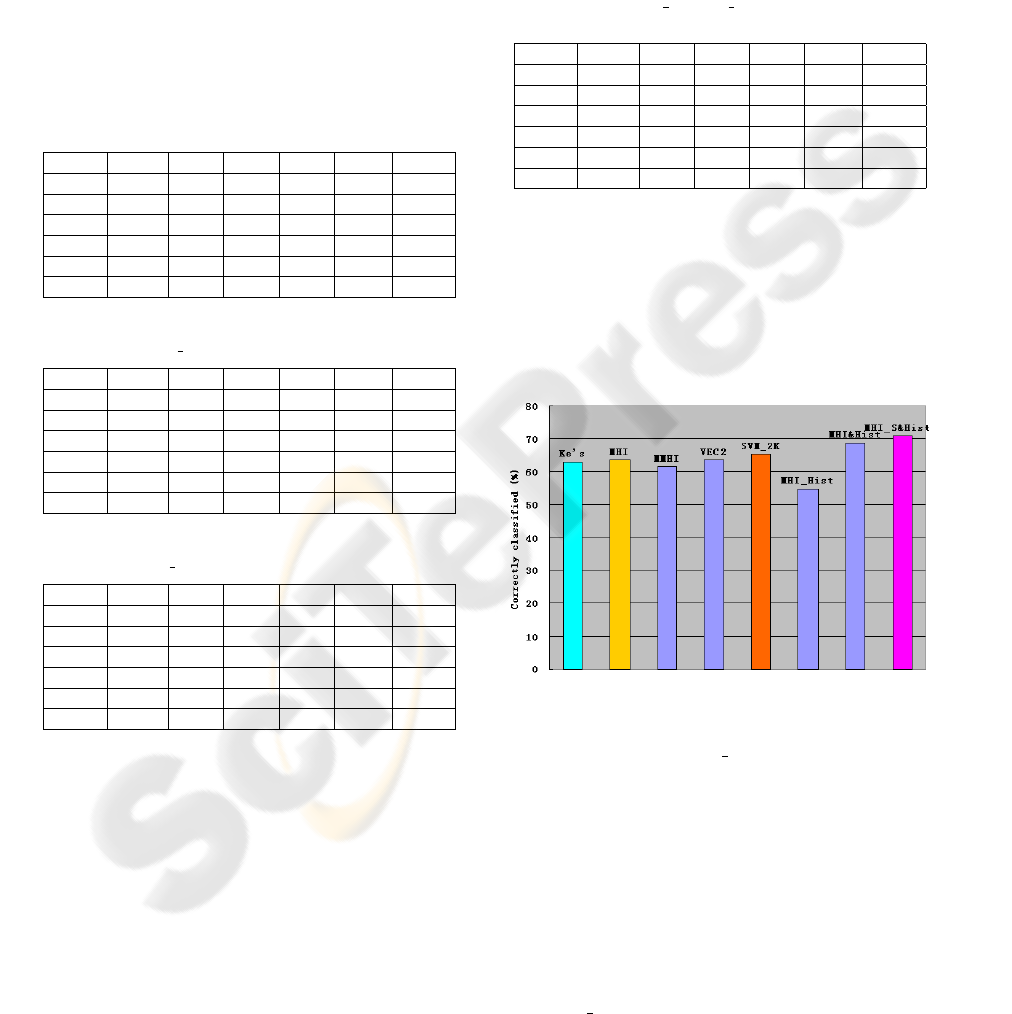
Figure 4: Comparison results on the correctly classified rate
based on different methods: Ke’s method; SVM on MHI;
SVM on MMHI; SVM on the concatenated feature (VEC2)
of MHI and MMHI and SVM
2K on MHI and MMHI;SVM
on histogram of MHI; SVM on the combined feature of
MHI and histogram of MHI; SVM on combined feature of
Haar wavelet transform of MHI and histogram of MHI.
We also compared the correctly classified rate
based on our system with other previous results in
the figure 4. The first one is the Ke’s method, the
second, third and sixth are SVM based on individ-
ual features MHI, MMHI and Histogram of MHI re-
spectively. The fourth one is SVM based on com-
bined feature from MHI and MMHI. The fifth is us-
ing SVM
2K classifier on both MHI and MMHI. The

seventh is SVM on combined feature from MHI and
its histogram. The last one is the results SVM based
on Haar wavelet transform of MHI and histogram of
MHI. This last result achieves the best overall perfor-
mance of approximately 71% correct classification.
6 CONCLUSION
In this paper, we proposed a system for fast human ac-
tion recognition. Potential applications include secu-
rity systems, man-machine communication, and ubiq-
uitous vision systems. The proposed method does
not rely on accurate tracking as many other works
do, since many tracking algorithms incur a prohibitive
computational cost for the system. Our system is
based on simple features in order to achieve high-
speed recognition, particularly in real-time embedded
vision applications.
In comparison with local SVM methods by
Schuldt (Schuldt et al., 2004), our feature vector is
much easier to obtain because we don’t need to find
interest points in each frame. We also don’t need a
validation dataset for parameter tuning.
In comparison with Meng’s (Meng et al., 2006b)
(Meng et al., 2006a) methods, we use a Haar wavelet
transform and histogram methods to build a new fea-
ture vector from the MHI representation. This new
feature vector contains the important information of
the MHI and also has a lower dimension. Experimen-
tal results demonstrate that these techniques made a
significant improvement on the human action recog-
nition performance compared to other methods.
If the learning part of the system is conducted off-
line, this system has great potential for implementa-
tion in small, embedded computing devices, typically
FPGA or DSP based systems, which can be embedded
in the application and give real-time performance.
REFERENCES
Aggarwal, J. K. and Cai, Q. (1999). Human motion
analysis: a review. Comput. Vis. Image Underst.,
73(3):428–440.
Bobick, A. F. and Davis, J. W. (2001). The recognition
of human movement using temporal templates. IEEE
Trans. Pattern Anal. Mach. Intell., 23(3):257–267.
Dalal, N., Triggs, B., and Schmid, C. (2006). Human de-
tection using oriented histograms of flow and appear-
ance. In LNCS, volume 3952. ECCV 2006.
Farnell, B. (1999). Moving bodies, acting selves. Annual
Review of Anthropology, 28:341–373.
Farquhar, J. D. R., Hardoon, D. R., Meng, H., Shawe-
Taylor, J., and Szedmak, S. (2005). Two view learn-
ing: Svm-2k, theory and practice. In NIPS.
Joachims, T. (1999). Making large-scale svm learning prac-
tical. In Advances in Kernel Methods - Support Vector
Learning, USA. MIT-Press. Oikonomopoulos, Anto-
nios and Patras, Ioannis and Pantic, Maja eds.
Ke, Y., Sukthankar, R., and Hebert., M. (2005). Efficient vi-
sual event detection using volumetric features. In Pro-
ceedings of International Conference on Computer Vi-
sion, pages 166–173. Beijing, China, Oct. 15-21,
2005.
Mallat, S. (1989). A theory for multiresolution signal de-
composition: the wavelet representation. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
11:674–693.
Meng, H., Pears, N., and Bailey, C. (2006a). Human action
classification using svm
2k classifier on motion fea-
tures. In Lecture Notes in Computer Science (LNCS),
volume 4105, pages 458–465, Istanbul, Turkey. Inter-
national workshop on Multimedia Content Represen-
tation,Classification and Security (MRCS 2006).
Meng, H., Pears, N., and Bailey, C. (2006b). Recogniz-
ing human actions based on motion information and
svm. In 2nd IET International Conference on Intel-
ligent Environments, pages 239–245, Athens, Greece.
IET.
Meng, H., Shawe-Taylor, J., Szedmak, S., and Farquhar, J.
D. R. (2004). Support vector machine to synthesise
kernels. In Deterministic and Statistical Methods in
Machine Learning, pages 242–255.
Ogata, T., Tan, J. K., and Ishikawa, S. (2006). High-speed
human motion recognition based on a motion history
image and an eigenspace. IEICE Transactions on In-
formation and Systems, E89(1):281–289.
Oikonomopoulos, A., Patras, I., and Pantic, M. (2006).
Kernel-based recognition of human actions using spa-
tiotemporal salient points. In Proceedings of IEEE
Int’l Conf. on Computer Vision and Pattern Recogni-
tion 2006, volume 3.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recogniz-
ing human actions: a local SVM approach. In Proc.
Int. Conf. Pattern Recognition (ICPR’04), Cambridge,
U.K.
Strang, G. and Nguyen, T. (1996). Wavelets and Filter
Banks. Wellesley Cambridge Press.
Weinland, D., Ronfard, R., and Boyer, E. (2005). Motion
history volumes for free viewpoint action recognition.
In IEEE International Workshop on modeling People
and Human Interaction (PHI’05).
Wong, S.-F. and Cipolla, R. (2005). Real-time adaptive
hand motion recognition using a sparse bayesian clas-
sifier. In ICCV-HCI, pages 170–179.
