
RECONSTRUCTING WAFER SURFACES WITH MODEL BASED
SHAPE FROM SHADING
Alexander Nisenboim
Israel Institute of Technology, Applied Mathematics Dept., Haifa, Israel
Alfred Bruckstein
Israel Institute of Technology, Comuter Science Dept., Haifa, Israel
Keywords:
Shape from shading, wafer, scanning electron microscope, mathematical model, wavelets, non-linear opti-
mization.
Abstract:
Model based Shape From Shading (SFS) is a promising paradigm introduced by J. Atick for solving such
inverse problems when we happen to have some prior information on the depth profiles to be recovered. In the
present work we adopt this approach to address the problem of recovering wafer profiles from images taken
by a Scanning Electron Microscope (SEM). This problem arises naturally in the microelectronics inspection
industry. A low dimensional model based on our prior knowledge of the types of depth profiles of wafer
surfaces has been developed and based on it the SFS problem becomes an optimal parameter estimation.
Wavelet techniques were then employed to calculate a good initial guess to be used in Levenberg-Marguardt
(LM) minimization process that yields the desired profile parametrization. The proposed algorithm has been
tested under both Lambertian and SEM imaging models.
1 INTRODUCTION
The problem of recovering a 3D object’s shape from
its shaded image, namely the Shape From Shading
(SFS) problem, has intrigued the computer vision re-
searchers for more then 30 years. The research in this
area was mostly inspired by the fact that our brain has
an outstanding ability to perceive the depth of the ob-
served scene from 2D images on the retina. Shading
is only one of the clues used by our brain to do the job.
It is interesting that despite the lack of our understand-
ing of this cognitive feature and major difficulties of
our mathematical modeling attempts, nowadays there
is a need for SFS-based applications in some branches
of the computer industry. Manufacturing of integrated
circuit wafers is an expensive and delicate process
and a great deal of effort is invested in the control of
quality and acceptability of such crucial device fea-
tures as contact holes, tracks etc. Typically, the man-
ufacturers are interested in measuring the geometri-
cal parameters of the features and due to the ”nano-
sizes” of the structures studied, the non-destructive
Low-Voltage SEM is used. Thus, the necessity of
3D-surface measurements from 2D SEM images nat-
urally arises. The very nature of the SFS idea is to
exploit the fact that the variations of surface’s orien-
tation cause the variations of the brightness at corre-
sponding areas in the image. However, the brightness
only carries information about the projection of sur-
face normal on the light source direction (see eq. (1)
) and hence the surface normal at each point cannot
be uniquely discovered. Thus, mathematically speak-
ing, the SFS problem appears to be ill-posed, however
recent interesting reformulations challenge this view-
point (Prados et al., 2004). One way to overcome
these fundamental difficulties is to reformulate the
SFS as a variational problem while introducing reg-
ularization terms into the minimized functional (Horn
and Brooks., 1986), (Zheng and Chellappa, 1991).
There are also alternative general approaches using
facet model (T. Pong and Shapiro., 1989), level sets
(R. Kimmel and Bruckstein., 1995) or hierarchical
representations (A. Jones, 1994). However, being
general, these approach could suffer from some draw-
backs (A. Jones, 1994). In this work, following a
paradigm introduced by J. Atick (Atick et al., 1996),
we try to directly use a priori information about the
geometry of the studied surfaces. Giving up gener-
333
Nisenboim A. and Bruckstein A. (2007).
RECONSTRUCTING WAFER SURFACES WITH MODEL BASED SHAPE FROM SHADING.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 333-340
Copyright
c
SciTePress

ality, we assume a model of the surface controlled
by a finite set of parameters. The resulting para-
meter estimation SFS problem appears to be simpler
than the original one. The initial estimates are ob-
tained by means of analysis of the wavelet decom-
position of the given image and subsequently a para-
meter fitting process is carried out. Finally, an itera-
tive LM minimization procedure has been adopted in
our work in order to insure stable numerical conver-
gence. It should be mentioned here that this research
was initiated and partially sponsored by Applied Ma-
terials,Inc., so the real data is banned from being pub-
lished due to its high business sensitivity. Therefore
the whole method is explained using a synthetic but
illustrative example. This paper is organized as fol-
lows. In Section 2 we mathematically formulate the
SFS problem and briefly overview the previous rele-
vant work. Section 3 contains the description of the
new method. Section 4 presents results and discus-
sion.
2 THE SHAPE FROM SHADING
PROBLEM
2.1 General Problem Setup
The monocular SFS problem is defined as follows.
Suppose we are looking for a smooth height field
z = z(x,y) over region D ⊂ R
2
, and we are given its
shaded image I(x,y). The value of I at each point
depends on reflectance properties of the surface, its
gradient and imaging geometry parameters like light
direction e.t.c. This dependence is called a reflectance
function, and we denote it R = R(p,q), where p = z
x
and q = z
y
. The relationship
I(x, y) = R(p(x,y),q(x,y)) (1)
is called the irradiance equation and we state the SFS
problem as an attempt to recover the surface height
field z(x,y) from a single shaded image I(x, y) given
the reflectance function R, i.e. to determine z(x,y) that
satisfies (1). Some assumptions are to be made about
imaging geometry. First, we assume that the size of
the studied object is small, compared to the viewing
distance, which enables us to presume orthographic
projection to the image plane. We also assume that
the camera direction coincides with the Z axis. In this
case one can choose the coordinate system of both
image and object planes to be identical and denoted
by (X,Y). We denote η to be composite albedo which
essentially captures the energy dissipation properties
of the surface. We assume that η is constant along the
surface. We also denote
~
L to be the unit vector of the
illumination direction. We assume that there is only
one source of light located at infinity.
2.2 Imaging Models
By definition, if R(p,q) = η < ~n(x,y),
~
L > we say
that a surface exhibits Lambertian diffuse reflection
property. Here <,> is a standard inner product and
~n(x,y) = (−p,−q,1)/
p
p
2
+ q
2
+ 1 is a unit normal
vector to the surface. In case of SEM, the sim-
plest image formation model is given by R(p,q) =
η/<~n(x,y),
~
L >. This model holds well when spec-
imen is coated by gold and in absence of charging
artifacts (Reimer, 1993). It turns out that the prob-
lem of computing η and
~
L can be solved separately
(Zheng and Chellappa, 1991) and, therefore, we sup-
pose them to be known. We should note here that the
algorithm presented below in no way depends on any
particular imaging model.
2.3 Previous Work
The problem of SFS was stated by B. Horn in 70’s
(Horn, 1975). His first solution involved characteris-
tic strips expansion of the irradiance equation (1) and
was not stable in practice due the noise sensitivity and
error accumulation problems. During 80’s, Horn and
others (Horn and Brooks., 1986), (Zheng and Chel-
lappa, 1991) reformulated the problem and solved it
using the calculus of variations. Nice and comprehen-
sive analysis of other SFS techniques can be found
in (Zhang et al., 1999). Another important idea was
suggested by J. Atick (Atick et al., 1996). In this
work the authors dealt with the problem of recovering
of the shape of human faces from their shaded images.
In order to employ the a priori information about the
class of objects studied, Atick gives up generality (of
the variational approach) and solves the SFS prob-
lem for this particular class. The exact laser scans of
200 faces represented in a cylindrical coordinate sys-
tem {r
i
(θ,l)}
200
i=1
where regarded as independent re-
alizations of some stochastic process. Thus a ”face-
surface” can be represented as
r(θ,l) = r
0
(θ,l) +
M
∑
i=1
a
i
u
i
(θ,l) (2)
where r
0
(θ,l) is a ”mean-face”, and u
i
(θ,l) are the
first M components of Karhunen-Loeve decompo-
sition derived from the scanned surfaces, so-called
”eigen-faces”. So, denoting
~
α = (α
1
,α
2
,... ,α
M
) the
SFS problem can be reformulated as
min
~
α
∑
l,θ
(I(x(l,θ),y(l,θ)) − R(p, q;
~
α))
2
(3)

This basically means that we are looking for the best
coefficients of the linear combination of the ”eigen-
faces” that explain our input image in terms of mean
square error. Thus the SFS problem becomes one of
optimal parameter estimation and it has been solved
using gradient descent method.
3 MODEL BASED SFS FOR
WAFERS
3.1 A Priori Knowledge
Unlike the work of J. Atick mentioned above, with
surfaces of wafers no statistical information is avail-
able. Therefore we concentrate our efforts to employ
a priori knowledge about wafer geometry in attempt
to work out low-dimensional and meaningful repre-
sentations of wafer surfaces. Wafer surface could be
characterized as a plane with a set of mutually dis-
joint contact holes and tracks (Figure 1) which should
subsequently be filled with conducting matter. These
tracks might be either straight or bent. One can as-
sume that the edges of holes and tracks are parallel to
the X and/or Y axes of the image plane. This assump-
tion does not always hold in practice, but its violation
is rather rare and hence disregarded in our model. The
shape of holes may vary with their size. Holes of rel-
atively large size look like a rectangle with somewhat
rounded corners and edges which are normally par-
allel to the axes. However, smaller holes assumed to
have rather rounded shape like ellipses or circles. One
cannot assume that slopes of holes and tracks are sym-
metrical. In the next section we define mathematical
objects which fit well the geometry described above.
0
20
40
60
80
100
120
140
0
20
40
60
80
100
120
140
−1.5
−1
−0.5
0
Figure 1: Wafer surface.
3.2 Mesa Function
We start with the following formal construction of a
so-called mesa (table) function. Let us define
f(x;x
0
,ε) =
cexp
1
1−
x−x
0
ε
2
!
, |x− x
0
| < ε
0 , elsewhere
(4)
The constant c in this definition is such that
x
0
+ε
x
0
−ε
f(x;x
0
,ε)dx = 1 (5)
Then a mesa function is then defined as
F(x;x
r
,ε
r
,x
l
,ε
l
) =
x
−∞
( f(t;x
l
,ε
l
) − f(t;x
r
,ε
r
))dt
(6)
The parameters of mesa function have simple geomet-
rical interpretation:
1. |x
r
− x
l
| is responsible for the size of the ”pulse”.
2. ε
r
,ε
l
control the slopes of the function.
Now, let us define 2D mesa function of height h to be
h times tensor product of two 1D mesa functions. For
simplicity we denote
~
α
x
= (x
r
,ε
xr
,x
l
,ε
xl
);
~
α
y
= (y
r
,ε
yr
,y
l
,ε
yl
)
~
α = (x
r
,ε
xr
,x
l
,ε
xl
,y
r
,ε
yr
,y
l
,ε
yl
,h) = (
~
α
x
,
~
α
y
,h)
and then
T(x,y;
~
α) = h · F(x;
~
α
x
) · F(y;
~
α
y
)
See Figure 2.
0
20
40
60
80
100
120
140
0
50
100
150
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Figure 2: 2D mesa function.

3.3 Surface Representation
By means of 2D mesa functions we can build success-
ful representations of surfaces of the type described
in the previous section. Indeed, a straight track or
hole feature can be represented as a negative 2D mesa
function. A bent track, for example, can be con-
structed as difference of two 2D mesa functions when
one of them is shifted from another. Therefore we can
write
z(x,y) =
N
∑
i=1
T
i
(x,y), (7)
when
T
i
(x,y) = T(x,y;
~
α
i
)
which means that in terms of this model, SFS prob-
lem becomes one of optimal parameter estimation. In
the following sections we shall develop a technique
to separate between the features and find N initial sets
of parameters (along with N itself) for each feature
instead attempting to estimate them all together.
3.4 Strategy
It is well known that in order to succeed in the mini-
mization process mentioned above a good initial es-
timate is needed. Let us briefly describe our main
strategy. It is very common practice to take into
account prior knowledge about image structure (like
edge-geometry, or statistics of the noise e.t.c.) to sim-
plify the very complex tasks of image processing and
analysis. In our case, the surface model implies a
certain geometrical structure of the image. First, all
edges are straight and parallel to the axes. Second,
the edges are expected to be organized in well-defined
constellations. For example, in case of an image of
a relatively large contact hole, its edges will tend to
form a rectangular shape. See Figure 3. Therefore, by
decomposing the image in Haar wavelets basis, and
picking the largest amplitude coefficients one can get
compact and effective representation of image singu-
larities. Moreover, large Haar coefficients will carry
the spatial information of image singularities at each
level of the decomposition. Since image singularities
form well-organized clusters, so do the large ampli-
tude wavelet coefficients.Thus the wavelets represen-
tation properties could be exploited in order to local-
ize every surface feature from its coefficients cluster
and roughly calculate its parameter vector.This vector
will subsequently serve as the starting point for the
Least Square Error (LSE) optimization process and
iteratively refined toward the final result.
Two points are worth mentioning. First, applying this
strategy we will separate surface features and treat
20 40 60 80 100 120
20
40
60
80
100
120
Figure 3: Lambertian image of the surface shown on Fig-
ure 1.
them independently which solves the problem of un-
known number of terms in model (7). Second, the ini-
tial parameter estimates are geometrically meaningful
which significantly reduces our chances to fall into
some local minima during the LSE procedure. Let us
elaborate on this strategy in the following sections.
3.5 Haar Wavelets for Tracking
Singularities
The expansion of I(x, y) ∈ L
2
(R
2
) in the orthonormal
basis of Haar functions
Ψ
1
j,n
,Ψ
2
j,n
,Ψ
3
j,n
j∈Z,n∈Z
2
I(x, y) =
3
∑
k=1
∞
∑
j= −∞
∑
n
w
k
j,n
Ψ
k
j,n
(8)
where
w
k
j,n
=
D
f,Ψ
k
j,n
E
will be referred as Discrete Haar Transform (DHT)
and it has an interpretation in terms of image details
aggregation at all resolution levels that range from 0
to +∞, (Mallat, 1999). The inner products w
1
j,n
repre-
sent details in the horizontal direction, w
2
j,n
give the
details in vertical direction and w
3
j,n
are the details in
both directions (corners)(Fig. 4). It is suitable rec-
tangular shape of Haar functions which makes them
appealing to our model, since they should correlate
well with mesa functions.Suppose that at each res-
olution scale s three binary images H
s
, V
s
and D
s
,
are produced (Fig. 5). The images are built from
the large amplitude coefficients corresponding to hor-
izontal, vertical and diagonal directions by means of
binarization process. For any binary image B we de-
note CC(B) = {CC
i
(B)} to be the set of connected
components of B. Then let us define a Feature Track-
ing Graph (FTG) G
s
using the following definitions:
1. The set of vertices of G
s
is equal to the set
CC(D
s
).
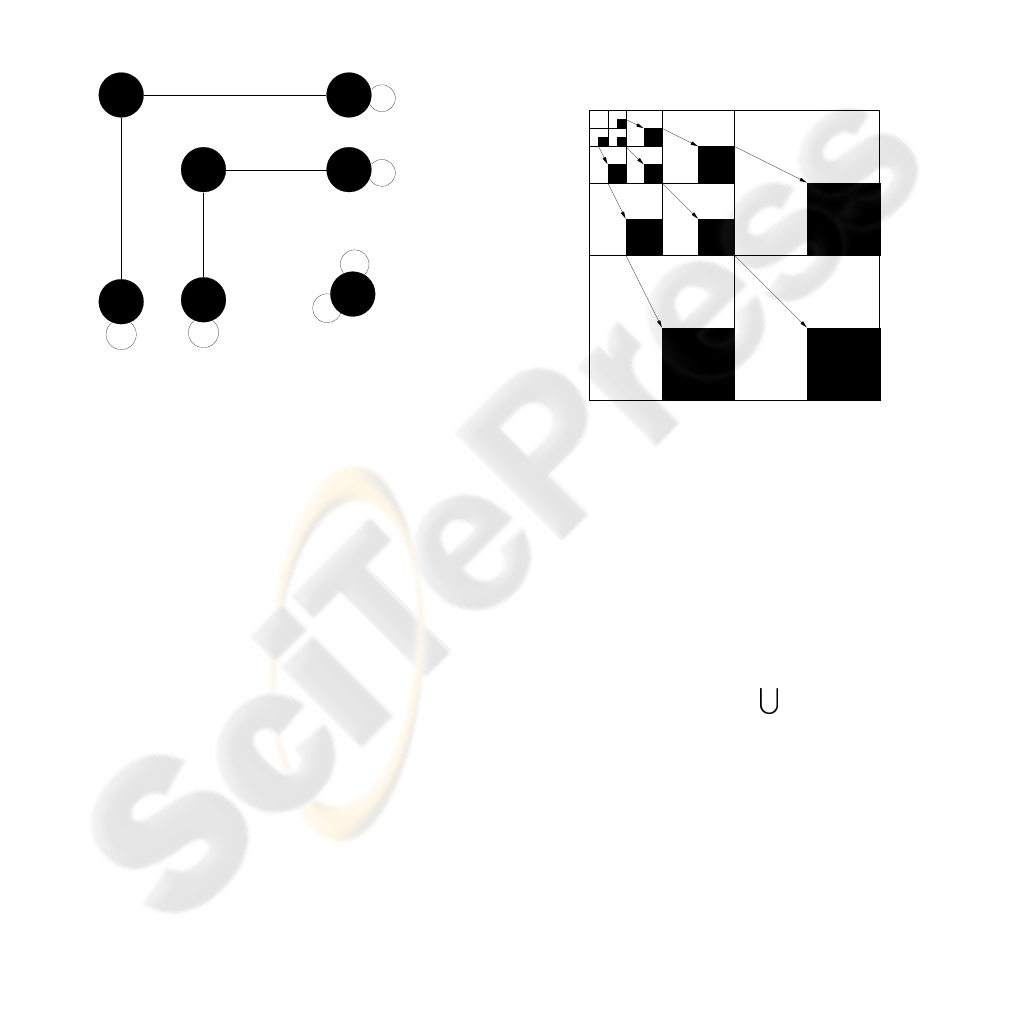
2. The unordered pair (v
p
,v
q
) of vertices is said to
be H-type edge if
∃k : CC
p
(D
s
) ∩CC
k
(H
s
) 6= 0
and
CC
q
(D
s
) ∩CC
k
(H
s
) 6= 0
or V-type edge if
∃k : CC
p
(D
s
) ∩CC
k
(V
s
) 6= 0
and
CC
q
(D
s
) ∩CC
k
(V
s
) 6= 0
H
H
V
V
V
H
V
V
H
H
Figure 6: FTG built from the images illustrated on Fig 5.
Note that the operation ∩ should be redefined here
because, CC
p
(D
s
) and, for example,CC
k
(H
s
) are em-
bedded in different images. One can imagine that H
s
,
V
s
and D
s
are placed ”one on top of the other”, or in
other words, they share the same coordinate system.
In this sense the operation ∩ is well defined. Uncon-
nected FTG G
s
can be decomposed to the set of N
connected subgraphs G
s
= {CSG
i
(G
s
)}
N
i=1
by means
of any standard method. Decomposition of FTG in
connected subgraphs naturally reflects the geometri-
cal structure of singularities at each level of reso-
lution. For each CSG
i
(G
s
) it is possible to locate
the spatial position of the surface singularities which
originated the coefficientsthatCSG
i
(G
s
) is built from,
and hence the number N of connected subgraphs is
our estimate of number of terms in model (7). In or-
der to trace the location of surface features we need
a notion of the Spatial Orientation Trees (SOT) bor-
rowed from the work of Shapiro (Shapiro., 1986). In
this work so-called Zero Tree (ZT) have been used as
a tool to optimize the transformation coefficients cod-
ing. Here we slightly modify ZT construction in order
to adopt it to our goals. For each spatial orientation
k = 1,2,3 we create quad-trees by relating recursively
each coefficient at the scale s and position (p,q), say
w
k
s
(p,q), to its four children at the next, finer, scale
s+ 1: w
k
s+1
(2p,2q),w
k
s+1
(2p + 1,2q),w
k
s+1
(2p,2q +
1),w
k
s+1
(2p + 1,2q + 1) Usually, the branching rule
of the coefficients at the most coarse scale, say s = 0,
is different. Each coefficient w
0
0
(p,q) is associated
with the three wavelet coefficients at the same scale
and location: w
1
0
(p,q), w
2
0
(p,q), w
3
0
(p,q), and con-
sidered to be the roots of the trees.We artificially at-
tach the image planes to each spatial orientation. The
reason behind it is that we are going to use not the val-
ues of the pixels, but only their absolute coordinates.
The ”pseudo-coefficients”at this artificial level on the
image plane will be considered as the leaves of the
trees. The construction of SOT is illustrated in Fig-
ure 7. Note that if at some scale level s and position
Image Plane Image Palne
Image Plane
S = 0
S = 1
S = 2
S = 3
ROI
ROIROI
Figure 7: Spatial Orientation Tree.
(p,q) there is a wavelet coefficient w
k
s
(p,q) of high
amplitude, then all image singularities which possibly
contributed to the coefficient are likely to be included
into the spatial area of the leaves of the SOT rooted at
(s, p,q). Let us denote it as the region of influence of
w
k
s
(s, p,q) by ROI(s, p,q), see Figure 7. Clearly, the
wavelet coefficients w
1
s
(p,q), w
2
s
(p,q) and w
3
s
(p,q)
have the same ROI. Now, the ROI of each connected
subgraph can be defined as
ROI(CSG
i
(G
s
)) =
(p,q)∈P
i
(G
s
)
ROI(s, p,q) (9)
where P
i
(G
s
) is the set of all points in H
s
, V
s
and D
s
which constitute the connected subgraph CSG
i
(G
s
).
One can also see that by construction of the SOT the
ROI’s of two different points (s, p
1
,q
1
) and (s, p
2
,q
2
)
are disjoint, and hence so are the ROI’s of two differ-
ent connected subgraphs. Thus, the decomposition of
the graph G
s
to the mutually disjoint connected sub-
graphs enables us to define a set of mutually disjoint
domains on the image plane where the potential sur-
face features are located. Then, it is possible to calcu-
late the set of the initial guesses for the feature loca-
tion in order to initialize the optimization process.We

2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
(H) (V) (D)
Figure 4: One scale of HDT of the image on Fig. 3.
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
H
s
V
s
D
s
Figure 5: Binarization of the images displayed of Fig. 4.
use a rather simple strategy to establish the initial es-
timates for the surface parameters. Given the sets of
mutually disjoint connected subgraphs and their ROIs
we apply the following two-step heuristic decision:
S 1: Decide on the type of the feature (track/hole). For
example, number of vertices and types of edges of
CSG
i
(G
s
) could be used.
S 2: Given the ROI, try to compute the parameters of
a symmetrical feature of an appropriate type such
that it would fully occupy the ROI. See Fig. 8.
20 40 60 80 100 120
20
40
60
80
100
120
Figure 8: Image of the initial guess.
The only parameter which does not play any role in
this heuristic decision is the parameter h of the 2D
mesa-function. We suggest to overcome this prob-
lem by choosing the initial value of the parameter
according to the available data from the CAD of the
wafer. Let us also amplify the following advantage
of the proposed method. Since the ROIs are mutually
disjoint the optimization computations could be car-
ried out in parallel and his may provide considerable
speed-up in such a heavy computational task as SFS.
20 40 60 80 100 120
20
40
60
80
100
120
Figure 9: Lambertian image of the surface reconstructed by
our method from noise free image.

3.5.1 The Sfs Algorithm
We present the summary of our new SFS algorithm.
Input: 1. I(x,y) - input image.
2. S - the coarsest scale level of DHT.
3. LET - the local error tolerance.
Output: 1. Number of features found.
2. A vector of parameters of each feature.
3. A vector of local errors induced by the calcu-
lated vector of the parameters.
S 1: 1.1 Compute HDT of I(x,y) up to scale level
S.
1.2 Set the current scale level s = 1.
S 2: 2.1 Produce three binary images H, V and D at
the current scale s.
2.2 If the images H, B and D are zero - STOP.
S 3: 3.1 Build the connected components of H, V
and D.
3.2 Build the graph G
s
.
3.3 Compute {CSG
i
(G
s
)}
N
i=1
S 4: For each connected subgraph do
4.1 Decide on its type.
4.2 Calculate ROI(CSG
i
(G
s
)).
4.3 Calculate the initial estimate vector
~
α
0
.
4.4 Launch LM procedure on the ROI starting
with
~
α
0
, to determine
min
~
α
∑
(x,y)∈ROI
(I(x,y) − R(x,y;
~
α))
2
4.5 Save the resulting vector of parameters and
the error introduced by it.
4.6 If the error is less then the LET
4.6.1 For each pixel (p,q) ∈ P
i
(G
s
) set all
the wavelet coefficients in the SOT rooted at
(s, p, q) to zero.
4.6.2 Output the resulting vector and the er-
ror.
S 5: 5.1 Set s = s+1.
5.2 If s > S — STOP, otherwise GOTO Step
2.
It is worth mentioning LM scheme is one of the
most widely used non-linear data fitting methods, and
it is often described in the literature, see e.g. (Gill
et al., 1982).
4 RESULTS AND DISCUSSION
There are several important characteristics of the al-
gorithm which we shall subsequently point out.As we
build the DHT pyramid from the fine to the coarse
scale levels, the connected components of high ampli-
tude coefficients tend to mix together, meaning, that
the geometrical information carried by them is much
more precise on the fine levels of the pyramid. Actu-
ally, if the image is absolutely free of noise it is suffi-
cient to choose S = 1 to recover the surface. However,
in the presence of additive white noise the geometri-
cal information is likely to ”survive” at higher levels.
Note that if a feature has been recovered from some
coarse level s of the pyramid and some connected sub-
graph CSG
i
(G
s
), then there is no point in taking into
account the wavelet coefficients from finer levels be-
longing to the SOTs rooted at (p,q) ∈ P
i
(G
s
). That
is why the auxiliary step 4.6.1 has been introduced.
In order to demonstrate the efficiency and accuracy
of the proposed algorithm the SFS method based on
variationalapproachhas been implemented to provide
data for the performance comparisons. The images of
resulting surfaces are displayed on Figures 9 and 10,
when the image on Fig. 3 has been used as an input for
both methods. We also consider the case when the in-
put image is contaminated by additiveGaussian noise.
The advantage of using DHT from noise robustness
standpoint becomes obvious when one observes the
reconstruction using the binarized DHT of the noisy
input image displayed on Figure 11. Here we apply
Gaussian noise with mean = 0 and variance = 0.01.
One can see that in the presence of additive white
noise, no comprehensible information will be con-
tained at the finest level of the pyramid, see Figure 11
H
1
, V
1
and D
1
. On the other hand the information is
still available from the level corresponding to s = 3,
i.e. Figure 11 H
3
, V
3
and D
3
. Subsequently, the initial
estimation and the following minimization will not be
badly affected by the noise. The image of the sur-
face reconstructed from the noisy data is displayed on
Figure 12. Finally, error comparison between model
based and variational methods is given on Figure 13.
20 40 60 80 100 120
20
40
60
80
100
120
Figure 10: Lambertian image of the surface reconstructed
using variational approach from noise free image.

10 20 30 40 50 60
10
20
30
40
50
60
10 20 30 40 50 60
10
20
30
40
50
60
10 20 30 40 50 60
10
20
30
40
50
60
H
1
V
1
D
1
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
H
3
V
3
D
3
Figure 11: Binarization of the DHT of the noisy image.
20 40 60 80 100 120
20
40
60
80
100
120
Figure 12: Image of the surface reconstructed from noisy
data by our method.
Errors, STD
Method, Data type Brightness Depth
Our method, noise free 0.45 0.06
Our method, noisy 0.54 0.48
Variational method, noise free 2.73 2.12
Figure 13: Error comparison.
ACKNOWLEDGEMENTS
The generous support of Applied Materials Inc. is
thankfully acknowledged.
REFERENCES
A. Jones, G. T. (1994). Robust shape from shading. In
Image and Vision Computing, vol 12, no. 7. pp 411-
421.
Atick, J., Griffin, P., and Redlich, A. (1996). Statistical ap-
proach to shape from shading, reconstruction of three-
dimensional face surface from single two-dimensional
images. In Neural Computation 8, pp 1321-1340.
Gill, P., Murray, W., and Wright, M. (1982). Practical Op-
timization. Academic Press, London.
Horn, B. (1975). Obtaining shape from shading informa-
tion. In Psychology of Computer Vision. pp 115-155.
Horn, B. and Brooks., M. (1986). The variational approach
to shape from shading. In Computer Vision, Graphics
and Image Processing, vol 33, no. 1. pp 174-208.
Mallat, S. (1999). A Wavelet Tour of Signal Processing.
Academic Press, London, 2nd edition.
Prados, E., Faugeras, O., and Camilli, F. (2004). Shape from
shading: a well-posed problem ?. In INRIA, Tech. Re-
port. RR-5297.
R. Kimmel, K. Siddiqi, B. K. and Bruckstein., A. M. (1995).
Shape from shading: Level set propagatioin and vis-
cosity solutions. In International Journal of Computer
Vision, vol 16, no. 1. pp 107-133.
Reimer, L. (1993). Image Formation in Low-Voltage Scan-
ning Electron Microscopy. SPIE Press, Bellingham,
USA.
Shapiro., J. (1986). Embedding image coding using ze-
rotrees of wavelet coefficients. In IEEE Trans. on Sig-
nal Processing, vol 41, no. 12. pp 3445-3462.
T. Pong, R. H. and Shapiro., L. (1989). Shape from shading
using the facet model. In Pattern Recognition, vol 22,
no. 6. pp 683-695.
Zhang, R., Tsai, P., Cryer, J., and Shah., M. (1999). Shape
from shading: A survey. In IEEE Trans. PAMI Vol.21,
No. 8 pp 690-706.
Zheng, Q. and Chellappa, R. (1991). Estimation of illu-
minant direction, albedo and shape from shading. In
IEEE Trans. on PAMI, vol. 13, no. 7, pp 680-7021.
