MODIFIED DISTANCE SIGNATURE AS AN ENHANCIVE

DESCRIPTOR OF COMPLEX PLANAR SHAPES

Andrzej Florek and Tomasz Piascik

Institute of Control and Information Engineering, Poznan University of Technology, 60-965 Poznan, Poland

Keywords: Shape description, signature, object recognition, classification.

Abstract: In this paper, a simple and efficient approach to classify planar shapes is proposed. This approach is based

on comparison of areas of dynamicly sampled classic signatures. Presented approach is dedicated to the

recognition of convex and concave planar shapes, containing openings in the area enclosed by boundary.

A way to calculate the discrete representation of classic distance-versus-angle signatures, a reduction of

memory requirements and a number of calculations are presented. Analysis carried out from classification

experiments applied to images of real objects (car-engine collector seals) indicates good properties of

dissimilarity coefficients, based on modified signature, taken as an object descriptor.

1 INRODUCTION

The way of representing visual information

concerning the objects found in the scene plays

a fundamental role in the process of recognition and

classification. One of the most essential

characteristics enabling the recognition of an object

is a shape. That is why the analysis of the scene

often leads to the patterns comparison and to the

recognition of object shapes. The shape analysis is

linked with the problem of appropriate

representation of the shape and the methods of its

description (Demant, 1999), (Gonzales, 1992). The

methods of the shape describing are fundamentally

based on information concerning its contour or

information about its area as a whole. The object

description should be invariant with regard to

translation, rotation and scale change. Apart from

clarity, selectivity and precision, a good shape

descriptor should have low computation complexity

and universal application (Gonzales, 1992), (Zhang,

2004). The above-mentioned features of a good

descriptor are often contradictory.

In the following, the global approach towards the

shape description based on boundary by using

centroid distance signature is presented. The

modified principle of calcutating shape signature

and comparison with a standard approach is also

discussed. The algorithm efficiency of examining

the similarity both of convex and concave objects

and objects with openings is given. Application of

the modified signature in the process of recognition

is illustrated by classifying the images of car-engine

collector seals.

2 CENTROID DISTANCE

SIGNATURE AND ITS AREA

The classic shape signature is a 1D function

representing a 2D shape bordered by a contour. The

subject of discussion is the shape signature using the

distance of contour pixels from the defined reference

point. The standard example is the distance between

contour pixels and the center of gravity of the

contour (or whole figure) as the function of the angle

(Gonzales, 1992). This definition of the descriptor is

suitable for representing convex shapes. In many

concave or disconnected shapes (e.g. for objects

having holes), we obtain more than single distance

value for the same angle

. In a general case, the

signature is a mapping of the angle into a distance

set and the shape signature is represented by ordered

series of pairs S={(

, R

)}. To obtain R

values,

a continuous signature must be sampled. In a classic

approach, sampling is done at a constant step

Δφ

= 2

/N, where N is an assumed angular

resolution. As a result, sampled signature

representation S={(i

Δφ

, R

), i=1, ..., N} is obtained.

225

Florek A. and Piascik T. (2007).

MODIFIED DISTANCE SIGNATURE AS AN ENHANCIVE DESCRIPTOR OF COMPLEX PLANAR SHAPES.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 225-230

 SciTePress

In a general case, more R

for a given i

Δφ

obtained (Parker, 1998).

The approach proposed here consists of tracking

the contour pixel by pixel and building a signature

taking into account the local dynamics of the

contour. With this approach sampling is performed

at a variable step. The algorithm of shape signature

determination consists of the following steps:

1. Extracting all object contours.

2. Calculating coordinates of a chosen reference

point P

, y

3. Tracking an external contour C.

4. For each pixel C

, y

), calculating a distance

from the point P

and an angle

as arctan(( y

– y

)/(x

– x

)) and storing them

in a signature mapping table S[

, R

5. Determining a maximal distance R

MAX

6. Rewriting chosen normalized values R

MAX

to a modified signature table.

7. Repeating the whole procedure for all internal

contours of openings in the analyzed object

(steps 4-6).

The choice of consecutive points from the

signature mapping table S[

, R

], to rewrite them

into the modified signature table, is determined by

three parameters, which describe sampling process:



R/R − the relative pixel distance change

parameter between consecutive signature

points (the fundamental sampling condition

meaning that for consecutive point

j+1

−

/ R

MAX

≥

R/R );



MIN

− the minimal angle change between

signature samples (a condition guaranteeing

that between consecutive modified signature

points the angle increment will not be less

then a predefined value

j+1

≥

MIN

);



MAX

− the maximal angle change (the angle

increment will not be greater then a predefined

value

i+1

≤

MAX

This process determines a modified signature

taking into account the dynamics of the shape. For

R/R = 0 classic shape signature is obtained for step

Δφ

MIN

. The choice of the reference point P

should not be accidental to ensure the invariance

with regard to the object translation in the frame.

The less subject to disruption the location of P

, the

more precise the descriptor. The normalization with

respect to R

MAX

lets the descriptor to be invariant

regards to the scale change.

In the presented approach, the essential element

for signature comparison is the signature area. In the

case of some convex shapes, the signature area

corresponds to the area delimited by a curve built of

signature points. In the case of some concave objects

and objects with openings, in order to determine the

signature area, there is a need for interpolation of the

modified signature. This is a consequence of the

variable sampling rate and the independent external

and internal contours tracking. After extending the

modified signature to each spike, the appropriate

region filling is made (Fig. 1). At this stage, the

information from contour tracking algorithm is used.

3 SIMILARITY OF PLANAR

OBJECTS

Object similarity analysis, while signatures represent

shapes, refers to the comparison of signature areas

(Parker, 1998). For comparison the XOR operation

between the spikes of two signatures is used.

Comparison is made with respect to the

corresponding values of scanned angles. The

calculated difference between areas is related to the

reference area and this relative symmetric area

difference is taken as a coefficient of non-similarity

of compared shapes (DISS coefficient). As the

reference area, an area of the box bounding signature

or an area of one of the compared signatures is

taken. To suppress nonlinear effects, due to the

transformation from the Cartesian coordinate system

to the polar coordinate system, R

MAX

values in

XOR operation are used, while calculating signature

area. In this way, weight coefficient of an area pixel

is proportional to the pixel distance from the

reference point, as every area pixel represents the arc

length of circle section determined by

MIN

and R

Such a coefficient is denoted as DISSW.

Rotational invariance is obtained by repeated

calculations of signature area differences, each time

cyclically translating one signature with respect to

the other. The minimum of calculated XOR values

(i.e. XOR value for the best matching of shape

signatures) determines the DISSW coefficient value

(3). With the classic approach, both signatures have

N spikes, for the same angle values. In the proposed

approach, modified signatures consist respectively

of N

≤

N and N

≤

N spikes. In the case of classic

signatures, N

comparisons are required (for N area

spikes and N shifts). In the proposed modification

case, only N

comparisons are performed, because

the second signature is shifted only N

times and

compared for N

angle values. Spikes are not

available for all angle values, thus to calculate XOR

area difference an interpolation has to be performed.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

226

4 EXPERIMENT DESCRIPTION

In order to validate the proposed approach to the

objects classification an experiment consisting of

examining a set of car-engine seals was undertaken.

In the experiment twelve seals (twelve classes of

objects) were used, for which twenty shots in several

varied positions were made (for various orientations

and projection scales). The scene was lit by two

lamps from above obliquely from two opposites

sides thus object edges cast slight shadows. After

preprocessing, tresholding and filtration with

a median filter 3×3, a set of 240 binary images of

objects was created (resolution 2 pixels/mm). The

first shot in each population for each class,

maintaining the same stable acquisition conditions,

produced image of class prototype. These prototypes

for twelve classes are shown in Fig. 2.

Comparison of classification methods using

classic and modified signatures was based on DISSW

value histograms comparison. Changes of class

discrimination measure, based on DISSW mean and

standard deviation values were analyzed.

4.1 Parameters of Analysis

For analyzed images, classic signature was

calculated for

Δφ

= 0.5°. For calculating modified

signature values

R/R ≤ 2.5% and

MAX

= 5° have

been chosen. These parameters enable still

appropriate reconstruction of object contours.

Values of DISSW errors were calculated for all

prototypes of classes by using classic signature

comparison method. After analyzing these results,

two seal pairs with the smallest dissimilarity errors

were chosen. Comparison of classifiers based on

classic and modified signatures was executed for

pairs (H2, H4) and (D3, N2). Dissimilarity errors

were calculated for each image compared to the

others. If for ordered pair of classes (C1, C2) the sets

of their signatures are denoted as:

SC1 = {sc1

, sc1

, ..., sc1

}, (1)

SC2 = {sc2

, sc2

, ..., sc2

} (2)

where sck

is the signature for i

image of the object

from Ck, then the dissimilarity errors for a pair

(C1, C2) are calculated for all i, j

∈ {

1, 2, ..., 20} as:

DISSW = min [( sc1

)

XOR(sc2

)] / sc1

(3)

First, errors in the standard case for

Δφ

= 0.5°

(N = 720) were calculated. Then, resolution was

decreased to

Δφ

= 1.5° (N = 240). These results are

compared to the errors obtained with the modified

signature, at

⎯

MOD

≈

N. Modified signatures were

calculated for:

MIN

= 0.5°,

MAX

= 5°,

R/R = 2%.

Experiment was performed for two reference points

(center of shape and center of boundary).

The calculated DISSW values are distorted by:

a transformation to the polar coordinate system,

a discretization, a tresholding (all being a method

error) as well as by optical deformations of camera

and shadows on the scene. The method error was

checked for standard case at

Δφ

= 0.5° with the

center of shape as the reference point. DISSW values

were calculated for prototype images analytically

transformed to positions corresponding to object

positions in the set of images for a given class.

These errors did not exceed 5%. The remaining

errors are regarded as a noise.

4.2 Analysis of Results

Analysis of experimental results is based on

comparison of mean and standard deviation values

(m,

)

for within-class and between-class errors. In

Fig. 3, DISSW coefficient values histograms for pair

(H4, H2) are presented. In the standard case for

shape center and for

Δφ

= 0.5° (named as an

accurate case), calculated values of statistical

parameters (m,

σ)

of DISSW values are as follows:

 ( 6.0, 2.3) for (H2, H2);

 (28.0, 1.4) for (H2, H4);

 ( 6.1, 2.4) for (H4, H4);

 (26.9, 1.5) for (H4, H2).

To compare both classic and modified methods,

a dispersion measure of classes (C1, C2)

is defined

as:

D (C1,C2) = |m

C11

− m

C12

C11

C12

)

− 0.5

(4)

where m

C11

are the mean and the variance of

(C1, C1) within-class DISSW values and m

C12

are the mean and the variance of (C1, C2) between-

class DISSW values, respectively.

Calculated values of D are presented in Tab. 1.

In the standard case (

Δφ

= 1.5°), for pairs (H2, H4)

and (H4, H2), value of the measure D decreases,

nearly twice. In the modified signatures case, at the

same number of signature spikes, value of the

dispersion measure D increases with respect to

standard case (

Δφ

= 1.5°) and is even bigger then in

the accurate case (

Δφ

= 0.5°). The results for the

pair (D3, N2) change in a similar manner.

MODIFIED DISTANCE SIGNATURE AS AN ENHANCIVE DESCRIPTOR OF COMPLEX PLANAR SHAPES

227

Table 1: Values of dispersion D for center of shape.

Method H2 H4 H4 H2 D3 N2 N2 D3

Classic

Δφ

= 0.5° 8.1 7.4 9.0 9.8

Classic

Δφ

= 1.5° 4.5 3.8 7.3 7.8

Modified 8.5 8.0 9.0 9.9

Table 2: Values of dispersion D for center of boundary.

Method H2 H4 H4 H2

Classic

Δφ

= 1.5° 2.1 2.4

Modified 2.9 4.2

Greater values of D and their smaller changes are

due to other type of shape and reduced radial

resolution. Applied radial resolution was always

equal to 1/500 R

MAX

, but objects from D3 and N2

classes have bigger absolute values R

MAX

then the

other ones.

Finally, results for modified and standard case

(

Δφ

= 1.5°) are compared while the reference point

was changed. Results for pair (H2, H4), calculated

for center of external contour as the reference point,

are presented in Fig. 4 and Tab. 2. Increase of error

values and their standard deviation values can be

observed. For standard case, (m,

) values of

DISSW coefficient are as follows:

 (12.6, 5.7) for (H2, H2);

 (27.0, 3.8) for (H2, H4);

 (11.7, 4.7) for (H4, H4);

 (25.9, 3.7) for (H4, H2).

Figure 1: Shape of a car-engine collector seal (left) and its modified signature (right).

Figure 2: Images of car engine collector seal class prototypes.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

228

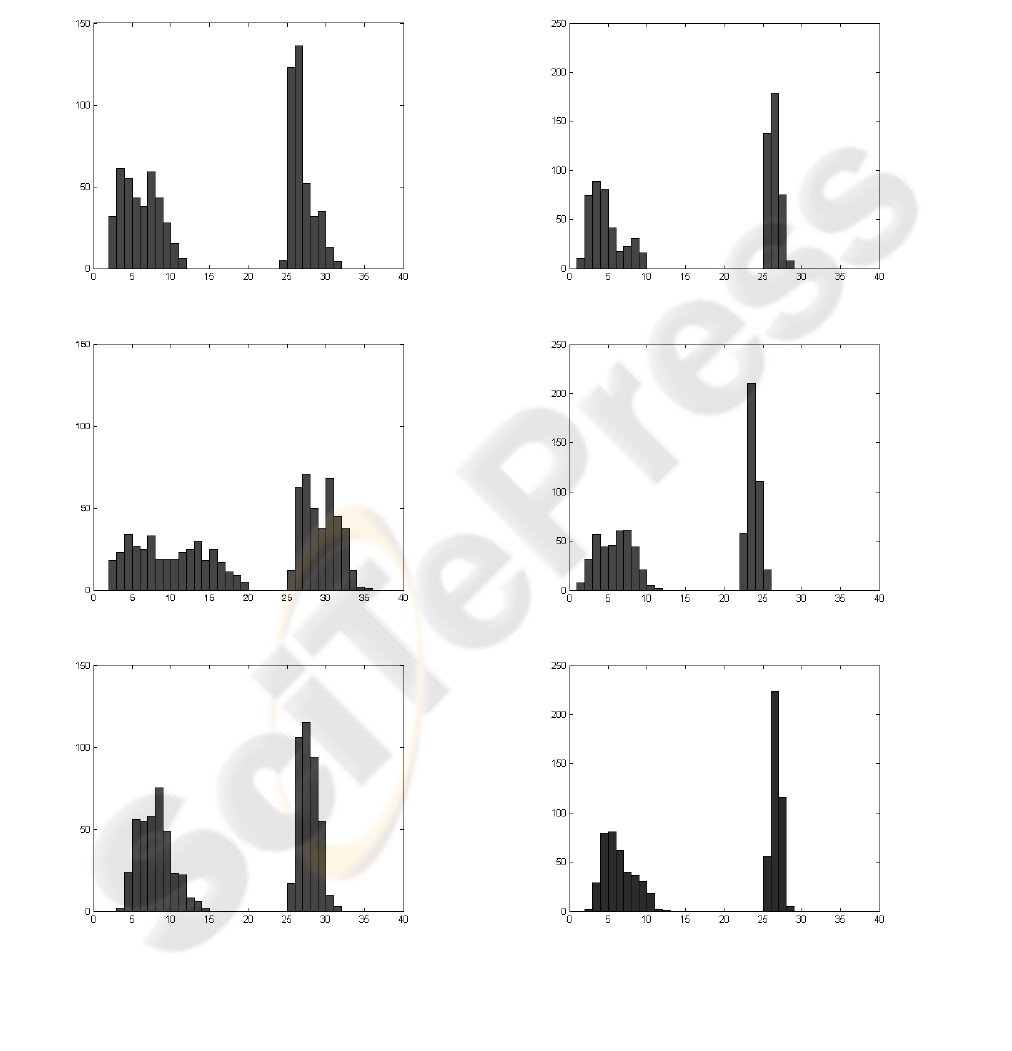
This is due to the greater sensitivity of contour

center to the noise. For considered objects, the

number of contour pixels was 30 - 40 times smaller

that the number of pixels belonging to the object

shape. Decrease of angular resolution and increase

of noise level lead to overlapping between within-

class and between-class errors (in Fig. 4 common

area of histograms is marked by light gray color).

The modified signature improves the

discernability of classes. Tests performed on

modified signatures of real images reveal good

properties of the dissimilarity coefficient as an

object discriminator.

Figure 3: Histograms of within-class and between-class dissimilarity errors for (H4, H2) – left and (N2, D3) – right,

for shape center as the reference point: a) classic Δφ = 0.5°, b) classic Δφ = 1.5°, c) modified

ΔR/R = 2%,⎯N

= 250,⎯N

= 237.

MODIFIED DISTANCE SIGNATURE AS AN ENHANCIVE DESCRIPTOR OF COMPLEX PLANAR SHAPES

229

Figure 5: Histograms of within-class and between-class dissimilarity errors for (H2, H4) – left and (H4, H2) – right, for

boundary pixels center as the reference point: a) classic Δφ = 1.5°, b) modified ΔR/R

MAX

= 2%,⎯N

= 242, ⎯N

= 253.

5 SUMMARY

Application of the signatures of planar objects to

recognition and classification is simple, fast and

computationally effective. The presented method

of describing complex objects can be used in the

case of convex, concave and disconnected shapes

with openings. The modified shape descriptor is

invariant to translation and scale change, and the

mode of comparison assures its invariance with

regard to rotation. The proposed modified

approach takes into account the variability of

object contours leading to automatic changes in the

frequency of sampling of classic signatures. The

descriptor is directly connected with the shape of

the object. Parameter values taken to calculation of

the modified signature are simple to choose and the

validation of shape comparison results is natural.

The use of modified signatures reduces the

memory requirements and the number of

calculations without deteriorating recognition

results. Test undertaken on the real objects images,

indicates a good performance of the dissimilarity

coefficient determined with the modified signature

method. This coefficient enables good

discrimination of objects indicating the suitability

of this method for robotic inspection and visual

control systems.

REFERENCES

Demant, C., Streicher-Abel, B., Waszkiewitz, P., 1999.

Industrial Image Processing. Visual Quality Control

in Manufacturing, Springer Verlag, Heidelberg.

Gonzales, R.C., Woods, R.E., 1992. Digital Image

Processing, Addison-Wesley, Reading MA.

Parker, J.R., Zhang, Z., 1998. Object recognition using

signatures, Proc. IASTED Int. Conf. Signal and

Image Processing, Las Vegas, pp. 1-5.

Zhang, D., Lu G., 2004. Review of shape representation

and description techniques, Pattern Recognition 37

(1), pp. 1-19.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

230