
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT
AREAS AND PROPOSAL FOR A LOW-COST
IMPLEMENTATION
1,2
Frederique Crete,
1
Marina Nicolas
1
STMicorelectronics,12 rue Jules Horowitz, 38019 Grenoble, France
2
Patricia Ladret
2
Laboratoire des Images et des Signaux, 46 Avenue Félix Viallet, 38031 Grenoble, France
Keywords: Deblocking, flat areas, grey level gradation, low-cost, objective metrics.
Abstract: The quantization of data from individual block-based Discrete Cosine Transform generates the blocking
effect estimated as the most annoying compression artefact. It appears as an artificial structure caused by
noticeable changes in pixel values along the block boundaries. Due to the masking effect, the blocking
artefact is more annoying in flat areas than in textured or detailed areas. Existing low-cost algorithms
propose strong low-pass filters to correct this artefact in flat areas. Nevertheless, they are confronted to a
limitation based on their filter length. This limitation can introduce other artefacts such as ghost boundaries.
We propose a new principle to detect and correct the boundaries on flat areas without being limited to a fix
number of pixels. This principle can be easily implemented in a low-cost post processing algorithm and
completed with other corrections for perceptible boundaries on non-flat areas. This new method produces
results which are perceived as more pleasing for the human eye than the other traditional low-cost methods.
1 INTRODUCTION
The quantization of data from individual block-
based Discrete Cosine Transform generates the
blocking effect estimated as the most annoying
compression artefact. The blocking artefact appears
as an artificial structure caused by noticeable
changes in pixel values along the block boundaries.
Sometimes masked by textured areas, the block
boundaries are particularly detected by the human
eye on homogeneous or flat areas.
The blocking effect is well known and lots of
corrections have been proposed. Among them,
methods based on wavelet representation (Gopinath,
1994), on the Markov random fields, or on
projection on convex set (Yang, 1995), need high
computation time and memory. For real-time videos
processing, methods such as adaptive filters are
more suitable. However, some of these methods are
limited because they need to know the DCT
coefficients (Chou, 1998) or the information coming
from the decoder such as the quantization parameter
(List, 2003). To cover the largest possible domain,
we target our study to a post-processing deblocking
with the pixels value as the only aFvailable input
data. In this case of post-processing real-time
corrections, possibilities are limited and existing
algorithms are generally divided into two steps
(Kuo, 1995): a first step to localize the perceptible
boundaries and a second step to suppress these
boundaries. The detection step is made by an
analysis of the pixels values on both sides of the
boundaries. Then, according to this local pixel
information around the block boundary, an adaptive
filter is chosen for the correction step.
Unfortunately, this kind of correction has a
limitation due to the risk of overlapping between
input data to be corrected in current block and
already corrected data from previous block. Figure 1
illustrates this phenomenon and shows that the
number of pixels used to process the detection and
the correction step is limited to the half length of a
block. For example, to correct the boundary B
n+1
, we
need to analyse the block Blk
n+1
which can has been
32
Crete F., Nicolas M. and Ladret P. (2007).
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT AREAS AND PROPOSAL FOR A LOW-COST IMPLEMENTATION.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 32-39
Copyright
c
SciTePress
modified during the correction of the boundary B
n
.
By using the half length of the block, existing
algorithms avoid the phenomenon of overlapping
between two consecutive processes.
Figure 1: Traditional method to process a boundary.
After compression, flat areas are represented by
several homogeneous blocks. For a perceptible
boundary between two homogeneous blocks, the
major consequence of the limitation described above
is the apparition of two ghost boundaries on both
side of the initial boundary at the start and the end
positions of the correction. Figure 2 illustrates this
problem. Even if these ghost boundaries are less
perceptible than the initial one, they remain an
artificial structure which is annoying for the eye.
Averbuch et al (2005) propose to solve the problem
of ghost effect in flat areas using an iterative
principle based on varying size filters but still
limited to a size of eight. Even if this method has a
good performance, we focus our study on a non-
iterative and more simple method based on a simple
observation: the ghost boundaries disappear if the
correction is done on all pixels of the blocks.
Figure 2: The ghost boundaries G
n_L
and G
n_R
after
filtering the initial boundary B
n
.
In case of high compression rates, data are so
compressed that pixels value of homogenous blocks
converge to the same one. Consequently, in flat
areas, homogeneous blocks merge and form a larger
uniform block without intermediate boundaries.
Figure 3 shows that for high compression rates, there
are less boundaries but they are more perceptible. If
the boundaries are more perceptible, we can imagine
that the ghost boundaries made by a correction on a
fixed number of pixels will be highly perceptible
and very annoying for the eye. This phenomenon of
block merging has already been taken into account
(Pan, 2004) to refine quality metrics for high
compression rates. In the same way, if we localize
invisible boundaries caused by the block merging,
we will have more pixels available and we could
apply a stronger correction in order to avoid the
ghost boundaries apparition.
Figure 3: On the left, compression at 0.6 bbp, on the right,
compression at 0.4 bpp: for high compression, they are
less boundaries but highly perceptible.
By using the maximum number of pixels available
to correct a perceptible boundary, we propose a new
solution to remove the blocking artefacts on flat
areas without creating ghost boundaries.
In section 2, we explain our methods a) to
detect boundaries between two homogenous blocks,
b) to find invisible boundaries caused by the block
merging phenomenon and c) to explain the ideal
adaptive filter to correct these boundaries. In section
3, we describe how to implement these methods in a
low-cost algorithm by taking into account the
phenomenon of overlapping. Section 4 illustrates the
improvements on experimental results. Section 5
provides the conclusion of this paper.
2 METHODS TO DETECT AND
CORRECT THE BLOCKING
ARTEFACT ON FLAT AREAS
We consider the case of boundaries localized on a
regular 8x8 grid because digital video compression
algorithms like MPEG-1, MPEG-2 or H263 use a
size of block of 8x8 pixels. Our principle could be
easily adapted for a size of blocks of 8*4 or 4*4
pixels for compression algorithms like MPEG4 or
H264 but in the case of a shift grid due to a resizing,
a step to detect the boundaries position would be
necessary. We illustrate our purposes only on the
vertical boundaries but the principle is the same for
the horizontal boundaries.
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT AREAS AND PROPOSAL FOR A LOW-COST
IMPLEMENTATION
33
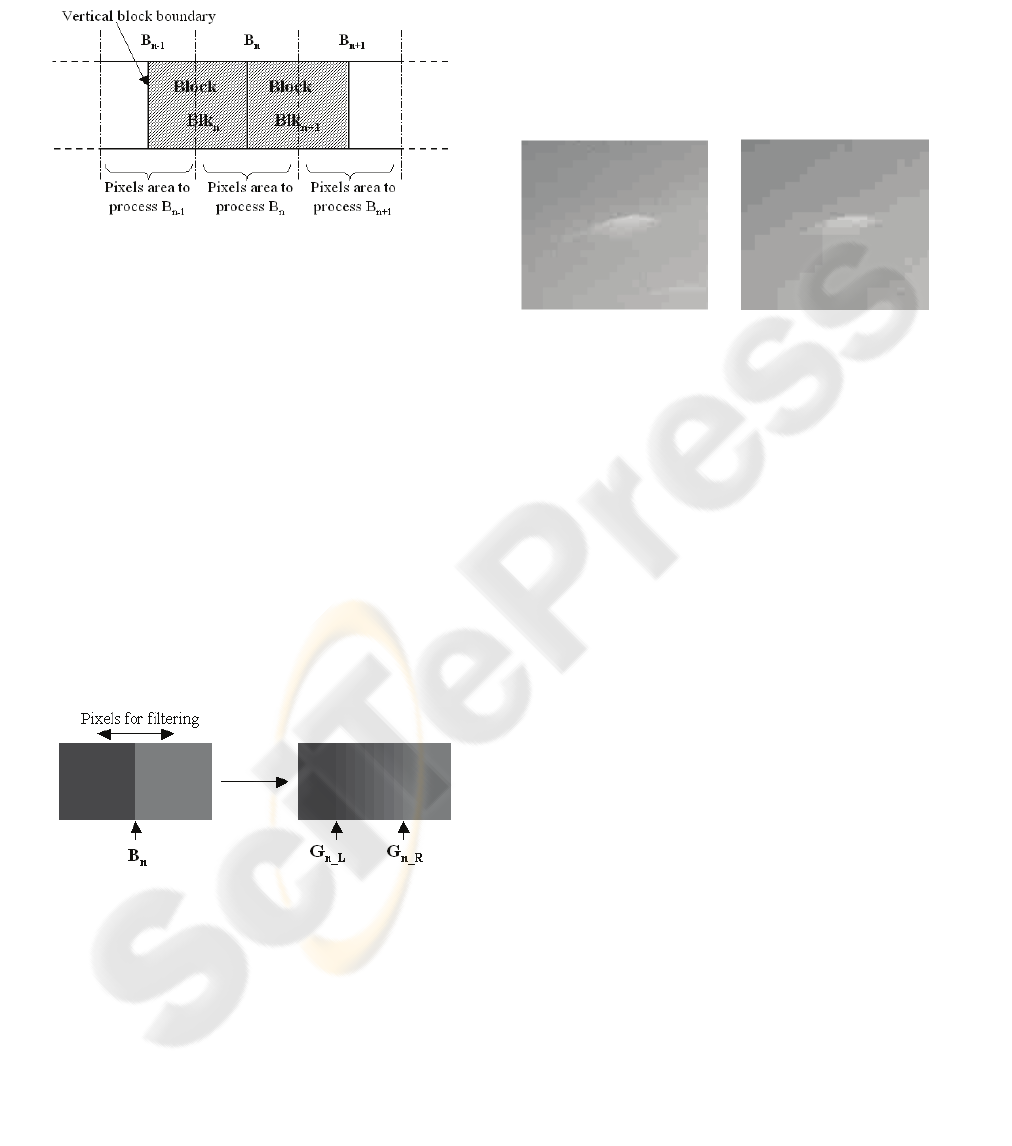
2.1 Detection of Boundaries between
Two Homogeneous Blocks
To detect a boundary between two homogenous
blocks, we analyse the content of the blocks areas on
both side of the boundary. Figure 4 illustrates the
detection steps.
Figure 4: Detection of a boundary between two
homogeneous blocks.
1
st
step: On each line of the array f which represents
a pair of blocks, we make the absolute difference
abs_diff between neighbouring pixels to distinguish
flat from textured areas.
2
nd
step: Then, by summing up the results over the
lines for each column, we are able to analyze the
global visibility of the boundary between two
blocks.
The left area is a homogeneous block if:
∑
=
==
6
0
0)(
j
jresLeftArea
(1)
The right area is a homogeneous block if:
∑
=
==
14
8
0)(
j
jresRightArea
(2)
The boundary is perceptible if:
TresholdresBound <=< )7(0
(3)
Over a range, the boundary is too perceptible to be
an artefact compression that is why the threshold is
used to not confuse the block boundaries with the
edges of the image content.
Finally, a boundary is defined as a perceptible one
between two homogeneous blocks if:
0=LeftArea
0=RightArea
TresholdBound<<0
(4)
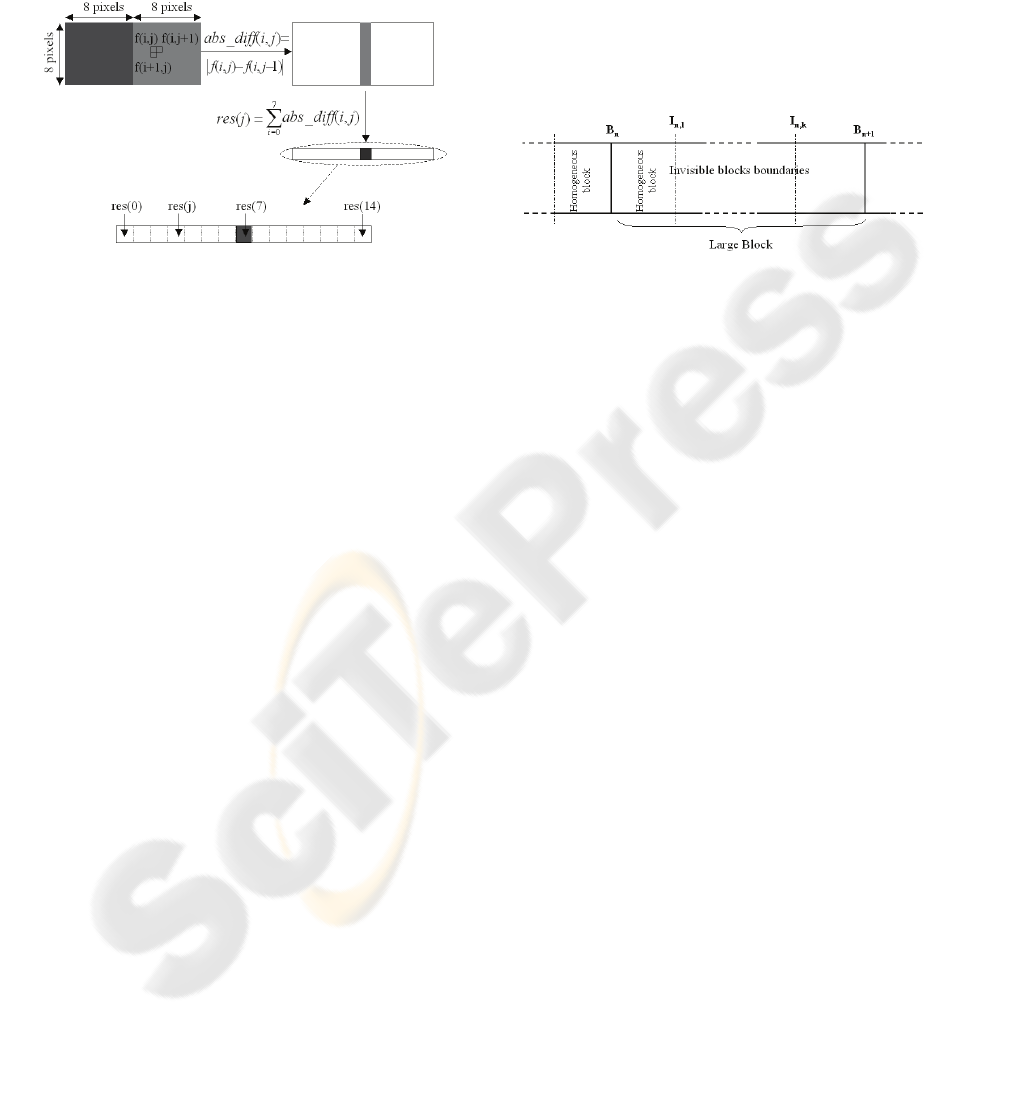
2.2 Detection of Invisible Boundaries
Due to the Merging Block
Phenomenon
As we explain in the introduction, the large block
phenomenon is the result of a high compression:
neighbouring blocks merge and intermediate
boundaries become invisible. Consequently, the
major challenge to detect the large blocks without
intermediate boundaries consists in not confusing
them with the homogeneous regions of the initial
frame. To be considered as an invisible boundary
due to the merging blocks phenomenon, this
boundary must be in a highly compressed region.
Consequently, we define a large block (Figure 5) as
one or several invisible boundaries I
n,k
following a
perceptible boundary B
n
between two homogeneous
blocks.
Figure 5: The large block definition.
To detect an invisible boundary between two
homogeneous blocks, we use the same analysis as
the previous section (See Figure 4). We declare a
boundary invisible between two homogeneous
blocks if:
0
=
LeftArea
0
=
RightArea
0
=
Bound
(5)
Then, we declare that the invisible boundaries I
n,k
result from the block merging if:
B
n
is a perceptible boundary between two
homogeneous blocks
I
n,1
…. I
n,k
are invisible boundaries
(6)
2.3 Correction of Boundaries between
two Homogeneous Blocks
A boundary between two homogeneous blocks is
perceptible because the grey level g
left
of the left
block and the grey level g
right
of the right block are
different. Existing corrections are limited because
the absolute difference between g
left
and g
right
could
be so high that a filter on eight pixels is not
sufficient and can introduce ghost boundaries.
We propose a correction which consists in spreading
the gradation defined by the absolute difference
between g
left
and g
right
on the maximum number of
available pixels. This correction is introduced by the
equation (7) where f
corr
(i,j) is the correction of each
pixel (i,j) of the two adjacent blocks, S
B
is the size of
available pixels (16 in case of blocks of 8*8 pixels)
and g
left
and g
right
are the respective grey levels of the
left and the right blocks.
for j=0 to (S
B
-1) and for i=0 to 7:
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
34

)1(
))1((
),(
−
×+×−−
=
B
rightleftB
corr
S
gjgjS
jif
(7)
Figure 6 shows the result obtained by using a) a
correction limited on a fixed number of pixels and b)
our correction. We observe that ghost boundaries
G
n,L
and G
n,R
have disappeared and the gradation
between g
left
and g
right
is better
spread.
Figure 6: Correction of a boundary using a) method
limited on the half length of a block b) method using the
entire blocks.
2.4 Correction of Boundaries Using the
Large Block Detection
The more the compression rate increases, the more
the absolute difference between g
left
and g
right
is high
and the more we need available pixels to spread the
gradation. By detecting the invisible boundaries
following a perceptible boundary (the block merging
phenomenon), we dispose to more available pixels
to spread the correction. The process until now
limited to 16 pixels can be extended to a number of
pixels proportional to the number of invisible
boundaries. The correction is traduced in the
equation (8) where S
LB
is the size of the large block.
for j=0 to (S
LB
-1) and for i=0 to 7:
)1(
))1((
),(
−
×+×
−
−
=
LB
rightleftLB
corr
S
gjgjS
jif
(8)
Figure 7 shows the real improvement of the correction
when we use all available pixels compared to the
corrections limited to a fixed number of pixels.
Figure 7: Correction of a boundary using traditional
method limited on the half length of a block and our
method filtering on all available pixels.
3 PROPOSAL FOR A LOW-COST
IMPLEMENTATION
We propose in this section to include our methods
of detection and correction in a low-cost algorithm
able to take into account the overlapping
phenomenon. Figure 8 illustrates the steps presented
in the subsections 3.1 and 3.2.
3.1 Avoid the Overlapping Problem for
the Boundaries Detection
We consider Blk
n
as the left block, Blk
n+1
as the right
block and B
n
the boundary between Blk
n
and Blk
n+1
.
We suppose that the boundary B
n
is a perceptible
one between the two homogeneous blocks Blk
n
and
Blk
n+1
(Figure 8a). In this case, we apply a correction
on all available pixels using the equation (7). We
obtain the two corrected blocks Blk
n
and Blk
n+1
(Figure 8b). Moreover, we indicate into a flag that
the corrected boundary B
n
was a perceptible one
between two homogeneous blocks. To correct the
next boundary, the algorithm makes a switch of one
block. In this way, the algorithm studies the
boundary B
n+1
between the block Blk
n+1
and the
block Blk
n+2
(Figure 8c). If Blk
n+2
is an homogenous
block, we look for the flag. If the flag indicates that
the last correction was between two homogeneous
blocks, we know that before the last correction,
Blk
n+1
was homogenous. So, we have to consider
Blk
n+1
and Blk
n+2
as two homogeneous blocks. The
next step consists in computing the visibility of the
boundary so we have to compute the variable Bound
(3). Bound is the result of the absolute difference
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT AREAS AND PROPOSAL FOR A LOW-COST
IMPLEMENTATION
35

between the last column of Blk
n+1
and the first
column of Blk
n+2
. Even if the pixels of the block
Blk
n+1
have been modified during the last correction,
our correction has not changed the last column of
Blk
n+1
:
Before the correction:
rightn giBlk =+ )7,(1
By applying the equation (7), we obtain the
correction:
right
rightleft
corrn g
gg
ifiBlk =
×+×
==+
15
150
)15,()7,(
1
The compute of Bound is not biased by the
correction made on the 16 pixels.
The value of Bound reveals now if the boundary
B
n+1
is perceptible or not.
3.2 Avoid the Overlapping Problem for
the Boundaries Correction
To continue the previous example, we will see how
we take into account the overlapping problem for the
correction step.
3.2.1 The Boundary B
n+1
is Perceptible
If B
n+1
is detecting as a perceptible boundary
between two homogenous blocks (4), we apply the
equation (7) to spread the gradation between the new
g
left
and g
right
(Figure 8d).
But we have to slightly modify the equation to be
sure to represent all grey levels of the initial blocks.
In fact, if g
left
<g
middle
<g
right
or g
left
>g
middle
>g
right
, there
is no problem because to spread the gradation
between g
left
and g
right
, we meet g
middle
. But if
g
left
<g
middle
>g
right
or g
left
>g
middle
<g
right
, g
middle
would be
not represented.
Figure 8: Successive corrections of perceptible boundaries
between homogeneous blocks.
Consequently, we modify the equation by adding the
intermediate grey level g
middle
:
for i=0 to 7:
If g
left ≠
g
middle
or g
middle ≠
g
right
(9)
for j=0 to S
B
/2-1
12
))12((
),(
−
×+
×
−
−
=
B
middleleftB
corr
S
gjgjS
jif
for j=0 to S
B
/2-1
12
))12(
),(
−
×+
×
−
−
=
B
rightmiddleB
corr
S
gjgjS
jif
else
for j=0 to S
B
-1
)1(
))1((
),(
−
×+
×
−
−
=
B
rightleftB
corr
S
gjgjS
jif
end
Figure 9 illustrates the two cases corrected with
a)methods limited on a fixed number of pixels and
b)our method. We observe that our method does not
introduced ghost boundaries and make a better
gradation of all grey levels.
Figure 9: Correction of successive boundaries using a)
method limited on the half length of a block b) method
using the entire blocks.
3.2.2 The Boundary B
n+1
is Invisible
We suppose now that B
n+1
is detected as an invisible
boundary between two homogenous blocks (5). To
be conform with our definition of a large block
(Figure 5), we have to look at the type of the
previous boundary to decide of the next step. If the
flag is equal to 0, it means that the previous
boundary was not between two homogenous blocks.
The flag stays at 0 and there is no correction. On the
contrary, if the flag is equal to 1, we understand that
the last boundary was a perceptible one between two
homogeneous blocks. In this case, we define B
n+1
as
the first invisible boundary I
n,1
of a large block
(Figure 10). We apply the correction of the equation
(7 or 9) to spread the gradation between g
left
and
g
right
.
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
36

Figure 10: Large Block correction using a) method limited
on the half length of a block b) our principle in a low-cost
algorithm c) our principle.
This correction (Figure 10b) is slightly less
performed than the correction proposed in section
2.4 represented on Figure 10c. But we propose a
low-cost algorithm which make a one pass
processing on each pair of blocks. To apply the ideal
correction (section 2.4), we have to compute the
number of invisible boundaries and then to apply the
correction: this is impossible for a one pass
algorithm.
3.3 The Large Block Size
The threshold referred in the equation (3) of the
subsection 2.1 is used to distinguish an edge from a
block boundary. After several tests, we limited it to a
difference near from 24 grey levels. For this reason,
we estimate that a size of three blocks (24 pixels in
our case) is sufficient to make a good correction
without introduce ghost boundaries for a large block
correction. In this way, flag=0 after an invisible
boundary detection. Nevertheless, this number can
become insufficient for future implementation where
more than 8 bits would be used for the coding of the
pixel component values. In this case, the detection of
more than one invisible boundary can be useful.
3.4 Horizontal Boundaries and
Chrominance Component
In order to propose a low-cost algorithm, we do not
apply the large block correction for horizontal
boundaries. It is a means to avoid a complex control
of another variable flag for horizontal boundaries.
This limitation has not major consequences because
the large block is detected in most of cases on
homogeneous areas such as sky or sea where the
light has a tendency to be horizontally diffused.
In the same way, this kind of landscape has one hue
and variations are represented with the luminance
gradation. Consequently, the large block correction
is not necessary for the chrominance component.
3.5 Flow Chart of the Algorithm
To summarize those steps, we propose the flow chart
of this algorithm (Figure 11) with the sections and
the equations references. Moreover, we add in this
algorithm the possibility to combine other
corrections corresponding to perceptible boundaries
between textured or containing edges areas.
Figure 11: Flow Chart of the algorithm.
4 RESULTS
We propose to compare the results of “traditional
methods” which are low-cost algorithms based on a
fix number of pixels to “our method” which use all
available pixels. To represent the traditional
methods, we apply the same filter of our method but
only on four pixels on each side of the boundary.
This test is made for pictures with more or less flat
areas at different compression rates.
4.1 Visual Results
On Figure 12, we show from left to right the
uncompressed pictures, the compressed pictures,
pictures corrected with traditional method and
pictures corrected with our method. For the first
picture A1, the blocking artefact is very annoying.
Traditional methods correct the block boundaries but
we perceive again a blocking artificial structure due
to the ghost boundaries. Our method proposes a
correction perceived as more pleasing because it
does not introduce any new artificial block structure.
For the same picture A2 which is less compressed,
we have the same quality of results as the traditional
methods. We note for this picture that the initial
blocking artefact was not very annoying. For the
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT AREAS AND PROPOSAL FOR A LOW-COST
IMPLEMENTATION
37

third picture B, we note the real improvement given
by our method. This picture has a large flat area that
is why our principle of correction is very suitable
(the correction would be better if we apply the
correction in the ideal case as we explain at the end
of the subsection 3.2.2). Then, the last picture C is
highly compressed but on small flat areas.
Consequently, the blocking artefact appears less
perceptible than on A1 or on B. We note that our
method is slightly better compared to traditional
methods, since the artificial structure of corrected
boundaries does not appear.
4.2 Objective Metrics
We analyse the results of our method with two
objective metrics. First, we use the traditional
PSNR. As the PSNR is a reference metric, we
compare the compressed and the two corrected
pictures to the original uncompressed picture.
Table1: PSNR resluts (dB).
Image Compressed
Traditional
Method
Our Method
A1 19,34 19,58 19,56
A2 19,34 21,11 21,12
B 20,17 20,28 20,28
C 24,09 24,47 24,46
Table 1 shows the benefit of the corrections with the
increase in PSNR values. Nevertheless, the PSNR
does not distinguish the two methods in term of
quality. This limitation is explained by the fact that
the PSNR is an algebraic measure for the quality of
the reconstruction of an image. In our case, a lot of
information has been lost during the compression
step and we try to obtain the reconstruction the more
pleasing for the human perception. In our case, the
PSNR is thus not well adapted.
Then, we confront the methods by using a no-
reference metric only focusing on the block
boundary visibility (Wang, 2002). This metric
ranges from 0 to 10 which are respectively the worst
and the best quality. As for the PSNR, the benefits
of the corrections appear in the results but this
metric does not distinguish the two methods either
(Table 2). We may infer that the Pan metric (Pan,
2004), which may be better adapted to our situation
thanks to its large block consideration, would give
scores for the compressed pictures that are better
correlated with the human perception. But this
metric will not distinguish the two methods either. In
fact, these methods measure the visibility of the
boundary on the initial grid position (every 8*8
pixels in most cases) that is why they are not able to
distinguish the improvement of our method. To give
an objective score of the visual improvement, we
have to use a metric able to localize all artificial
structures included the ghost boundaries.
Table 2: Wang metric results.
Image Original Compressed
Traditional
Method
Our
Method
A1 9,89
5,11 7,26 7,39
A2 9,89
7,82 8,32 8,38
B 9,67
5,14 7,54 7,59
C 10,13
4,48 8,11 8,21
5 CONCLUSION
We propose an algorithm able to improve the
deblocking correction on flat areas. The new
principle of our method is to use the maximum
number of available pixels to correct a perceptible
boundary. Using this method, we improve the
gradation between different grey levels without
introduce ghost boundaries. We focus our study only
on this artefact because it is very annoying for the
eye and experienced as the major principle limitation
of all traditional deblocking corrections. Our
algorithm is a low-cost one, thanks to the facts that
it is a one pass algorithm and that calculations used
to detect and correct the boundaries are very simple.
Visual results show the real improvement of our
algorithm on pictures containing flat areas and the
benefits of a large block correction for high
compression rates. Moreover, this principle can be
very favourable for future implementation where
more than 8 bits would be used for the coding of the
pixel component values. Finally, even if the visual
results show that our method gives results more
pleasing for the eye, we underline the difficulty to
characterize this perceptual improvement with
currently available objective metrics. These metrics
are not very well correlated with the human
perception because they do not take into account
other artificial structure such as ghost boundaries
which are also annoying for the human eye. Further
experiments are currently in progress to include this
new characteristic in an objective metric and to
correlate the results with subjective tests.
REFERENCES
Gopinath, R., Lang, M., Guo, H., Odegard, J. (1994).
Wavelet-based post-processing of low bit rate
transform coded images. Proc. IEEE Int.Conf. Image
Processing.
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
38

Yang, Y., Galastanos, N.,Kastaggelos, A., (1995).
Projection-based spatially adaptive reconstruction of
block-transform compressed images. IEEE Trans.
Image Processing, vol. 4, pp.896-908.
Chou, J., Crouse, M., & Ramchandran, K., (1998). A
simple algorithm for removing blocking artefacts in
block-transform coded images; IEEE Signal
Processing Letters, vol. 5, pp. 33-35.
List, P., Joch, A., Lainema, J., Bjontegaard, G., &
Karczewicz, M, (2003). Adaptative Deblocking Filter
IEEE Transactions on Circuits and System for Video
Technology, vol. 13 , pp. 614- 619.
Kuo, C., Hsieh, R.J., (1995). Adaptive postprocessor for
block encoded images, IEEE Trans. Circuits Systems
Video Technology. vol5., pp 298-304.
Averbuch, A.Z., Schclar, A., Donoho, D., (2005).
Deblocking of Block-Transform Compressed Images
using Weighted Sums of Symmetrically Aligned
Pixels, IEEE Trans. on Image Processing, 14(2), 200-
212.
Pan, F., Lin, X., Rahardja, S., Lin, W., Ong, E., Yao, S.,
Lu, Z., Yang, X., (2004). A locally adaptive algorithm
for measuring blocking artifacts in images and videos,
Signal Processing: Image Communication19, pp. 499-
506.
Wang, Z., Sheikh H.R., Bovik, A.C., (2002). No-
reference perceptual quality assessment of JPEG
compressed images, IEEE International Conference
on Image Processing, pp. I-477-480.
Figure 12: From left to right: uncompressed picture, compressed picture, traditional methods, our method.
IMPROVEMENT OF DEBLOCKING CORRECTIONS ON FLAT AREAS AND PROPOSAL FOR A LOW-COST
IMPLEMENTATION
39
