PARAMETRIZATION, ALIGNMENT AND SHAPE OF SPHERICAL
SURFACES
Xiuwen Liu, John Bowers
Department of Computer Science, Florida State University, Tallahassee, FL, 32306, USA
Washington Mio
Department of Mathematics, Florida State University, Tallahassee, FL, 32306, USA
Keywords:
Surface parametrization, surface alignment, shape geodesics, shape of surfaces, shape metric, texture maps.
Abstract:
We develop parametrization and alignment techniques for shapes of spherical surfaces in 3D space with the
goals of quantifying shape similarities and dissimilarities and modeling shape variations observed within a
class of objects. The parametrization techniques are refinements of methods due to Praun and Hoppe and
yield parametric mesh representations of spherical surfaces. The main new element is an automated technique
to align parametric meshes for shape interpolation and comparison. We sample aligned surfaces at the vertices
of a dense common mesh structure to obtain a representation of the shapes as organized point-clouds. We
apply Kendall’s shape theory to these dense point clouds to define geodesic shape distance, to obtain geodesic
interpolations, and to study statistical properties of shapes that are relevant to problems in computer vision.
Applications to the construction of compatible texture maps for a family of surfaces are also discussed.
1 INTRODUCTION
The representation and analysis of 3D geometric
structures are fundamental problems in areas such as
computer vision and medical imaging. The practical
relevance of these problems is increasing vertically in
tandem with the fast evolution of scanning technolo-
gies that allow us to acquire geometric structural data
both at the macroscopic and microscopic levels. The
geometry of the outer contour of an object is of par-
ticular interest as it carries a rich amount of 3D visual
information that can enable us to classify and discern
objects, analyze patterns of variation, and model the
temporal evolution of their shapes in the presence of
dynamics. In this paper, we develop techniques for
constructing parametrizations and for aligning closed
surfaces of genus zero, which are presented as meshes
in 3D Euclidean space R
3
. An example of a closed
surface of genus zero – that is, a surface that can
be obtained as a deformation of a round sphere – is
shown in Figure 1. We apply the parametrization and
alignment methods to the following problems: (i) the
construction of compatible low-distortion meshes for
a family of surfaces; (ii) the interpolation of spheri-
cal shapes; (iii) the development of metrics to quan-
tify shape similarity and dissimilarity; (iv) the con-
struction of compatible texture maps for a family of
shapes; (v) the calculation of mean shapes. These
problems are all relevant to computer vision as they
arise in the modeling of variations in shape and ap-
pearance, for example, in 3D object recognition.
Unlike a curve that has a natural parametriza-
tion by the arc-length parameter, no such special
parametrization exists for a surface. As a conse-
quence, discrete models of surfaces used in prac-
tice often adopt representations involving highly non-
uniform samplings, especially for surfaces whose ge-
ometry exhibit thin and elongated parts, high curva-
ture areas, or other sharp features. Meshes represent-
ing such surfaces tend to exhibit many regions that
are either undersampled or oversampled and contain
many triangles with undesirable aspect ratios. To ad-
dress these issues, parametrizations of spherical sur-
faces by mappings that minimize the average geomet-
ric distortion have been investigated in (Praun and
Hoppe, 2003). Let S
2
denote the unit sphere cen-
tered at the origin in R
3
and let φ: S
2
→ M be a
parametrization of a spherical surface M embedded
in R
3
. The infinitesimal distortion produced by the
mapping φ at x ∈ S
2
was quantified by the sum of
199
Liu X., Bowers J. and Mio W. (2007).
PARAMETRIZATION, ALIGNMENT AND SHAPE OF SPHERICAL SURFACES.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 199-206
Copyright
c
 SciTePress

Figure 1: The contour of a bunny as a deformation of a round sphere.
the squares of the singular values of the derivative
dφ(x), the linearization of φ at x. However, this mea-
sure of distortion is heavily biased towards stretch-
ing and only mildly penalizes compression. This has
the practical effect of controlling undersampling of
the parametrizations – but not oversampling – and
allowing the parametrizations to distort aspect ratios
in a significant way. A solution to this problem was
proposed in (Praun and Hoppe, 2003), but the cost
function utilized is highly asymmetric with respect to
stretching and compression. In this paper, our con-
tribution to the construction of spherical parametriza-
tions is a refinement of the model of Praun and Hoppe
based on a fully symmetric measurement of distortion
that leads to more uniform meshes. The process of
remeshing a surface with this technique to improve
regularity is illustrated in Figure 3. From a more
technical perspective, we also introduce some alterna-
tive computational strategies for the implementation
of the parametrization algorithm.
The main new element of this paper is an algo-
rithm to align parametric surfaces of genus zero in a
fully automated manner. Alignment is of basic impor-
tance in shape interpolation and in the development
of shape metrics. Without alignment, interpolations
tend to be intuitively incorrect (Alexa, 2000). In sev-
eral previous works on shape interpolation, such as
(Alexa, 2000) and (Asirvatham et al., 2005), align-
ment is done with the aid of manually chosen land-
mark points. Here, alignment is based on an optimal
matching of the outward unit normal fields to the sur-
faces, which capture important geometric properties
to first order. Applied to a family of spherical sur-
faces, the parametrizaton and alignment methods al-
low us to obtain compatible parametrizations for the
family that, on average, optimally match correspond-
ing features and minimize metric distortions. Once
such family of parametrizations has been constructed,
one can remesh the given surfaces using a common
reference spherical triangulation of S
2
and use these
meshes for multiple purposes such as interpolating
shapes, defining shape metrics, studying the statis-
tics of shapes, and applying texture maps to the entire
family in a compatible fashion.
The paper is organized as follows. In Section
2, we describe an algorithmic procedure to construct
“regular” parametrizations of surfaces of genus zero.
Sections 3 and 4 are devoted to the problem of align-
ing surfaces. A brief review of Kendall’s shape model
is presented in Section 5.1, which is followed by ap-
plications to shapes of surfaces. Mean shapes are dis-
cussed in Section 6, as an introduction to the statisti-
cal study of shapes of surfaces.
2 PARAMETRIZATIONS
Let a closed surface of genus zero in R
3
be presented
as a mesh M. A spherical parametrization of M con-
sists of a spherical triangulation K of the sphere S
2
to-
gether with an embedding φ: S
2
→ M ⊆ R
3
such that
φ respects the mesh structures. Thus, vertices, edges
(that is, great circles connecting adjacent vertices) and
spherical triangles of K are mapped to the correspond-
ing structures in M. To construct parametrizations, we
normalize M by scaling it to have a fixed total area,
say, 4π.
For each x ∈M, let J
φ
−1
(x) denote the Jacobian of
the inverse map φ
−1
: M →S
2
at x, and let 0 < γ(x) ≤
Γ(x) be the singular values of J
φ
−1
(x). In (Praun and
Hoppe, 2003), the metric distortion of φ is quantified
by the average value of
1
γ
2
(x)
+
1
Γ
2
(x)
(1)
over M. If p = φ
−1
(x) ∈ S
2
, then the singular values
of J
φ
(p) are 1/γ(x) and 1/Γ(x). Thus, (1) is heav-
ily biased toward stretching due to φ, since sizable
stretching corresponds to small values of γ, while high
compression relates to large values of Γ. To address
this issue, a term proportional to the sixth power of Γ
is added to (1), but the proposed solution is rather ad
hoc and highly asymmetric with respect to stretching
and compression. We modify the cost function to the
average value of
log
2
γ(x) + log
2
Γ(x), (2)

which is perfectly symmetric in that stretching and
compression by the same factor are penalized iden-
tically. Note that, on a logarithmic scale, the mag-
nitude of the singular values of J
φ
−1
(x) and J
φ
(p) are
the same. Moreover, (2) vanishes precisely in the case
where both singular values are 1; that is, if there is no
infinitesimal distortion at x.
To estimate the cost function, Praun and Hoppe
subdivide the mesh K until each triangle is “suffi-
ciently” planar and approximate each spherical trian-
gle τ in the subdivided mesh by the planar triangle
τ
1
⊂ R
3
spanned by its vertices. Let T be a triangle
in the associated subdivision of M that corresponds
to τ via φ. Then, φ
−1
is approximated by the lin-
ear map A
T
: T → τ
1
determined by the vertex cor-
respondence. The singular values of J
φ
−1
(p) are ap-
proximated by the singular values of A
T
over the tri-
angle T, for any x ∈ T. However, if the triangles have
bad aspect ratio, large errors may occur in the esti-
mation of the singular values even after taking fine
subdivisions of K. To cope with this problem, they
precede the subdivision of K with another subdivi-
sion step that attempts to improve aspect ratios. We
adopt a different approach to a reliable estimation of
the singular values. We replace the linear approxima-
tion to each spherical triangle with the planar triangle
obtained via the exponential map, as described next.
Let v be the vertex of τ determined by its two longest
sides of length ℓ
1
and ℓ
2
, respectively, and let θ be the
internal angle at v. We approximate τ with the plane
triangle τ
2
determined by ℓ
1
,ℓ
2
and θ, as indicated
in Figure 2. Note that τ
2
is well defined up to rigid
motions, which will not affect singular values. The
advantage of τ
2
is that, for small triangles, it gives
a better approximation of the geometry of τ even for
nearly degenerate triangles. As before, the singular
values are estimated using the linear map T → τ
2
de-
termined by the vertex correspondence.
θ
v
Figure 2: A spherical triangle flattened via the exponential
map.
Praun and Hoppe employ a coarse-to-fine strategy
– analogous to that adopted in (Hormann et al., 1999)
and (Sander et al., 2002) – to construct a spherical em-
bedding that parameterizes M. The mesh M is deci-
mated sequentially until it is reduced to a tetrahedron.
This gives a multiresolution representation of M as
a sequence of meshes. A spherical parametrization
that minimizes the cost function is first constructed
at the coarse tetrahedral level and then progressively
refined through the various intermediate levels to a
parametrization of M with minimal distortion. We re-
fer the reader to (Praun and Hoppe, 2003) for further
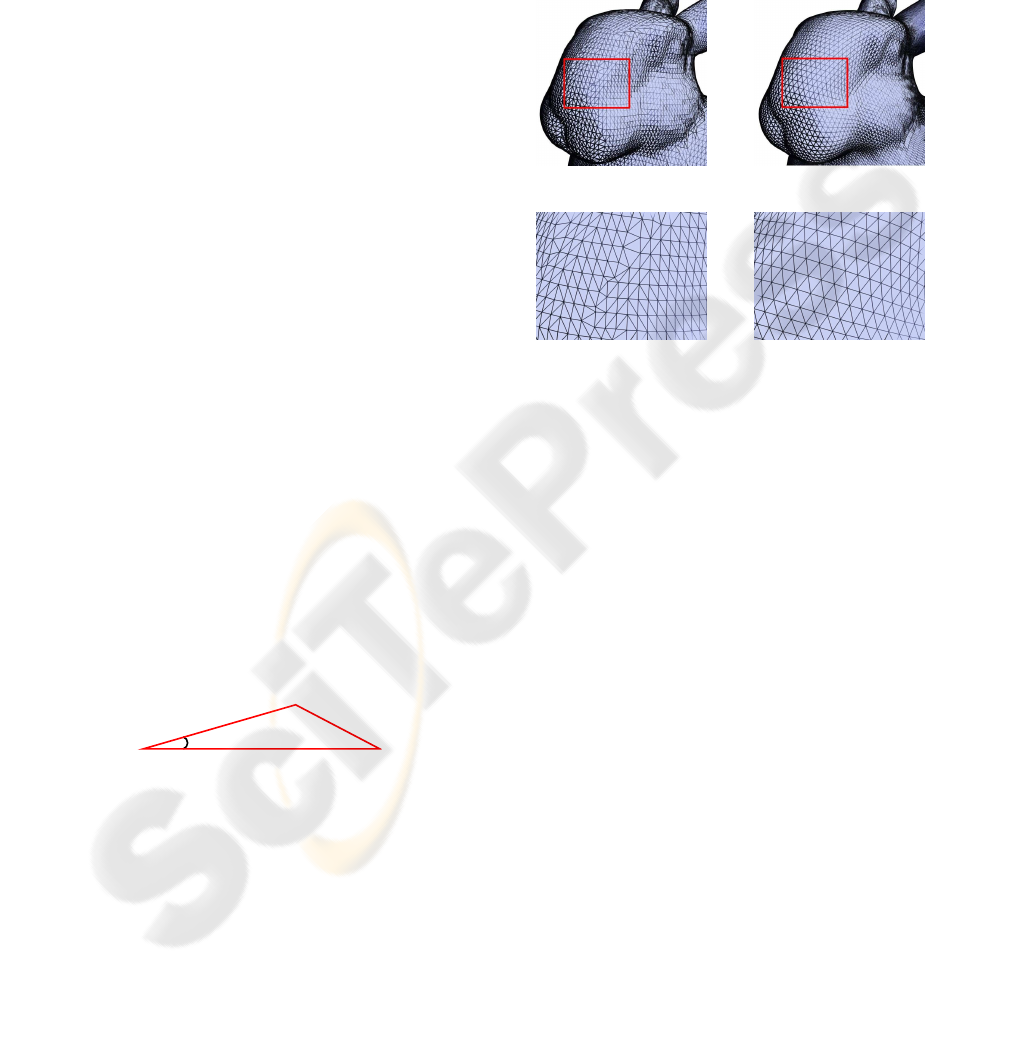
details. Figures 3 (a) and (b) show a mesh on a bunny
and the result of remeshing the shape by transferring
a regular mesh on the sphere via a minimal distor-
tion parametrization, respectively. A close-up view is
shown on panels (c) and (d). Note that the triangles
are much more regular in the remeshed surface.
(a) (b)
(c) (d)
Figure 3: Remeshing the surface of a bunny: (a) the original
mesh; (b) transferring a regular spherical mesh from S
2
with
a minimal-distortion parametrization; (c) and (d) are close-
up views.
Similar to (Gu et al., 2002), minimal-distortion
parametrizations can be used to transfer texture pat-
terns from the sphere S
2
to a shape as illustrated in
Figure 4.
3 SHAPE ALIGNMENT
Let M
1
and M
2
be meshes in 3D space representing
spherical surfaces. Using the procedure described in
Section 2, construct parametrizations φ
i
: S
2
→ M
i
,
for i = 1,2. Before aligning the shapes, we remesh
them with respect to a fixed triangulation K of S
2
, typ-
ically chosen to have fairly uniform triangles. Then,
each φ
i
can be viewed as a mapping K → M
i
that re-
spects the mesh structures. The idea is to consider
reparametrizations of one the shapes to best match the
geometry of the other using the alignment of the out-
ward unit normal fields as criterion. We first discuss
reparametrizations.
Given a parametric shape φ: S
2
→ M and a ro-
tation matrix R ∈ SO(3), we consider reparametriza-
tions of M of the form
p 7→ φ(R
T
p), (3)

Figure 4: Transferring texture from a sphere to a shape with a minimal-distortion parametrization.
which simply rotates the sphere S
2
before mapping it
to M via φ. We denote this new parametrization of
M by φ
R
. Note that the singular values of J
−1
φ
(x) and
J
φ
−1
R
(x) are the same, for any x ∈ M. Thus, if φ is
a minimal distortion parametrization, as measured by
(2), then φ
R
is also minimal.
Given a rotation matrix R and a pair of
parametrizations φ
1
and φ
2
R
, for each p ∈ S
2
, we
think of φ
1
(p) ∈M
1
and φ
2
R
(p) ∈M
2
as corresponding
points and wish to measure the average discrepancy
of the normal fields N
1
(p) and N
2
(p;R), for p ∈ S
2
.
Normal fields are insensitive to translations and scale,
but they do change under rotations and reflections of
a surface. Thus, before comparing the normal fields
of φ
1
and φ
2
R
, we find the orthogonal matrix U ∈ O(3)
that minimizes
S
2
kN
1
(p) −U (N
2
(p;R)) k
2
dp. (4)
In practice, the most interesting triangulations K of S
2
are those that are fairly dense and uniform. For these,
the minimizer of (4) can be estimated as
U
R
= argmin
U∈O(3)
∑
v∈K
kN
1
(v) −U (N
2
(v;R)) k
2
, (5)
where the sum is taken over the vertices v of K. The
solution to (5) can be computed in closed form, as
follows. Order the vertices of K as v
1
,. . . ,v
ℓ
and form
the 3×ℓ matrices P and Q
R
, whose jth columns are
the normal vectors N
1
(v
j
) and N
2
(v
j
;R), respectively.
Let the singular value decomposition of PQ
T
R
be given
by
PQ
T
R
= UΣW
T
, (6)
with V,W ∈ O(3) and Σ diagonal with nonnegative
eigenvalues. Then,
U
R
= UW
T
. (7)
The reparametrization of φ
2
that best aligns the
parametric shapes φ
1
,φ
2
: K → S
2
is determined by
the rotation matrix
ˆ
R = argmin
R∈SO(3)
H(R) , (8)
where
H(R) =
S
2
kN
1
(p) −U
R
(N
2
(p;R)) k
2
dp. (9)
4 ALIGNMENT ALGORITHM
The alignment of M
1
and M
2
is implemented in two
stages: first, we carry out a coarse estimation of
ˆ
R by
sampling the functional H over a large finite set of ro-
tations. Subsequently, a local refinement is performed
using a gradient search. An alternative stochastic gra-
dient procedure will be discussed elsewhere.
4.1 Coarse Estimation
Let η
1
,. . . ,η
s
be a fairly uniformly distributed and
dense collection of unit vectors to be thought of as
determining axis of rotations of R
3
. An example of
such a set is the collection of vertices of the triangula-
tion K of S
2
used in the previous section. Divide the
interval [0,2π] uniformly into r parts to obtain angles
0 = θ
0
< θ
1
< . .. < θ
r
= 2π. We sample H over the
set R(η
i
,θ
j
), 1 6 i 6 s, 1 6 j 6 r, of rotations about
the axis η
i
by the angle θ
j
. As in (5), for a rotation R,
the calculation of the functional H uses the following
discretization over the vertices of the mesh K:
H(R) =
∑
v∈K
kN
1
(v) −U
R
(N
2
(v;R)) k
2
. (10)
The top results are recorded and a finer search is car-
ried out around each of these candidates.
4.2 Local Refinement
The space SO(3) of 3 ×3 rotation matrices R is a
3-dimensional manifold (as a matter of fact, a Lie
group). To perform the aforementioned gradient
search, we first describe the tangent space to SO(3)
at R. Let
E
1
=


0 1 0
−1 0 0
0 0 0


, E
2
=


0 0 0
0 0 1
0 −1 0


,
E
3
=


0 0 1
0 0 0
−1 0 0


.
(11)

For any R ∈ SO(3), the matrices
E
R
i
=
1
√
2
RE
i
, (12)
1 6 i 6 3, form an orthonormal basis of the tangent
space to SO(3) at R. A geodesic deformation of R
along the direction E
R
i
is given by
R
i
(t) = Re
tE
i
/
√
2
. (13)
We estimate the partial derivatives of H in the direc-
tions E
R
i
, as follows:
∂
i
H(R) ≈
H(R
i
(ε)) −H(R)
ε
, (14)
with ε > 0 small. The gradient of H at R can be cal-
culated as
∇H(R) = RA
R
, (15)
where A
R
=
∑
3
i=1
∂
i
H(R)
√
2
E
i
. The (geodesic) update
rule for the gradient search is
R
j+1
= R
j
e
−δA
R
j
, (16)
with δ > 0 small.
5 SHAPE OF SURFACES
We employ the parametrization and alignment tech-
niques presented in Sections 2 and 3 to model
and quantify shape similarity and divergence within
a given collection of spherical meshes M
1
,. . . ,M
k
.
First, construct minimal distortion parametrizations
φ
i
: S
2
→ M
i
, 1 6 i 6 k. Choose a spherical trian-
gulation K of S
2
, which will be used to align and
discretize the parametrizations. Remesh all surfaces
with respect to K using the parametrizations φ
i
– we
abuse terminology and still refer to the new meshes as
M
i
. Each φ
i
can now be viewed as a mesh-preserving
mapping K → M
i
. To simplify the discussion, we
align each φ
j
, 2 6 j 6 k, with respect to φ
1
. This type
of alignment will be biased toward the first shape, so
refinements of the alignment will be discussed below.
An advantage of remeshing all surfaces over K is that
the alignment of the surfaces induce a natural corre-
spondence between the vertices of any pair M
i
and
M
j
, i 6= j. We exploit this fact to study the shapes of
the surfaces.
We order the vertices of K arbitrarily as v
1
,. . . ,v
n
and discretize each M
i
using the ordered point cloud
φ
i
(v
1
),. . .,φ
i
(v
n
). Since correspondences have been
established between the point clouds associated to any
pair of surfaces, we can resort to Kendall’s shape the-
ory to analyze the shapes of the surfaces (Kendall,
1984), (Kendall et al., 1999). We briefly review the
model, which uses a Procrustean alignment of shapes
and a geodesic metric to quantify shape divergence.
5.1 Kendall’s Model
For a parametric shape φ: K → M, we write the co-
ordinate vectors of the vertices φ(v
1
),. . .,φ(v
n
) as the
columns of a 3×n matrix P. Ordered configurations
of vertices that differ by rigid motions or scale are to
be viewed as having the same shape. To eliminate
translational effects from the representation, the or-
dered point cloud is translated to have its centroid at
the origin. This amounts to subtracting the mean
µ
φ
=
φ(v
1
) + . . . + φ(v
n
)
n
∈ R
3
(17)
from each column of the matrix P. To fix the scale,
a centered matrix P is normalized to have Frobenius
norm 1. Centered matrices of unit norm are referred
to as pre-shapes. Heretofore, we assume that all ma-
trices have been normalized to represent pre-shapes.
Unlike translation and scale, there is no standard
normalization that satisfactorily accounts for rotations
and reflections. This is due to the facts that rota-
tional alignment for shape comparison depends on
the shapes that are being compared in a more essen-
tial manner and the relevance of chirality tends to be
contextual. Given pre-shapes P,Q, the best alignment
in Kendall’s model is given by the orthogonal matrix
ˆ
U ∈ O(3) characterized by
ˆ
U = argmin
U∈O(3)
kP−UQk
2
. (18)
ˆ
U is the orthogonal transformation that places Q clos-
est to P as measured by the Frobenius norm. Using
a singular value decomposition, write PQ
T
= V
1
ΣV
T
2
,
with V
1
,V
2
∈ O(3) and Σ diagonal with nonnegative
eigenvalues. Then,
ˆ
U = V
1
V
T
2
. The shape distance is
the geodesic distance between the pre-shapes P and
ˆ
Q =
ˆ
UQ, which can be expressed as
d(P,Q) = arccos(trΣ). (19)
Moreover, if P 6=
ˆ
Q, the geodesic deformation be-
tween P and
ˆ
Q is given by
Λ(t) = cos(ωt)P+ sin(ωt)
ˆ
Q−(trΣ) P
k
ˆ
Q−(trΣ) Pk
, (20)
where ω = arccos(trΣ) and 0 ≤ t ≤ 1.
5.2 Algorithm
The following algorithmic steps compute the Kendall
geodesic between the shapes represented by the pre-
shapes P and Q:
1. Find a singular value decomposition PQ
T
=
V
1
ΣV
T
2
.
2. Set
ˆ
Q = V
1
V
T
2
Q.
3. If P =
ˆ
Q, the geodesic is represented by the con-
stant path Λ(t) = P. Else, it is given by (20).

Figure 5: A shape geodesic with a compatible texture map applied to the deformation.
5.3 Examples of Geodesics
An example of a geodesic interpolation between a
horse and a cow is shown in Figure 5. To calculate
the geodesic, we first remesh the shapes to be interpo-
lated over a common spherical triangulation K of S
2
and align them using the algorithm of Section 4. Sub-
sequently, the point clouds given by the vertices of the
meshes are interpolated using Kendall’s model. The
point-cloud interpolation between the (ordered) ver-
tex sets is displayed in Figures 6 (a)–(e). At any stage
of the interpolation, the vertices of K are in correspon-
dence with the point cloud. Thus, the mesh structure
on K can used at all stages of the geodesic path to
obtain meshes as indicated in the last row of Figure
6. As exemplified in Figure 5, these aligned spherical
parametrizations allows us to apply texture maps to
the entire path in a compatible manner.
6 FR
´
ECHET MEAN SHAPES
To illustrate the usefulness of the algorithm for calcu-
lating shape geodesics in the study of shape statistics,
we indicate how one can define the notion of mean
shape using a natural extension of Fr
´
echet means in
Kendall’s theory (Kendall et al., 1999). If s
1
,. . . ,s
r
are spherical shapes, a mean shape will be defined as
follows. First, parameterize all shapes over a com-
mon spherical mesh K and align them all with respect
to, say, the first one. This fixes a parametrization for
each of the shapes. Let P
1
,. . . ,P
r
be the pre-shapes
associated with the vertices of the meshes induced by
these parametrizations over K. Then, a mean of the
family is a shape represented by a pre-shape P that
minimizes the scatter function
V(P) =
1
2
r
∑
i=1
d
2
(P,P
i
). (21)
Techniques for calculating the mean in Kendall’s the-
ory are discussed, e.g., in (Karcher, 1977). Figure 9
shows the mean of 4 horses. As well documented in
the literature, in other contexts, once the sample mean
of a collection has been computed, one can estimate
probability models for the family using the exponen-
tial map at the mean and tangent-space statistics (Dry-
den and Mardia, 1998).
7 SUMMARY AND CONCLUSION
We developed techniques to produce parametric rep-
resentations φ: S
2
→ M of spherical surfaces that re-
fine the methods of (Praun and Hoppe, 2003). The
parametrizations are constructed so as to minimize the
overall distortion in geometry. A method for align-
ing parametric surfaces to best match their unit nor-
mal fields was introduced. The procedure is fully
automated and can be used to quantify shape simi-
larity and divergence, and to model shape variations
observed within a class of objects. In conjunction
with Kendall’s shape theory, the alignment technique
yields a metric for shape comparison and geodesic
shape morphing technique. Applications to the con-
struction of compatible texture maps for a family of
surfaces and the calculation of mean shapes were dis-
cussed.

Figure 6: A geodesic interpolation between ordered point clouds. The first and last frames display the shapes to be interpolated
and the intermediate frames show 3 stages of the deformation.
Figure 7: Close-up view of the evolution of the mesh structure associated with the point clouds in Figure 6.
Alignment of shapes is based on reparametriza-
tions of a shape by rotations of the sphere S
2
. This
is natural in the proposed setting since the action of
rotations preserve the minimal-distortion property of
a parametrization. In future work, the alignment tech-
nique will be refined to an elastic alignment to bet-
ter match the geometric features of the surfaces. The
Kendall model of shapes was applied to a dense point
cloud representing a surface. While this is already
very useful and attractive from a computational stand-
point due to the simplicity of the model, the shape
metric fails to incorporate important higher order sur-
face geometry. The shape metric and interpolation
technique will also be refined to a model that can be
computed efficiently and which takes higher order ge-
ometry into account.
ACKNOWLEDGMENTS
This work was supported in part by NSF grants CCF-
0514743 and IIS-0307998, and ARO grant W911NF-
04-01-0268.
REFERENCES
Alexa, M. (2000). Merging polyhedral shapes with scat-
tered features. The Visual Computer, 16(1):26–37.
Asirvatham, A., Praun, E., and Hoppe, H. (2005). Consis-
tent spherical parametrization. In Workshop on Com-
puter Graphics and Geometric Modeling (CGGM).
Dryden, I. L. and Mardia, K. V. (1998). Statistical Shape
Analysis. John Wiley & Son.
Gu, X., Gortler, S., and Hoppe, H. (2002). Geometry im-
ages. In ACM SIGGRAPH 2002, pages 355–361.
Hormann, K., Greiner, G., and Campagna, S. (1999). Hi-
erarchical parametrization of triangulated surfaces. In
Vision, Modeling, and Visualization, pages 219–226.
Karcher, H. (1977). Riemann center of mass and mollifier
smoothing. Comm. Pure Appl. Math., 30:509–541.
Kendall, D. G. (1984). Shape manifolds, Procrustean met-
rics and complex projective spaces. Bull. London
Math. Soc., 16:81–121.
Kendall, D. G., Barden, D., Carne, T. K., and Le, H. (1999).
Shape and Shape Theory. Wiley, Chichester, New
York.
Praun, E. and Hoppe, H. (2003). Spherical parametriza-
tion and remeshing. In ACM SIGGRAPH 2003, pages
340–349.
Sander, P., Gortler, S., Snyder, S., and Hoppe, H. (2002).
Signal-specialized parametrization. In Eurographics
Workshop on Rendering, pages 87–100.

Figure 8: An example of a shape geodesic morphing a horse into another horse.
Figure 9: Four horses and their Fr
´
echet mean shape, which is shown on the bottom-right panel.