
A LEARNING APPROACH TO CONTENT-BASED IMAGE
CATEGORIZATION AND RETRIEVAL
Washington Mio
Department of Mathematics, Florida State University, Tallahassee, FL, 32306, USA
Yuhua Zhu, Xiuwen Liu
Department of Computer Science, Florida State University, Tallahassee, FL, 32306, USA
Keywords:
Content-based image retrieval, image categorization, image indexing, machine learning, spectral components,
dimension reduction, discriminant analysis.
Abstract:
We develop a machine learning approach to content-based image categorization and retrieval. We represent
images by histograms of their spectral components associated with a bank of filters and assume that a training
database of labeled images – that contains representative samples from each class – is available. We employ a
linear dimension reduction technique, referred to as Optimal Factor Analysis, to identify and split off “optimal”
low-dimensional factors of the features to solve a given semantic classification or indexing problem. This
content-based categorization technique is used to structure databases of images for retrieval according to the
likelihood of each class given a query image.
1 INTRODUCTION
In this paper, we investigate machine learning tech-
niques for dimension reduction and optimal discrim-
ination, and apply them to content-based categoriza-
tion and retrieval of images. Large image libraries –
such as those found in the World Wide Web and in
surveillance and medical databases – are generating a
pressing demand for intelligent and scalable systems
that can be trained to index and retrieve images ac-
cording to their contents in a fully automated manner.
Classical approaches based on “expert” annotations
are simply not a viable option in the presence of mas-
sive amounts of data.
For the image categorization problem, we shall as-
sume that a training database containing labeled im-
ages representing various different classes is available
and the goal is to learn optimal low-dimensional fea-
tures or “signatures” that can be used to assign a new
query image to the correct class. In content-based im-
age retrieval, the objective is to find the top ℓ matches
in a database to a query image, where the number ℓ
is prescribed by the user. In the proposed approach,
retrieval and categorization are closed related. We
will use a categorization algorithm to organize a large
database according to features learned from a training
set. Given a query image I, we will use this organi-
zation to estimate the probability that I is associated
with a given class and we will retrieve images accord-
ing to these probabilities.
The problem of classifying images in a database
into semantic categories arises in many different lev-
els of generality: for example, the problem can be as
broad as separating images that depict an indoor or
outdoor scene, or it may involve much more specific
categorization into classes such as cars, people, and
flowers. As the breadth of the semantic categories
may vary considerably, the development of general
strategies poses significant challenges. This moti-
vated us to approach the problem in two stages. First,
we extract “stable” features that are able to capture a
large amount of information about the structure and
semantic content of an image. Subsequently, we use
learning techniques to identify the factors that have
the highest discriminating power for a particular clas-
sification problem.
The histogram of an image carries very useful in-
formation, however, it tends to have only limited dis-
criminating ability because it encodes the statistics of
pixel values, but ignores their relative positions in the
image. To remedy the situation, we propose to use
histograms of various spectral components of an im-
36
Mio W., Zhu Y. and Liu X. (2007).
A LEARNING APPROACH TO CONTENT-BASED IMAGE CATEGORIZATION AND RETRIEVAL.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 36-43
Copyright
c
SciTePress

age as they retain a significant amount of informa-
tion about texture patterns and edges. The statistics
of spectral components have been used in the past pri-
marily in the context of texture analysis and synthe-
sis. In (Zhu et al., 1998), it is demonstrated that mar-
ginal distributions of spectral components suffice to
characterize homogeneous textures; other studies in-
clude (Portilla and Simoncelli, 2000) and (Wu et al.,
2000). To provide some preliminary evidence of the
discriminating power of spectral histogram (SH) fea-
tures, in Section 3, we report the results of a retrieval
experiment on a database of 1,000 images represent-
ing 10 different semantic categories. The relevance of
an image is determined by the nearest-neighbor cri-
terion applied to a number of SH-features combined
into a single vector. Even without a learning compo-
nent, we already obtain performances comparable to
those exhibited by many existing retrieval systems.
Learning techniques will be employed with a
twofold purpose: (a) to identify and split off the most
relevant factors of the SH-features for the discrimina-
tion of various categories of images; (b) to lower the
dimension of the representation to reduce complex-
ity and improve computational efficiency. We adopt
a learning strategy that will be referred to as Optimal
Factor Analysis (OFA) – a preliminary form of OFA
was introduced in (Liu and Mio, 2006) as Splitting
Factor Analysis. Given a (small) positive integer k,
the goal of OFA is to find an “optimal” k-dimensional
linear reduction of the original image features for a
particular categorization or indexing problem. Image
categorization and retrieval will be based on the near-
est neighbor classifier applied to the reduced features,
as explained in more detail below. We employ OFA
in the context of SH-features, but it will be presented
in a more general feature learning framework.
Image retrieval strategies employing a variety of
methods have been investigated in (Wang et al.,
2001), (Carson et al., 1999), (Rubner et al., 1997),
(Smith and Li, 1999), (Yin et al., 2005), (Hoi et al.,
2006). Further references can be found in these pa-
pers. Some of these proposals employ a relevance
feedback mechanism in an attempt to progressively
improve the quality of retrieval. Although not dis-
cussed in this paper, a feedback component can be
incorporated to the proposed strategy by gradually
adding to the training set images for which the quality
of retrieval was low.
A word about the organization of the paper. In
Section 2, we describe the histogram features that will
be used to characterize image content. Preliminary re-
trieval experiments using these features are described
in Section 3. Section 4 contains a discussion of Opti-
mal Factor Analysis, and Sections 5 and 6 are devoted
to applications of the machine learning methodology
to image categorization and retrieval. Section 7 closes
the discussion with a summary and a few remarks on
refinements of the proposed methods.
2 SPECTRAL HISTOGRAM
FEATURES
Let I be a gray-scale image and F a convolution filter.
The spectral component I
F
of I associated with F is
the image I
F
obtained through the convolution of I
and F, which is given at pixel location p by
I
F
(p) = F ∗ I(p) =
∑
q
F(q)I(p− q), (1)
where the summation is taken over all pixel locations.
For a color image, we apply the filter to its R,G,B
channels. For a given set of bins, which will be as-
sumed fixed throughout the paper, we let h(I,F) de-
note the corresponding histogram of I
F
. We refer to
h(I, F) as the spectral histogram (SH) feature of the
image I associated with the filter F. If the number of
bins is b, the SH-feature h(I,F) can be viewed as a
vector in R
b
. Figure 1 illustrates the process of ob-
taining SH-features. Frames (a) and (b) show a color
image and its red channel response to a Laplacian fil-
ter, respectively. The last panel shows the 11-bin his-
togram of the filtered image.
(a) (b)
(c)
Figure 1: (a) An image; (b) the red-channel response to a
Laplacian filter; (c) the associated 11-bin histogram.
If F = {F
1
,.. . ,F
r
} is a bank of filters, the SH-
features associated with the family F is the collec-
tion h(I,F
i
), 1 6 i 6 r, combined into the single m-
dimensional vector
h(I, F) = (h(I,F
1
),. .. ,h(I,F
r
)), (2)

where m = rb. For a color image, m = 3rb. Banks of
filters used in this paper typically include Gabor filters
of different widths and orientations, gradient filters,
and Laplacian of Gaussians.
3 SH-FEATURES FOR
RETRIEVAL
To offer some evidence that SH-features are desirable
for image retrieval, we perform a preliminary retrieval
experiment using the Euclidean distance between his-
tograms. To be able to compare the results with those
reported in (Wang et al., 2001), we use the same sub-
set of the Corel data set consisting of 10 semantic cat-
egories, each with 100 images. We refer to this data
set as Corel-1000. The categories are listed in Table
1 and three samples from each category are shown
in Figure 2. As the examples suggest, even within a
semantic category, significant variations are observed
among the images.
Table 1: Image categories in Corel-1000.
1 African People & Villages
2 Beach Scenes
3 Buildings
4 Buses
5 Dinosaurs
6 Elephants
7 Flowers
8 Horses
9 Mountains & Glaciers
10 Food
We utilize a bank of 5 filters and apply each fil-
ter to the R, G, and B channels of the images to ob-
tain a total of 15 histograms per image. Each his-
togram consists of 11 bins so that the SH-feature vec-
tor h(I,F) has dimension 165. For a query image
I from the database, we calculate the Euclidean dis-
tances between h(I,F) and h(J,F), for every J in the
database, and rank the images according to increas-
ing distances. For comparison purposes, as in (Wang
et al., 2001), we calculate the weighted precision and
the average rank, which are defined next. The re-
trieval precision for the top ℓ returns, is n
ℓ
/ℓ, where
n
ℓ
is the number of correct matches. The weighted
precision for a query image I is
p(I) =
1
100
100
∑
ℓ=1
n
ℓ
ℓ
. (3)
For a query image I, rank order all 1,000 images in
the database, as described above. The average rank
r(I) is the mean value of the ranks of all images that
belong to the same class as I. Figures 3(a) and 3(b)
show the mean values
¯p
i
=
1
100
∑
I∈C
i
p(I) and ¯r
i
=
1
100
∑
I∈C
i
r(I), (4)
of the weighted precision and average rank within
each class C
i
, 1 6 i 6 10. High retrieval performance
is reflected in high mean precision and low mean rank.
Note that even without a learning component, the re-
sults obtained using SH-features and SIMPLIcity are
essentially comparable. Both perform considerably
better than color histograms with the earth mover’s
distance (EMD) investigated in (Rubner et al., 1997).
In Figure 3, color histograms 1 and 2 refer to EMD
applied to histograms with a different number of bins.
The results for SIMPLIcity and color histograms have
been reported in (Wang et al., 2001).
4 OPTIMAL FACTOR ANALYSIS
We introduce Optimal Factor Analysis (OFA), a lin-
ear feature learning technique whose goal is to find
a linear mapping that reduces the dimension of the
data representation while optimizing the discrimina-
tive ability of the K-nearest neighbor (KNN) classi-
fier as measured by its performance on given train-
ing data. We assume that a given ensemble of data
in Euclidean space R
m
is divided into training and
cross-validation sets, each consisting of labeled rep-
resentatives from P different classes of objects. For
an integer c, 1 ≤ c ≤ P, we denote by x
c,1
,.. .,x
c,t
c
and y
c,1
,.. . ,y
c,v
c
the training and cross-validation el-
ements that belong to class c.
If A: R
m
→ R
k
is a linear transformation, the
quantity
ρ(y
c,i
;A) =
min
c6=b, j
kAy
c,i
− Ax
b, j
k
p
min
j
kAy
c,i
− Ax
c, j
k
p
+ ε
(5)
provides a measurement of how well the nearest-
neighbor classifier applied to the transformed data
identifies the cross-validation element y
c,i
as belong-
ing to class c. Here, ε > 0 is a small number used
to prevent vanishing denominators and p > 0 is an
exponent that can be adjusted to regularize ρ in dif-
ferent ways. In this paper, we set p = 2. A large
value of ρ(y
c,i
;A) indicates that, after the transforma-
tion A is applied, y
c,i
lies much closer to a training
sample of the class it belongs to than to those of other
classes. A value ρ(y
c,i
;A) ≈ 1 indicates a transition
between correct and incorrect decisions by the near-
est neighbor classifier. The special case of the func-
tion ρ, where p = 1, was used in the development of

Figure 2: Samples from the dataset Corel-1000: three images from 10 classes, each consisting of 100 images.
1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Category ID
Average Precision
1 2 3 4 5 6 7 8 9 10
0
100
200
300
400
500
600
Category ID
Average Rank
Figure 3: (a) Plots of ¯p
i
and ¯r
i
, 1 6 i 6 10. The methods are labeled as follows: (▽) spectral histogram; (∗) SIMPLIcity; (◦)
color histogram 1; (+) color histogram 2.
Optimal Component Analysis (Liu et al., 2004). Note
that expression (5) can be easily modified to reflect
the performance of the KNN classifier.
The idea is to choose a transformation A that max-
imizes the average value of ρ(y
c,i
;A) over the cross-
validation set. To control bias with respect to partic-
ular classes, we scale ρ(y
c,i
;A) with a sigmoid of the
form
σ(x) =
1
1+ e
−βx
(6)
before taking the average. We identify linear maps
A: R
m
→ R
k
with k × m matrices, in the usual way,
and define a performance function F : R
k×m
→ R by
F(A) =
1
P
P
∑
c=1
1
v
c
v
c
∑
i=1
σ(ρ(y
c,i
;A) − 1)
!
. (7)
Scaling an entire dataset does not change deci-
sions based on the nearest-neighbor classifier. This is
reflected in the fact that F is (nearly) scale invariant;
that is, F(A) ≈ F(rA), for r > 0. Equality does not
hold exactly if ε 6= 0, but in practice, ε is negligible.
Thus, we fix the scale and optimize F over matrices A
of unit Frobenius norm. Let
S =
n
A ∈ R
k×m
: kAk
2
= tr(AA
T
) = 1
o
(8)
be the unit sphere in R
k×m
. The goal of OFA is to
maximize the performance function F over S; that is,
to find
ˆ
A = argmax
A∈S
F(A). (9)
Due to the existence of multiple local maxima of F,
the numerical estimation of
ˆ
A is carried out with a
stochastic gradient search. We omit the details since

the optimization strategy is similar to that employed
in (Liu et al., 2004), but much simpler because the
search is performed over a sphere instead of a Grass-
mann manifold.
4.1 An Interpretation of OFA
We interpret the dimension reduction via a linear map
A: R
m
→ R
k
and the Euclidean metric in the reduced
space in terms of the original m-dimensional features.
If A is a rank r matrix, take a singular value decom-
position
A = UΣV
T
, (10)
where U and V are orthogonal matrices of dimen-
sions k and m, respectively, and Σ is a k × m matrix
whose r× r northwest quadrant is diagonal with posi-
tive eigenvalues and whose remaining entries are all
zero. Let H be the r-dimensional subspace of R
m
spanned by the first r columns of V and denote the
orthogonal projection of a vector x ∈ R
m
onto H by
x
H
. Then,
Ax· Ay = y
T
(A
T
A)x = y
T
Kx = y
T
H
Kx
H
, (11)
for any x, y ∈ R
m
, where K = A
T
A is a positive semi-
definite symmetric matrix. In particular,
kAx− Ayk
2
= (x
H
− y
H
)
T
K(x
H
− y
H
). (12)
This means that the Euclidean distance between fea-
ture vectors in the reduced space R
k
can be interpreted
as the distance between the projected vectors x
H
and
y
H
in the original feature space with respect to the
new metric
d(x
H
,y
H
) =
q
(x
H
− y
H
)
T
K(x
H
− y
H
). (13)
Note that the subspace H is spanned by the eigenvec-
tors of K associated with its non-zero eigenvalues, so
that (13) does define a metric on H. Thus, OFA can
be viewed as a technique to learn from a training set
an optimal subspace of the feature space R
m
for di-
mension reduction and an inner product whose asso-
ciated metric is optimal for categorization based on
the nearest-neighbor classifier.
4.2 A Leave-One-Out Strategy
In applications of OFA to image retrieval, or in sit-
uations where the training set is not very large, a
leave-one-out strategy is adopted during the optimiza-
tion process. In other words, for a candidate linear
map A, the value F(A) of the performance function
is replaced with the average value of F over several
passes, as follows. In each pass, the cross-validation
set consists of a single element taken from the train-
ing set and F(A) is calculated according to (7). Then,
the average value over the entire training set is used
to quantify performance in the optimization process.
5 IMAGE CATEGORIZATION
We report the results of several image categorization
experiments with the Corel-1000 data set described
in Section 3. In each experiment, we placed an equal
number of images from each class in the training set
and used the remaining ones as query images to be
indexed by the nearest neighbor classifier applied to
a reduced feature learned with OFA. Initially, an im-
age is represented by an SH-feature vector h(I,F) of
dimension 165 obtained from the 11-bin histograms
associated with 5 filters applied to the R, G, and B
channels; OFA was used to reduce the dimension to
k = 9. Table 2 shows the categorization performance:
T denotes the total number of images in the training
set, and categorization performance refers to the rate
of correct indexing using all 1,000− T images out-
side the training set as queries.
Table 2: Results of categorization experiments with the
Corel-1000 data set. T is the number of training images
and the dimension of the reduced feature space is 9.
T Categorization Performance
600 84.5%
400 84.3%
200 73.9%
6 IMAGE RETRIEVAL
We now use the classifier learned for content-based
image categorization to retrieve images according to
their contents. We begin with the remark that the clas-
sifier was optimized to categorize query images cor-
rectly according to the nearest neighbor criterion, but
not necessarily to rank matches to a query image cor-
rectly according to distances in feature space. Thus,
in contrast with the retrieval strategy based solely on
distances adopted, e.g., in (Wang et al., 2001) and
(Hoi et al., 2006), we propose to exploit the strengths
of the image categorization classifier in a more essen-
tial way.
Let A: R
m
→ R
k
be the optimal linear dimension-
reduction map learned with OFA. If I is an image and
h(I, F) ∈ R
m
is the associated SH-feature vector, we
let x denote its projection to R
k
; that is,
x = Ah(I,F). (14)
If there are P classes of images, for each i, 1 6 i 6
P, let x
i
be the reduced feature vector of the training
image in class i, which is closest to x. To each i, we
assign a probability p(i|I) that I belongs to class i, as

1 2 3 4 5 6 7 8 9 10
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Category ID
Average Precision
1 2 3 4 5 6 7 8 9 10
0
50
100
150
200
250
300
350
Category ID
Average Rank
(a) (b)
Figure 4: (a) Average precision within each class; (b) average rank. The methods are labeled as follows: (▽) spectral
histogram; (∗) SIMPLIcity; (△) OFA-400.
follows:
p(i|I) =
e
−kx−x
i
k
2
∑
P
j= 1
e
−kx−x
j
k
2
. (15)
Given a query image I and a positive integer ℓ, the
goal is to retrieve a ranked list of ℓ images from the
database. We assume that all images in the database
havebeen indexedaccordingto content using the clas-
sifier learned with OFA. Rank the classes according
to the probabilities p(i|I). We retrieve images as fol-
lows: select as many images as possible from the most
likely class; once that class is exhausted, we proceed
similarly with the second most likely class and iter-
ate the procedure until ℓ images are obtained. Within
each class, the images are retrieved and ranked ac-
cording to their Euclidean distances to I as measured
in the reduced feature space.
6.1 Experimental Results
We report the results of retrieval experiments with the
Corel-1000 dataset. To quantify performance in an
objective manner, we only use query images that are
part of the database. Since each class contains 100
images, the maximum possible number of matches to
a query image is 100, where a match is an image that
belongs to the same class. We first compare retrieval
results using OFA learning with those obtained with
SIMPLIcity and spectral histograms, as described in
Section 3. We calculated the mean values ¯p
i
and ¯r
I
of
the weighted precision and rank as defined in (4). The
plots shown in Figure 4 show a significant improve-
ment in retrieval performance with a learning compo-
nent. OFA was used with 400 training images.
We further quantify retrieval performance, as fol-
lows. For an image I and a positive integer ℓ, let m
ℓ
be the number of matching images among the top ℓ
returns. Define
p
ℓ
(I) =
m
ℓ
(I)
ℓ
and r
ℓ
(I) =
m
ℓ
(I)
100
, (16)
which are the precision and recall rates for ℓ returns
for image I. The average precision and average recall
for the top ℓ returns are defined as
p
ℓ
=
∑
I
p
ℓ
(I)
1000
and r
ℓ
=
∑
I
r
ℓ
(I)
1000
, (17)
respectively. Here, the sum is taken over all 1,000 im-
ages in the database. Note that, for a perfect retrieval
system, p
ℓ
= 1, for 1 6 ℓ 6 100, and gradually decays
to p
1000
= 0.1; similarly r
ℓ
= 1, for ℓ ≥ 100 decaying
to r
1
= 0.01.
Table 3 shows several values of the average pre-
cision and average recall based on a 9-dimensional
classifier learned with T training images. The full
average-precision-recall plots are shown in Figure 5.
Figure 6 shows the top 10 returns for a few images
in the database for a classifier trained with T = 400
images. In each group, the first image is the query
image, which is also the top return.
7 CONCLUSION
We represented images using histograms of their
spectral components for content-based image cate-
gorization and retrieval. A learning technique was
developed to reduce the dimension of the represen-
tation and optimize the discriminative ability of the
nearest-neighbor classifier. Several experiments were
carried out and the results indicate a very significant
improvement in retrieval performance over a number
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Precision
Recall
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Precision
Recall
0 0.2 0.4 0.6 0.8
0
0.2
0.4
0.6
0.8
1
Precision
Recall
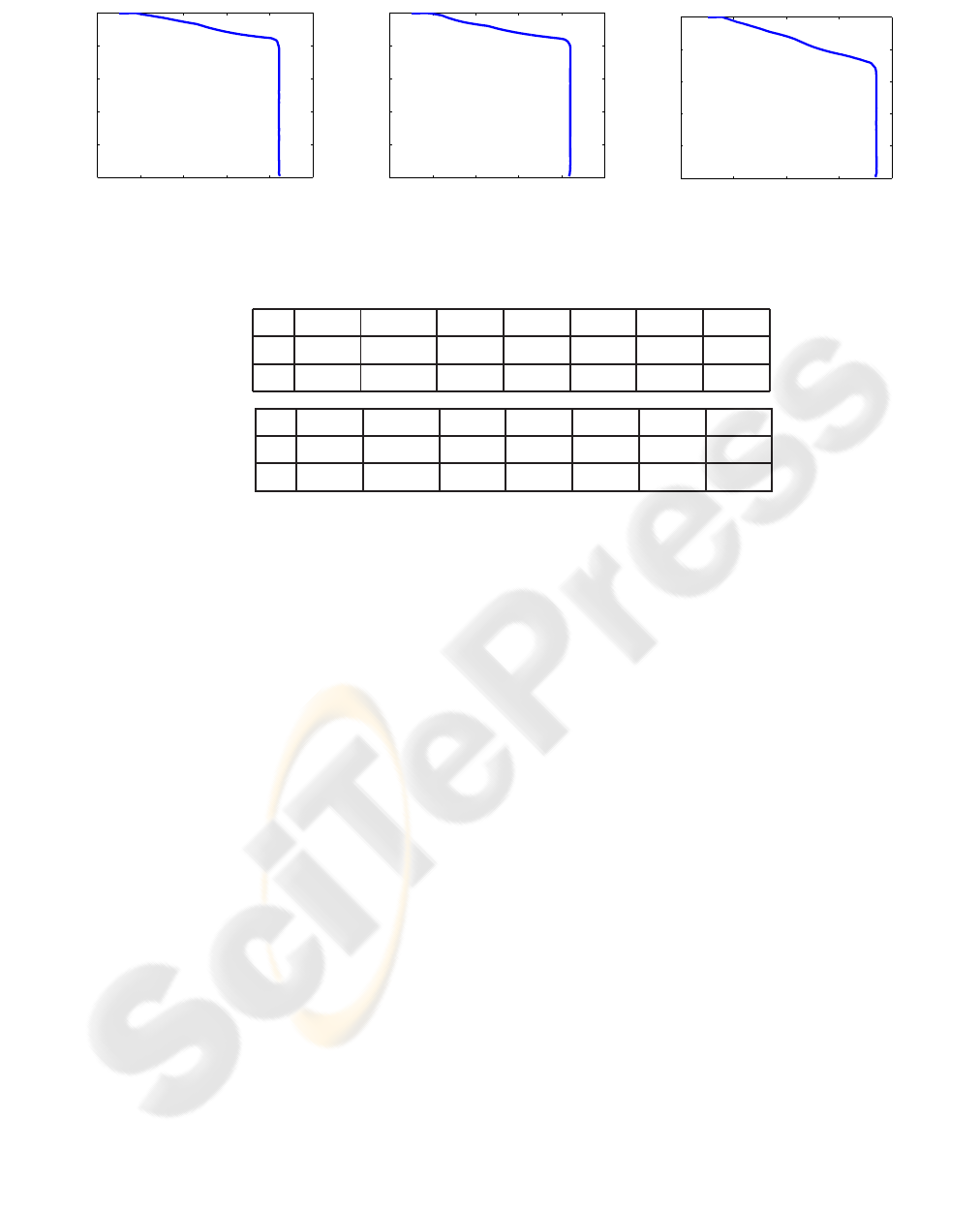
Figure 5: Corel-1000: plots of the average-precision × average-recall for 600, 400, and 200 training images.
Table 3: Retrieval results with T training images. Average retrieval precision (p
ℓ
) and recall (r
ℓ
) for the top ℓ matches.
T = 600
ℓ 10 20 40 70 100 200 500
p
ℓ
0.842 0.0842 0.843 0.843 0.832 0.466 0.198
r
ℓ
0.084 0.168 0.337 0.590 0.832 0.930 0.992
T = 400
ℓ 10 20 40 70 100 200 500
p
ℓ
0.840 0.0840 0.840 0.841 0.828 0.460 0.199
r
ℓ
0.084 0.168 0.336 0.589 0.828 0.919 0.996
of existing retrieval systems. Refinements to obtain
sparse representations and incorporate kernel tech-
niques to cope with nonlinearity in data geometry, re-
trieval strategies for real-time execution, as well as a
user feedback component will be investigated in fu-
ture work.
ACKNOWLEDGEMENTS
This work was supported in part by NSF grants CCF-
0514743 and IIS-0307998, and ARO grant W911NF-
04-01-0268.
REFERENCES
Carson, C., Thomas, M., Belongie, S., Hellerstein, J., and
Malik, J. (1999). Blobworld: a system for region-
based image indexing and retrieval. In Proc. Visual
Information Systems, pages 509–516.
Hoi, S., Liu, W., Lyu, M., and Ma, W.-Y. (2006). Learning
distance metrics with contextual constraints for image
retrieval. In Proc. CVPR 2006.
Liu, X. and Mio, W. (2006). Splitting factor analysis and
multi-class boosting. In Proc. ICIP 2006.
Liu, X., Srivastava, A., and Gallivan, K. (2004). Optimal
linear representations of images for object recogni-
tion. IEEE Trans. Pattern Analysis and Machine In-
telligence, 26:662–666.
Portilla, J. and Simoncelli, E. (2000). A parametric texture
model based on joint statistics of complex wavelet co-
eficients. International Journal of Computer Vision,
40:49–70.
Rubner, Y., Guibas, L., and Tomasi, C. (1997). The
earth mover’s distance, multi-dimensional scaling,
and color-based image databases. In Proc. DARPA Im-
age Understanding Workshop, pages 661–668.
Smith, J. and Li, C. (1999). Image classification and query-
ing using composite region templates. Computer Vi-
sion and Image Understanding, 75(9):165–174.
Wang, J., Li, J., and Wiederhold, G. (2001). SIMPLIcity:
Semantics-sensitive integrated matching for picture li-
braries. IEEE Trans. on Pattern Analysis and Machine
Intelligence, 23(9):947–963.
Wu, Y., Zhu, S., and Liu, X. (2000). Equivalence of Julesz
ensembles and FRAME models. International Jour-
nal of Computer Vision, 38:247–265.
Yin, P.-Y., Bhanu, B., Chang, K.-C., and Dong, A. (2005).
Integrating relevance feedback techniques for im-
age retrieval using reinforcement learning. IEEE
Trans. on Pattern Analysis and Machine Intelligence,
27(10):1536–1551.
Zhu, S., Wu, Y., and Mumford, D. (1998). Filters, random
fields and maximum entropy (FRAME). International
Journal of Computer Vision, 27:1–20.

(a)
(b)
(c)
(d)
(e)
Figure 6: Examples of top ten returns. In each group, the first image is the query, which is also the top return.
