A ROBUST WATERMARKING SCHEME BASED ON EDGE

DETECTION AND CONTRAST SENSITIVITY FUNCTION

John N. Ellinas

Department of Electronic Computer Systems,Technological Education Institute of Piraeus, 12244 Egaleo, Greece

Dimitrios E. Manolakis

Department of Automation, Alexander Technological Education Institute of Thessaloniki, 57400 Thessaloniki, Greece

Keywords: Image watermarking, wavelet transform, Human Visual System, Contrast Sensitivity Function.

Abstract: The efficiency of an image watermarking technique depends on the preservation of visually significant

information. This is attained by embedding the watermark transparently with the maximum possible

strength. The current paper presents an approach for still image digital watermarking in which the

watermark embedding process employs the wavelet transform and incorporates Human Visual System

(HVS) characteristics. The sensitivity of a human observer to contrast with respect to spatial frequency is

described by the Contrast Sensitivity Function (CSF). The strength of the watermark within the

decomposition subbands, which occupy an interval on the spatial frequencies, is adjusted according to this

sensitivity. Moreover, the watermark embedding process is carried over the subband coefficients that lie on

edges where distortions are less noticeable. The experimental evaluation of the proposed method shows very

good results in terms of robustness and transparency.

1 INTRODUCTION

The rapid evolution of multimedia systems and the

wide distribution of digital data over the World

Wide Web addresses the copyright protection of

digital information. The aim is to embed copyright

information, which is called watermark, on digital

data (audio or visual) in order to protect ownership.

In general, a digital watermarking technique must

satisfy two requirements. First, the watermark

should be transparent or perceptually invisible for

image data. The second requirement is that the

watermark should be resistant to attacks that may

remove it or replace it with another watermark. This

implies that the watermark should be robust to

common signal processing operations, such as

compression, filtering, enhancements, rotation,

cropping and translation.

The digital image watermarking techniques in the

literature are typically grouped in two classes: the

spatial domain techniques (Schyndel et al., 1994;

Bender et al., 1996; Wolfgang and Delp, 1996)

which embed the watermark by modifying the pixel

values of the original image and the transform

domain techniques which embed the watermark in

the domain of an invertible transform. The discrete

cosine transform (DCT) and the discrete wavelet

transform (DWT) are commonly used for

watermarking purposes (Swanson et al., 1996; Cox

et al., 1997; Xia et al., 1997; Kim and Moon, 1997;

Dugad et al., 1998; Hsu and Wu, 1999; Wolfgang et

al., 1999; Barni et al., 2001). The transform domain

algorithms modify a subset of the transform

coefficients with the watermarking data and

generally achieve better robustness than spatial

domain methods. Optionally, they may employ a

human visual perception model to weight the

strength of the embedded data. Several research

works employ the wavelet transform because it

presents a number of advantages over the DCT. The

wavelet transform is closer to the human visual

system since it splits the input image into several

frequency bands that can be processed

independently. It is a multi-resolution transform that

permits to locate image features such as smooth

areas, edges or textured areas. Some watermarking

schemes embed watermarking data in textured areas

N. Ellinas J. and E. Manolakis D. (2007).

A ROBUST WATERMARKING SCHEME BASED ON EDGE DETECTION AND CONTRAST SENSITIVITY FUNCTION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 93-100

 SciTePress

or edges where human visual system (HVS) is less

sensitive. Many HVS models have been developed

for quality assessment or image compression (De

Vleeschouwer et al., 2002). Similar visual models

are employed for digital watermarking with a great

success. One model for perceptual watermarking

exploits the contrast sensitivity of the human eye

over the spatial frequency, which is described by the

contrast sensitivity function (CSF), in order to

weight the coefficients of a transform domain.

In this paper, an additive watermarking algorithm

embeds the signature data to selected groups of

wavelet transform coefficients, weighting the

watermark strength according to the CSF sensitivity

of the subband where the corresponding coefficients

reside. The input image is decomposed into four

levels by a DWT, an approximation subband

including the low frequency components and 12

detail subbands including the high frequency

components. Every subband occupies a specific

spatial frequency interval that corresponds to an

average contrast sensitivity factor which is the

weight of the watermark strength. Moreover, the

proposed algorithm detects edges in each subband

and distributes the watermark energy in these

regions, where HVS is less sensitive to. Finally, the

receiver detects the signature data by correlating the

watermarked image with the watermark sequence

and comparing the correlation factor to a threshold

value. The motivation of the present work is to adapt

a watermark sequence to the local image properties

by employing a visual model, providing a

transparent and robust watermark.

2 CSF CHARACTERISTICS

The characteristics of the contrast sensitivity

function in HVS model may be applied on the

coefficients of the detail subbands in the wavelet

decomposition of an image.

2.1 The Contrast Sensitivity Function

Based on the research of the human visual system,

several mathematical models have been devised to

characterize humans’ sensitivity to brightness and

color (Wandell, 1995). The contrast sensitivity

function describes humans’ sensitivity to spatial

frequencies. A model of the CSF for luminance (or

grayscale) images, originally proposed by Mannos

and Sakrison (Mannos and Sakrison, 1994), is given

by:

1.1

)114.0(

)114.0192.0(6.2)(

effCSF

−

(1)

Fig. 1 illustrates the CSF curve which

characterizes the luminance sensitivity of HVS with

respect to spatial frequency. According to this curve,

HVS is less sensitive at very low and very high

frequencies. The properties of CSF may be used to

weight the watermark embedded data so that to be

transparent for a human observer.

Figure 1: Luminance contrast sensitivity function.

2.2 CSF Weighting in DWT Domain

The DWT decomposes a two dimensional image

into subbands using low and high pass filters for the

rows and columns successively. The edge

components of the image are confined within the

high frequency part (detail subbands) whereas the

low frequency part (approximation subband) splits

again until reaching the desired resolution.

Fig.2 shows a four level wavelet decomposition

where each subband is covered by a specific spatial

frequency range. For example, subband HL3 of level

l=3 and orientation θ=1, which describes the vertical

details by indicating the luminance variations along

the horizontal direction, is covered by horizontal

frequencies from 0.125f

max

to 0.25f

fmax

and vertical

frequencies from 0 to 0.125f

max

. The area of the CSF

along the horizontal and vertical directions that

corresponds to the spatial frequency range covered

by this subband is shaded. Therefore, the weighting

for the coefficients of the specific subband must be

estimated by the shaded portions of the CSF

function.

0 5 10 15 20 25 30 35 40 45 5

0.2

0.4

0.6

0.8

1.2

1.4

Relative sensitivity

Spatial frequency (cycles/degree)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

Figure 2: Luminance CSF along horizontal and vertical

directions of four level wavelet decomposition.

3 CSF BASED WATERMARKING

The CSF exploitation in the watermarking process is

accomplished by weighting the coefficients of the

wavelet transform according to the subband they

belong to. The additive embedding algorithm and its

detection at the receiver’s end are analyzed as

follows:

3.1 The Watermark Embedding

Process

Fig. 3 shows the overall process of watermark

insertion. The input image is subjected to a four

level DWT decomposition using the Daubechies 8-

tap filter.

Figure 3: Block diagram of the watermark insertion

process.

The perceptually important wavelet coefficients of

each subband are detected by Sobel edge detector.

To the selected coefficients, the watermark is

inserted in an additive way using (2). The detail

subbands, where the watermark is inserted, contain

edge information or high frequency coefficients.

Consequently, adding the watermark to these

coefficients makes the insertion invisible to the

human visual system. Moreover, the insertion is

weighted according to the sensitivity of the human

visual system to the contrast, which depends on the

spatial frequency.

vuvu

lvuvu

NXwXY

(2)

where

,vu

Y are the modified wavelet coefficients,

,vu

are the edge selected wavelet coefficients,

is a level dependent parameter controlling the

watermark strength,

is the subband visual weight

at level

and orientation

, and

is the

watermark sequence which is represented by

Gaussian noise with zero mean and unit variance.

Fig. 4 illustrates the perceptually significant

wavelet coefficients of the vertical detail subband at

level 2 for “Lena”. The visual weighting factors for

each subband are estimated by averaging the portion

of the CSF curve that corresponds to the high spatial

frequency part. The magnitude of the watermark

strength scale factor is selected for each level of the

wavelet decomposition such that not severely

degrading the watermarked image quality and

considering the fact that the average magnitude of

the coefficients is approximately doubled in each

level from the finest to the coarsest resolution.

Figure 4: Edge coefficients of the vertical orientation

subband at level 2.

DWT

i,j

u,v

edge

detector

watermark

insertion

IDWT

u,v

i,j

CSF

weighting

u,v

Vertical detail

LH1 - è=1

Diagonal detail

HH1 - è=2

Horizontal detail

HL1 - è=3

è=0

max

horizontal

vertical

LH2

HH2HL2

LH3

HH3HL3

A ROBUST WATERMARKING SCHEME BASED ON EDGE DETECTION AND CONTRAST SENSITIVITY

FUNCTION

3.2 The Watermark Detection Process

The possibly distorted watermark sequence is

detected by combining the original image

with

the possibly distorted watermarked image

reversing the steps of the insertion process, as Fig. 5

shows.

Figure 5: Block diagram of the watermark detection

process.

The extraction process is performed by

subtracting the original perceptual significant

coefficients from the corresponding received

watermarked coefficients (which may have been

attacked and distorted) and scaling the difference by

the weighting and watermark strength factors. The

watermark detection is accomplished without

referring to the original image, considering the

correlation between the watermarked coefficients

and the watermarking sequence (Barni et al., 2001):

∑∑

−

vuvu

(3)

where

,vu

Y represents the watermarked perceptually

significant coefficients and

is the watermark

sequence.

The correlation factor is compared to a threshold

value, as in (4)

watermarkfalseT

watermarktrueT

〈

〉

(4)

where

297.3

(5)

Variance

is defined as

()

)(

∑∑

−

ΜΝ

(6)

3.3 Image Quality Assessment

The objective evaluation of image quality is

performed by the PSNR, which is defined as

⎟

⎠

⎞

⎜

⎝

⎛

mse

PSNR

255255

log10

(7)

where

mse is the mean square error:

[]

),(),(

∑∑

−

−=

jiyjix

mse

(8)

where

are the dimensions of the input image

and

, are the original and the watermarked

images.

However, PSNR declines from the perceived

subjective quality because the HVS does not

correlate well with the square of the error. For this

reason, the weighted PSNR that takes into account

the local variance is also used as follows:

⎟

⎠

⎞

⎜

⎝

⎛

wmse

wPSNR

255255

log10

(9)

where

),var(1

),(),(1

∑∑

−

⎥

⎦

⎤

⎢

⎣

⎡

−

jiyjix

wmse

(10)

4 EXPERIMENTAL RESULTS

The proposed method is evaluated in four images:

“Lena”, which is an image with large smooth

regions, “Barbara”, “Baboon” and “Boat”, which

have textured regions. The size of all images is

512×512 pixels. The performance measures are the

invisibility of the inserted watermark and the

robustness of the method against various types of

attacks. The attacks employed for testing are JPEG

compression, median filtering, Gaussian noise and

cropping.

DWT

i,j

u,v

edge

detector

similarity

measure

u,v

i,j

decision

threshold

u,v

DWT

CSF

weighting

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

(a) (b)

Figure 6: (a) Original image; (b) Watermarked image.

Fig. 6 shows the original image of “Lena” and its

watermarked copy whereas Fig. 7 shows their

difference. It is obvious that the watermarked copy

is undistinguishable from the original image. In the

difference, which is suitably scaled for display, it is

evident that most of the watermark data are added to

the edges where they are perceptually invisible.

Figure 7: Scaled difference between original and

watermarked images.

Table 1 depicts the objective quality values of

the proposed method for the tested images. These

values are obtained setting the watermark strength

factor to a low value so that the detector response is

just over the threshold value. It is well known that

the two desirable features of watermarking,

invisibility and robustness, are contradictory. Thus,

the values of the watermark strength factor

are

properly tuned so that the watermarking sequence is

completely invisible although robustness is at a

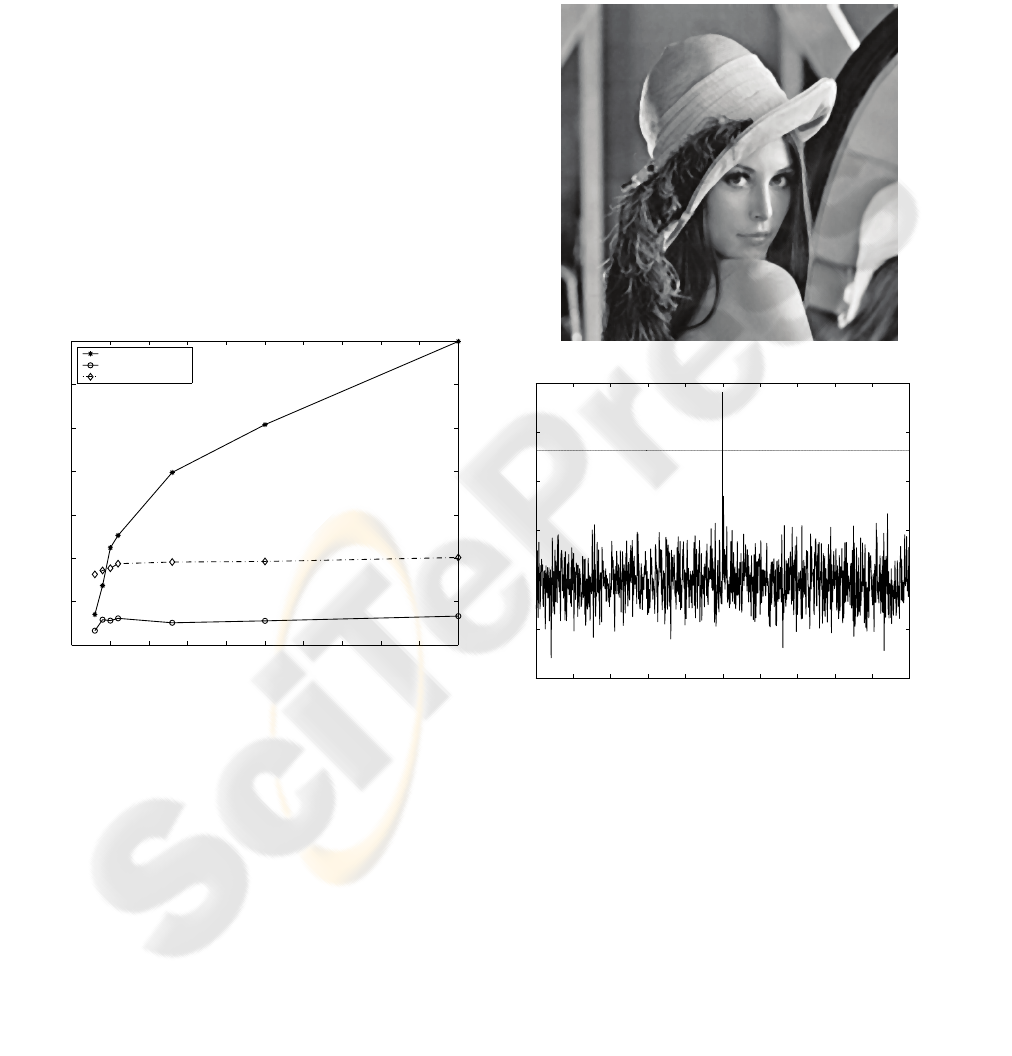
medium level. Fig. 8 shows the response of the

watermark detector to 1000 randomly generated

watermarks, with the original watermark placed in

the middle. In this case, the watermark strength is

such that the watermark sequence is robust enough

and the objective quality of the watermarked image

is just above 35 dB, which is a typical value just

before image is degrading.

Table 1: PSNR and wPSNR values of watermarked test

images.

Images

PSNR

(dB)

wPSNR

(dB)

Lena 45.18 65.66

Barbara 44 64.21

Baboon 42.65 61.95

Boat 44.45 63.67

Figure 8: Response of watermark detector for “Lena”.

Table 2 shows the effectiveness of the proposed

scheme against two other typical algorithms on

wavelet-based watermarking (Dugad et al., 1998;

Kim and Moon, 1999). The first method employs a

unique threshold value over all the detail subbands

for embedding the signature data, whereas the

second method uses level adaptive thresholding for

more accurate estimation of edge coefficients.

Table 2: PSNR and detector response values of three

watermarking schemes for the test image “Lena”.

Algorithms

PSNR

(dB)

Detector

response

Proposed 35.11

53.76

Dugad et al. 35.73 28.20

Kim and Moon 35.18 43.60

The proposed scheme outperforms significantly

over the other two methods for about the same

objective quality of the watermarked image. This

robust performance lies on the fact that watermark

data are placed exactly on the detected edges where

HVS is less sensitive to distortions. The threshold

values employed by the other algorithms can not

0 100 200 300 400 500 600 700 800 900 100

−10

Watermarks

Detector response

A ROBUST WATERMARKING SCHEME BASED ON EDGE DETECTION AND CONTRAST SENSITIVITY

FUNCTION

exactly locate the edges on the wavelet domain and

for that reason some watermark data are placed on

coefficients that affect the quality of the image.

Moreover, in the proposed method there are no

threshold values that are image dependent and their

tuning to optimum values is a serious drawback.

To appreciate the robustness of the proposed

method against several common attacks, the

following experiments were performed in “Lena”

image.

Firstly, JPEG coding with variable quality factor

was applied to the watermarked image and 1000

watermarks were inserted for examining the

detector’s response about their presence. In Fig. 9,

the response of the detector to the embedded

watermark is plotted against the JPEG quality factor.

Also, the detection threshold and the second highest

response are shown. The detector response remains

above threshold up to a quality factor of 5 whereas

the second highest response remains always under

the threshold value. This proves the robustness of

the proposed method against JPEG compression.

Figure 9: Detector response versus JPEG quality factor.

Fig. 10(a) illustrates the watermarked image

after median filtering with a window size of 3×3

whereas Fig. 10(b) shows the detector response to

this kind of attack. Comparing this figure with Fig.

8, we observe that correlation factor decreases to

about one third of its initial value because of median

filtering. This may be explained since median

filtering smoothes the edges of an image where

nearly all of the watermarking data have been

embedded.

The proposed method is quite immune to

Gaussian noise, as Fig. 11 shows. Fig. 11(a) presents

the watermarked copy which has been contaminated

with Gaussian noise of zero mean and variance of 20

whereas Fig. 11(b) shows the detector response. The

output of the detector is slightly lower than that of

Fig. 8, where no attack is involved.

Finally, the robustness of the proposed

watermarking method against cropping is examined.

When the watermarked image is cropped, part of the

embedded information is discarded making the

detection more elaborate.

(a)

(b)

Figure 10: (a) Watermarked copy after median filtering;

(b) Detector response of the attacked watermarked image.

Thus, it is important the watermark method to

spread the information all over the image so that, if

possible, any remaining part to include enough

information for the watermark recovery. Our

experiment on cropping is to examine the resilience

of the watermark after the removal of a substantial

part of the original image. Fig. 12(a) shows the

cropped watermarked image which is half of the

original image. The ability of the decoder to trace

the watermark of the sub-image is shown in Fig.

0 5 10 15 20 25 30 35 40 45 5

Quality factor

Detector response

inserted watermark

second highest peak

threshold level

0 100 200 300 400 500 600 700 800 900 100

−10

−5

Watermarks

Detector response

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

12(b). It is quite impressive that the detector

response is well above threshold, revealing the

robustness of the proposed method. The watermark

sequence is hidden on the wavelet coefficients that

reside on the detail subbands or on the edges which

exist all over the input image. The proposed method

may be less effective when the remaining part

contains mainly smooth areas where the embedded

information is less, but this is difficult to be

accomplished.

(a)

(b)

Figure 11: (a) Watermarked copy after Gaussian noise; (b)

Detector response of the attacked watermarked image.

(a)

(b)

Figure 12: (a) Cropped watermarked copy; (b) Detector

response of the cropped watermarked image.

5 CONCLUSIONS

In this paper, a novel method for image

watermarking has been presented. The method

embeds the watermarking data on selected wavelet

coefficients of the input image considering the CSF

characteristics of the HVS. The selected coefficients

reside on the detail subbands and describe the edges

of the image. Thus, exploiting the HVS which is less

sensitive to alterations on high frequencies, the

embedded information becomes invisible. The

evaluation of the proposed method shows very good

performance as far as invisibility and robustness is

concerned. The proposed scheme behaves very well

in various common signal processing methods as

compression, filtering, noise and cropping.

0 100 200 300 400 500 600 700 800 900 100

−10

−5

Watermarks

Detector response

0 100 200 300 400 500 600 700 800 900 100

−10

−5

Watermarks

Detector response

A ROBUST WATERMARKING SCHEME BASED ON EDGE DETECTION AND CONTRAST SENSITIVITY

FUNCTION

ACKNOWLEDGEMENTS

The project is co-funded by the European Social

Fund and National Resources-EPEAEK II-

ARCHIMEDES granted to Technological Education

Institute of Thessaloniki under program number 10.

REFERENCES

Schyndel, R., Tirkel, A. and Osborne, C., 1994. A digital

watermark. In IEEE Proc. of International Conference

on Image Processing 1994.

Bender, W., Gruhl, D., Morimoto, N. and Lu, A., 1996.

Techniques for data hiding. In IBM Systems Journal,

35(3-4).

Wolfgang, R. B. and Delp, E. J., 1996. A watermark for

digital images,” In IEEE Proc. of International

Conference on Image Processing 1996.

Swanson, M. D., Zhu, B. and Tewfik, A. H., 1996.

Transparent robust image watermarking. In IEEE

Proc. of International Conference on Image

Processing 1996.

Cox, I. J., Kilian, J., Leighton, T. and Shamoon, T., 1997.

Secure spread spectrum watermarking for multimedia.

In IEEE Transactions on Image Processing, 6(12).

Barni, M., Bartolini, F. and Piva, A., 2001. Improved

wavelet-based watermarking through pixel-wise

masking. In IEEE Transactions on Image Processing,

10(5).

Xia, X., Boncelet, C. G. and Arce, G. R., 1997. A

multiresolution watermark for digital images. In IEEE

Proc. of International Conference on Image

Processing 1997.

Kim, J. R. and Moon, Y. S., 1999. A robust wavelet-based

digital watermarking using level-adaptive

thresholding. In IEEE Proc. of International

Conference on Image Processing 1999.

Hsu, C. T. and Wu, J. L., 1999. Hidden digital watermarks

in images. In IEEE Transactions on Image Processing,

8(1).

Dugad, R., Ratakonda, K. and Ahuja, N., 1998. A new

wavelet-based scheme for watermarking images. In

IEEE Proc. of International Conference on Image

Processing 1998.

Wolfgang, R. B., Podilchuk, C. I. and Delp, E. J., 1999.

Perceptual watermarks for digital images and video. In

SPIE Proc. of International Conference on Security

and watermarking of multimedia contents 1999.

De Vleeschouwer, C., Delaigle, J. F. and Macq, B., 2002.

Invisibility and application functionalities in

perceptual watermarking an overview. In IEEE Proc.,

90(1).

Wandell, B. A., 1995. Foundations of Vision, Sinauer

Associates Inc., Sunderland MA.

Mannos, J. and Sakrison, D., 1974. The effects of a visual

fidelity criterionon the encoding of images. In IEEE

Transactions on Information Theory, 20.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

100