ENERGY MINIMIZATION APPROACH FOR ONLINE DATA

ASSOCIATION WITH MISSING DATA

Abir El Abed, S

everine Dubuisson and Dominique B

eziat

Laboratoire d’Informatique de Paris 6, Universit

e Pierre et Marie Curie

104 avenue du Pr

esident Kennedy, 75016 Paris, France

Keywords:

Online data association, energy minimization, prior informationless and non-rigid motion.

Abstract:

Data association problem is of crucial importance to improve online target tracking performance in many

difﬁcult visual environments. Usually, association effectiveness is based on prior information and observation

category. However, some problems can arise when targets are quite similar. Therefore, neither the color

nor the shape could be helpful informations to achieve the task of data association. Likewise, problems can

also arise when tracking deformable targets, under the constraint of missing data, with complex motions. Such

restriction, i.e. the lack in prior information, limit the association performance. To remedy, we propose a novel

method for data association, inspired from the evolution of the target dynamic model, and based on a global

minimization of an energy vector. The main idea is to measure the absolute geometric accuracy between

features. Its parameterless constitutes the main advantage of our energy minimization approach. Only one

information, the position, is used as input to our algorithm. We have tested our approach on several sequences

to show its effectiveness.

1 INTRODUCTION

Traditionally, multiple object tracking deals with the

state estimation of moving targets. A track is a state

trajectory estimated from the available measurements

that have been associated with the same target (Ver-

maak et al., 2005). The main difﬁculty comes from

the assignment of a given measurement to a target

model. These assignments are generally unknown, as

are the true target models. The idea of data associa-

tion remains to ﬁnd a partition of observations such

that each element is generated by a target, or clut-

ter, whose statistical properties differ from one tar-

get to another. The literature contains some classical

approaches: we can distinguish the deterministic ap-

proaches from the probabilistic ones.

Deterministic approaches select the best of several

candidate associations, without taking into account its

context correctness, by using a score function (Ver-

maak et al., 2005). The simplest deterministic method

for data association is the Nearest-Neighbor Standard

Filter (NNSF) (Rong and Bar-Shalom, 1996) that se-

lects the closest validate measurement to a predicted

target and uses it for its state estimation. Usually,

the distance measure used is the Mahalanobis one.

Since the ﬁlter does not take into account the pos-

sibility of incorrect associations, the performance of

this ﬁlter might be poor in some cases, resulting in an

incorrect association between measurements and tar-

gets. In some tracking applications, the color is also

exploited for the problem of data association. One

can measure the color histogram difference between

a measurement and the objects of the previous frame

using the histogram intersection technique. Unfortu-

nately, the color metric is not sufﬁcient for a correct

data association in many cases: for deformable ob-

jects, which color distribution may differ from one

frame to another, or in case of several quite identi-

cal objects.

Probabilistic approaches are based on posterior prob-

ability and make an association decision using the

probability error (Rasmussen and Hager, 2001).

Among probabilistic approaches, we can cite the most

general one, called Multiple Hypothesis Tracking

(MHT) (Vermaak et al., 2005). In MHT, the multiple

hypotheses are formed and propagated, implying the

371

El Abed A., Dubuisson S. and Béréziat D. (2007).

ENERGY MINIMIZATION APPROACH FOR ONLINE DATA ASSOCIATION WITH MISSING DATA.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 371-378

 SciTePress

calculation of every possible hypothesis. Due to the

exploring of a high-dimensional joint state space, this

method is computational intensive. Another strategy

for multiple target tracking association is the Prob-

ability Data Association Filter (PDAF) (Rasmussen

and Hager, 2001), that assigns an association proba-

bility to each measurement and uses these probabili-

ties to weight the measurements for track update. The

original PDAF formulation has some limitations: it

assumes that all measurements come from the track

being updated, that is not true in case of dense tar-

get conditions. The Joint Probability Data Associa-

tion (JPDA) (Fortmann et al., 1983) uses a weighted

sum of all measurements near the predicted state, each

weight corresponding to the posterior probability for

a measurement to come from a target. JPDAF pro-

vides an optimal data solution in the Bayesian frame-

work. However, the number of possible hypothesis

increases rapidly with the number of targets, requir-

ing prohibitive amount of time calculating.

Generally, an effective data association method is

based on prior information and observation category.

If we have a lack of prior information, that can hap-

pen when the observer has no information concern-

ing the system, the association task becomes difﬁcult.

Such cases can occur when the observed system is de-

formable, moreover, when we observe, with minor in-

formation about the movement, multiple objects that

are quite similar even non distinguishable. It can be

more complicated if we have a considerable interval

of time between observations and if the observer has

no prior information about object’s motion. Likewise,

if we only observe target positions, we can face a mea-

surement that is equidistant from several targets: all

target association probabilities are relatively the same

and it is difﬁcult to associate the good measurement

with the good target. As far as, no association method

can handle all the cases illustrated previously.

In this paper, we propose a novel method for data

association based on the minimization of an energy

magnitude k

Ek and adapted to the circumstances de-

scribed previously. This energy, inspired from tar-

get motion, measures the geometric accuracy between

features and associates the measurement y (given by

sensor) with the target k if k(

)

k is minimized. The

main advantages of this energy are followed. It does

not require parameters or prior knowledge and is not

a time-consumer. Exclusively one information about

targets is used: positions. Besides, it can handle

the problem of association when a measurement falls

within the validation region for several targets and is

equidistant from them.

The outline of this paper is as follows. In Section 2,

we expose our energy minimization approach, de-

rive its geometrical representation and its mathemat-

ical model. The proposed method is then evaluated

and tested on several sequences in Section 3. Finally,

concluding remarks and perspective are given in Sec-

tion 4.

2 ENERGY MINIMIZATION

APPROACH FOR DATA

ASSOCIATION

We ﬁrst need to deﬁne some terms that will be often

used in this paper. We dispose a video sequence de-

scribing a dynamical scene. It is observed by a set

of sensors. Each observation contains at least one

measurement: a position. The number of available

measurements can differ from one observation to an-

other. Each measurement can be associated with a

speciﬁc object in the scene (i.e. target), or can be

a false alarm. At a speciﬁc time t, observations are

assumed to be available from N

obs

sensors. The set

of observations coming from all sensors is given by

y = (y

,...,y

obs

), where y

= (y

,...,y

) is the vector

containing the M

measurements coming from the i

sensor, also called observation. We suppose that each

sensor can generate at most one observation, contain-

ing at least one measurement at a particular time step

and that the number of measurements delivered by

the sensors varies with time. When an observation

is available, our goal is to associate a maximum one

measurement per target. The total number of targets

is K.

2.1 Energy Minimization Modelling

Generally, an effective data association method is

based on measurement category. When the measure-

ment is limited to a position, and falls inside the vali-

dation region of several targets and is equidistant from

them (see Figure 1.a), it will be associated with all

these targets if we use the NNSF or Monte Carlo

JPDAF approaches. As well as, in multiple target

tracking, feature targets can be quite similar. Accord-

ingly, even if information about their color distribu-

tion or shape is available, the association task is difﬁ-

cult under such assumptions or impossible in case of

complex dynamics.

In this paper, we propose an algorithm for data as-

sociation restricted to one category of measurement:

the position. Furthermore, we afﬁrm the total lack of

prior information concerning targets: exclusively the

two anterior predicted positions are used. We will ﬁrst

give the concept of our approach before starting its

mathematical modeling. Our intention is to formalize

a method able to associate a measurement according

to the restrictions displayed in Section 1. We deﬁne

a novel energy vector

E in the direct afﬁne euclidean

space (O,

k). This energy is inspired from the tar-

get’s dynamic evolution. The dynamic model is de-

scribed in terms of displacements in the target space

(x,y). If we only consider the linear translation in one

direction, the problem of data association is limited to

the computation of the Mahalanobis distance energy

(see after for details). Thus, in case of complex dy-

namics such as non linear displacements, oscillatory

motions and non-constant velocities, we are vis-a-vis

a problem because

will be an insufﬁcient infor-

mative source. To remedy, we incorporate a second

energy term

which measures the absolute accu-

racy between the dynamic features and indicates how

much their parameters are close. Moreover, we dis-

tinguish some dynamic cases, that will be clariﬁed by

geometric descriptions afterward, for whose we need

to compensate

by the proximity energy evolution

for a better association of te available data.

The energy vector

E is only computed when the mea-

surement falls within several validation regions. We

consider a measurement as a clutter if it is not in-

cluded in any validation region. In our case, the val-

idation region is an ellipsoid that contains a given

probability mass under the Gaussian assumption. The

minor and major axes of this ellipsoid are respec-

tively given by the largest and smallest eigenvalues

of the covariance matrix, their directions are given by

the corresponding eigenvectors, and the center is the

mean of the target.

We deﬁne the energy vector between the k

target

(k = 1, . . . , K) and the measurement y

, i.e. j

mea-

surement of the i

sensor, by:

(

)

√

∑

l=1

(

)

(1)

where α

∑

k=1

||(

)

is a weighted factor intro-

duced to sensibly emphasize the relative importance

attached to the energy quantities

Before interpreting each energy, we consider a target

A and a measurement y

. Besides, we call (see Fig-

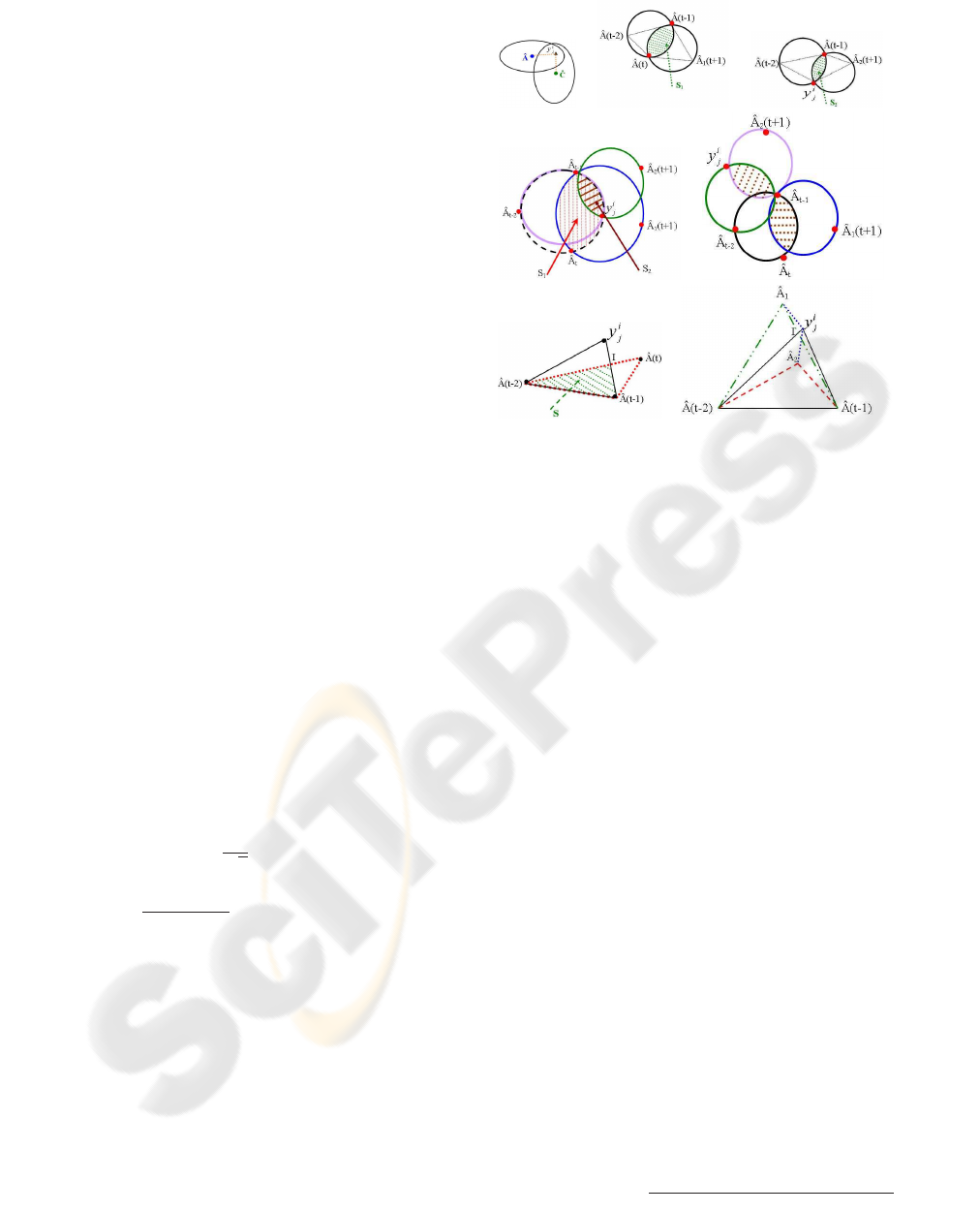
ure 1 for illustration):

•

A(t −2),

A(t −1),

A(t) and

(t + 1): prediction of A

at t −2, t −1, t and t + 1 by using the initial dynamic

model;

•

(t + 1): prediction of A at t + 1 by using the updated

dynamic model. In this case, the measurement y

is as-

sociated with the target A at instant t and the parameters

of the dynamic model are updated according to y

(a) (b) (c)

(d) (e)

(f) (g)

Figure 1: (a) Measurement y

falls inside the two val-

idation regions of A and C; (b-c-f) Intersection surfaces

,S}; (d-e) Difference between the sufaces S

and

extracted from two dynamical models; (g) Intersection

surfaces where two predictions at instant t,

and

, are

equidistant from y

Prediction is based on the use of a dynamic model

which parameters are generally ﬁxed by learning from

a training sequence to represent plausible motions

such as constant velocities or critically damped os-

cillations (North et al., 2000; Blake and Isard, 1998).

For complex dynamics, such as non-constant veloc-

ities or non-periodic oscillations, the choice of the

parameters for an estimation algorithm is difﬁcult.

Furthermore, the learning step becomes particularly

more difﬁcult in the case of missing data, because the

dynamic between two successive observations is un-

known. For these reasons, the parameters of our dy-

namic model are set in an adaptive and automated way

once a measurement is available (Abed et al., 2006).

The energy vector (

)

contains three components,

{

}, as deﬁned below:

1. The Mahalanobis distance energy, (

)

, mea-

sures the distance between a measurement y

oc-

curred at instant t and the prediction of the target

A at t −1. This energy is sufﬁcient to associate

the available measurement if the target’s motion

is limited to translations in one direction (case of

linear displacements). It is given by:

(

)

= k(

)

i (2)

−

A(t −1))

−1

−

A(t −1))

where Σ

is the covariance matrix of the k

target

(we designe the k

target by A in the equation).

2. To consider the case of complex dynamics, such

as oscillatory motions or non-constant velocities,

we have added the absolute accuracy evolution

energy (

)

. It introduces the notion of the

geometric accuracy between two sets of features

whose dynamic evolution is different. The de-

scription of both models are followed:

• The updated dynamic model set considers that the

available measurement y

at t is generated by the

target and updates the parameters of its dynamic

model to predict the new state of the target k at t + 1;

• The not updated dynamic model set predicts the new

state at t + 1 without considering the presence of the

measurement, i.e. without updating the parameters

of the dynamic model.

(

)

extends a numerical estimation of the

closeness between two dynamic models. Our

idea aims to evaluate the parameters of the dy-

namic model in two cases if the measurement

arises from this target or no. We ﬁrst pre-

dict the states

(t + 1) and

(t + 1) of the tar-

get at t + 1. We then determine S

, the intersec-

tion surface between the two circumscribed cir-

cles of the triangles (

A(t −2),

A(t −1),

A(t)) and

(

A(t −1),

A(t),

(t + 1)), and S

, the intersection

surface between the two circumscribed circles of

the triangles (

A(t − 2),

A(t − 1), y

) and (

A(t −

1),y

(t + 1)), (see Figures( 1.b-c)). (

)

minimized when the similarity between both dy-

namic models is maximized and is given by:

(

)

= k(

)

j = |S

−S

j (3)

We compare these two sets to measure the ratio of

similarity, deﬁned by R

= 1−k(

)

k, between

the predictions at t + 1 given by two different dy-

namic models for target k. Increasing this ratio

maximizes the probability that the measurement

is generated by target k and the resemblance

between two dynamic models.

A question might be asked: is the component

able to handle all type of motions ?

Indeed,

evaluates a numerical measure of sim-

ilarity between dynamic models. This measure-

ment depends on the difference between two sur-

faces. It is considered as reliable if both positions,

A(t) and y

, are on the same side comparing to

axis (

t−2

t−1

), see Figure 1.d. In Figure 1.e, we

show the case where both surfaces, S

and S

, are

quite similar, which imply

to be null. This case

can occur when the positions of

A(t) and y

are

diametrically opposite or when their positions are

in different side comparing to axis (

t−2

t−1

). In

such cases, the energy

is not a sufﬁcient infor-

mative source to achieve the task of association.

To compensate this energy, we then incorporate

the third energy

3. The proximity energy evolution, (

)

, is the in-

verse of the surface S deﬁned by the common area

between the two triangles (

A(t −2),

A(t −1),y

)

and (

A(t −2),

A(t −1),

A(t)) (see the dotted area

of Figure 1.f). This energy evaluates the abso-

lute accuracy between the prediction

A(t) and the

measurement y

at instant t. Increasing S means

that the prediction and measurement at instant t

are close. This energy is given by:

(

)

= k(

)

k =

k (4)

Another question could be asked: why do we have

to use the intersection surface instead of only cal-

culating the distance between the measurement y

and the prediction of target’s position at instant t?

In Figure 1.g, we have two predictions at instant

and

. They are both equidistant from the

measurement y

. If we only compute the distance

to measure the proximity energy, we will get that

both models have the same degree of similarity

with the initiation model deﬁned by the dynamic

model of points (

A(t −2),

A(t −1),y

). This re-

sult leads to a contradiction with the reality. This

problem can be explained by the fact that if they

have both the same degree of similarity with the

third dynamic model, we can conclude that their

corresponding targets have the same dynamic. For

this reason, we have chosen to evaluate the sim-

ilarity by extracting the intersection surface be-

tween triangles. We can remark in Figure 1.g

that these intersection surfaces are very different,

which leads to a different measure in the degree

of similarity.

Finally, the measurement y

is associated with the tar-

get k if its energy magnitude is minimized:

→k



min

k=1,...,K

(k(

)



(5)







min

k=1,...,K





√

∑

l=1

)











with 0 ≤ α

≤ 1 and 0 ≤ k(

)

k ≤ 1.

We have described a novel approach for data associ-

ation based on the minimization of an energy magni-

tude whose components are extracted from geomet-

rical representations (area and distance) constructed

with measurements, previous states and predictions.

The purpose of choosing a geometrical deﬁnition for

these energies refers to:

• show the geometrical continuity of the system between

predictions and previous states using two different dy-

namic models;

• measure the similarity between predictions, at a partic-

ular time for the same object, using two different dy-

namic models, that logically must be quite similar be-

cause they represent the same system.

3 EXPERIMENTAL RESULTS

3.1 Synthetic Test

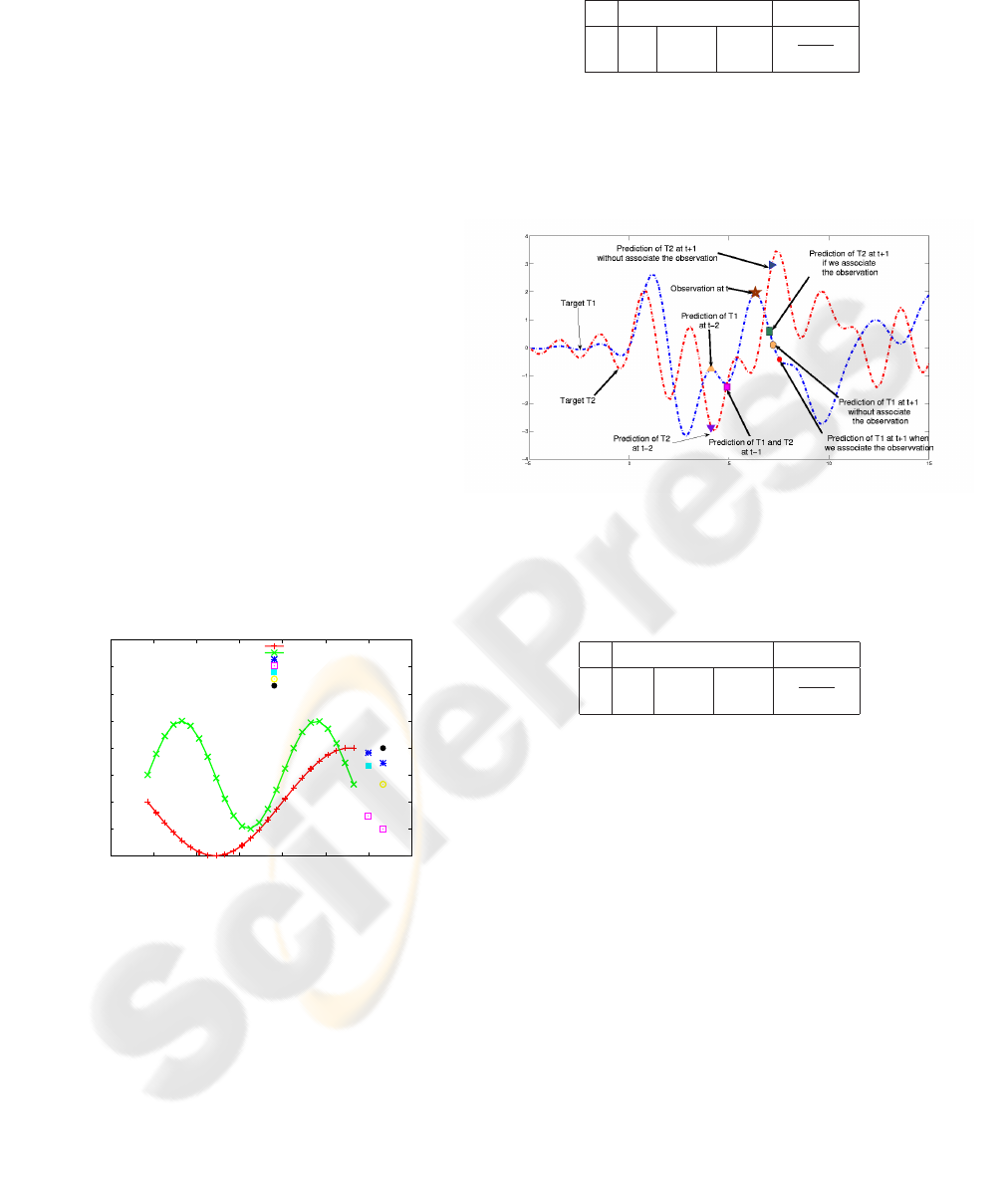
To expose the performance of our energy minimiza-

tion approach, we suggest the synthetic example of

Figure 2, which explores the case of an oscillatory

motion with a constant phase. It shows two targets T

and T

whose dynamic models are deﬁned by two dif-

ferent sinusoids, sin(x) and sin(2x) + 0.5. The mea-

surement y (full square in Figure 2), is equidistant

from both targets and falls in their validation regions.

In such case, both targets are candidates to be associ-

ated with this measurement. We compute the energy

magnitude for each target (see Table 1) and obtain that

)

k< k(

)

kand the measurement is associated

with T

-1

-0.5

0.5

1.5

2.5

-4 -3 -2 -1 0 1 2 3

Prediction without observation for T1

Prediction without observation for T2

Observation at instant t

Prediction with observation for T1

Prediction with observation for T2

Figure 2: Sinusoids with a constant phase: the dotted lines

represent the trajectories of targets T

and T

. The full

square is the measurement y. The dotted squares and blue

stars are the predictions of T

and T

at instants {t +1,t+2}

without taking into account the presence of the observation.

The dotted and full circles are the predictions of T

and T

if we consider that the observation is associated with both

targets.

We give another example where the motion of both

targets is given by a sinusoid with a non periodic

phase, see Figure 3. At instant t −1, both targets

have the same position as shown in Figure 3. If we

use the NNSF method, the measurement will be as-

sociated with both targets since it is equidistant from

Table 1: Energy magnitude computation for targets T

and

k α

)

k k(

)

1 0.5 0.0001 0.4821 0.5278

2 0.5 0.9999 0.5179 0.9362

them. To improve the association result, we compute

the energy magnitude for each target and the results

are given in Table 2. We obtain k(

)

k < k(

)

and the measurement is associated with T

Figure 3: Sinusoids with non-constant phases: the dot-

ted lines represent the trajectories of targets; the shapes

(squares, circles, triangles) are their predictions at different

instants.

Table 2: Energy magnitude computation for T

and T

k α

)

k k(

)

1 0.5 0.0970 0.3094 0.3441

2 0.5 0.9030 0.6906 0.7170

3.2 Van-Plane Test

In the following experiment, the available observa-

tion at instant t contains two measurements M

and

, each one represents a position in the target space

(x,y). The ﬁrst row in Figure 4 contains the frames

at {t −2,t −1,t} where two targets {T

}, the van

and the plane, are present. If we look at the position

of these measurements on the real frame at t (right

image in Figure 4), we observe that M

is closed to T

and M

to T

. In the second and third rows, we show

the predictions of both targets by evaluating two dif-

ferent dynamic models in the target space (x, y). We

point out that the horizontal and the vertical axis of the

frame are represented by the y-axis and x-axis in the

target space. We can remark that the distance from

to M

is larger than the one from T

to M

, see

the Mahalanobis distance energy α

)

}

k in

Table 3. Hence, if we use the Nearest Neighbor as-

sociation method, the target T

will be associated to

which causes a contradiction with the reality. To

remedy, we compute the energies

and

which

compensate the insufﬁciency of

. Using the energy

minimization approach, we obtain that the energies

magnitudes are minimized when M

and M

are re-

spectively associated with targets T

and T

(see Ta-

ble 3).

Figure 4: Van Plane test. In the ﬁrst row: left and middle

images represent the frames at {t −2,t −1} where two tar-

gets {T

} are present; right image is the real frame at t.

The available observation at t contains two measurements

}. In the second and third rows, we show the posi-

tion of both targets at different instants.

Table 3: Energy magnitude computation for both tar-

gets when the measurements {M

} are associated with

them.

k α

)

k k(

)

1 0.3141 0.02 0.3429 0.2687

2 0.6858 0.98 0.6571 0.7879

k α

)

1 0.3179 0.7236 0.8636 0.6759

2 0.6821 0.2764 0.1364 0.4322

3.3 Walking Men Test

The ”Walking men” sequence shows: Figure 5.a three

men walking close at intant (t −2), Figure 5.b, at t −

1, two men (T

and T

) continue walking in the same

direction, while the third one (T

) takes the opposite

direction.

The available observation at t contains three measure-

ments corresponding to positions in the target space

a b

c d

Figure 5: Walking men test. (a) Frame at (t −2): three

walking men close one to the other; (b) Frame at t − 1:

two men continue walking in the same direction and the

third one takes the opposite direction; (c) The observation

at t: two men cross and we have a partial occlusion between

them; (d) Frame at t + 1: the cross men change their direc-

tions.

Table 4: Energy magnitude computation for targets k when

measurements M

are associated with them.

k α

)

k k(

)

1 0.144 0.03 0 0.085

2 0.411 0.82 0 0.53

3 0.444 0.16 0 0.47

k α

)

1 0.70 0.16 0.5 0.51

2 0.15 0.22 0.5 0.32

3 0.15 0.62 0 0.37

k α

)

k k(

)

1 0.63 0.0037 0 0.363

2 0.21 0.76 0 0.455

3 0.16 0.235 0 0.16

(x,y). In Figure 5.c, we show the corresponding

frame at instant t where we observe a partial occlu-

sion between two walking men. We have put the mea-

surements in Table 4 in a way that the measurement

is generated by the target T

. We notice that the

observed positions of the cross men are very close.

Figure 5.d represents the real frame at instant t + 1

where we remark that the cross men change their

directions. We remark from Table 4 that the mea-

surement M

is equidistant from targets T

and T

(α

)

k= α

)

k= 0.15). We also remark

from Table 4 that most of time the third energy is null,

this effect is due to the presence of a linear movement

(motion limited to a displacement in two directions

x and y). Once the energies are computed, we obtain

the energy magnitude k(

)kis minimized when mea-

surement M

is associated to target T

, see the column

of k(

)

k in Table 4. Despite the change in illumi-

nation, the measurements were correctly associated to

targets by using the approach of energy minimization.

3.4 Window Men Test

In this sequence we observe, at instant t −2, two tar-

gets: the ﬁrst one is static and the second undergoes a

linear movement (see Figure 6.a). At instant t −1,

only the second target continues walking and goes

near to the ﬁrst one, Figure 6.b. At instant t, an ob-

servation containing two measurements, containing

positions, is available. Notice that the observed po-

sitions are close and there is a partial occlusion be-

tween both targets. Table 5 shows that the distance

from measurement M

to target T

is less than the dis-

tance from M

to T

, k(

)

k < k(

)

k, which

leads to a contradiction with the reality. We compute

the second energy to compensate the ﬁrst one. The

third energy is null due to the linear displacement of

both targets. As we can remark from Table 5, the

energy magnitude k(

)

k and k(

)

k are mini-

mized when M

and M

are associated with T

and T

respectively. We remark that our approach of energy

minimization gives a correct association despite the

presence of a light reﬂexion on the window.

a b

c d

Figure 6: Window men test. (a) Frame at t −2: two targets

are present; (b) Frame at t −1: both targets are close; (c) the

available observation at t; (d) Frame at intant t: both targets

move.

Table 5: Energy magnitude computation for targets k when

measurements M

are associated with them.

k k(

)

k α

)

k k(

)

1 0 0 0 0 0 0 0

2 0.0607 6.2 0 1 1 0 0.82

k k(

)

k α

)

k k(

)

1 0.0217 0.36 0 0.3 0.83 0 0.51

2 0.0518 0.07 0 0.7 0.16 0 0.42

3.5 Ant Sequence Test

We have tested our method on another sequence

showing ants having complex motions. They move

with a non-constant velocity and can accelerate,

decelerate and sometimes stop moving or starting.

These ants are quite similar even non-distinguishable

and characterized by the same gray level distribu-

tion. The sensor, at instant t, provides an observa-

tion containing six measurements corresponding to

positions in the (x,y) space. In such scene, only

one information can be used: the motion. We re-

mark from Figure 7 that their displacement is erratic.

The ants change their direction, accelerate, deceler-

ate, stop moving, do rotation around their axis, etc.

Figure 7.(a-b) are the acquisitions at instant t −2 and

t−1 and represents the frames 10 and 25 of the ant se-

quence. We remark there is a considerable interval of

time between these two frames. We have labeled the

ants just to show their displacements from one frame

to another. Figure 7.c shows the available observation

at t and represents the frame 35 of the sequence. Fig-

ure 7.d is the real frame at t + 1. Table 6 contains the

numerical values of all energies computed between

measurements and targets. We have multiplied each

one by 100 to show clearly the difference between

them. We have also ﬁxed the order of classiﬁcation in

Table 6 so that the measurement M

is provided from

target T

. If we use the Nearest Neighbor ﬁlter to as-

sociate the available observations, the measurements

}will be respectively associated with tar-

gets {T

} which leads to a contradiction with

the reality (see the energy α

)

k in Table 6).

To remedy, we associate our observations by using

the energy minimization approach. We remark from

Table 6 that the energies α

)

k < α

)

and α

)

k < α

)

k which compensates

the error given by α

)

k. Finally, the follow-

ing result is obtained: k(

)

k is minimized when

is associated with target T

. We recite that a mea-

surement is associated with a target if the magnitude

of its energy is minimal (equation 5). Lets take an-

other example to show the necessity of using the en-

ergy

in our formulation to compensate the oth-

ers one. If we only use the energies α

)

k and

)

k to associate data, we will get the follow-

ing result: k(

)

k < k(

)

k and the measure-

ment M

will be associated with target T

which leads

to an error in association. We can remark from Ta-

ble 6 that α

)

k< α

)

k which compen-

sate the other energies. Finally, we observe that each

measurement is well associated with its correspond-

ing target. We notice that our approach is not time-

consumer. The total time of computation of all these

energies is 0.25 seconds. We have used Matlab to im-

plement our method.

a b

c d

Figure 7: Ant sequence. Frames {10, 25, 35,45}. (a-b) Ac-

quisitions at t −2 and t −1; (c) Available observation at t;

(d) Frame at t + 1.

4 CONCLUSION

This work proposes a new method for data association

based on an energy minimization. The developed ap-

proach can handle complex motions and highly non-

linear systems, and deals with the lack of prior knowl-

edge. Its effectiveness returns to the fact it requires

few parameters. The geometric illustration of energy

components allows to measure the accuracy between

two dynamic models and to deﬁne their degree of

similarity. As a perspective, we suggest to integrate

the energy minimization approach within the classi-

cal particle ﬁlter to build a new framework for multi-

ple tracking objects. Moreover, since we consider er-

ratic motions that cannot be learned from training se-

quences, we suggest to use an adaptive and automated

way to set the parameters of the dynamic model of

the ﬁlter. The purpose of developing this framework

is to track targets under the restriction of the missing

of prior information and especially when similar tar-

gets are evolving in the scene. This phase is currently

under development.

REFERENCES

Abed, A. E., Dubuisson, S., and B

eziat, D. (2006). Com-

parison of statistical and shape-based approaches for

non-rigid motion tracking with missing data using a

particle ﬁlter. In Advanced Concepts for Intelligent

Vision Systems.

Blake, A. and Isard, M. (1998). Active contours. In

Springer-Verlag.

Fortmann, T., Bar-Shalom, Y., and Scheffe, M. (1983).

Sonar tracking of multiple targets using joint proba-

bilistic data association. In IEEE Journ. Oceanic En-

gineering.

North, B., Blake, A., Isard, M., and Rittscher, J. (2000).

Learning and classiﬁcation of complex dynamics. In

IEEE Transactions on Pattern Analysis and Machine

Intelligence.

Rasmussen, C. and Hager, G. (2001). Probabilistic data

association methods for tracking complex visual ob-

jects. In IEEE Transactions on Pattern Analysis and

Machine Intelligence.

Rong, L. and Bar-Shalom, Y. (1996). Tracking in clut-

ter with nearest neighbor ﬁlter: analysis and perfor-

mance. In IEEE transactions on aerospace and elec-

tronic systems.

Vermaak, J., Godsill, S., and P

erez, P. (2005). Monte carlo

ﬁltering for multi-target tracking and data association.

In IEEE Transactions on Aerospace and Electronic

Systems.

Table 6: First column and ﬁrst row contain ant’s numbers

and measurement’s numbers. The energies magnitude are

multiplied by 100.

)

k×100

1 2 3 4 5 6

1 6.512 47.239 25.761 43.975 48.705 46.618

2 22.545 5.762 21.381 6.498 2.510 12.014

3 15.105 24.891 4.043 17.747 23.748 19.693

4 21.447 1.728 21.604 9.403 5.444 10.209

5 18.317 6.094 17.943 12.191 9.276 5.953

6 16.074 13.549 9.268 10.923 10.318 5.513

)

k×100

1 2 3 4 5 6

1 1.487 1.848 1.424 1.081 11.276 1.091

2 3.096 1.234 3.091 9.610 54.460 1.583

3 14.168 0.234 0.343 0.160 1.256 0.107

4 6.564 2.211 2.669 0.307 24.120 4.400

5 74.366 85.842 92.240 96.185 6.993 92.438

6 0.320 0.255 0.233 1.032 1.895 0.381

)

k×100

1 2 3 4 5 6

1 0.037 45.813 0.792 14.091 48.144 43.240

2 6.801 0.014 24.593 0.225 14.570 13.635

3 22.205 8.488 1.783 5.637 4.657 24.499

4 38.757 14.837 27.829 0.708 17.822 12.073

5 8.457 10.537 12.624 3.231 4.048 6.203

6 23.743 20.101 32.380 76.319 10.759 0.350

)

k×100

1 2 3 4 5 6

1 3.856 38.008 14.903 26.668 40.071 36.715

2 13.713 3.402 18.899 6.699 32.580 10.532

3 17.530 15.184 2.559 10.751 13.991 18.148

4 25.853 8.718 20.399 5.447 17.598 9.475

5 44.487 50.057 54.741 56.008 7.103 53.600

6 16.555 13.996 19.446 44.516 8.676 3.197