PARAMETERIZED KERNELS FOR SUPPORT VECTOR MACHINE
CLASSIFICATION
Fernando De la Torre and Oriol Vinyals
Robotics Institute, Carnegie Mellon University, Pittsburgh, USA
Keywords:
Visual Learning, Kernel methods, Support Vector Machines, Metric learning.
Abstract:
Kernel machines (e.g. SVM, KLDA) have shown state-of-the-art performance in several visual classification
tasks. The classification performance of kernel machines greatly depends on the choice of kernels and its
parameters. In this paper, we propose a method to search over the space of parameterized kernels using
a gradient-based method. Our method effectively learns a non-linear representation of the data useful for
classification and simultaneously performs dimensionality reduction. In addition, we introduce a new matrix
formulation that simplifies and unifies previous approaches. The effectiveness and robustness of the proposed
algorithm is demonstrated in both synthetic and real examples of pedestrian and mouth detection in images.
1 INTRODUCTION
Kernel methods (Schlkopf and Smola, 2002; Shawe-
Taylor and Cristianini, 2004) are increasingly used for
data clustering, modeling and classification problems
because of their state-of-the-art performance, simplic-
ity, and lack of local minima problems. Kernel ma-
chines such as SVM, KPCA, or KLDA project data
into (usually) high dimensional feature spaces, where
linear decision surfaces correspond to non-linear de-
cision surfaces in the original input space. The per-
formance of any kernel machine mostly depends on
the type of kernel and its parameters. The kernel
explicitly defines a similarity measure between two
samples and implicitly represents the mapping of the
input space to the feature space. In general, differ-
ent problems require different feature spaces, and a
domain-specific kernel is a useful feature for an algo-
rithm to have. In this paper, we propose a method to
learn a non-linear mapping of the data (i.e. a kernel)
useful to improve classification in kernel machines.
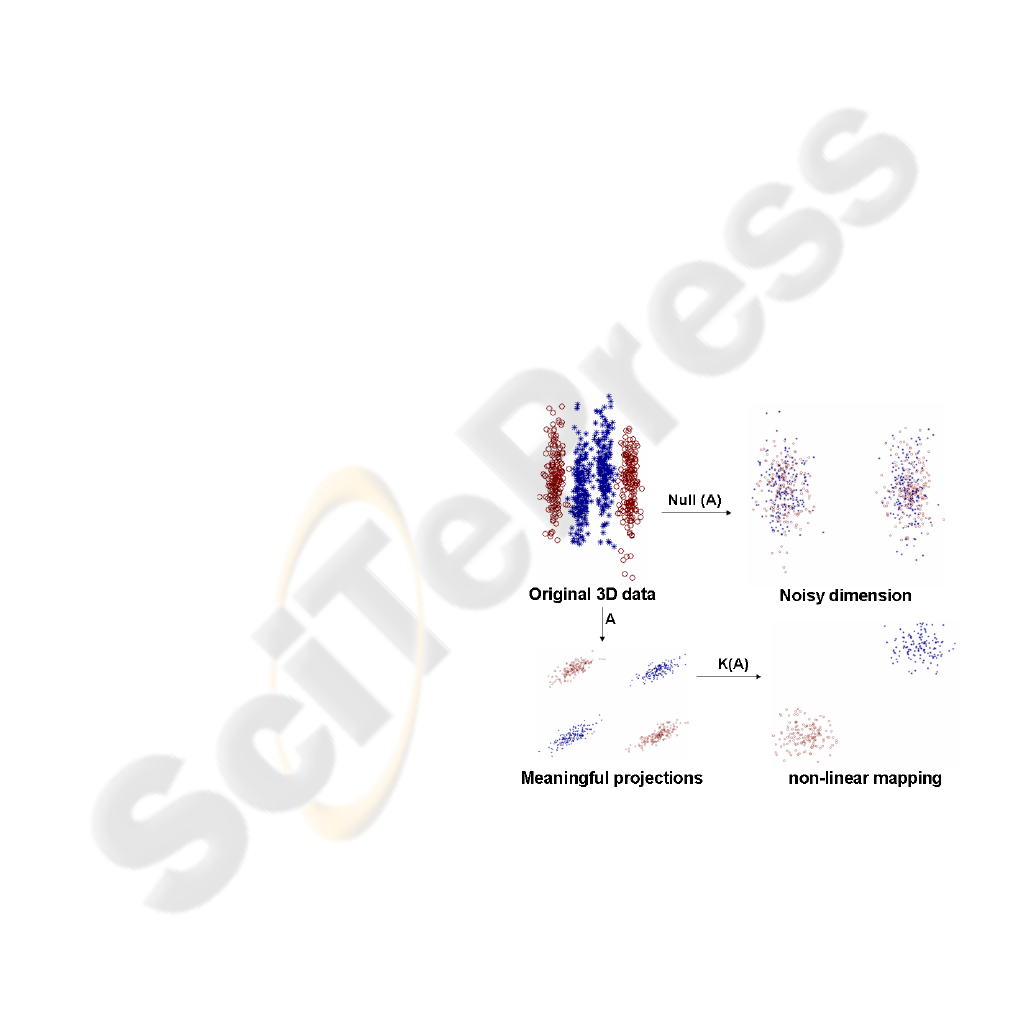
Fig. 1 shows the main point of this paper. We
have synthetically generated 2 multimodal three di-
mensional Gaussian classes. Two of the dimensions
are relevant for classification and the other dimension
is high-variance random Gaussian noise. Our algo-
rithm finds a low dimensional non-linear embedding
Figure 1: Learning a non-linear mapping optimal for classi-
fication. Top left: original data. Top right: useless features
for classification. Bottom left: meaningful projections that
preserve discriminability. Bottom right: final non-linear
learned mapping.
of the data where the data is linearly separable. In
this particular example, our algorithm automatically
finds that the best mapping is a quadratic one, while
discarding the undesirable dimension not relevant for
116
De la Torre F. and Vinyals O. (2007).
PARAMETERIZED KERNELS FOR SUPPORT VECTOR MACHINE CLASSIFICATION.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 116-121
Copyright
c
SciTePress

classification. Observe that with a Gaussian kernel
we could achieve similar classification performance
in this particular problem (assuming some tuning of
the parameters is done); however, the exponential ker-
nel hides the simplicity of the solution found by our
algorithm (a quadratic mapping).
2 PREVIOUS WORK
Since the introduction of kernel machines in the 90’s,
there has been growing literature on metric and kernel
learning. It is beyond the scope of this paper to review
all previous work along these lines, but a good re-
view on metric learning can be found in (Yang, 2006),
and for kernel selection methods see (Schlkopf and
Smola, 2002; Shawe-Taylor and Cristianini, 2004).
A common approach to learn a kernel matrix uses
semi-definite programming (SDP) (Lanckriet et al.,
2004; Cristianini et al., 2001) to maximize some sort
of alignment with respect to an ideal kernel. A ma-
jor limitation of SDP is its computational complexity,
since it scales O(n
6
), where n is the number of sam-
ples (Boyd and Vandenberghe, 2004). This limita-
tion has restricted its application to small scale prob-
lems. Recently, (Kim et al., 2006) posed the ker-
nel selection for kernel linear discriminant analysis
as a convex optimization problem. To optimize over
a positive combination of known kernels, they use
interior point methods with a computational cost of
O(d
3
+ n
3
), where d is the dimension of the samples.
Along these lines, (Weinberger et al., 2006) learns a
Mahalanobis distance metric in the kNN classification
setting by SDP. The learned distance metric enforces
the k-nearest neighbors to belong to the same class,
while examples from different classes are separated
by a large margin.
In the literature of metric learning, Goldberger et
al. (Goldberger et al., 2004) have proposed Neighbor
component analysis that computes the Mahalanobis
distance that minimizes an approximation of the clas-
sification error. Similarly, (Shental et al., 2002) opti-
mizes the linear discriminant analysis (LDA) criteria
in a semi-supervised manner to learn the metric.
In previous work, typically, a parameterized fam-
ily of linear or non-linear kernels, (e.g. Gaussian,
polynomial ) are chosen and the kernel parameters are
tuned with some sort of cross-validation. In this pa-
per, we consider the more generic problem of finding
a functional mapping of the data.
3 PARAMETERIZING THE
KERNEL
Many visual classification tasks (e.g. object recogni-
tion) are highly complex and non-linear kernels are
needed to model changes such as illumination, view-
point or internal object variability. Learning a non-
linear kernel is a relatively difficult problem; for in-
stance, proving that a function is a kernel is a chal-
lenging mathematical task. A given function is a
kernel if and only if the value it produces for two
vectors corresponds to a dot product in some feature
Hilbert space. This is the well known Mercer’s the-
orem: ”Every positive definite, symmetric function
is a kernel. For every kernel K, there is a function
ϕ(x) : k(d
1
,d
2
) = hϕ(d
1
),ϕ(d
2
)i.”, where hi denotes
dot product. To avoid the problem of proving that a
similarity function is a kernel, it is common to param-
eterize the Kernel as a positive combination of exist-
ing Kernels (e.g. Gaussian, polynomial, ...).
In this paper, we propose to learn a kernel as a pos-
itive combination of normalized kernels as follows:
T = D
T
AD
ˆ
T = dm(T)
−
1
2
Tdm(T)
−
1
2
T
t
= D
T
A
t
D
ˆ
T
t
= dm(T
t
)
−
1
2
T
t
dm(T
t
)
−
1
2
K
1
(A,α) =
∑
p
t=0
α
t
ˆ
T
t
K
2
(A
1
,··· ,A
p
,α) =
∑
p
t=0
α
t
ˆ
T
t
t
(1)
where α
t
≥ 0 ∀t, the columns of D ∈ ℜ
d×n
(see nota-
tion
1
) contain the original data points, d denotes the
dimension of the data, n the number of samples and
p the degree of the polynomial. Each element i j of
the matrix T, t
i j
= d
T
i
Ad
j
contains the dot weighted
product between the sample i and j. Each element i j
of the matrix
ˆ
T represents the cosine of the angle be-
tween the samples i and j (i.e.
ˆ
t
i j
=
d
T
i
Ad
j
q
d
T
j
Ad
j
d
T
i
Ad
i
).
ˆ
T
k
exponentiates each of the entries in T. K
1
is a
positive combination of
ˆ
T
k
, and if A is positive def-
inite, K
1
will be a valid kernel because of the closure
1
Bold capital letters denote a matrix D, bold lower-case
letters a column vector d. d
j
represents the j column of the
matrix D. d
i j
denotes the scalar in the row i and column
j of the matrix D and the scalar i-th element of a column
vector d
j
. All non-bold letters will represent variables of
scalar nature. d iag is an operator that transforms a vector
to a diagonal matrix or takes the diagonal of the matrix into
a vector. dm(A) is a matrix that contains just the diagonal
elements of A. ◦ denotes the Hadamard or point-wise prod-
uct. 1
k
∈ ℜ
k×1
is a vector of ones. I
k
∈ ℜ
k×k
is the iden-
tity matrix. tr(A) =
∑
i
a
ii
is the trace of the matrix A and
|A| denotes the determinant. ||A||
F
= tr(A
T
A) designates
the Frobenious norm of a matrix. A
k
denotes point-wise
power, i.e. a
k
i j
∀i, j.
PARAMETERIZED KERNELS FOR SUPPORT VECTOR MACHINE CLASSIFICATION
117

properties of kernels (Shawe-Taylor and Cristianini,
2004). The rank of each of the matrices
ˆ
T and
ˆ
T
t
is
min{d,n}, but K
1
might be full rank. The same in-
terpretation holds for K
2
with the difference that for
each kernel
ˆ
T
t
there is a different metric matrix A
t
,
that is, each kernel might have a different subspace to
project the data onto. The matrix A
t
models correla-
tions between variables.
The kernel expansion suggested in eq. 1 is, in
spirit, similar to the Taylor series expansion of a mul-
tivariate function. In fact, K
1
and K
2
can represent
directly the polynomial kernel and are closely related
to the exponential one. Consider a set of normalized
samples (i.e.
ˆ
d
i
= d
i
/||d
i
||
2
), the Taylor series expan-
sion of two elements of the exponential kernel will be
k
i j
= e
||
ˆ
d
i
−
ˆ
d
j
||
2
2
σ
2
=
∑
∞
i=0
(2)
i
σ
2i
i!
(1 −
ˆ
d
T
i
ˆ
d
j
)
i
, which has an
identical form of the expansion proposed in eq. 1 if
A
t
= I
d
∀t. Observe that our kernel expansion is more
flexible and it will learn a mapping useful for classi-
fication from training data. However, K
1
and K
2
are
not translational invariant kernels.
3.1 Dealing with High Dimensional
Data
For high dimensional data (e.g. images) A ∈ℜ
d×d
is
a big matrix that captures the correlation relation be-
tween the features. In our context, working with these
very high dimensional matrices presents two prob-
lems: computational tractability (storage, efficiency
and rank deficiency) and generalization.
In order to be able to generalize better and to not
suffer from storage/computational limitations, we fol-
low recent work (de la Torre and Kanade, 2005) and
factorize the matrix A as a low dimensional subspace
plus a noisy term (scaled identity matrix). That is,
we approximate each matrix A
t
as A
t
≈ B
t
B
T
t
+ λ
t
I
d
where λ
t
≥ 0 ∈ ℜ and B
t
∈ ℜ
d×k
. It is worthwhile to
point out two important aspects of the previous fac-
torizations. Factorizing the covariance as the sum of
outer products and a diagonal matrix is an efficient
(in space and time) manner to reduce the dimension-
ality of the data. Firstly, observe that to compute
Ad
i
≈B(B
T
d
i
)+λd
i
storing/computing the full d ×d
covariance is not required. Secondly, the original ma-
trix A has d(d + 1)/2 free parameters, and after the
factorization the number of parameters is reduced to
k(2d −k + 1)/2 (assuming orthogonality of B), and
hence is not so prone to over-fitting.
4 LEARNING FROM AN IDEAL
KERNEL
In the previous section, we have proposed a possi-
ble expansion of a parameterized kernel. Ideally, we
would like to directly optimize the kernel parameters
to minimize the Bayes classification error; however,
this is usually a hard task because the underlying dis-
tribution of the data is unknown and usually some sort
of bounds are optimized instead. In this section, we
explore the use of a ideal reference kernel to learn the
kernel parameters.
In the ideal case, we would like to estimate the
parameters of the kernel (A,α) to produce a block di-
agonal matrix (assuming samples are ordered). That
is, in all the samples that belong to the same class the
kernel function should output a similarity of 1 and 0
otherwise. This ideal matrix can be computed with
the matrix G as F = GG
T
. A reasonable measure of
distance between the ideal kernel and the parameter-
ized one is given by:
E
1
(A,α) = ||F −K(A,α)||
F
∝
tr(K(A,α)K(A,α)
T
) −2tr(K(A,α)F) (2)
This measure of distance between kernels is
closely related to the one proposed by (Cristianini
et al., 2001). Cristianini et al. propose to mini-
mize the alignment between kernels with: E
2
(A,α) =
tr(K(A,α)F)
√
tr(K(A,α)K(A,α))
. Minimization of E
1
is more
convenient to optimize and very similar (but not
equivalent) to maximization of E
2
. Recall that if
we take the log E
2
and change the sign, E
2
∝
0.5log(tr(K(A,α)
2
)) −logtr (K(A, α)F).
One drawback of eq. 2 is that it enforces the same
similarity measure (i.e. 1) for two samples of the
same class that are near or far away in the input space.
This behavior can produce over-fitting and it can re-
move important information regarding class discrim-
inability. Moreover, we can have an unbalanced prob-
lem where a particular class has more samples than
another one, and we would like a mechanism to com-
pensate for that. Furthermore, any real data set con-
tains a number of outliers that can bias the solution.
To account for these situations, we introduce a new
distance matrix W ∈ ℜ
n×n
that will weight individ-
ually each pair-wise points. For instance, to account
for outliers we will weight all the rows and columns
of the outlying data as 0, or to compensate for the fact
that two samples have large dissimilarity in the input
space, we enforce a small link between these samples
e.g w
i j
= e
−
||d
i
−d
j
||
2
2
β
2
∀i 6= j. To incorporate W in the
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
118

formulation, we modify eq. 2 as:
E
3
(A,α) = ||W ◦(F −K(A,α))||
F
∝
tr((W ◦K(A,α))(K(A,α) ◦W)
T
)
−2tr((W ◦K(A,α))(W ◦F)) (3)
5 LEARNING THE KERNEL
In this section, we derive several optimization strate-
gies to learn a parameterized kernel.
5.1 Optimizing w.r.t A and α
In the interest of space, we derive the optimization
rules for the most generic error function. In particular,
we show how to optimize:
E
4
(A
1
,··· ,A
p
,α) = ||W ◦(F −K
2
)||
F
(4)
w.r.t. A
1
,··· ,A
p
,α, since optimizing K
1
is very sim-
ilar. To optimize eq. 4, we use an alternating strat-
egy of fixing A
t
parameters and optimize w.r.t. α and
vice versa. This will monotonically decrease the error
of E
4
. If α is known, optimizing over A
t
matrix can
be formulated as a semi-definite programming prob-
lem (SDP); however, the computational complexity is
large. Instead, we use a gradient descent approach to
incrementally optimize for A
t
. The gradient updates
are given by:
A
n+1
t
= A
n
t
−η
∂E
4
(K
2
)
∂A
t
(5)
∂E
4
∂A
t
= 2α
t
tD(M
2
−M
3
)D
T
∀t
M
1
= (K
1
−F) ◦
ˆ
T
(t−1)
t
◦W
2
M
2
= dm(T
t
)
−
1
2
M
1
dm(T
t
)
−
1
2
M
3
= dm(T
t
)
−
3
2
diag
(dm(T
t
)
−
1
2
M
1
◦T
t
)1
n
The major problem with the update of eq. 5 is to
determine the optimal η. In our case, η is determined
with a line search strategy (Fletcher, 1987). Similarly,
for high dimensional data the gradient w.r.t B
t
is:
B
n+1
t
= B
n
t
−η
∂E
4
(K
2
)
∂B
t
(6)
∂E
4
∂B
t
= 2α
t
tD(M
2
−M
3
)D
T
B
t
∀t
At this point, it is worthwhile to mention that the com-
plexity of the updates is O(d + n
2
), far less expensive
than SDP approaches. λ
t
is optimized using the fmin-
con function from Matlab
c
to ensure positiveness.
Once all A
t
∀t have been updated, α values can be
optimized using quadratic programming. After rear-
ranging, eq. 4 can be expressed as:
E
5
(α) ∝ α
T
Zα −2p
T
α α ≥0 (7)
where z
i j
=
∑
lk
w
2
lk
k
i
lk
k
j
lk
and p
i
=
∑
lk
w
2
lk
f
lk
k
i
lk
. Re-
call that k
i j
corresponds to the i j element of K
2
. We
use the quadprog function from Matlab
c
to opti-
mize w.r.t.α to ensure positiveness.
5.2 Initialization and Other Issues
Minimizing eq. 4 w.r.t to α, A
1
,··· ,A
p
is a non-
convex optimization problem prone to many local
minima. Without a good initial estimation, the pre-
vious optimization scheme easily converges to a local
minima. To get a reasonable estimation, we initial-
ize each of the parameters A
1
,··· ,A
p
with the LDA
solution and the means of the clusters resulting from
k-means clustering. The α values are initialized with
the same uniform value. Moreover, we start from sev-
eral random initial points and select the solution with
minimum error after convergence.
To avoid over-fitting problems and for computa-
tional convenience, we train the algorithm stochasti-
cally. That is, we randomly select subsets of training
data, run few iterations of the gradient descent algo-
rithm, select other random subset of data and proceed
this way until convergence.
6 EXPERIMENTS
In this section, we report comparative results of our
algorithm with standard SVM approaches in image
classification problems. In all the experiments we
have used the C-SVM implementation (Chang and
Lin, 2001).
6.1 Synthetic Data
Consider fig. 1, where 200 samples have been gener-
ated from four 3D Gaussians (50 each) from 2 differ-
ent classes (”exclusive or” (XOR) problem). For each
of the Gaussians, the z coordinate is random noise of
high variance.
In this case, we learn a common matrix A ∈ ℜ
3×3
and the α values. After convergence, the rank of the
matrix A is 3 with eigenvalues l
1
= 1.9860 l
2
=
0.6843 l
3
= 0.0009, the small eigenvalue corre-
sponds to the eigenvector aligned with the z direc-
tion, where the non-discriminative information lies.
That is, the null space of A contains the random non-
discriminative directions. Even more interesting is the
interpretation of the α parameters. All the α param-
eters are close to 0 except for the powers of 2. This
is because, for samples within the same cluster, the
cosine of the angle will be approximately 1; between
the samples of a different cluster but of the same class
PARAMETERIZED KERNELS FOR SUPPORT VECTOR MACHINE CLASSIFICATION
119


Table 1: Average classification results for different kernels.
Features Linear Exponential Ours
Graylevel 73.9 76.4 84.2
Multiband 72.4 79.1 84.9
Figure 5: a) Some training examples of the IBM Database.
b) First row the same images with our learned kernel (3/3).
Second row some test images using the RBF SVM (1/3).
Figure 6: Roc curves of RBF versus our algorithm.
possible locations of the image. Evaluating the kernel
at each location (x, y) can be computationally expen-
sive. For a particular position (x,y) computing the
projection B
T
t
d
i
is equivalent to correlating the im-
age with each basis of the subspace B
t
, and stacking
all the values for each pixel. For large regions, this
correlation is performed efficiently in the frequency
domain using the Fast Fourier Transform (FFT) (i.e.
C
1
= b
T
1
I = IFFT (FFT (b
1
) ◦FFT (I))). This fast
search is another advantage of our formulation. Fig. 6
shows the average ROC curve over 14 images for our
kernel and RBF kernel. The parameters of the RBF
kernel (i.e. e
−||x
i
−x
j
||
2
2
2σ
2
, σ and the C in the C-SVM
are tuned with a cross validation procedure. Similarly
the C parameter in the C-SVM is tuned with cross-
validation. Fig. 5.b shows some examples of the
detection performance of the RBF-SVM versus our
learned kernel. In the first row, our learned kernel de-
tects two out of three mouths, whereas in the second
row RBF only detects one.
ACKNOWLEDGEMENTS
The work was partially supported by grants from
the National Institute of Justice (award 2005-
IJ-CX-K067) and Defense Advanced Research
Projects Agency (DARPA) under Contract No.
NBCHD030010. Thanks to Minh Hoai Ngyen for
helpful discussions and comments.
REFERENCES
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press.
Chang, C.-C. and Lin, C.-J. (2001). LIBSVM: a library
for support vector machines. Software available at
http://www.csie.ntu.edu.tw/ cjlin/libsvm.
Cootes, T. F. and Taylor, C. J. (2001). Statistical
models of appearance for computer vision. In
http://www.isbe.man.ac.uk/bim/refs.html.
Cristianini, N., Taylor, J. S., and Elisseeff, A. (2001). On
kernel-target alignment. In NIPS.
de la Torre, F. and Kanade, T. (2005). Multimodal oriented
discriminant analysis. In ICML.
Fletcher, R. (1987). Practical methods of optimization. John
Wiley and Sons.
Goldberger, J., Roweis, S., Hinton, G., and Salakhutdinov,
R. (2004). Neighbourhood component analysis. In
NIPS, pages 513–520.
Kim, S.-J., Magnani, A., and Boyd, S. (2006). Optimal
kernel selection in kernel fisher discriminant analysis.
In ICML, pages 465–472.
Lanckriet, G., Cristianini, N., Bartlett, P., Ghaoui, E., and
Jordan, M. (2004). Learning the kernel matrix with
semidefinite programming. (5):27–72.
Munder, S. and Gavrilla, D. (2006). An experimental study
on pedestrian classifcation.
Neti, C., Potamianos, G., Luettin, J., Matthews, I., Glotin,
H., Vergyri, D., Sison, J., Mashari, A., and Zhou,
J. (2000). Audio-visual speech recognition. Tech-
nical Report WS00AVSR, Johns Hopkins University,
CLSP.
Schlkopf, B. and Smola, A. (2002). Learning with Kernels:
Support Vector Machines, Regularization, Optimiza-
tion, and Beyond. MIT Press.
Shawe-Taylor, J. and Cristianini, N. (2004). Kernel Meth-
ods for Pattern Analysis. Cambridge university press.
Shental, N., Hertz, T., Weinshall, D., and Pavel, M. (2002).
Adjustment learning and relevant component analysis.
In European Conferenceon Computer Vision, pages
776–790.
Weinberger, K., Blitzer, J., and Saul, L. (2006). Neighbour-
hood component analysis. In NIPS.
Yang, L. (2006). Distance metric leraning: A comprehen-
sive survey.
PARAMETERIZED KERNELS FOR SUPPORT VECTOR MACHINE CLASSIFICATION
121
