3D VOLUME WATERMARKING USING 3D KRAWTCHOUK

MOMENTS

Athanasios Mademlis

Information Processing Laboratory, Aristotle University of Thessaloniki, 54006, Thessaloniki, Greeece

Petros Daras, Dimitrios Tzovaras

Informatics and Telematics Institute, Centre For Research and Technology Hellas, 57001, PO Box 60361, Thessaloniki, Greece

Michael G. Strintzis

Information Processing Laboratory, Aristotle University of Thessaloniki, 54006, Thessaloniki, Greeece and

Informatics and Telematics Institute, Centre For Research and Technology Hellas, 57001, PO Box 60361, Thessaloniki, Greece

Keywords:

Watermarking, Data Hiding, 3D volume, 3D Krawtchouk moments.

Abstract:

In this paper a novel blind watermarking method of 3D volumes based on the Weighted 3D Krawtchouk

Moments is proposed. The watermark is created by a pseudo-random number generator and is embedded on

low order Weighted 3D Krawtchouk Moments. The watermark detection is blind, requiring only the user’s

key. The watermark bit sequence is created using the key and its cross correlation with the Weighted 3D

Krawtchouk Moments of the possible watermarked volume. The proposed method is imperceivable to the

user, robust to geometric transformations (translation, rotation) and to cropping attacks.

1 INTRODUCTION

In the recent past, with the rapid development of 3D

computing application, huge amount of multimedia

data have become publicly available (photographs,

videos, paintings, music etc). Moreover, the rapid

growth of Internet has increased the number of chan-

nels for digital data distribution. In this environment,

the need for protection of copyrighted digital data is

obvious. The most classic method to achieve the lat-

ter is the watermarking. Extra information (the water-

mark), is hidden with an appropriate algorithm in the

digital data in a way that is imperceptible from the

user, but it can be perceived by an appropriate detec-

tion algorithm.

A watermarking algorithm has to fulﬁl the follow-

ing criteria:

• Robustness against attacks: The watermark has to

be detectable if the digital data are intentionally or

unintentionally modiﬁed.

• Invisibility: The user must not be able to perceive

that the digital data are watermarked.

Concerning color and grayscale 3D volumes, only

few methods have been presented so far. The major-

ity of the methods hide the watermark in appropri-

ate coefﬁcients of an invertible transformation (e.g.

DCT (Wu et al., 2001), Fourier (Solachidis and Pitas,

2005), wavelet (Wu et al., 2001)). The watermark

affects the appropriate parameters in order to ensure

both imperceptibility and robustness against various

attacks. For example, in the secure Fourier-based

watermarking technique presented in (Solachidis and

Pitas, 2005), the watermark is embedded in the mid-

dle frequency coefﬁcients, because the low frequency

coefﬁcients can alter the initial volume in a way that is

visible to the user and the high frequency coefﬁcients

can be easily ﬁltered. There are also other approaches,

(e.g. (Tefas et al., 2002), (Louizis et al., 2002)) in

which the 3D volume is modiﬁed in the spatial do-

main, using appropriate embedding functions.

In this paper, a novel blind 3D volume watermark-

ing technique which utilizes the 3D Krawtchouk mo-

ments presented in (Mademlis et al., 2006) is pro-

posed, in order to watermark 3D volumes. The

projection of any 3D volume to the space of

Weighted 3D Krawtchouk moments, which is fully

reversible. Moreover, the Weighted 3D Krawtchouk

Moments are deﬁned in the discrete ﬁeld, thus no

discretization error is inserted during the Weighted

3D Krawtchouk moments analysis. Also, the pro-

posed 3D Krawtchouk watermarking method is robust

280

Mademlis A., Daras P., Tzovaras D. and G. Strintzis M. (2007).

3D VOLUME WATERMARKING USING 3D KRAWTCHOUK MOMENTS.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 280-283

 SciTePress

against the geometric transformations of rotation and

translation and against cropping attacks.

The rest of the paper is organized as follows.

In Section 2 a brief overview of the Weighted 3D

Krawtchouk Moments is given. The watermark em-

bedding approach is presented in Section 3, while the

watermark detection algorithm is analyzed in Section

4. In Section 5 the experimental results are presented

and ﬁnally the conclusions are drawn in Section 6.

2 3D KRAWTCHOUK MOMENTS

3D Krawtchouk Moments have been introduced in

(Mademlis et al., 2006) and exploited for 3D object

search and retrieval applications. In this paper, this

theory is utilized for watermarking purposes. For the

shake of completeness, the theory of 3D Krawtchouk

Moments is brieﬂy described in the sequel.

The n-order Krawtchouk classical polynomials

(Koekoek and Swarttouw, 1998) are deﬁned in terms

of the hyper-geometric function as:

(x; p,N) =

∑

k=0

k,n,p

(−n,−x;−N;

) (1)

where x,n = 0,1,2...N,N > 0, p ∈ (0,1) and the

function

is the hypergeometric function.

The set of Krawtchouk polynomials S = {

(x; p,N),n = 0...N } has N +1 elements and forms

a complete set of discrete basis functions with weight

function:

w(x; p,N) =





(1− p)

N−x

(2)

Krawtchouk Polynomials are orthogonal:

∑

x=0

w(x; p,N)K

(x; p,N)K

(x; p,N) = (3)

= ρ(n; p,N)δ

(4)

where n,m = 1, 2,3...N,

ρ(n; p, N) = (−1)



1− p



(−N)

(5)

and δ

is the Kronecker delta function.

Let f(x,y,z) be a 3D function deﬁned in a dis-

crete ﬁeld A = {(x,y,z) : x,y, z ∈ IN , x = [0. ..N − 1],

y = [0... M − 1], z = [0... L− 1]}. The Weighted 3D

Krawtchouk moments of order (n+m+l) of f, are de-

ﬁned as (Mademlis et al., 2006):

nml

N−1

∑

x=0

M−1

∑

y=0

L−1

∑

z=0

(x; p

,N − 1) ×

(y; p

,M − 1)

(z; p

,L− 1) ×

× f(x,y, z) (6)

where

(x; p,N) is the family of weighted

Krawtchouk polynomials deﬁned as:

(x; p

,N − 1) = K

(x; p,N)

w(x; p,N)

ρ(n; p, N)

(7)

Due to the orthonormality property of the

Weighted 3D Krawtchouk Moments:

f(x,y, z) =

N−1

∑

x=0

M−1

∑

y=0

L−1

∑

z=0

(x; p

,N − 1) ×

(y; p

,M − 1)

(z; p

,L− 1) ×

nml

(8)

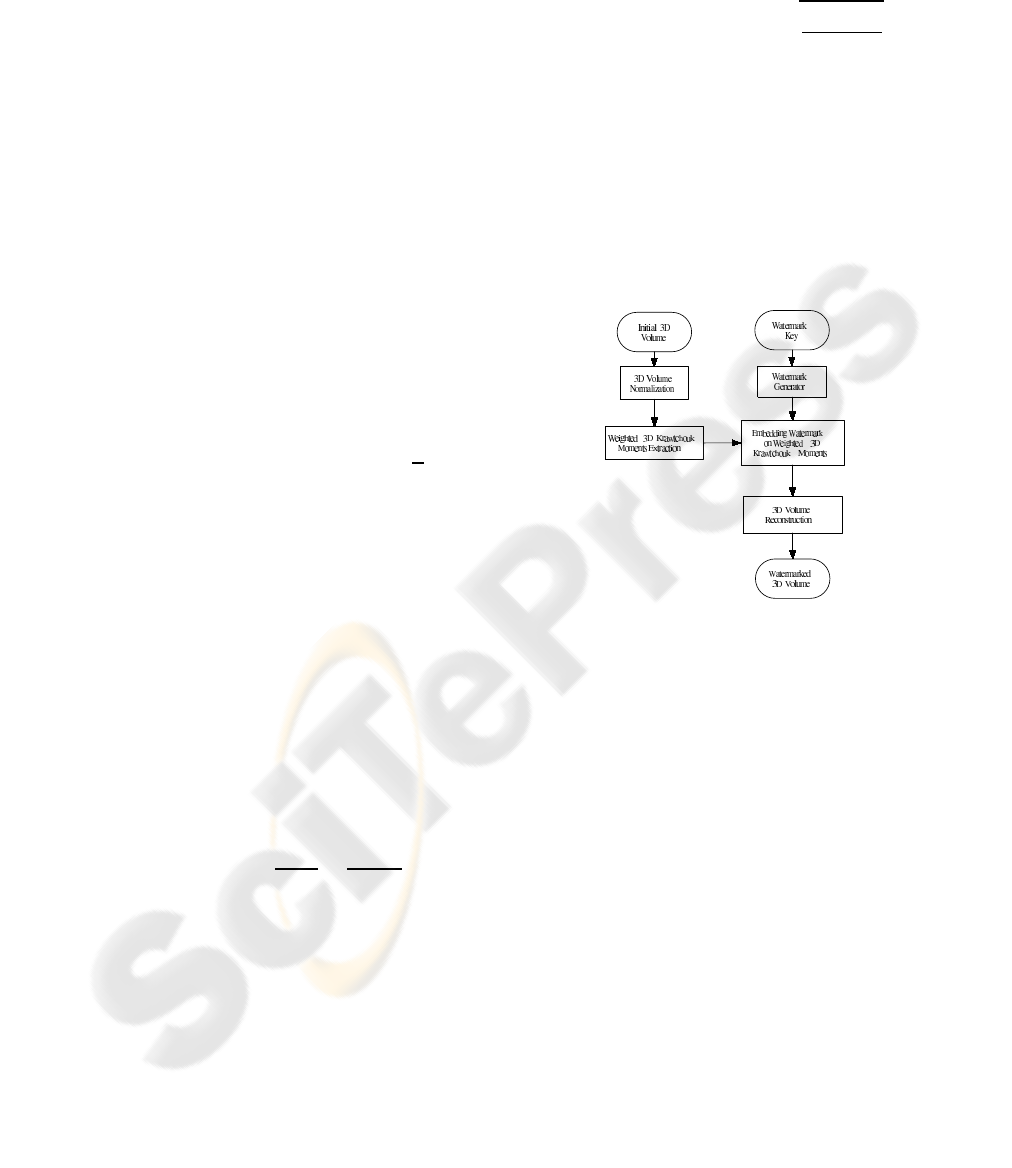
Figure 1: The watermark embedding procedure.

3 WATERMARK EMBEDDING

The watermark generation procedure aims at gener-

ating a two-valued watermark series w

nml

∈ {−1,1},

n = 0. ..N

− 1, m = 0.. .M

− 1, l = 0.. . L

− 1,

where N

∗ M

∗ L

is the watermark length, and N

≤

N, M

≤ M, L

≤ L. The watermark bits are produced

by a method that relies on a seed, which completely

deﬁnes it. In this paper a pseudo-random number gen-

erator is utilized. Alternatively, a chaotic sequence

could be used.

Let O be the initial 3D volume, represented by

the volumetric function f

(x,y, z). Firstly, O is nor-

malized for rotation and translation and the computed

normalization parameters are stored for the recon-

struction process. For translation normalization, the

3D volume is translated so as the mass center of the

object is placed on [N/2,M/2,L/2]. For achieving

rotation normalization, the classical Principal Com-

ponent Analysis (PCA) is followed. Finally, the

Weighted 3D Krawtchouk moments are extracted ac-

cording to (6).

The watermark is embedded in the low order

Weighted 3D Krawtchouk moments as follows:

′

nml

= (1 + αw

nml

) ∗

nml

(9)

where α is the embedding strength of the water-

mark,

nml

are the Weighted 3D Krawtchouk Mo-

ments of the initial object and

′

nml

are the Weighted

3D Krawtchouk Moments of the watermarked object.

Finally, the watermarked object is reconstructed

from the Weighted 3D Krawtchouk Moments accord-

ing to (8) and it is translated and oriented to initial po-

sition, according to the computed normalization para-

meters.

The embedding process is depicted in Figure 1.

3D Volume

Normalization

3D Volume

Weighted 3D Krawtchouk

Moments Extraction

Watermark

Key

Watermark

Generator

Cross Correlation

Decison

Figure 2: The watermark detection procedure.

4 WATERMARK DETECTION

Let O

′

be a possibly watermarked 3D volume and

′

(x,y, z) its volumetric function. The volume is nor-

malized with respect to rotation and translation and

the appropriate Weighted 3D Krawtchouk Moments

′

nml

are computed, according to (6).

The watermark detection is blind, thus only the

key of the owner is needed, which is used for the wa-

termark generation W = [w

nml

In order to detect if a volume is watermarked with

the watermark W, the correlation γ between the possi-

bly watermarked coefﬁcients

nml

and the watermark

W can be used to detect the presence of the water-

mark, in a similar manner to the blind approach of

(Solachidis and Pitas, 2005):

γ =

∑

nml

′

nml

(10)

If the volume is watermarked with the same wa-

termark W:

γ =

∑

mnl

nml

+ α

∑

mnl

nml

(11)

If the volume is watermarked with a different wa-

termark W

′

γ =

∑

mnl

nml

+ α

∑

mnl

nml

′

nml

(12)

Then, assuming that the two watermarks W and

′

are two uncorrelated random variables which are

also uncorrelated to the Weighted 3D Krawtchouk

Moments of the initial model

nml

, then:

E{ γ} =







0 if O

′

is not watermarked

0 if O

′

is watermarked with W

′

A if O

′

is watermarked with W

(13)

where A = αN

nml

Thus, using an appropriately selected threshold

T, which can be computed for every object from the

Weighted 3D Krawtchouk coefﬁcient parameters and

the watermark strength, a decision whether the O

′

watermarked with W can be made. The watermark

detection algorithm is schematically depicted in Fig-

ure 2.

5 EXPERIMENTAL RESULTS

The proposed algorithm has been tested for its perfor-

mance using MRI 3D volumes with size 64× 64× 64

and 128 × 128 × 32. Each 3D volume was water-

marked with a thousand different watermarks with a

length of 216 bits. The watermark is embedded on

Weighted 3D Krawtchouk Moments with n = [0... 5],

m = [0... 5] and l = [0.. .5], watermark strength α =

0.1, and p

= p

= 0.5.

• Imperceptibility: In order to measure the imper-

ceptibility of the embedded watermark, the Peak

Signal-to-Noise Ratio was calculated. The for-

mula used is:

PSNR = 10log

∑

xyz

255

∑

xyz

( f

(x,y, z) − f

′

(x,y, z))

(14)

where f

(x,y, z) and f

′

(x,y, z) are the volumetric

functions of the initial and the watermarked object

respectively.

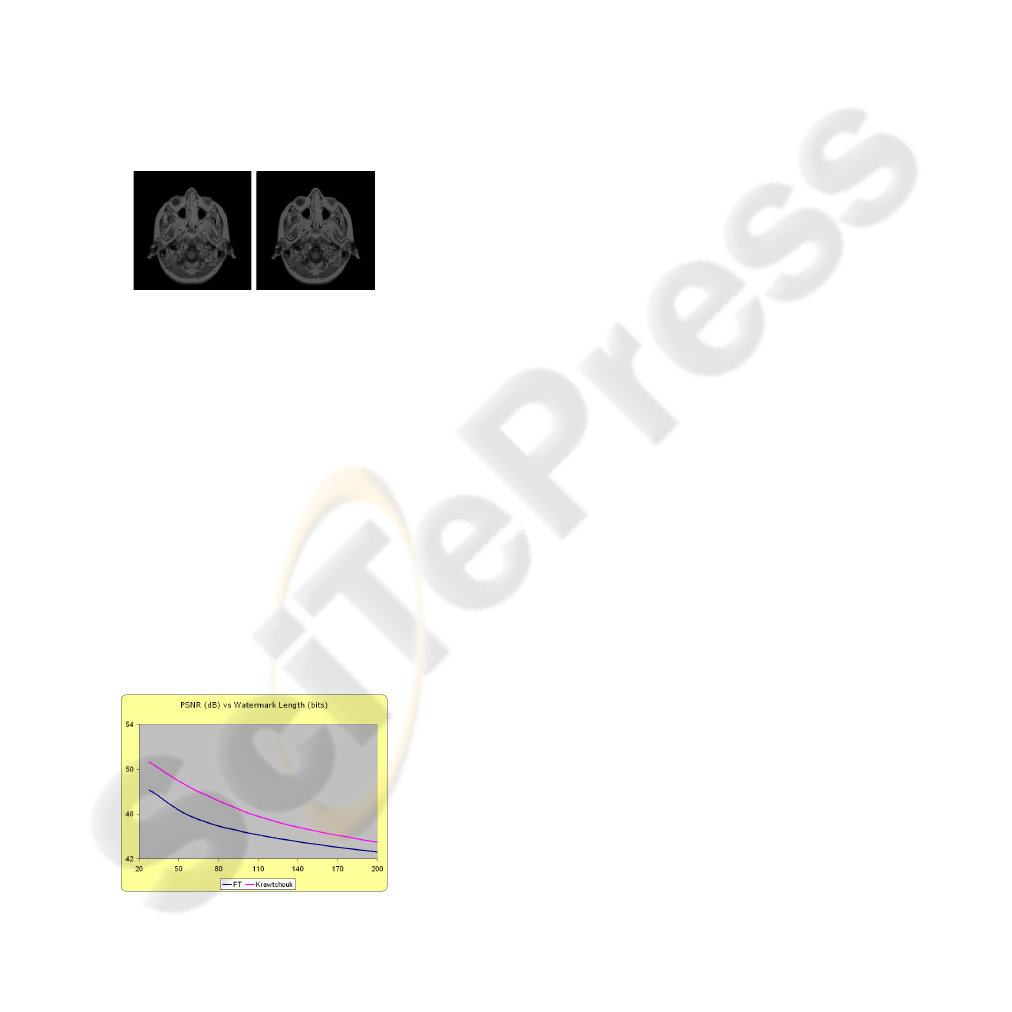
The PSNR value varies between 42 dB and 47 dB,

thus it is expected that the watermark is impercep-

tible to the user. In Figure 3 a slice from the initial

3D volume and the corresponding slice from the

watermarked 3D volume are depicted. Although

the intensity of the voxels has been changed, it is

not perceptible from the user.

• Geometric attacks: The geometric attacks consid-

ered are the rotation and translation. The nor-

malization step which was initially utilized en-

sures invariance under this kind of attacks and the

percentage of correct watermark detections was

100%.

• Cropping: The low level Krawtchouk moments

capture information mainly for a neighborhood

of the 3D volume located around the point

N, p

M, p

L). The higher the order of the poly-

nomials the greater the area. The watermark has

been embedded in the center of the volume, thus,

any cropping attempt that does not affect the wa-

termarked area, does not affect the watermark de-

tection. If the center area of the 3D volume is

removed, the object is not useful.

Figure 3: Slice of the initial 3D volume (top) and the corre-

sponding watermarked slice (bottom).

The proposed algorithm was also tested for its per-

formance for different lengths of the watermark and

was compared to with a similar watermarking ap-

proach based on the Fourier Transform. The same

watermark is embedded both on the Euclidean norm

of middle frequency Fourier coefﬁcients and the low

order Weighted 3D Krawtchouk moments. Figure 4

depicts the performance of the two methods in terms

of PSNR versus watermark length. The experimen-

tal results prove that the proposed Krawtchouk wa-

termarking scheme can achieve more imperceptible

results than the Fourier Transform for the same wa-

termark bit length.

Figure 4: PSNR values for different watermark length.

6 CONCLUSIONS

In this paper, a novel blind method for 3D volume

watermarking was presented. The 3D volume is nor-

malized in terms of rotation and translation in order

to achieve robustness against these geometric trans-

formations. Then, the Weighted 3D Krawtchouk mo-

ments of the 3D volume are extracted and the water-

mark, which is created by a random number generator

having as seed the user’s private key, is embedded on

low order coefﬁcients which capture local informa-

tion around the 3D volume’s mass center of the vol-

ume. For watermark detection, only the owner’s key

is needed, and a decision is made. The experimen-

tal results proved that the method is imperceptible to

the ﬁnal user and robust against geometric transfor-

mations and cropping.

ACKNOWLEDGEMENTS

This work was supported by the VICTORY and

CATER EC IST projects and by the PENED Greek

project.

REFERENCES

Koekoek, R. and Swarttouw, R. F. (1998). The askey-

scheme of hypergeometric orthogonal polynomials

and its q-analogue. In Delft, Netherlands:Technische

Universiteit Delft, Faculty of Technical Mathematics

and Informatics Report 98-17.

tection of 3d images using watermarks of speciﬁc spa-

tial structure. In IEEE International Conference on

Multimedia and Expo. ICME ’02, volume 2, pages

557– 560.

Mademlis, A., Axenopoulos, A., Daras, P., Tzovaras, D.,

and Strintzis, M. G. (2006). 3d content-based search

based on 3d krawtchouk moments. In 3D Data

Processing, Visualization & Transmission (3DPVT

2006), Chapel Hil, North Carolina, USA.

Solachidis, V. and Pitas, I. (2005). Watermarking digital

3d volumes in the discrete fourier transform domain.

In IEEE International Conference on Multimedia and

Expo. ICME 2005.

Tefas, A., Louizis, G., and Pitas, I. (2002). 3d image wa-

termarking robust to geometric distortions. In IEEE

International Conference on Acoustics, Speech, and

Signal Processing, (ICASSP ’02)., volume 4, pages

IV–3465– IV–3468.

Wu, Y., Guan, X., Kankanhalli, M., and Huang, Z. (2001).

Robust invisible watermarking of volume data using

the 3d dct. In Computer Graphics International, Hong

Kong, China.