MODEL-BASED SHAPE FROM SILHOUETTE

A Solution Involving a Small Number of Views

J. F. Menudet, J. M. Becker, T. Fournel and C. Mennessier

Laboratoire Hubert Curien, UMR CNRS 5516 - Universit

e Jean Monnet, 18 rue Pr Beno

ıt Lauras, Saint-Etienne, France

Keywords:

Visual Hull, Shape From Silhouette, Contour, Radial Basis Function, Deformable Model, Non-Rigid Regis-

tration.

Abstract:

This article presents a model-based approach to Shape From Silhouette reconstruction. It is formulated as a

problem of 3D-2D non-rigid registration: a surface model is deformed until it correctly matches the detected

silhouettes in the images. An efﬁcient and reliable solution is proposed, based on a Radial Basis Function

deformation driven by control points located on the contour generators of the 3D model. Unlike previous

methods relying on non-linear optimization techniques, the proposed method only requires a linear system

solving. Another advantage of this model-based approach is to produce a surface representation of the visual

hull. Moreover, the introduction of shape priors allows to reduce in a dramatic way the number of views

required to obtain a realistic reconstruction. Application to human body modeling is given.

1 INTRODUCTION

Image-based modeling aims at the acquisition of a 3D

model from multiple images of a real world object. It

is a simple and low cost approach compared to other

methods such as laser scanner or structured-light pro-

jection. Some examples of image-based modeling

techniques are Structure From Motion (SFM) (Hart-

ley and Zisserman, 2004) and Shape From Shading

(Prados and Faugeras, 2005). Another popular tech-

nique is Shape From Silhouette (SFS) which produces

the visual hull of the object, an outer approximation

of the 3D shape, consistent with a set of silhouettes

detected in several images (Laurentini, 1994). Appar-

ent contours give strong clues about the 3D shape of

an object. Furthermore, they are far more easier to

ﬁnd than point correspondences required for example

in SFM. Nevertheless, the accuracy of the visual hull

is directly related to the number of input images as

well as the different locations of the camera. Another

well-known intrinsic limitation of SFS is the impossi-

bility to reconstruct concavities.

Typically, a good SFS reconstruction requires 15

to 30 views of the object (depending on its complex-

ity), with apparent contours of the object detected in

each view. Automatic detection is possible in some

conditions (almost uniform background) but in most

cases, a human supervision is necessary. Hence, the

number of views is a critical issue, strongly inﬂuenc-

ing the overall processing time. An efﬁcient and ac-

curate SFS method with a small number of views is

therefore highly desirable.

When less data is available, the inherent loss of ac-

curacy can be compensated by a priori knowledge as

accounted for in inverse problems literature. If the ob-

ject to reconstruct is not totally unknown, SFS could

also beneﬁt from this approach. The principle of a

deformable model is precisely well suited to incorpo-

rate shape prior. For example, the human body topol-

ogy is always the same and its shape is approximately

known a priori. A generic model is therefore easy to

construct. The main problem is the expression of the

model deformation to match the data, i.e. the apparent

contours in the context of SFS.

The method presented in this article is space de-

formation driven by silhouettes’ ﬁtting: the projec-

tion of the model after this deformation should coin-

cide exactly with the silhouettes. Our main contri-

bution is a linear solution to the underlying problem

of 3D/2D non-rigid registration, unlike prior works

379

F. Menudet J., M. Becker J., Fournel T. and Mennessier C. (2007).

MODEL-BASED SHAPE FROM SILHOUETTE - A Solution Involving a Small Number of Views.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 379-386

 SciTePress

based on non-linear optimization framework. It is

therefore an efﬁcient and reliable (no local minima)

technique. This is achieved by the displacements of

some control points located on the contour generators

of the surface model. Radial Basis Function (RBF) is

then used to construct a space deformation interpolat-

ing these displacements. A special case of RBF de-

formation is the Thin Plate Spline warping presented

in (Bookstein, 1989). In section 2, a review of related

works is presented. Then, section 3 details the differ-

ent steps of the proposed method: computation of the

control points, estimation of their displacements and

construction of the space deformation. Finally, some

results are shown in section 4. We illustrate our ap-

proach throughout the paper with human body mod-

eling, believed to be a relevant and important applica-

tion of our method.

2 RELATED WORK

A large literature covers the problem of the represen-

tation and construction of the visual hull. Two cate-

gories of methods can be distinguished: surface-based

and volume-based approaches. The former is based

on the intersection of the visual cones generated by

the apparent contours. Intuitive at ﬁrst, it is actually

difﬁcult to implement for complex objects but some

efﬁcient algorithms exist for polyhedral reconstruc-

tion (Franco and Boyer, 2003). Because of the com-

plexity of surface-based approach, volumetric recon-

struction is widely used (Szeliski, 1993). The space

of interest is ﬁrst discretized by a voxel representa-

tion. Then, each voxel is projected on the different

image planes and voxels falling completely outside of

any silhouette are removed. This simple approach has

nevertheless some drawbacks. First, a surface repre-

sentation is often preferred (for rendering purpose for

example). Secondly, voxel representation is only an

approximation of the exact visual hull due to quanti-

zation error. Decreasing the voxel size obviously re-

duces the problem at the expense of rapidly growing

computational and storage costs (octree hierarchies

are therefore often used).

Model-based reconstruction of objects has re-

cently received great attention. It has been used to

incorporate complementary data (mainly silhouette

and texture). In (Isidro and Sclaroff, 2003), a sur-

face mesh is iteratively deformed in order to obtain

a photometrically-consistent solution while enforcing

silhouette constraint. A similar snake-like technique

is described in (Hernandez and Schmitt, 2004): the

texture driven force deforming the model is here com-

puted with a multi-stereo correlation voting approach

and a gradient vector ﬂow diffusion (Xu and Prince,

1998). A silhouette force is added to constraint the

model. A method combining explicit (mesh) and im-

plicit (metaball) surface has been proposed in (Ilic and

Fua, 2006): the model is ﬁtted to silhouette and stereo

data with a Dirichlet Free Form Deformation incor-

porated in an optimization scheme. Another solution

(Sullivan and Ponce, 1998) in the case of pure SFS

(when only silhouette data is available) is based on an

initial spline surface deformed to match the silhou-

ette. Again, it relies on an optimization framework

(gradient-descent) subject to local minima and long

computation time. In the ﬁeld of human body mod-

eling, the most closely related work to ours is (Hilton

et al., 2000) which deforms a generic human model in

order that its silhouettes approximate the given ones.

Is is a fast technique but the model deformation is

restricted to afﬁne transformation. Another different

approach is statistical shape model as used in (Fleute

and Lavall

ee, 1999) but the training phase (inherent

to this kind of model) is by itself a problem.

3 MODEL-BASED SHAPE FROM

SILHOUETTE

3.1 Overview of the Proposed Method

The main idea is to compute some control points on

the contour generators of the 3D model and move

them with the objective that their projection match the

silhouettes. RBF ﬁnally provides a smooth deforma-

tion of the 3D space (hence of the embedding model),

based on the displacement of these control points. Re-

call that for a given camera position, a contour gener-

ator (or rim) of a surface

S is the curve on S which

projects to the apparent contour in the image (Rosten

and Drummond, 2003). Moreover, surface normals

along rim curve are orthogonal to the viewing direc-

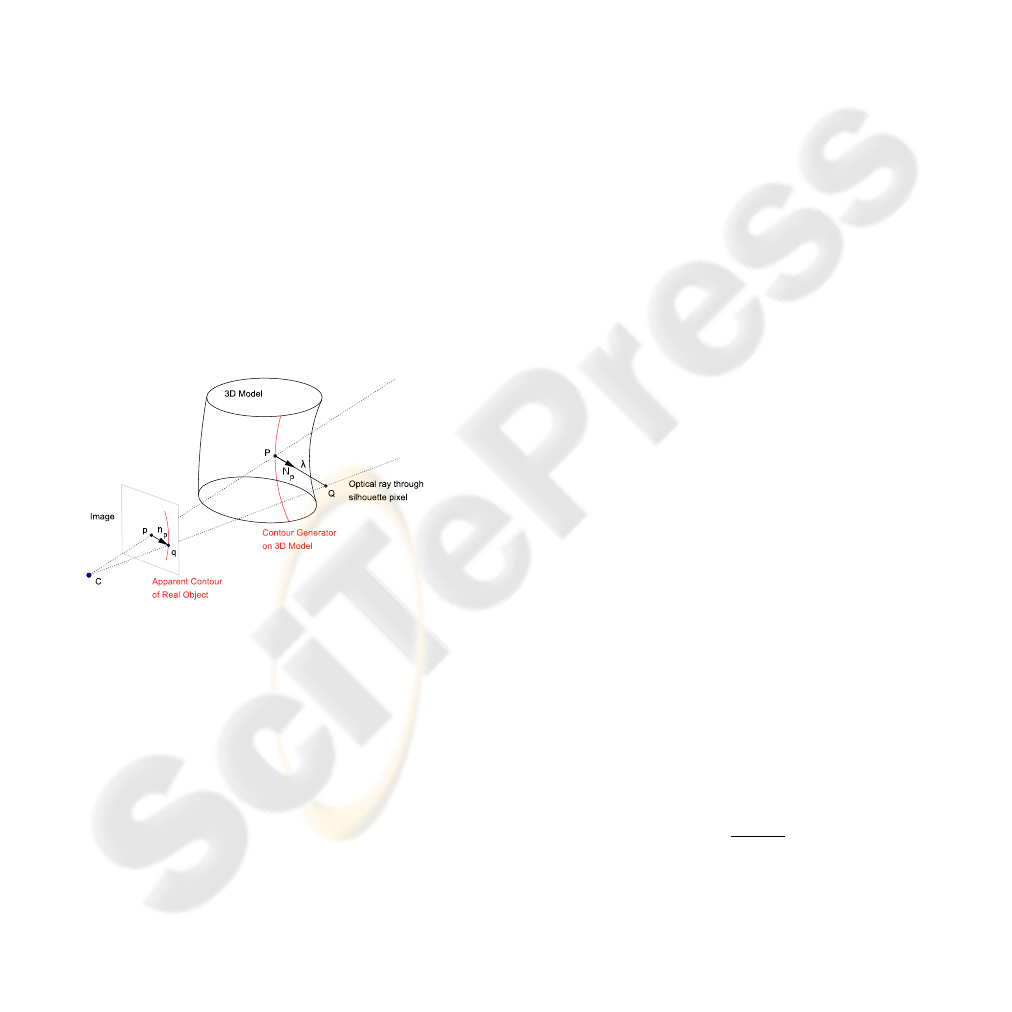
tion (see ﬁgure 1).

Let us now detail the different steps of the pro-

posed method. Apparent contours are assumed de-

tected in calibrated images (Zhang, 2000), i.e. in-

trinsic and extrinsic parameters of the camera are

known. Vectors and matrices are respectively type-

set using bold and sans-serif fonts, e.g. vector P and

matrix K. Vectors are always column vectors such as

P = [X Y Z]

. The cross-product of two 3D vectors is

denoted by × and the symbol ∼ means equality up to

a non zero scale factor.

Figure 1: Contour generator (or rim) on a surface is the

locus of points where surface normal is orthogonal to the

line of sight.

3.2 Initial Registration

The ﬁrst step is a registration of the 3D model in the

world coordinate system. It may be based on few

landmarks (at least 3) located on the model and iden-

tiﬁed in various images. 3D reconstruction of the

image points is possible thanks to the known cam-

era parameters. Finally, a transformation between the

model landmarks and the reconstructed points can be

computed and applied to the model. With 3 land-

marks, only a similarity (rotation, translation plus

scaling) can be estimated. When more landmarks are

available, afﬁne or projective transformation is a valid

alternative, bringing a ﬁrst deformation of the model

in addition to the registration of the coordinate sys-

tems.

3.3 Computation of Control Points on

the 3d Model

We want to place some control points on the rims of

the 3D model. The ﬁrst step is the computation of

the rims, a classical problem occurring for example in

non-photorealistic rendering (Hertzmann and Zorin,

2000). Different techniques have been proposed, de-

pending on the way the surface is represented. Im-

plicit surfaces are probably the most convenient rep-

resentation for rim computation: an efﬁcient algo-

rithm based on the solution of an ordinary differential

equation is available (Rosten and Drummond, 2003).

Nevertheless, implicit surfaces are difﬁcult to render

and their deformation is not intuitive. Surfaces rep-

resented by triangular meshes are therefore preferred

for their versatility and fast rendering ability.

We have adopted the solution presented in (Hertz-

mann, 1999), well suited for triangular meshes rep-

resenting smooth surfaces (via subdivision technique

for example). Let N

be the surface normal at a ver-

tex V of the mesh. Let C be the position of the camera

center. As mentioned above (see ﬁgure 1), rim curve

is the locus of surface points P whose normal is per-

pendicular to the line of sight:

.(P−C) = 0. (1)

For each vertex of the mesh, it is possible to compute

the normalized dot product between surface normal

and viewing direction:

.(V−C)

V−C

. (2)

The surface is assumed continuous, hence if two ver-

tices V

and V

forming an edge of the mesh have

different signs for values d

, then there must be a rim

point on this edge - that is, a zero crossing of the dot

product function (see ﬁgure 2). The location of this

zero crossing along the edge can be estimated with a

linear interpolation between the 2 vertices using val-

ues d

and d

. The rim curve is then constructed by

connecting the rim points located on edges sharing a

common vertex.

Figure 2: The sign of the dot product between surface nor-

mal and viewing direction is computed at each vertex of the

mesh. A change of signs between two adjacent points al-

lows to identify an edge with a rim point (blue circle) which

can be connected to create the rim curve (red line).

This algorithm is applied to the different locations

of the camera. The control points are taken as the vis-

ible rim points previously obtained. Note that only

the visibility of these points has to be checked. It is

signiﬁcantly simpler than the removal of hidden por-

tions of curves, as it would be required in a com-

puter graphics application. The result of this algo-

rithm clearly depends on the resolution of the mesh:

the smaller the triangles, the better the rim estimation

and the higher the number of control points. But in re-

turn, the number of triangles also inﬂuences the com-

putation time. A multi-resolution approach would be

clearly an efﬁcient solution. Subdivision surface pre-

cisely allows to reﬁne locally the mesh around the ini-

tial rim curve. In this way, only edges of the newly

created triangles are tested, speeding up the computa-

tion . This process is repeated until the desired reso-

lution is reached. As will be seen in the sequel (see

section 3.5), a large number of control points (more

than a few thousand) is actually undesirable.

3.4 Estimation of Control Points

Displacements

The present issue is to ﬁnd for every previously com-

puted control point P, the displacement toward the

corresponding point Q. The projection of Q must be

located on the apparent contours, but an inﬁnite num-

ber of points satisfy this constraint. Two observations

will guide us to compute Q:

• Obviously, Q is located on the optical rays passing

through silhouette pixels.

• To ensure a coherent deformation of the model,

control points P should be moved along the sur-

face normal N

. This is a common assumption

(Hernandez and Schmitt, 2004) which has the ad-

vantage to preserve the initial quality of the mesh

(especially an even repartition of its vertices).

Therefore, we propose the following idea to estimate

Q given a rim point P on the 3D model: compute λ

such that the point Q = P+ λN

projects to the appar-

ent contour (see ﬁgure 3).

Figure 3: Estimation of Q, the rim point on the real object

corresponding with the rim point P of the 3D model.

Because the camera is calibrated, coordinates

[X Y Z]

of P are known in the 3D camera frame. For

the same reason, homogeneous coordinates of its pro-

jection p can also be determined from the intrinsic

parameters matrix K (Zhang, 2000):

p = [uv1]

∼ KP. (3)

λ can be computed in two steps:

1. Starting from the point p in image, ﬁnd the point

q = [u

′

on apparent contour situated in the

direction of n

(the projection of N

2. Solve for λ the equation

K(P+ λN

) ∼ q (4)

which can be rewritten

K(P+ λN

) ×q ∼p×q+ λn

×q = 0, (5)

giving 3 scalar equations for ﬁnding λ. One of

them may be preferred to avoid the smallest com-

ponents of n

×q.

3.5 Space Deformation

3.5.1 Problem Statement

The previous steps deﬁne only the displacements

→Q

of N control points whereas a deformation of

space is required: an underlying R

→ R

mapping

S(P) = [s

(P) s

(P)]

(6)

has to be estimated. It would allow to interpolate the

displacement of any 3D point, especially those of the

3D model. The problem is to ﬁnd the three R

→ R

interpolant functions (s

, s

) such that

) = Q

for i = 1, ..., N (7)

) = Q

with Q





. There are obviously an inﬁ-

nite number of functions verifying the interpolation

conditions (7). The problem is to ﬁnd the “best one”.

3.5.2 Radial Basis Function Interpolation

Radial Basis Function (RBF) is a popular technique

to solve this problem of scattered data interpolation

(Carr et al., 2003). In general, suppose that the val-

ues f

of a R

→ R function f are known at N arbi-

trary points c

∈ R

: the problem is to ﬁnd an inter-

polant function s(x) such that s(c

) = f

= f(c

) for

i = 1, ..., N. A RBF is a function s of the form

s(x) = p(x) +

∑

i=0

φ(

x−c

) (8)

where p(x) is a polynomial with a low degree m and

φ(r) is the basis function deﬁned for r ∈[0, +∞[. The

’s and c

’s are respectively the weights and the cen-

ters of the RBF. Some common RBFs are:

• gaussian: φ(r) = e

−cr

(and optional polynomial)

• multiquadric: φ(r) =

√

+ c

with p(x) = a

• thin-plate spline (d=2): φ(r) = r

ln(r) with

p(x) = a

+ a

x+ a

• biharmonic spline (d=3): φ(r) = r with p(x) =

+ a

x+ a

y+ a

• triharmonic spline (d=3): φ(r) = r

with p(x) a

trivariate quadratic polynomial

Depending on the choice of φ and p, the resulting

function s will have different properties. For exam-

ple, splines give smooth interpolant functions because

they minimize energy in second (thin-plate, bihar-

monic) or third (triharmonic) derivative of s (Book-

stein, 1989; Carr et al., 2003). Note also that a closely

related technique to RBF is kriging with spline in-

terpolation as a special case (Trochu, 1993). Mainly

used in geostatistics, its goal is to ﬁnd the best linear

unbiased estimator of a random function (best means

with minimal variance). Interestingly, in this frame-

work, the basis functions φ are interpreted as a spatial

correlation between the data which yields some in-

sights on their choice.

The interpolation problem is reduced now to the

computation of the weights w = [w

... w

]

and coef-

ﬁcients a = [a

... a

]

p(x) = a

(x) + ... + a

(x) (9)

where {p

, ..., p

}is a basis for polynomials of degree

at most m (for example {1, x, y} in the case of the 2D

thin-plate spline). Let f be the vector [ f

... f

]

, Φ the

N ×N matrix with Φ

= φ(



−c



) and P the N ×k

matrix with P

= p

). The interpolation conditions

can then be rewritten in matrix form:



Φ P







= f. (10)

This system is underdetermined (N+k unknowns and

N equations). Therefore, the so-called “side condi-

tions” are imposed on w to ensure that the transfor-

mation has square integrable second derivatives:

w = 0. (11)

(10) and (11) can be gathered into the following

symmetric linear system:



Φ P









. (12)

The weights w and polynomial coefﬁcients a are

the solution of (12) and completely deﬁne the inter-

polant function s(x). The different choices of φ(r)

and p(x) presented above guarantee an invertible sys-

tem under very mild conditions on the centers’ lo-

cations (not aligned for thin-plate spline while gaus-

sian and multiquadric place no restrictions). Never-

theless, using a large number of data points can even-

tually give rise to a ill-conditioned matrix in equation

(12). Moreover, basis functions with non-compact

support (e.g. polyharmonic splines) yield a dense sys-

tem whose solution requires

O (N

) operations.

3.5.3 Radial Basis Function Deformation

As said before, we are looking for 3 functions (s

, s

) describing a space deformation. These 3 RBFs

share the same centers (namely the N control points

), hence the matrix of system (12) is identical for the

3 functions which saves computation time. Because a

smooth transformation is desired, biharmonic or tri-

harmonic splines seem appropriate. The latter have

been used in free-form modeling because of their pre-

dictable and intuitive behavior (Botsch and Kobbelt,

2005). We adopt it for the same reason, using gener-

ally less than 1000 control points.

An interesting variant of the interpolation prob-

lem comes from the introduction of a regularization

term (i.e. smoothing), yielding approximation rather

than interpolation. It may be a better choice when the

reliability of the control points is low. The solution

to this approximation scheme is very similar to the

interpolation one: the only modiﬁcation is the addi-

tion of a parameter λ in the diagonal of the matrix Φ

which is therefore replaced by Φ + λI. The parame-

ter λ controls the smoothness of the transformation:

with λ = 0, we obtain the interpolant transformation

whereas higher values of λ bring smoother transfor-

mations, until the weights w vanish when λ →∞ (sim-

ple polynomial transform, e.g. afﬁne).

3.5.4 Progressive Deformation

The proposed deformation scheme relies on the fun-

damental assumption that the deformed rims coincide

with the rims of the transformed model. This assump-

tion looks very reasonable because the deformation is

smooth and normal to the surface. However, it is not

strictly true, especially when a large deformation is

applied. In other words, the rims computed after the

model deformation may not be projected exactly on

the apparent contours in images. This drawback oc-

curs especially when the initial model is far from the

real object. Moreover, in this case the computed rim

points are usually misplaced on the initial surface, i.e.

they do not correspond with the apparent contours of

the real object. It can generate some artifacts in the

space deformation.

We overcome both problems with a progressive

and regularized space deformation. It is achieved with

successive RBF deformations steered by a decreasing

smoothing parameter λ. After each deformation, con-

trol points and their displacements are recomputed.

Therefore, their reliability increases as the surface is

getting closer to the target shape, justifying the pro-

gressive decrease of λ. At the last step, λ is set to

0 to obtain exact interpolation. In our current imple-

mentation, the number of steps (namely 6) and the

successive values of λ are ﬁxed a priori; afﬁne trans-

formation (λ → ∞) is forced during the ﬁrst 2 iter-

ations, then λ = (1, 0.1, 0.01, 0) for the last 4 steps.

Note that these values are related to the overall size of

the model. Here, the control points are scaled to ﬁt in

a unit cube before forming the RBF system.

4 APPLICATION TO HUMAN

BODY MODELING

4.1 Experimental Setup

We demonstrate an application of our method with the

modeling of a mannequin female torso based on only

4 images (see ﬁgure 4). These images (1600×1200

pixels) were acquired with a digital still camera. The

photographs are only taken from the right side and

front side of the dummy. The apparent contours in the

different views are found in a semi-automatic way:

an initial contour is hand drawn, then deformed using

a snake method (Xu and Prince, 1998). All images

are calibrated using a plane-based calibration method

(Zhang, 2000) (calibration grid not shown in images).

4.2 Initialization

We use a generic model of female torso, represented

by a mesh of 9000 triangles. The initial afﬁne reg-

istration of this model (see section 3.2) is computed

by pointing at 4 anatomical landmarks in the images

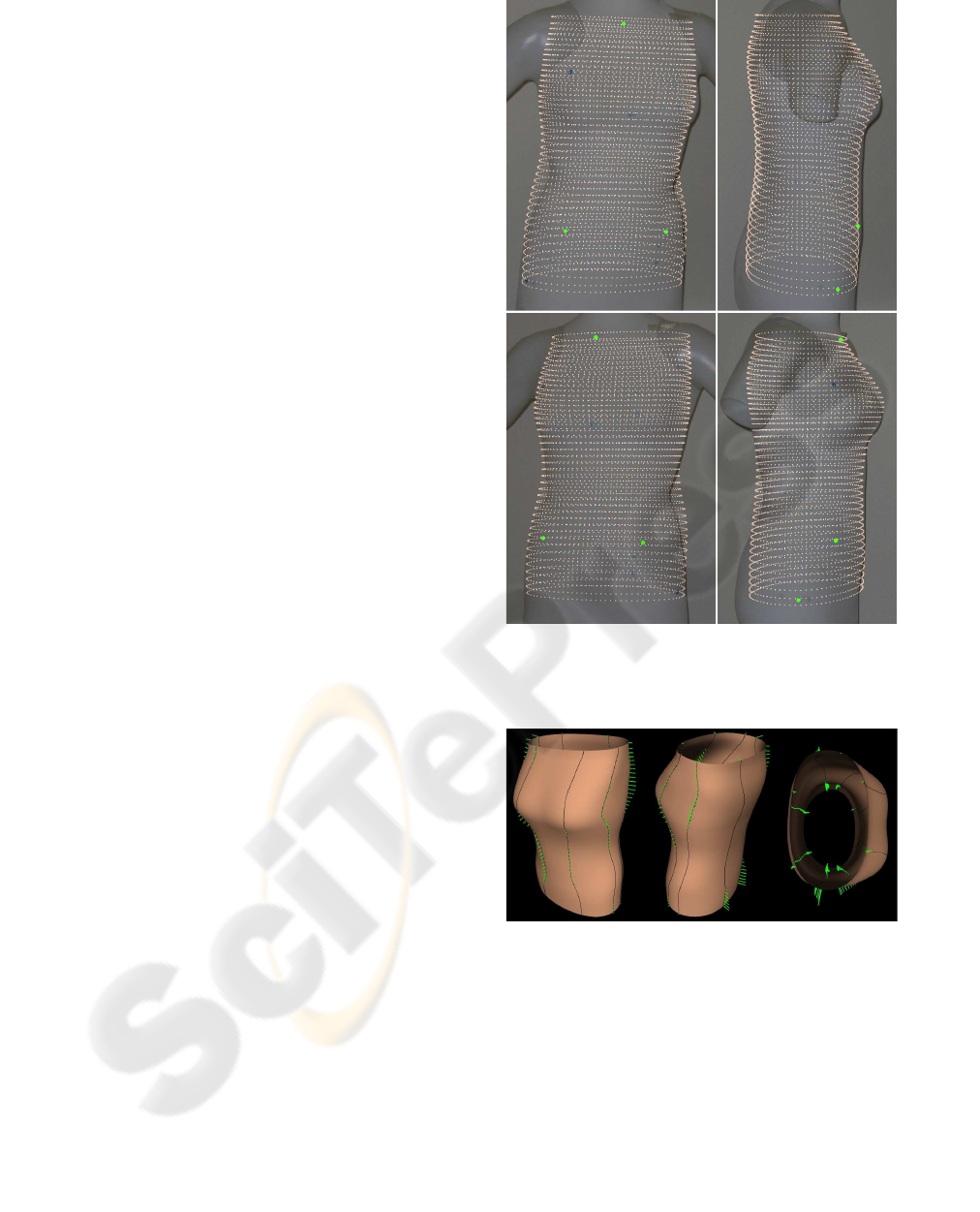
(seen as green dots in ﬁgure 4). Several views of the

3D model after this ﬁrst registration step are presented

in the ﬁgure 5. The projection in the images of the

model vertices is shown in ﬁgure 4. At this step, vol-

ume, position and orientation of the model are rather

good but the matching of silhouettes is not respected.

Especially, breast, waist and spinal shapes are not co-

herent with the images.

4.3 Results

The rim curves are computed on the initial surface

model (black curves in ﬁgure 5), according to the

calibration parameters. The same ﬁgure shows the

displacements of 344 control points estimated from

the apparent contours (green segments). The control

points are well distributed all around the shape though

the photographs are taken from restricted viewpoints.

The displacement of the control points can be signiﬁ-

cant in some areas (up to 4 cm).

The progressive deformation described previously

is ﬁnally applied. The resulting surface model after

space deformation is presented in ﬁgure 6 and its pro-

jection in the 4 images is shown in ﬁgure 7. Note

how the model perfectly matches the silhouettes (es-

pecially the shape of the waist). Nevertheless, the pro-

jection of the ﬁnal model in two images not used in

Figure 4: The 4 images of a dummy torso with the anatomi-

cal landmarks used to compute the initial registration (green

dots). Projection of the initial model is superimposed.

Figure 5: Three different views of the initial 3D model. The

computed rim curves are shown in black. The green seg-

ments represent the displacements of control points used to

computed the RBF deformation.

the deformation reveals some differences (especially

around the right shoulder blade) between the recon-

structed and the actual shape (see ﬁgure 8). Indeed,

deformable model method is obviously not a com-

plete substitute for image data that could give, for ex-

ample, the shape of the shoulder blade. Accuracy has

been manually assessed by measuring some circum-

ferences on both real object and 3D model. A 3%

relative mean error of has been found, probably due

to camera parameters and manual measurements un-

certainties.

The computation time is only 3 seconds on a com-

puter equipped with a P4 3GHz processor and 1024

MB of RAM. This time is based on a basic C++ im-

plementation, but there is a lot of place for improve-

ment of speed. The most time consuming tasks are

rims computation and RBF system solving. In both

cases, more efﬁcient algorithms are available (Hertz-

mann and Zorin, 2000; Botsch and Kobbelt, 2005).

Figure 6: Different views of the ﬁnal 3D model, i.e. after

the space deformation.

4.4 Inﬂuence of the Initial Model

In another experiment, the generic female torso model

has been replaced by a cylinder. The goal is to evalu-

ate the inﬂuence of the initial surface. The 3D shape

obtained after deformation is shown in ﬁgure 9. The

ﬁnal result is globally similar to the previous surface

and its projection in images still matches the appar-

ent contours. The main problem is the shape of the

chest which is not satisfying, especially the loss of

the concave part between the breasts. However, this

is not surprising since it is a well-known limitation

of SFS. The resulting shape is however rather accept-

able, given the small number of images. It conﬁrms

that our model-based SFS is able to bring a signiﬁ-

cant improvement of quality when the model is well

chosen.

5 CONCLUSION

A model-based Shape From Silhouette technique has

been presented. The result is a surface representa-

tion of the visual hull, more convenient than volu-

metric representation. Moreover, the introduction of

a shape prior allows to reduce the number of input

images while keeping a good reconstruction quality.

Figure 7: Projection in the images of the ﬁnal 3D model.

Figure 8: Projection of the ﬁnal 3D model in two additional

images, not used during the deformation.

Our main contribution is a reliable and efﬁcient so-

lution to the underlying problem of 3D/2D non-rigid

registration between the 3D model and the 2D silhou-

ettes. The core idea is that the apparent contours give

sufﬁcient strong clues to construct a progressive de-

formation of space based on Radial Basis Function.

Figure 9: The 3D shape obtained from the deformation of a

cylinder.

Unlike previous works, the method does not use

non-linear optimization strategies: a simple linear

system has to be solved. Efﬁciency is closely con-

nected with the size of this system, i.e. the number

of control points used to drive the deformation. Our

method is clearly intended for smooth objects, hence

a few hundred of control points are sufﬁcient. An-

other factor inﬂuencing the computation time is the

number of images but the method is designed to keep

it small. The main limitations are the availability of

a generic 3D model of the object and the requirement

of some landmarks for the initial registration. A point

to improve is the decreasing scheme of the smoothing

parameter used in the deformation. We plan to ﬁnd

a dynamic adjustment of this sequence, based on an

analysis of the displacements of control points.

Human body is a good subject for our method.

We have demonstrated the modeling of a human torso

with as few as 4 images. A classical SFS technique

would need at least 20 images to produce such a re-

alistic 3D model. The next step is the modeling of

the whole body. The work presented in (Hilton et al.,

2000) may, for example, be adapted to ﬁt our ap-

proach. A lot of applications in medical, garment or

virtual reality ﬁelds would be possible.

REFERENCES

Bookstein, F. (1989). Principal warps: thin-plate splines

and the decomposition of deformations. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

11(6):567–585.

Botsch, M. and Kobbelt, L. (2005). Real-time shape editing

using radial basis functions. In Eurographics05.

Carr, J., Beatson, R., McCallum, B., Fright, W., McLennan,

T., and Mitchell, T. (2003). Smooth surface recon-

struction from noisy range data. In International Con-

ference on Computer Graphics and Interactive Tech-

niques in Australasia and South East Asia (Graphite

2003).

Fleute, M. and Lavall

ee, S. (1999). Nonrigid 3-d/2-d regis-

tration of images using statistical models. In MICCAI,

pages 138–147.

Franco, J. and Boyer, E. (2003). Exact polyhedral visual

hulls. In British Machine Vision Conference.

Hartley, R. and Zisserman, A. (2004). Multiple View Geom-

etry In Computer Vision. Cambridge University Press,

second edition.

Hernandez, C. and Schmitt, F. (2004). Silhouette and stereo

fusion for 3d object modeling. Computer Vision and

Image Understanding, 96(3):367–392.

Hertzmann, A. (1999). Introduction to 3d non-

photorealistic rendering: Silhouettes and outlines.

In Non-Photorealistic Rendering, ACM SIGGRAPH

Course Notes.

Hertzmann, A. and Zorin, D. (2000). Illustrating smooth

surfaces. In ACM SIGGRAPH 2000.

Hilton, A., Beresford, D., Gentils, T., Smith, R., Sun, W.,

and Illingworth, J. (2000). Whole-body modelling

of people from multi-view images to populate virtual

worlds. Visual Computer: International Journal of

Computer Graphics, 16:411–436.

Ilic, S. and Fua, P. (2006). Implicit meshes for surface re-

construction. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 28(2):328–333.

Isidro, J. and Sclaroff, S. (2003). Stochastic reﬁnement of

the visual hull to satisfy photometric and silhouette

consistency constraints. In IEEE International Con-

ference on Computer Vision, 2003., volume 2, pages

1335–1342.

Laurentini, A. (1994). The visual hull concept for

silhouette-based image understanding. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

16(2):150–162.

Prados, E. and Faugeras, O. (2005). Shape from shading:

a well-posed problem? In IEEE Conference on Com-

puter Vision and Pattern Recognition, volume 2, pages

870–877.

Rosten, E. and Drummond, T. (2003). Rapid rendering

of apparent contours of implicit surfaces for real-time

tracking. In British Machine Vision Conference.

Sullivan, S. and Ponce, J. (1998). Automatic model con-

struction and pose estimation from photographs us-

ing triangular splines. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 20(10):1091–

1097.

Szeliski, R. (1993). Rapid octree construction from image

sequences. CVGIP: Image Understanding, 58(1):23–

32.

Trochu, F. (1993). A contouring program based on dual

kriging interpolation. Engineering with Computers,

9:160–177.

Xu, C. and Prince, J. L. (1998). Snakes, shapes, and gradi-

ent vector ﬂow. IEEE Transactions on Image Process-

ing, 7:359–369.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1330–1334.