
COMPACT (AND ACCURATE) EARLY VISION PROCESSING IN
THE HARMONIC SPACE
Silvio P. Sabatini, Giulia Gastaldi, Fabio Solari
Dipartimento di Ingegneria Biofisica ed Elettronica, University of Genoa, via Opera Pia 11a, Genova, Italy
Karl Pauwels, Marc van Hulle
Laboratorium voor Neuro- en Psychofysiologie, K.U.Leuven, Belgium
Javier D
´
ıaz, Eduardo Ros
Departamento de Arquitectura y Tecnologia de Computadores, University of Granada, Spain
Nicolas Pugeault
School of Informatics, University of Edinburgh, U.K.
Norbert Kr
¨
uger
The Maersk Mc-Kinney Moller Institute, University of Southern Denmark, Odense, Denmark
Keywords:
Phase-based techniques, multidimensional signal processing, filter design, optic flow, stereo vision.
Abstract:
The efficacy of anisotropic versus isotropic filtering is analyzed with respect to general phase-based metrics for
early vision attributes. We verified that the spectral information content gathered through oriented frequency
channels is characterized by high compactness and flexibility, since a wide range of visual attributes emerge
from different hierarchical combinations of the same channels. We observed that it is preferable to construct
a multichannel, multiorientation representation, rather than using a more compact representation based on an
isotropic generalization of the analytic signal. The complete harmonic content is then combined in the phase-
orientation space at the final stage, only, to come up with the ultimate perceptual decisions, thus avoiding
an “early condensation” of basic features. The resulting algorithmic solutions reach high performance in
real-world situations at an affordable computational cost.
1 INTRODUCTION
Although the basic ideas underlying early vision
appear deceptively simple and their computational
paradigms are known for a long time, early vision
problems are difficult to quantify and solve. More-
over, in order to have high algorithmic performance
in real-world situations, a large number of channels
should be integrated with high efficiency. From a
computational point of view, the visual signal should
be processed in a “unifying” perspective that will al-
low us to share the maximum number of resources.
From an implementation point of view, the resulting
algorithms and architectures could fall short of their
expectations when the high demand of computational
resources for multichannel spatio-temporal filtering
of high resolution images conflicts with real-time re-
quirements. Several approaches and solutions have
been proposed in the literature to accelerate the com-
putation by means of dedicated hardware (e.g., see
(Diaz et al., 2006; Kehtarnavaz and Gamadia, 2005)).
Yet, the large number of products that must be com-
puted to calculate each single pixel of each single
frame for a couple of stereo images and at each time
step still represents the main bottleneck. This is par-
ticularly true for stereo and motion problems to con-
213
P. Sabatini S., Gastaldi G., Solari F., Pauwels K., van Hulle M., Díaz J., Ros E., Pugeault N. and Krüger N. (2007).
COMPACT (AND ACCURATE) EARLY VISION PROCESSING IN THE HARMONIC SPACE.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 213-220
Copyright
c
SciTePress

struct 3D representations of the world, for which es-
tablishing image correspondences in space and space-
time is a prerequisite, but also their most challenging
part.
In this paper, we propose (1) to define a systematic
approach to obtain a “complete” harmonic analysis of
the visual signal and (2) to integrate efficient multi-
channel algorithmic solutions to obtain high perfor-
mance in real-world situations, and, at the same time,
an affordable computational load.
2 MULTICHANNEL BANDBASS
REPRESENTATION
An efficient (internal) representation is necessary to
guarantee all potential visual information can be made
available for higher level analysis. At an early level,
feature detection occurs through initial local quanti-
tative measurements of basic image properties (e.g.,
edge, bar, orientation, movement, binocular disparity,
colour) referable to spatial differential structure of the
image luminance and its temporal evolution (cf. lin-
ear cortical cell responses). Later stages in vision can
make use of these initial measurements by combin-
ing them in various ways, to come up with categor-
ical qualitative descriptors, in which information is
used in a non-local way to formulate more global spa-
tial and temporal predictions. The receptive fields of
the cells in the primary visual cortex have been in-
terpreted as fuzzy differential operators (or local jets
(Koenderink and van Doorn, 1987)) that provide reg-
ularized partial derivatives of the image luminance in
the neighborhood of a given point x = (x, y), along
different directions and at several levels of resolution,
simultaneously. Given the 2D nature of the visual sig-
nal, the spatial direction of the derivative (i.e., the ori-
entation of the corresponding local filter) is an impor-
tant “parameter”. Within a local jet, the directionally
biased receptive fields are represented by a set of sim-
ilar filter profiles that merely differ in orientation.
Alternatively, considering the space/spatial-
frequency duality (Daugman, 1985), the local jets
can be described through a set of independent spatial-
frequency channels, which are selectively sensitive
to a different limited range of spatial frequencies.
These spatial-frequency channels are equally apt as
the spatial ones. From this perspective, it is formally
possible to derive, on a local basis, a complete
harmonic representation (phase, energy/amplitude,
and orientation) of any visual stimulus, by defining
the associated analytic signal in a combined space-
frequency domain through filtering operations with
complex-valued band-pass kernels. Formally, due to
the impossibility of a direct definition of the analytic
signal in two dimensions, a 2D spatial frequency
filtering would require an association between spatial
frequency and orientation channels. Basically, this
association can be handled either (1) ‘separately’,
for each orientation channel, by using Hilbert pairs
of band-pass filters that display symmetry and
antisymmetry about a steerable axis of orientation,
or (2) ‘as-a-whole’, by introducing a 2D isotropic
generalization of the analytic signal: the monogenic
signal (Felsberg and Sommer, 2001), which allows us
to build isotropic harmonic representations that are
independent of the orientation (i.e., omnidirectional).
By definition, the monogenic signal is a 3D phasor
in spherical coordinates and provides a framework
to obtain the harmonic representation of a signal
respect to the dominant orientation of the image that
becomes part of the representation itself.
In the first case, for each orientation channel θ, an
image I(x) is filtered with a complex-valued filter:
f
θ
A
(x) = f
θ
(x) − if
θ
H
(x) (1)
where f
θ
H
(x) is the Hilbert transform of f
θ
(x) with re-
spect to the axis orthogonal to the filter’s orientation.
This results in a complex-valued analytic image:
Q
θ
A
(x) = I ∗ f
θ
A
(x) = C
θ
(x) + iS
θ
(x) , (2)
where C
θ
(x) and S
θ
(x) denote the responses of the
quadrature filter pair. For each spatial location,
the amplitude ρ
θ
=
q
C
2
θ
+ S
2
θ
and the phase φ
θ
=
arctan(S
θ
/C
θ
) envelopes measure the harmonic infor-
mation content in a limited range of frequencies and
orientations to which the channel is tuned.
In the second case, the image I(x) is filtered with
a spherical quadrature filter (SQF):
f
M
(x) = f(x) −(i, j) · f
R
(x) (3)
defined by a rotation invariant even f(x) filter)
and a vector-valued isotropic odd filter f
R
(x) =
( f
R ,1
(x), f
R ,2
(x))
T
, obtained by the Riesz transform
of f(x) (Felsberg and Sommer, 2001). This results in
a monogenic image:
Q
M
(x) = I ∗ f
M
(x) = C(x) + (i, j)S(x) (4)
= C(x) + iS
1
(x) + jS
2
(x)
where, using the standard spherical coordinates,
C(x) = ρ(x)cosϕ(x)
S
1
(x) = ρ(x)sinϕ(x) cosϑ(x)
S
2
(x) = ρ(x)sinϕ(x) sinϑ(x) .
The amplitude of the monogenic signal is the vec-
tor norm of f
M
: ρ =
q
C
2
+ S
2
1
+ S
2
2
, as in the case

of the analytic signal, and, for an intrinsically one-
dimensional signal, ϕ and ϑ are the dominant phase
and the dominant orientation, respectively.
In this work, we want to analyze the efficacy of
the two approaches in obtaining a complete and ef-
ficient representation of the visual signal. To this
end, we consider, respectively, a discrete set of ori-
ented (i.e., anisotropic) Gabor filters and a triplet of
isotropic spherical quadrature filters defined on the
basis of the monogenic signal. Moreover, as a choice
in the middle between the two approaches, we will
also take into consideration the classical steerable fil-
ter approach (Freeman and Adelson, 1991) that allows
a continuous steerability of the filter respect to any
orientation. In this case, the number of basis kernels
to compute the oriented outputs of the filters depends
on the derivative order (n) of a Gaussian function. The
basis filters corresponding to n = 2 or n = 4 turned out
as an acceptable compromise between the representa-
tion efficacy and the computational efficiency.
For all the filters considered, we chose the de-
sign parameters to have a good coverage of the space-
frequency domain and to keep the spatial support (i.e.,
the number of taps) to a minimum, in order to cut
down the computational cost. Therefore, we deter-
mined the smallest filter on the basis of the highest al-
lowable frequency without aliasing, and we adopted
a pyramidal technique (Adelson et al., 1984) as an
economic and efficient way to achieve a multireso-
lution analysis (see also Section 3.2). Accordingly,
we fixed the maximum radial peak frequency (ω
0
)
by considering the Nyquist condition and a constant
relative bandwidth of one octave (β = 1), that al-
lows us to cover the frequency domain without loss
of information. For Gabor and steerable filters, we
should also consider the minimum number of ori-
ented filters to guarantee a uniform orientation cov-
erage. This number still depends on the filter band-
width and it is related to the desired orientation sen-
sitivity of the filter (e.g., see (Daugman, 1985; Fleet
and Jepson, 1990)); we verified that, under our as-
sumptions, it is necessary to use at least eight orien-
tations. To satisfy the quadrature requirement all the
even symmetric filters have been “corrected” to can-
cel the DC sensitivity. The monogenic signal has been
constructed from a radial bandpass filter obtained by
summing the corrected bank of oriented even Gabor
filters. All the filters have been normalized prior to
their use in order to have constant unitary energy. A
detailed description of the filters used can be found at
www.pspc.dibe.unige.it/VISAPP07/
.
3 PHASE-BASED EARLY VISION
ATTRIBUTES
3.1 Basic Principles
During the last decades, the phase from local band-
pass filtering has gained increasing interest in the
computer vision community and has led to the de-
velopment of a wide number of phase-based feature
detection algorithms in different application domains
(Sanger, 1988; Fleet et al., 1991; Fleet and Jepson,
1990; Fleet and Jepson, 1993; Kovesi, 1999; Gau-
tama and Van Hulle, 2002). Yet, to the best of our
knowledge, a systematic analysis of the basic descrip-
tive properties of the phase has never been done. One
of the key contributions of this paper is the formu-
lation a single unified representation framework for
early vision grounded on a proper phase-based met-
rics. We verified that the resulting representation
is characterized by high compactness and flexibility,
since a wide range of visual attributes emerges from
different hierarchical combinations of the same chan-
nels. The harmonic representation will be the base
for a systematic phase-based interpretation of early
vision processing, by defining perceptual features on
measures of phase properties. From this perspective,
edge and contour information can come from phase-
congruency, motion information can be derived from
the phase-constancy assumption, while matching op-
erations, such as those used for disparity estimation,
can be reduced to phase-difference measures. In this
way, simple local relational operations capture signal
features, which would be more complex and less sta-
ble if directly analysed in the spatio-temporal domain.
Contrast direction and orientation. Traditional
gradient-based operators are used to detect sharp
changes in image luminance (such as step edges), and
hence are unable to properly detect and localize other
feature types. As an alternative, phase information
can be used to discriminate different features in a con-
trast independent way, by searching for patterns of or-
der in the phase component of the Fourier transform
(Owens, 1994). Abrupt luminance transitions, as in
correspondence of step edges and line features are, in-
deed, points where the Fourier components are max-
imally in phase. Therefore, both they are signaled by
peaks in the local energy, and the phase information
can be used to discriminate among different kinds of
contrast transition (Kovesi, 1999), e.g., a phase of π/2
corresponds to a dark-bright edge, whereas a phase of
0 corresponds to a bright line on dark background (see
also (Kr
¨
uger and Felsberg, 2003)) .

Binocular disparity. In a first approximation, the
phase-based stereopsis defines the disparity δ(x) as
the one-dimensional shift necessary to align, along
the direction of the (horizontal) epipolar lines, the
phase values of bandpass filtered versions of the
stereo image pair I
R
(x) and I
L
(x) = I
R
[x + δ(x)]
(Sanger, 1988). Formally,
δ(x) =
⌊φ
L
(x) − φ
R
(x)⌋
2π
ω(x)
=
⌊∆φ(x)⌋
2π
ω(x)
(5)
where ω(x) is the average instantaneous frequency of
the bandpass signal, at point x, that, under a linear
phase model, can be approximated by ω
0
(Fleet et al.,
1991). Equivalently, the disparity can be directly ob-
tained from the principal part of phase difference,
without explicit manipulation of the left and right
phase and without incurring the ‘wrapping’ effects on
the resulting disparity map (Solari et al., 2001):
⌊∆φ⌋
2π
= ⌊arg(Q
L
Q
∗R
)⌋
2π
(6)
where Q
∗
denotes complex conjugate of Q.
Normal Flow. Considering the conservation prop-
erty of local phase measurements (phase constancy),
image velocities can be computed from the tempo-
ral evolution of equi-phase contours φ(x,t) = c (Fleet
et al., 1991). Differentiation with respect to t yields:
∇φ· v+ φ
t
= 0 , (7)
where ∇φ = (φ
x
,φ
y
) is the spatial and φ
t
is the tem-
poral phase gradient. Note that, due to the aperture
problem, only the velocity component along the spa-
tial gradient of phase can be computed (normal flow).
Under a linear phase model, the spatial phase gradi-
ent can be substituted by the radial frequency vector
ω = (ω
x
,ω
y
). In this way, the component velocity
v
c
can be estimated directly from the temporal phase
gradient:
v
c
= −
φ
t
ω
0
·
ω
|ω|
. (8)
The temporal phase gradient can be obtained by fit-
ting a linear model to the temporal sequence of spatial
phases (using e.g. five subsequent frames) (Gautama
and Van Hulle, 2002):
(φ
t
, p) = argmin
φ
t
,p
∑
t
(φ
t
·t + p) − φ(t)
2
, (9)
where p is the intercept.
Motion-in-depth. The perception of motion in the
3D space relates to 2nd-order measures, which can
be gained either by interocular velocity differences or
temporal variations of binocular disparity (Harris and
Watamaniuk, 1995). Recently (Sabatini et al., 2003),
it has been proved that both cues provide the same
information about motion-in-depth (MID), when the
rate of change of retinal disparity is evaluated as a
total temporal derivative of the disparity:
dδ
dt
≃
∂δ
∂t
=
φ
L
t
− φ
R
t
ω
0
≃ v
R
− v
L
, (10)
where v
R
and v
L
are the velocities along the epipolar
lines. Through the chain rule in the evaluation of the
temporal derivative of phases, we obtain information
about MID directly from convolutions Q of stereo im-
age pairs and by their temporal derivatives Q
t
, eluding
explicit calculation and differentiation of phase and
the attendant problem of phase unwrapping:
∂δ
∂t
=
Im[Q
L
t
Q
∗L
]
|Q
L
|
2
−
Im[Q
R
t
Q
∗R
]
|Q
R
|
2
1
ω
0
. (11)
3.2 Channel interactions
The harmonic information made available by the dif-
ferent basis channels must be properly integrated
across both multiple scales and multiple orientations
to optimally detect and localise different features at
different levels of resolution in the visual signal.
In general, for what concerns the scale, a multires-
olution analysis can be efficiently implemented by
a coarse-to-fine strategy that helps us to deal with
large features values, which are otherwise unmeasur-
ables by the small filters we have to use in order to
achieve real-time performance. Specifically, a coarse-
to-fine Gaussian pyramid (Adelson et al., 1984) is
constructed, where each layer is separate by an octave
scale. Accordingly, the image is increasingly blurred
with a Gaussian kernel g(x) and subsampled:
I
k
(x) = (
S (g∗ I
k−1
))(x) . (12)
At each pyramid level k the subsampling operator
S
reduces to a half the image resolution respect to the
previous level k − 1. The filter response image Q
k
at
level k is computed by filtering the image I
k
with the
fixed kernel f(x):
Q
k
(x) = ( f ∗ I
k
)(x) . (13)
For what concerns the interactions across the ori-
entations a key distinction must be done according
that one uses isotropic or anisotropic filtering.
Isotropic filtering. The monogenic signal directly pro-
vides a
single
harmonic content with respect to the
dominant orientation:
ρ(x)
def
=
q
C
2
(x) + |S(x)|
2
= E (x)
θ(x)
def
= atan2(S
2
(x),S
1
(x)) = ϑ(x)
φ(x)
def
= sign[S(x) · n
ϑ
(x)]atan2(|S(x)|,C(x)) = ϕ(x),
with n
ϑ
(x) = (cosϑ(x),sinϑ(x)) .

Anisotropic filters. Basic feature interpolation mech-
anisms must be introduced. More specifically, if we
name E
q
and φ
q
the “oriented” energy and the “ori-
ented” phase extracted by the filter f
q
steered to the
angle θ
q
= qπ/K, the harmonic features computed
with this filter orientation are:
ρ
q
(x) =
q
C
2
q
(x) + S
2
q
(x) = E
q
(x)
θ
q
(x) =
qπ
K
φ
q
(x) = atan2(S
q
(x),C
q
(x)) .
Under this circumstance, we require to interpolate the
feature values computed by the filter banks in order
to estimate the filter’s output at the proper signal ori-
entation. The strategies adopted for this interpolation
are very different, and strictly depend on the ‘compu-
tational theory’ (in the Marr’s sense (Marr, 1982)) of
the specific early vision problem considered, as it will
be detailed in the following.
Contrast direction and orientation. According to
(Kr
¨
uger and Felsberg, 2004) the phase is used to de-
scribe the local structure of i1D signals in an image.
Therefore, we determine maxima of the local am-
plitude orthogonal to the main orientation with sub–
pixel accuracy and compute orientation and phase in-
formation at this sub-pixel position using bi-linear in-
terpolation in the phase–orientation space. Sub–pixel
accuracy is achieved by computing the center of grav-
ity in a window with size depending on the frequency
level. For the bilinear interpolation we need to take
care of the topology of the orientation–phase space
that has the form of a half–torus. The precision of
sub–pixel accuracy calculation as well as the preci-
sion of the phase estimate depending on the different
harmonic representations is discussed in Section 4.
Binocular disparity. The disparity computation
from Eq. (5) can be extended to two-dimensional fil-
ters at different orientations θ
q
by projection on the
epipolar line in the following way:
δ
q
(x) =
⌊φ
L
q
(x) − φ
R
q
(x)⌋
2π
ω
0
cosθ
q
. (14)
In this way, multiple disparity estimates are obtained
at each location. These estimates can be combined by
taking their median:
δ(x) = median
q∈V(x)
δ
q
(x) , (15)
whereV(x) is the set of orientations where valid com-
ponent disparities have been obtained for pixel x. Va-
lidity can be measured by the filter energy.
A coarse-to-fine control scheme is used to inte-
grate the estimates over the different pyramid levels
(Bergen et al., 1992). A disparity map δ
k
(x) is first
computed at the coarsest level k. To be compatible
with the next level, it must be upsampled, using an
expansion operator
X , and multiplied by two:
d
k
(x) = 2·
X
δ
k
(x)
. (16)
This map is then used to reduce the disparity at level
k + 1, by warping the phase or filter outputs before
computing the phase difference:
δ
k+1
q
(x) =
⌊φ
L
(x) − φ
R
x− d
k
(x)
⌋
2π
ω
0
cosθ
q
+d
k
(x) . (17)
In this way, the remaining disparity is guaranteed to
lie within the filter range. This procedure is repeated
until the finest level is reached.
Optic flow. The reliability of each component ve-
locity can be measured by the mean squared error
(MSE) of the linear fit in Eq. (8) (Gautama and
Van Hulle, 2002). Provided a minimal number of reli-
able component velocities are obtained (threshold on
the MSE), an estimate of the full velocity can be com-
puted for each pixel by integrating the valid compo-
nent velocities (Gautama and Van Hulle, 2002):
v(x) = argmin
v(x)
∑
q∈O(x)
|v
c,q
(x)| − v(x)
T
v
c,q
(x)
|v
c,q
(x)|
2
,
(18)
where O(x) is the set of orientations where valid com-
ponent velocities have been obtained for pixel x. A
coarse-to-fine control scheme, similar to that of Sec-
tion 3.2 is used to integrate the estimates over the dif-
ferent pyramid levels. Starting from the coarsest level
k, the optic flow field v
k
(x) is computed, expanded,
and used to warp the phases or filter outputs at level
k + 1. For more details on this procedure we refer to
(Pauwels and Van Hulle, 2006).
Motion-in-depth. Although the motion-in-depth is
a 2nd-order measure, by exploiting the direct determi-
nation of the temporal derivative of the disparity (see
Eq.11), the binocular velocity along the epipolar lines
can be directly calculated for each orientation chan-
nel, and thence the motion-in-depth:
V
Z
= median
q∈W
L
(x)
v
L
q
(x) − median
q∈W
R
(x)
v
R
q
(x) , (19)
where for each monocular sequence, W(x) is the set
of orientations for which valid components of veloci-
ties have been obtained for pixel x. As in the previous
cases, a coarse-to-fine strategy is adopted to guarantee
that the horizontal spatial shift between two consecu-
tive frames lie within the filter range.
4 RESULTS
We are interested in computing different image fea-
tures with the maximum accuracy and the lower pro-
cessor requirements. The utilization of the different
filtering approaches leads to different computing load
requirements. Focusing on the convolutions opera-
tions on which the filters are based, we have analyzed
each approach to evaluate their complexity. Spherical
filters require three non-separable convolutions oper-
ations, which make this approach quite expensive in
terms of the required computational resources. The
eight oriented Gabor filters requires eight 2-D non
separable convolution but they can be efficiently com-
puted through a linear combination of separable ker-
nels as it is indicated in (Nestares et al., 1998), thus
significantly reducing the computational load. For
steerable filters, quadrature oriented outputs are ob-
tained from the filter bases composed of separable
kernels. The higher is the Gaussian derivative order,
the higher is the number of the basis filters. More
specifically, the number of 1-D convolutions is given
by 4n+ 6 where n is the differentiation order.
Summarizing, the complexity of computing the
harmonic representation with the different set of fil-
ters is summarized in Table 1.
Table 1: Computational costs of convolution operators.
# filters # taps products sums
Gabor 24 11 264 240
s4
22 11 242 220
s2
14 11 154 140
SQF 3 11×11 363 360
The accuracy achieved by the different filters has been
evaluated using synthetic images with well-known
ground-truth feature.
Contrast direction and orientation. We have uti-
lized a synthetic image (see Figure 1) where the fea-
ture type changes from a step edge to a line feature
from top to bottom (Kovesi, 1999). By rotating the
image by stepwise angles in [0,2π), we constructed a
set of test images and measured the contour localiza-
tion accuracy, phase and orientation with the different
approaches, comparing the results with the ground-
truth. In Table 2 the mean errors in localisation, ori-
entation and phase and their standard deviations are
reported. It is worth noting that the features were
extracted with sub-pixel accuracy. We can see that
Gabor and 4th-order steerable filters (s4) produce the
most accurate results for phase and edge localization,
with low variance. Second order steerable filters (s2)
and SQFs seem very noisy in their phase estimation.
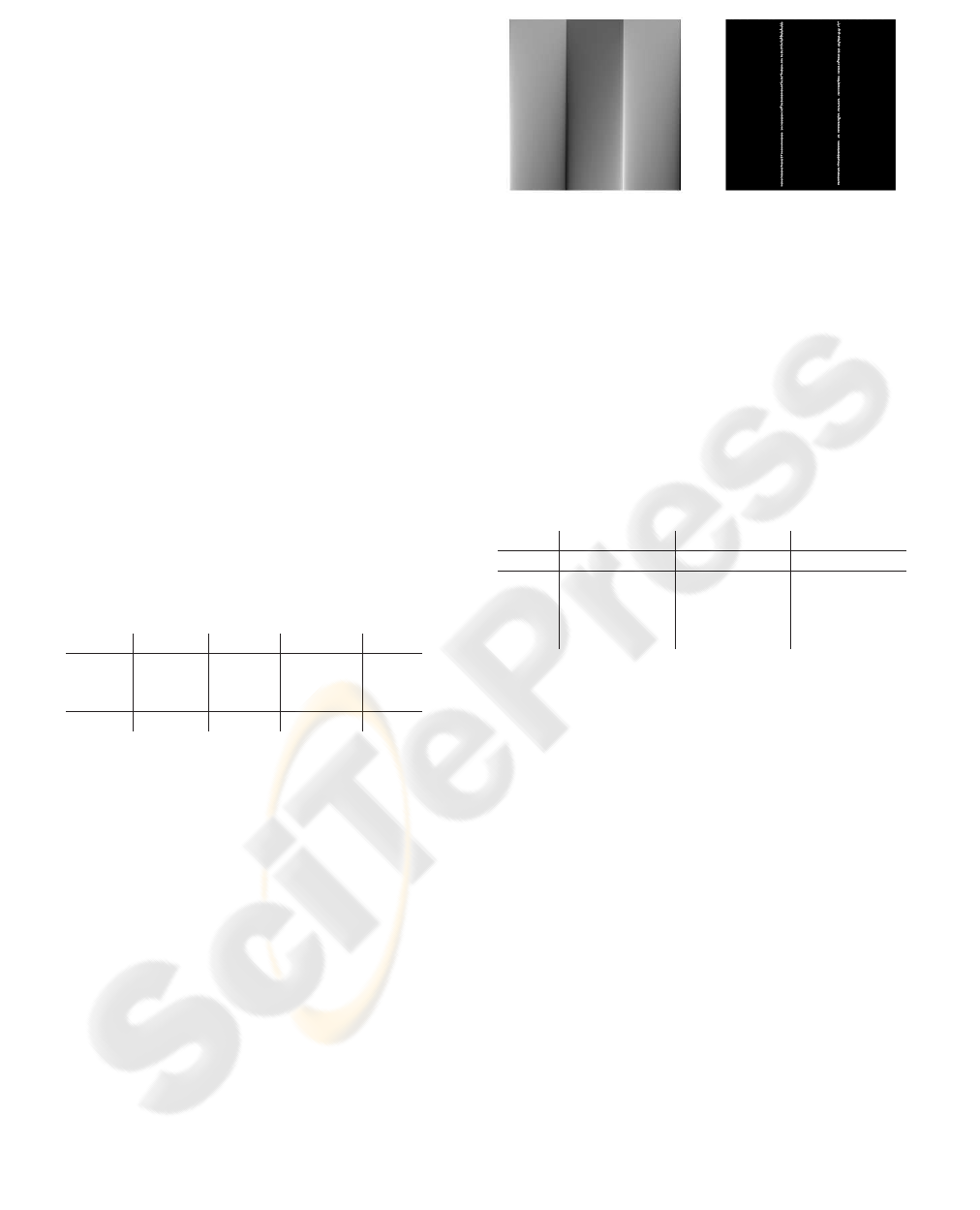
(a) (b)
Figure 1: (a) Test image representing a continuum of
phases taking values in (−π,π] corresponding to a con-
tinuum of oriented grey-level structures as expressed in a
changing “circular” manifold (cf. (Kovesi, 1999)). The
feature type changes progressively from a step edge to a
line feature, while retaining perfect phase congruency. (b)
Phase-based localization of contours obtained by the Gabor
filters.
Table 2: Accuracy evaluation for localization, phase and
orientation in the synthetic image of Figure 1. The localiza-
tion error is expressed in pixels, whereas the orientation and
phase errors are in radians.
localization orientation phase
avg std avg std avg std
Gabor 0.067 0.026 0.021 0.007 0.025 0.005
s4
0.072 0.027 0.022 0.008 0.032 0.006
s2
0.076 0.017 0.042 0.011 0.340 0.203
SQF
0.124 0.062 0.026 0.021 0.198 0.092
Binocular disparity. The tsukuba, sawtooth and
venus stereo-pairs from the Middlebury stereo vision
page (Scharstein and Szeliski, 2002) are used in the
evaluation. Since we are interested in the precision
of the filters we do not use the integer-based mea-
sures proposed there but instead compute the mean
and standard deviation of the absolute disparity er-
ror. To prevent outliers to distort the results, the er-
ror is evaluated only at regions that are textured, non-
occluded and continuous. The best results (see Ta-
ble 3)are obtained with the Gabor filters. Slightly
worse are the results with 4th-order steerable filters
and the 2nd-order filters yield results about twice as
bad as the 4th-order filters. The results obtained with
SQFs are comparable with those obtained by the 2nd-
order steerable filters. Figure 2 contains the left im-
ages of the stereo-pairs, the ground truth depth maps,
and the depth maps obtained with the Gabor filters.
Optic flow. We have evaluated the different filters
with respect to optic flow estimation on the diverg-
ing tree and yosemite sequences from (Barron et al.,
1994), using the error measures presented there. The

Table 3: Average and standard deviation of the absolute er-
rors in the disparity estimates (in pixels).
tsukuba sawtooth venus
avg std avg std avg std
Gabor 0.32 0.61 0.41 1.26 0.25 0.77
s4
0.36 0.68 0.50 1.86 0.40 1.30
s2
0.47 0.79 1.12 2.50 0.98 2.44
SQF
0.46 0.85 0.93 2.20 0.95 2.40
tsukuba sawtooth venus
Figure 2: Left frame (top row), ground truth disparity (mid-
dle row), and estimated disparity using Gabor filters (bot-
tom row).
cloud region was excluded from the yosemite se-
quence. The results are presented in Table 4 and
similar conclusions can be drawn as in the previous
Section. Gabor and 4th-order steerable filters yield
comparable results whereas 2nd-order steerable fil-
ters score about twice as bad. The results obtained by
SQFs are slightly worse, since the resulting optic flow
have larger errors but a higher density. Figure 3 shows
the center images, ground truth optic flow fields, and
the optic flow fields computed with the Gabor filters.
Table 4: Average and standard deviation of the optic flow
errors (in pixels) and optic flow density (in percent).
diverging tree yosemite (no cloud)
avg std dens avg std dens
Gabor 2.05 2.28 95.6 2.15 3.12 81.8
s4
2.39 2.62 93.2 2.96 4.46 85.0
s2
4.20 4.58 90.6 6.51 9.23 81.9
SQF
12.9 13.4 95.1 18.7 17.8 99.1
diverging tree yosemite
Figure 3: Center frame (top row), ground truth optic flow
(middle row) and estimated optic flow obtained with Gabor
filters (bottom row). All optic flow fields have been scaled
and subsampled five times.
Motion-in-depth. Since binocular test sequences
with the ground truth and a sufficiently high frame
rate are not available, it has not been possible to make
quantitative comparisons. However, considering that
motion-in-depth is a ‘derived’ quantity, we expected,
that the multichannel anisotropic filtering has the
same advantages over isotropic filtering alike those
observed for stereo and motion processing. Qualita-
tive results obtained in real-world sequences prelimi-
narily confirmed this conclusion.
5 CONCLUSIONS
Early vision processing can be reconducted to mea-
suring the amount of a particular type of local struc-
ture with respect to a specific representation space.
The choice for an early selection of features by adopy-
ing thresholding procedures, which depend on a spe-
cific and restricted environmental context, limits the
possibility of building, on the ground of such repre-
sentations, an artificial vision system with complex

functionalities. Hence, it is more convenient to base
further perceptual processes on a more general rep-
resentation of the visual signal. The harmonic repre-
sentation discussed in this paper is a reasonable rep-
resentation of early vision process since it allows for
an efficient and complete representation of (spatially
and temporally) localized structures. It is character-
ized by: (1) compactness (i.e., minimal uncertainty
of the band-pass channel); (2) coverage of the fre-
quency domain; (3) robust correspondence between
the harmonic descriptors and the perceptual ‘sub-
stances’ in the various modalities (edge, motion and
stereo). Through a systematic analysis we investi-
gated the advantages of anisotropic
vs
isotropic filter-
ing approaches for a complete harmonic description
of the visual signal. We observed that it is prefer-
able to construct a multichannel, multiorientation rep-
resentation, thus avoiding an “early condensation” of
basic features. The harmonic content is then com-
bined in the phase-orientation space at the final stage,
only, to come up with the ultimate perceptual deci-
sions. An analysis of possible advantages of the ag-
gregation of the information in the monogenic im-
age in mid- and high-level perceptual tasks (e.g., im-
age classification) would require further investigation,
and it is deferred to a future work.
ACKNOWLEDGEMENTS
This work results from a cross-collaborative effort
within the EU Project IST-FET-16276-2 “DrivSco”.
REFERENCES
Adelson, E., Anderson, C., Bergen, J., Burt, P., and Ogden,
J. (1984). Pyramid methods in image processing. RCA
Engineer, 29(6):33–41.
Barron, J., Fleet, D., and Beauchemin, S. (1994). Perfor-
mance of optical flow techniques. Int. J. of Comp.
Vision, 12:43–77.
Bergen, J., Anandan, P., Hanna, K., and Hingorani, R.
(1992). Hierarchical model-based motion estimation.
In Proc. ECCV’92, pages 237–252.
Daugman, J. (1985). Uncertainty relation for resolution in
space, spatial frequency, and orientation optimized by
two-dimensional visual cortical filters. J. Opt. Soc.
Amer. A, A/2:1160–1169.
Diaz, J., Ros, E., Pelayo, F., Ortigosa, E., and Mota, S.
(2006). FPGA based real-time optical-flow system.
IEEE Trans. Circuits and Systems for Video Technol-
ogy, 16(2):274–279.
Felsberg, M. and Sommer, G. (2001). The monogenic sig-
nal. IEEE Trans. Signal Processing, 48:3136–3144.
Fleet, D. and Jepson, A. (1993). Stability of phase in-
formation. IEEE Trans. Pattern Anal. Mach. Intell.,
15(12):1253–1268.
Fleet, D., Jepson, A., and Jenkin, M. (1991). Phase-based
disparity measurement. CVGIP: Image Understand-
ing, 53(2):198–210.
Fleet, D. J. and Jepson, A. D. (1990). Computation of com-
ponent image velocity from local phase information.
Int. J. of Comp. Vision, 1:77–104.
Freeman, W. and Adelson, E. (1991). The design and use
of steerable filters. IEEE Trans. Pattern Anal. Mach.
Intell., 13:891–906.
Gautama, T. and Van Hulle, M. (2002). A phase-based ap-
proach to the estimation of the optical flow field us-
ing spatial filtering. IEEE Trans. Neural Networks,
13(5):1127–1136.
Harris, J. and Watamaniuk, S. N. (1995). Speed discrimina-
tion of motion-in-depth using binocular cues. Vision
Research, 35(7):885–896.
Kehtarnavaz, N. and Gamadia, M. (2005). Real-Time Im-
age and Video Processing: From Research to Reality.
Morgan & Claypool Publishers.
Koenderink, J. and van Doorn, A. (1987). Representation
of local geometry in the visual system. Biol. Cybern.,
55:367–375.
Kovesi, P. (1999). Image features from phase congruency.
Videre, MIT Press, 1(3):1–26.
Kr
¨
uger, N. and Felsberg, M. (2003). A continuous formula-
tion of intrinsic dimension. In Proc. British Machine
Vision Conference, Norwich, 9-11 September 2003.
Kr
¨
uger, N. and Felsberg, M. (2004). An explicit and com-
pact coding of geometric and structural information
applied to stereo matching. Pattern Recognition Let-
ters, 25(8):849–863.
Marr, D. (1982). Vision. New York: Freeman.
Nestares, O., Navarro, R., Portilla, J., and Tabernero, A.
(1998). Efficient spatial-domain implementation of a
multiscale image representation based on Gabor func-
tions. J. of Electronic Imaging, 7(1):166–173.
Owens, R. (1994). Feature-free images. Pattern Recogni-
tion Letters, 15:35–44.
Pauwels, K. and Van Hulle, M. (2006). Optic flow from
unstable sequences containing unconstrained scenes
through local velocity constancy maximization. In
Proc. British Machine Vision Conference, Edinburgh,
4-7 September 2006.
Sabatini, S., Solari, F., Cavalleri, P., and Bisio, G. (2003).
Phase-based binocular perception of motion in depth:
Cortical-like operators and analog VLSI architectures.
EURASIP J. on Applied Signal Proc., 7:690–702.
Sanger, T. (1988). Stereo disparity computation using Ga-
bor filters. Biol. Cybern., 59:405–418.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. Int. J. of Comp. Vision, 47(1–3):7–42.
Solari, F., Sabatini, S., and Bisio, G. (2001). Fast technique
for phase-based disparity estimation with no explicit
calculation of phase. Elect. Letters, 37:1382–1383.
