FAST AND ROBUST IMAGE MATCHING USING CONTEXTUAL

INFORMATION AND RELAXATION

Desire Sidibe, Philippe Montesinos and Stefan Janaqi

LGI2P/EMA - Ales School of Mines, Parc scientiﬁque G. Besse, 30035 Nimes Cedex 1, France

Keywords:

Relaxation, Image matching, Point matching, Scale invariant features.

Abstract:

This paper tackles the difﬁcult, but fundamental, problem of image matching under projective transformation.

Recently, several algorithms capable of handling large changes of viewpoint as well as large scale changes have

been proposed. They are based on the comparison of local, invariants descriptors which are robust to these

transformations. However, since no image descriptor is robust enough to avoid mismatches, an additional step

of outliers rejection is often needed. The accuracy of which strongly depends on the number of mismatches. In

this paper, we show that the matching process can be made robust to ensure a very few number of mismatches

based on a relaxation labeling technique. The main contribution of this work is in providing an efﬁcient and

fast implementation of a relaxation method which can deal with large sets of features. Futhermore, we show

how the contextual information can be obtained and used in this robust and fast algorithm. Experiments with

real data and comparison with other matching methods, clearly show the improvements in the matching results.

1 INTRODUCTION

The problem of ﬁnding correspondences between im-

age features is fundamental in many computer vi-

sion applications such as stereo-vision, image re-

trieval, image registration, robot localization and ob-

ject recognition. Recently, local and invariant fea-

tures have provento be very successful in establishing

image-to-image correspondences. The local charac-

ter yields robutsness to occlusion and varying back-

ground, and invariance makes them robust to scale

and viewpoint changes. Interest points are one of

the most widely used local features. In many appli-

cations, one aims to obtain a set of corresponding

points between two images. Therefore, the extracted

points have to be characterized by a descriptor and

then matched using a similarity measure.

Different methods for detecting invariant features

are proposed (Baumberg, 2000; Mikolajczyk and

Schmid, 2002; Tuytelaars and Van Gool, 2004; Lowe,

1999; Schaffalitzky and Zisserman, 2002; Matas

et al., 2002). Among them, it is worth mention-

ing those based on interest points. (Mikolajczyk and

Schmid, 2002; Mikolajczyk and Schmid, 2004) pro-

pose a scale and afﬁne invariant interest points de-

tector using a scale-space representation of the im-

age. First, points are detected at multiple scales us-

ing the Harris detector. Then points at which a lo-

cal measure of variation is maximal over scales are

selected. Finally, an iterative algorithm modiﬁes lo-

cation, scale and local shape of each point and con-

verges to afﬁne invariant points. Scale-space repre-

sentation is also used by (Lowe, 1999) who uses lo-

cal extrema of Difference-of-Gaussian (DoG) ﬁlters

as key-points. Similar ideas are used by other au-

thors (Baumberg, 2000; Schaffalitzky and Zisserman,

2002). For a more detailed review on afﬁne invariant

features detection, please refer to (Mikolajczyk et al.,

2005).

Once the points are detected, the region around

each of them is used to compute a descriptor. In-

variance to afﬁne transformations is provided by the

fact that each point is characterized by a speciﬁc scale

which deﬁnes the size of its region and that each re-

gion has a speciﬁc shape. Many different techniques

for describing local image regions have been devel-

oped and it has been shown that the SIFT (Scale and

Invariant Feature Transform) descriptor performs bet-

Sidibe D., Montesinos P. and Janaqi S. (2007).

FAST AND ROBUST IMAGE MATCHING USING CONTEXTUAL INFORMATION AND RELAXATION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 68-75

 SciTePress

ter than others (Mikolajczyk and Schmid, 2005). This

descriptor is based on the gradient distribution in the

detected regions around the points and is represented

by a 3D histogram of gradient locations and orienta-

tions (Lowe, 1999).

Afﬁne invariant points combined with a distinc-

tive descriptor such as SIFT lead to very good re-

sults in the presence of signiﬁcant transformations.

However, while in the aforementioned works much

effort is done for computing distinctive descriptors,

less attention is paid to the matching strategy. A sim-

ple comparison of the descriptors, for example using

Euclidean or Mahalanobis distance, and matching to

nearest neighbour will always give some mismatches.

This is because no image descriptor is robust enough

to be perfectly discriminant and avoid mismatches.

Thus, an additional step of outliers rejection is often

needed. One approach is to estimate the geometric

transformation between the pair of images and use

this information to reject inconsistent matches (Zhang

et al., 1995). This can, of course, be done only in

stereo-vision or in matching images containing pla-

nar structures for which the epipolar constraint or a

plane homography can be estimated. The accuracy

of the estimation relies on the number of mismatches.

This number can be reduced by considering the ratio

between the ﬁrst and second nearest neighbour, i.e.

matching a point to its nearest neighbour if this one is

much more closer than the second nearest neighbour

(Zhang et al., 1995; Lowe, 1999). Taking into acount

a kind of ambiguity measure, this strategy reduces the

number of mismatches. Unfortunately, it reduces the

number of correct matches as well.

Moreover, when the ambiguity is high as it is in

the presence of repetitive patterns, see Figure 1, the

previous methods fail to ﬁnd correct matches. That is

because, in these cases, all the points have almost the

same SIFT descriptor. So, matching to nearest neigh-

bour gives a lot of mismatches. Taking some addi-

tional information into account during the matching

process could reduce the ambiguity. This is the main

idea of the widely used relaxation labeling technique.

However, most of the existing algorithms (Rosenfeld

et al., 1976; Faugeras and Berthod, 1981) have pro-

hibitive complexity and are therefore limited to the

assignment of a small number of labels.

In this paper, we present a matching method based

on relaxation which can handle large point sets and

provide a very few number of mismatches under im-

portant transformations. This work is based on an al-

gorithm presented by (Faugeras and Berthod, 1981)

and our main contribution is in providing a fast and

efﬁcient implementation of this algorithm. Futher-

more, we show how the contextual information can

be obtained and used in this robust and fast algorithm.

The remainder of the paper is organized as follows.

In Section 2, we decribe the relaxation labeling tech-

niques and show their limits. Then our efﬁcient im-

plementaion is given in Section 3. Experimental re-

sults showing the improvements of the method over

other existing techniques are presented in Section 4.

Finally, concluding remarks are given in Section 5.

Figure 1: A difﬁcult case of matching. Matching to nearest

neighbour fails because of repetitive patterns.

2 RELAXATION MATCHING

2.1 Relaxation Labeling Techniques

The relaxation labeling technique was ﬁrst introduced

by (Rosenfeld et al., 1976) to deal with ambiguity

and noise in vision system. Let u = {u

,...,u

}

and v = {v

,...,v

} be two sets of points from two

images. Each point is characterized by a descrip-

tor. The principal idea of relaxation is to use the

information provided by the neighbourhood of each

point to improve consitency and reduce ambiguity.

More precisely, let deﬁne for each point u

a set of

initial probabilities p

(k),k = 1,...,m; p

(k) being

the probability that point u

is matched with point

. An iterative process is designed to update the

probabilities until a consistent distribution is reached.

The update is based on a support, or compatibility,

function q

deﬁned in the neighbourhood V

the point u

. This support function measures the

likelihood of a point u

to be matched with a point

, given the conﬁguration of its neighbours. Many

probabilistic relaxation schemes have been proposed

and they essentially differ in the deﬁnition of the

support function and the updating rule. For example,

one standard updating rule is deﬁned by (Hummel

and Zucker, 1983) as:

t+1

(k) =

(k)q

(k)

∑

(k)q

(k)

(1)

where

(k) =

∑

(k,l)p

(l)

(2)

and p

(k,l) is the probability that point u

is matched

with point v

under the condition that point u

matched with v

. p

(k,l) is the contextual informa-

tion that helps improving consistency. The scalars w

are weights that indicate the inﬂuence of point u

point u

. They are normalized and verify

∑

= 1.

(Faugeras and Berthod, 1981) propose a relax-

ation scheme based on an optimization approach.

They deﬁne a global criterion to be minimized con-

sidering both consistency and ambiguity:

C = αC

+ (1− α)C

(3)

where the consistency measure is:

∑

i=1

− q

(4)

and the ambiguity measure is:

m− 1

1−

∑

i=1

(5)

Let x be the vector obtained by concatenating the

vectors p

, i.e. x = [p

,..., p

]

. Then, the problem

of ﬁnding a set of corresponding points comes down

to minimizing C(x) subject to the linear constraints:







∑

k=1

(k) = 1 i = 1, . . . , n

(k) ≥ 0 i = 1,...,n k = 1,...,m

(6)

The optimization problem is solved by a projected

gradient method and for each point u

, the point v

with highest ﬁnal probability is retained as its corre-

spondent. This approach seems better since the ﬁnal

set of matches will be more consistent and less am-

biguous. However, it is limited in practice by its high

complexity.

2.2 Drawbacks of the Original Method

The main limitation of the optimization approach

(Faugeras and Berthod, 1981) and the nonlinear

approaches (Rosenfeld et al., 1976; Hummel and

Zucker, 1983) is their high complexity. The former

is in fact a O(nm

V) algorithm where V is the size of

for i = 1,...,n. Thus, these algortihms are appro-

priate to applications such as image segmentation or

classiﬁcation issues where one needs to assign a small

number of labels, i.e. m ≈ O(10

). For applications

such as image matching where one needs to assign a

large number of points from one image to the other,

m ≈ O(10

), the methods become impractical. This

is mainly because the compatibility function q

(see

Equation 2) has to be re-estimated at each iteration.

Another limitation is the fact that the ﬁnal prob-

abilities critically depend on the initial and the con-

ditional probabilities (Hummel and Zucker, 1983;

Price, 1985). If these quantities are not correctly es-

timated, then the ﬁnal probabilities will provide a lot

of mismatches.

In the next section we address these two problems

and we show how the complexity can be considerably

reduced in order to handle large point sets. We also

provide a way of computing the conditional probabil-

ities.

3 FAST AND EFFICIENT

MATCHING ALGORITHM

3.1 Reducing the Complexity

In order to reduce the complexity of the optimization

approach, we show that the criterion C of Equation 3

can be written in the following form:

C(x) =

Hx+ cte (7)

i.e.

C([x

,...,x

]

) =

∑

t=1

∑

p=1

+ cte (8)

where

H =







··· H

. H

··· H







and each matrix H

contains the conditionalprobabil-

ities p

(k,l), i.e. the contextual information needed

to compute the support function q

. See appendix for

details about obtaining the matrices H

Firstly, if we consider in the deﬁnition of the sup-

port function (Equation 2) only points u

which are in

the neighbourhood V

of point u

, then it is clear that

some of the matrices H

are equal to zero. In par-

ticular, it is easy to show that for i = 1,...,n and for

j = 1,...,n:

6= 0 if







i = j or

∈ V

∃k/(u

) ∈ V

×V

(9)

Therefore, using a sparse matrix representation for

H we reduce the complexity of the method. To reduce

the complexity further, we bring down the set of po-

tential matches for each point u

to the set of its K

nearest neighbours given a similarity measure. Thus,

each matrix H

is of size K × K instead of m × m.

With K ≪ m, this reduces memory requirement of the

algorithm.

Secondly, the matrix H is computed only once and

that makes the algorithm faster. At each iteration the

gradient of the criterion is obtained by the following

equation:

∂C

∂x

(H + H

)x (10)

In general, H is not a symmetric matrix. But in the

case it is, the gradient is given by the classical equa-

tion:

∂C

∂x

= Hx (11)

3.2 Initial and Conditional Probabilities

We mentioned already, see Section 2.2, that the re-

sults, i.e. the ﬁnal probabilities, of a relaxation

scheme critically depend on the initial probabilities

and the conditional probabilities. So, estimation of

these quantities is of great interest.

Initial probabilities are computed based on Euclid-

ean distance between descriptors. We used SIFT as it

is considered to be the best local descriptor (Mikola-

jczyk and Schmid, 2005) and we choose the K nearest

neighbours points v

as the potential matches for each

point u

. Then, the initial probabilities are given by

the following equation:

(k) =

1/d

∑

k=1

1/d

i = 1, . . . ,n k = 1,...,K

(12)

where d

is the Euclidean distance between the de-

scriptors of points u

and v

For each interest point u

, the compatibility func-

tion q

indicates how a match assigned to point u

consistent with those of its neighbours in V

. Thus,

can be seen as an estimation of p

given the prior

knowledge represented by the p

(k,l) for points u

in V

. Estimation of the p

(k,l) can be done using

geometric and photometric information of the scene.

Geometric semi-local constraints are used by (Schmid

and Mohr, 1997; Montesinos et al., 2000; Tuytelaars

and Van Gool, 2004). In (Pelillo and Reﬁce, 1994)

the compatibility coefﬁcients are learned from train-

ing examples. We based the estimation of our contex-

tual information on photometric information because

in case of large viewpoint changes, geometry is badly

preserved. Moreover, as the SIFT descriptor gives a

geometric description of a point’s neirghbourhood, it

makes sense to use a complementary photometric in-

formation for matching.

For each point u

and each of its neighbours u

∈

, we deﬁne a rectangular patch M

of length l

and

width l

/2, l

being the distance between u

and u

Note that in order to discard very small patches, we

consider in V

only points u

which are at a distance

from u

greater than 5σ

, σ

being the speciﬁc scale of

point u

∈ V

if d

≥ 5σ

(13)

This is because the detector can ﬁnd two or more

points that are at the same location but with differ-

ent orientations. Each patch is normalized to a unit

square, and conditional probabilities are computed as

normalized cross-correlation between patches in both

images.

3.3 Matching Strategy

In many applications, one-to-one correspondence is

desired. But in general, because of occlusions, vary-

ing background and scale and viewpoint changes, not

all points in u will have a correspondance in v. To

solve this problem, one adds a nil point, v

nil

, to the set

of potential matches of each point u

. Thus, for each

point u

∈ u, the set of potential matches is:

= {v

,...,v

nil

} (14)

where v

,...,v

are the K nearest neighbours points

of u

based on the Euclidean distance between SIFT

descriptors as described in Section 3.2. The matrices

are of size (K + 1) × (K + 1) and can be written

as follows:







(1,1) ··· p

(1,K)

∗∗

(K,1) ··· p

(K,K)

∗∗

··· p

∗∗







(15)

where p

∗∗

is a constant value deﬁning the conditional

probabilities for v

nil

. Initial probabilities for v

nil

are

also set to a constant value:

nil

) = p

∗

i = 1,...,n (16)

Once the matrices H

are obtained, the matrix H

is computed (see Section 3.1) and the optimization

problem is solved by a projected gradient method.

The algorithm converges to a local minimum after a

reduced number of iterations and for each point u

the potential match with highest ﬁnal probability is

retained as its correspondent. Points in one image

which have no correspondent in the other image are

expected to match with v

nil

Figure 2: Examples of images used for wide baseline matching. Top: ﬁrst, third and ﬁfth frame of the Graf. sequence.

Bottom: ﬁrst, third and ﬁfth frame of the Boat sequence.

4 EXPERIMENTAL RESULTS

In this section we report some experimentscarried out

on real images to evaluate the performance of the al-

gorithm. First, we have conducted experiments in the

case of matching with large baseline using some im-

ages from (Mikolajczyk and Schmid, 2005)

and the

images presented in Figure 1. Secondly, we apply the

method to features-based object recognition. In all

our experiments we set V = K = 5, i.e. each point

has 5 neighbours and 5 potential matches. We set

the constant α of the criterion C (Equation 3) to 0.5,

i.e. consistency and ambiguity measures are given the

same importance. And initial and conditional prob-

abilities for the nil point are taken equal to 0.1, i.e.

∗

= p

∗∗

= 0.1.

We compare our method, named ORELAX for op-

timization approach, with the three following tech-

niques:

• CRELAX: relaxation technique using the classi-

cal updating rule deﬁned in Equation 1 (Hummel

and Zucker, 1983);

• NNDR: nearest neighbour distance ratio (Lowe,

1999). That is a point is matched to its nearest

neighbour if this one is much more closer than the

second nearest neighbour:

= min(D

) < 0.6min(D

− {d

})

where D

= {d

,l = 1,... ,m};

• SVD: a SVD-based method using SIFT features

(Delponte et al., 2006). A proximity matrix G is

computed using SIFT descriptors of points, and

matches are found based on a SVD decomposition

of G:

= e

−d

/2σ

Images are available at

http://www.robots.ox.ac.

uk/

vgg/research/affine/

4.1 Wide Baseline Matching

For these experiments the homographies between dif-

ferents views are available and we can compute the

matching rate (MR) of a matching method as the ratio

between the number of correct matches and the num-

ber of detected matches.

MR =

# o f correct matches

# o f detected matches

(17)

A couple of corresponding points (p, p

′

) is said to be

a correct match if:

′

− H pk < 5 (18)

where H is the homography between the two images.

We use two sequences, the Graf and the Boat se-

quences for evaluation. The former is a six frames

sequence with important viewpoint change between

the ﬁrst and the following frames, and the later is a

six frames sequence with rotation and scale change.

Some of these images are shown in Figure 2.

We present an example of matching results ob-

tained by our method for the Graf sequence in Fig-

ure 3. There are respectively 1401 and 1279 interest

points detected in the ﬁrst and fourth frames. The al-

gorithm ﬁnds 82 matches between these two frames

and 71 of them are correct.

Figure 3: Example of matching results with the Graf. se-

quence: 71 corrects matches are found between the ﬁrst and

fourth frames.

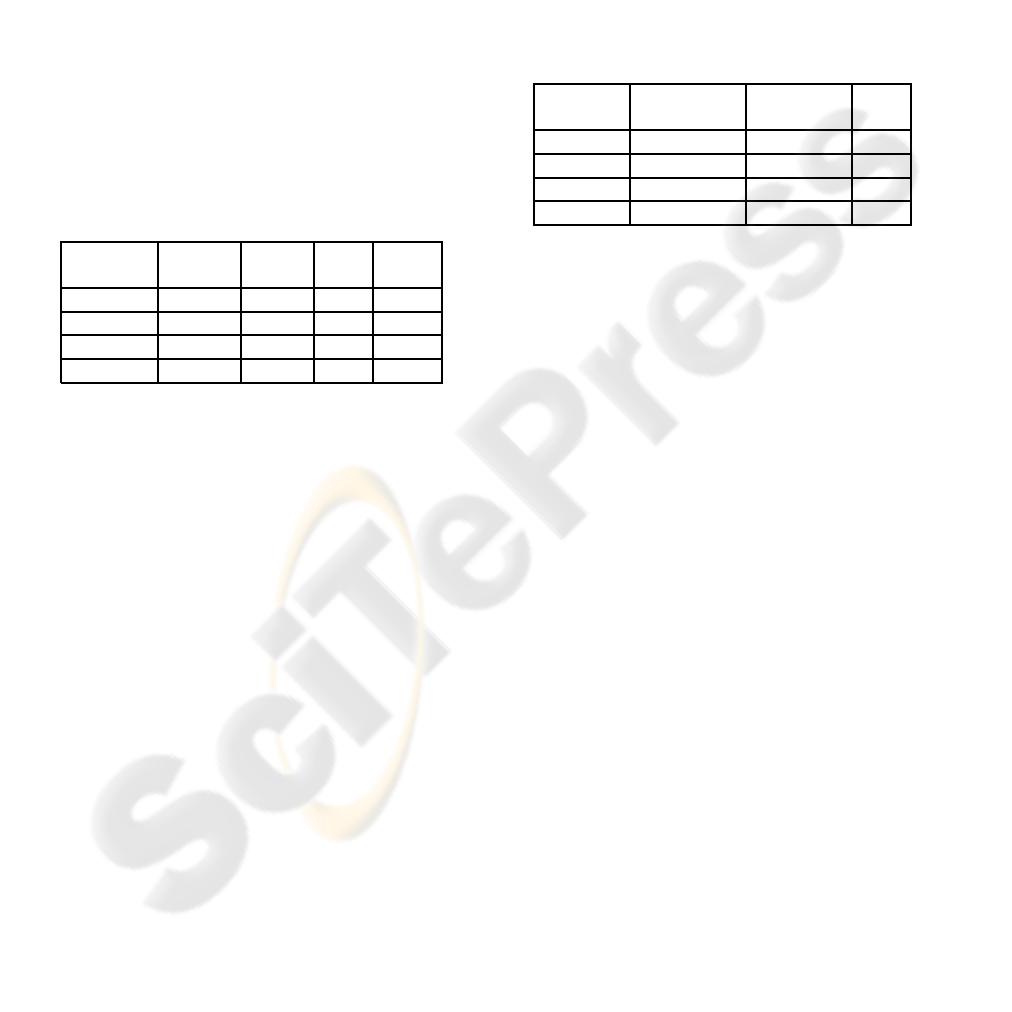
Table 1 shows comparative results obtained with

the different methods. It can be seen that for this difﬁ-

cult case, ORELAX gives considerably more matches

than NNDR while maintining a high MR (matching

rate). SVD and CRELAX also provide a large num-

ber of matches but with a very poor MR, less than

0.5. This is mainly because the SVD decomposition

algorithm has stability problems when dealing with

large matrices. We used the algorithm implemented

in MATLAB for our experiments. Therefore, instead

of improving results, SVD based method spoils the

results obtained by simple descriptors comparison as

with NNDR. Moreover, ORELAX is much faster than

SVD. It is slower than NNDR since the later sim-

ply compares Euclidean distance between descriptors.

ORELAX is faster than CRELAX because of the op-

timization step which lead to a fewer number of iter-

ations for the former.

Table 1: Comparison of different algorithms using the ﬁrst

and fourth frames of the Graf. sequence.

Methods # of # of MR time

matches correct in s

ORELAX 82 71 0.86 8.56

NNDR 35 26 0.74 2.9

SVD 118 58 0.49 47.1

CRELAX 84 34 0.40 11.41

Additional results for the whole Graf sequence

are shown in Table 3. We see that the relaxation

method with optimization gives better results for

varying viewpoints. ORELAX returns the highest

number of matches with the highest MR. NNDR gives

the second best performance but it returns about twice

less matches than ORELAX. SVD and CRELAX

have poor MR for the last three frames. The num-

ber of matches goes down sensibly when viewpoint

change becomes important. For example, viewpoint

change between the ﬁrst and ﬁfth frames of the Graf

sequence is greater than 50 degres. The SIFT descrip-

tor cannot cope with such large viewpoint as reported

in (Mikolajczyk and Schmid, 2005; Delponte et al.,

2006).

Results obtained for the Boat sequence are pre-

sented in Table 4. They are similar to those obtained

with the Graf sequence but there are more correct

matches for the last frames. Moreover, the MR of

ORELAX and NNDR is almost always equal to 1 ex-

cept for the last frame. This means that the SIFT de-

scriptor is more suited to rotation and scale changes

than to large viewpoint changes.

In the case of repetitive patterns as in Figure 1,

the relaxation method with optimization gives better

results. Results presented in Table 2 show that a sim-

ple comparison of descriptor fails to ﬁnd enough cor-

rect matches. The number of matches provided by

NNDR is too small and the the proportion of outliers

obtained by SVD is too high. Therefore, an estima-

tion of the geometric transformationby a method such

as RANSAC will fail. On the contrary, ORELAX

gives almost six times more matches than NNDR with

a high MR. It is important to emphasize that in this

difﬁcult case, one should consider a high number of

potential matches for each point to reduce ambiguity.

We set K = 7. See Section 4.3 for a discussion about

the inﬂuence of algorithm’s parameters.

Table 2: Comparison of different algorithms using the im-

ages in Figure 1.

Methods # of matches # of correct MR

matches

ORELAX 38 25 0.66

NNDR 6 3 0.50

SVD 60 21 0.35

CRELAX 120 26 0.22

4.2 Object Recognition

We also compare the different algorithms in a case

of features-based object recognition. The results are

shown in Figure 4. For the ﬁrst experiment, a book is

placed on a desktop such that it is partially occluded

and has its scale, orientation and viewpoint changed.

There are respectively 193 and 2541 interest points

detected on the object, shown in the top of Figure 4a,

and on the entire scene shown in the bottom of Fig-

ure 4a. ORELAX ﬁnds 20 matches, all of which are

corrects, while NNDR ﬁnds only 7. CRELAX ﬁnds

8 correct matches and SVD gives 12 correct matches

over 18 detected matches.

For the more difﬁcult case shown in Figure 4b,

ORELAX ﬁnds 5 correct matches over 8 detected

matches, while the other methods fail to ﬁnd any cor-

rect matches. Note that the images are shown at their

actual relative scale.

4.3 Inﬂuence of Algorithm’s Parameters

Results depend on the values of the algorithm’s pa-

rameters. It is clear that the greater V and K are,

the more accurate the method will be at the cost of

a longer processing time.

To measure the inﬂuence of the parameter α, we

use the same pair of images. The results presented in

Table 5 show that if more importance is given to the

consistency term of the criterion, i.e. α > 0.5, then

the MR of the method increases but the number of

matches decreases. On the contrary, if more impor-

tance is given to the ambiguity term, i.e. α < 0.5,

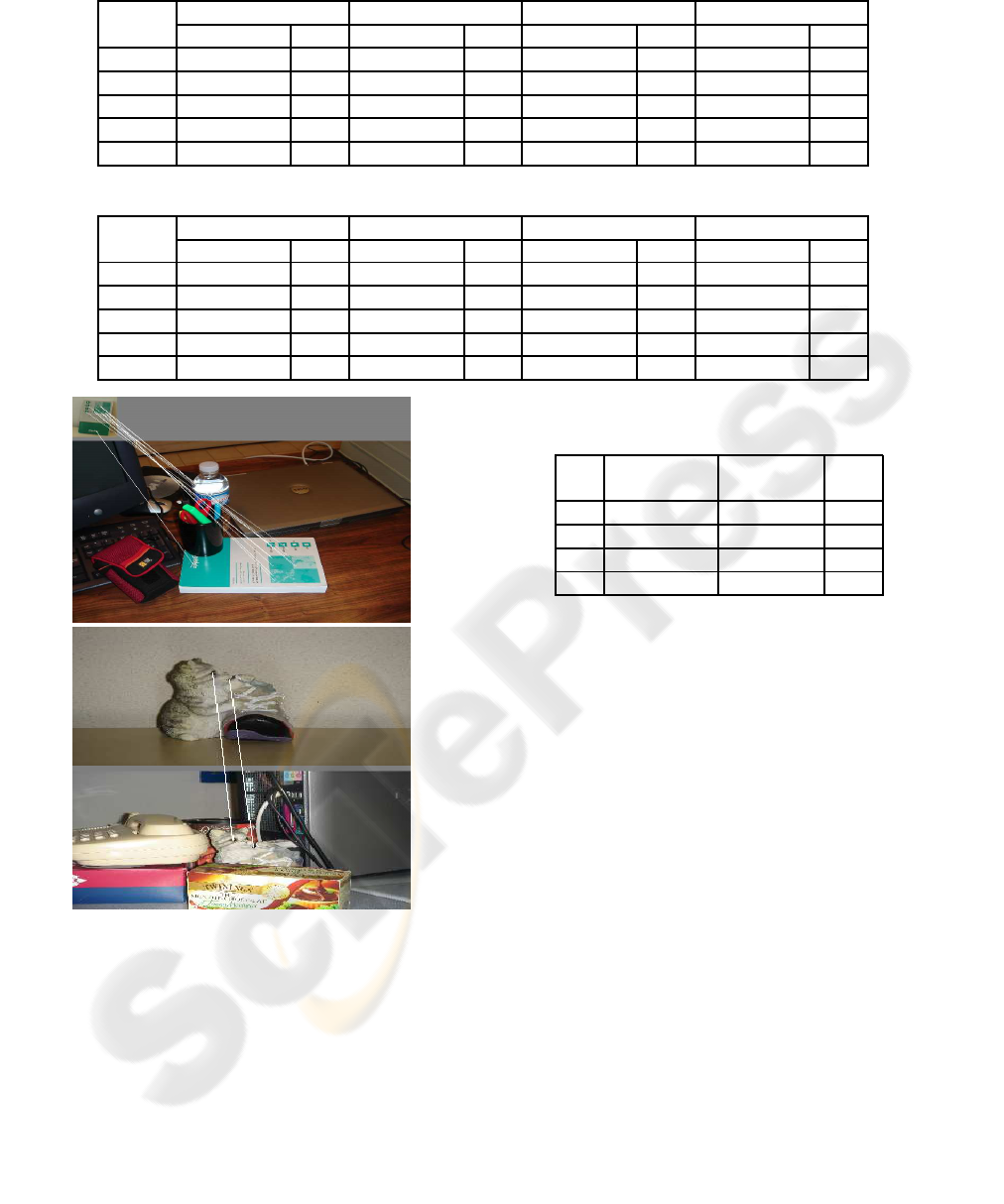
Table 3: Comparison of different algorithms using the Graf. sequence.

Frame ORELAX NNDR SVD CRELAX

number # of matches MR # of matches MR # of matches MR # of matches MR

2 530 0.98 261 0.97 363 0.89 384 0.94

3 180 0.93 91 0.70 222 0.67 198 0.58

4 82 0.86 35 0.74 118 0.49 84 0.40

5 11 0.72 3 0.67 60 0.13 35 0.03

6 5 0.6 9 0 40 0.1 27 0

Table 4: Comparison of different algorithms using the Boat. sequence.

Frame ORELAX NNDR SVD CRELAX

number # of matches MR # of matches MR # of matches MR # of matches MR

2 620 0.99 294 0.98 427 0.91 490 0.93

3 488 0.99 183 0.99 365 0.87 289 0.94

4 127 0.99 58 0.99 125 0.84 97 0.45

5 75 0.99 46 0.99 76 0.83 79 0.3

6 8 0.75 6 0.5 47 0.45 46 0.08

Figure 4: Examples of recognition results. a): ORELAX

ﬁnds 20 matches all of which are correct. b): ORELAX

ﬁnds 8 matches and 5 of them are correct.

then the number of matches increases while the MR

of the method decreases.

There is a balance to ﬁnd between the matching

rate and the number of detected matches. We have

found that the values V = k = 5 (K = 7 in the case

of repetitive patterns) were sufﬁcient for our experi-

ments. The results presented in the previous sections

are obtained with α = 0.5, i.e. consistency and ambi-

guity measures are given the same importance.

Table 5: Inﬂuence of the parameter α using the images of

Figure 1.

α # of matches # of correct MR

matches

0.3 88 42 0.48

0.5 38 25 0.66

0.7 23 17 0.74

0.9 15 13 0.87

5 CONCLUSION

In this paper a fast and robust image matching method

is proposed. The method is based on relaxation la-

beling technique and optimization. We showed that

writing the criterion to mimize in a convenient way

and using a distinctive descriptor such as SIFT, the

complexity of the algorithm can be considerably re-

duced. Futhermore, we showed how the necessary

contextual information can be obtained in order to im-

prove matching results and reduce the number of mis-

matches. Experimental results in case of wide base-

line and in case of object recognition show that this

approach gives superior results compared with other

matching methods. Roughly speaking, we gain at

least 30% on the number of matches and the number

of correct matches as well. We obtain, in most experi-

ments we have done, a very small error rate which al-

low us to avoid an additional step of outliers rejection

by estimating the geometric transformation between

the pair of images.

In the future we are going to investigate the use of

several image features into a single matching process

and the matching of non-rigid objects and non-planar

scenes.

REFERENCES

Baumberg, A. (2000). Reliable feature matching across

widely separated views. In Proc. Conf. Computer Vi-

sion and Pattern Recognition, pages 774–781.

Delponte, E., Isgro, F., Odone, F., and Verri, A. (2006).

Svd-matching using sift features. Graphical Models,

68:415–431.

Faugeras, O. D. and Berthod, M. (1981). Improving consis-

tency and reducing ambiguity in stochastic labeling:

An optimization approach. IEEE PAMI, 3(4):412–

424.

Hummel, R. A. and Zucker, S. W. (1983). On the funda-

tions of relaxation labeling processes. IEEE PAMI,

5(3):267–287.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In International Conference on

Computer Vision, pages 1150–1157. Corfu, Greece.

Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002). Ro-

bust wide baseline stereo from maximally stable ex-

tremal regions. In Proc. 13th British Machine Vision

Conference, pages 384–393.

Mikolajczyk, K. and Schmid, C. (2002). An afﬁne invariant

interest point detector. In European Conference on

Computer Vision (ECCV’2002). Copenhag, Denmark.

Mikolajczyk, K. and Schmid, C. (2004). Sacle & afﬁne

invariant interest point detectors. Internationl Journal

of Computer Vision, 60(1):63–86.

Mikolajczyk, K. and Schmid, C. (2005). A performance

evaluation of local descriptors. IEEE Trans on PAMI,

27(10):1615–1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L. V.

(2005). A comparison of afﬁne region detectors. Inter-

nationl Journal of Computer Vision, 65(1/2):43–72.

Montesinos, P., Gouet, V., Deriche, R., and Pele, D. (2000).

Matching color uncalibrated images using differential

invariants. Image and Vision Computing, 18:659–671.

Pelillo, M. and Reﬁce, M. (1994). Learning compatibility

coefﬁcients for relaxation labeling processes. IEEE

PAMI, 16:933–945.

Price, K. E. (1985). Relaxation matching techniques - a

comparison. IEEE PAMI, 7(5):617–623.

Rosenfeld, A., Hummel, R., and Zucker, S. (1976). Scene

labeling by relaxation operations. IEEE Trans. Sys-

tems. Man Cybernetics, 6:420–433.

Schaffalitzky, F. and Zisserman, A. (2002). Multi-view

matching for unordered image sets. In Proc. 7th Euro-

pean Conference on Computer Vision, pages 414–431.

Schmid, C. and Mohr, R. (1997). Local grayvalue invariants

for image retrieval. PAMI, 19(5):530–534.

Tuytelaars, T. and Van Gool, L. (2004). Matching widely

separated views based on afﬁne invariant regions. In-

ternational Journal of Computer Vision, 59(1):61–85.

Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.

(1995). A robust technique for matching two uncal-

ibrated images through the recovery of the unknown

epipolar geometry. AI Journal, 78:87–119.

APPENDIX

Re-writing the Criterion with Matrices

The criterion to be minimized can be written:

C(x) = αC

(x) + (1−α)C

(x)

∑

i=1

− q

(1− α)m

m− 1

1−

∑

i=1

= c

∑

i=1

− q

− c

∑

i=1

+ c

with c

, c

(1−α)m

(m−1)n

and c

= nc

One wants to put C on the form:

C([x

,..., x

]

) =

∑

t=1

∑

p=1

+ cte

Let remark that the constant is equal to c

. So one has:

C(x) =

∑

i=1

− q

− c

) + c

∑

i=1

− q

)

− q

) − c

) + c

= (c

− c

)

∑

i=1

{z }

−2c

∑

i=1

{z }

∑

i=1

{z }

The criterion is the weighetd sum of three terms which one

notes respectively A, B and C. Let deﬁne the following two

symbols:



1 if t = p

0 otherwise



1 if a

∈ V

0 otherwise

Then, it is easy to show that:

A =

∑

t=1

∑

p=1

where ∀ t, p ∈ {1. ..n}, A

= δ

B =

∑

t=1

∑

p=1

where ∀ t, p ∈ {1,.. . ,n}, B

and P

is the

matrix of size m× m containning the conditional probabili-

ties p

(k,l), and |V

| = #{V

C =

∑

t=1

∑

p=1

where ∀ t, p ∈ {1,. .. ,n}, C

∑

i=1

)

Finally,

C([x

,. .., x

]

) =

∑

t=1

∑

p=1

+ c

with

∀ t, p∈ {1,... ,n}, H

= 2(c

−c

−4c

+2c