ESTIMATING LARGE LOCAL MOTION IN LIVE-CELL IMAGING

USING VARIATIONAL OPTICAL FLOW

Towards Motion Tracking in Live Cell Imaging Using Optical Flow

Jan Huben

y, Vladim

ır Ulman and Pavel Matula

Centre for Biomedical Image Analysis, Faculty of Informatics Masaryk University, Botanick

a 68a, Brno 602 00, Czech Republic

Keywords:

Live-cell imaging, motion tracking, 3D imaging, variational optical ﬂow.

Abstract:

The paper studies the application of state-of-the-art variational optical ﬂow methods for motion tracking of

ﬂuorescently labeled targets in living cells. Four variants of variational optical ﬂow methods suitable for

this task are brieﬂy described and evaluated in terms of the average angular error. Artiﬁcial ground-truth

image sequences were generated for the purpose of this evaluation. The aim was to compare the ability of

those methods to estimate local divergent motion and their suitability for data with combined global and local

motion. Parametric studies were performed in order to ﬁnd the most suitable parameter adjustment. It is shown

that a selected optimally tuned method tested on real 3D input data produced satisfactory results. Finally, it is

shown that by using appropriate numerical solution, reasonable computational times can be achieved even for

3D image sequences.

1 INTRODUCTION

There is a steadily growing interest in live cell stud-

ies in modern cell biology. The progress in staining

of living cells together with advances in confocal mi-

croscopy devices has allowed detailed studies of the

behaviour of intracellular components including the

structures inside the cell nucleus. The typical num-

ber of investigated cells in one study varies from tens

to hundreds because of statistical signiﬁcance of the

results. One gets time-lapse series of three or two di-

mensional images as an output from the microscope.

It is very inconvenient and annoying to analyze such

data sets by hand (especially for 3D series). More-

over, there is no guarantee on the accuracy of the re-

sults. Therefore, there is a natural demand for com-

puter vision methods which can help with analysis of

these time-lapse image series. Estimation or correc-

tion of global as well as local motion belongs to main

tasks in this ﬁeld. The suitability of the state-of-the-

art optical ﬂow methods for correction of local motion

will be studied in this article.

The live-cell studies are mainly performed using

the confocal microscopes these days. The confocal

microscopes are able to focus on selected z-plane of

the specimen in the same way as the standard wide-

ﬁeld (non-confocal) microscopes. However, they are

based on principle of suppression of light from planes

which are out of focus. Therefore, they provide far

better 3D image data (less blurred) than wide-ﬁeld

microscopes. The main disadvantage of confocal mi-

croscopes is their lower light throughput. This causes

larger exposure times as compared to the wide-ﬁeld

mode. Several optical setups suitable for live-cell

imaging as well as their optimization and automation

are discussed in detail in (Kozubek et al., 2004).

Transparent biological material is visualized with

ﬂuorescent proteins in live-cell imaging. Living spec-

imen usually does not contain ﬂuorescent proteins.

Therefore, the living cells are forced to produce those

proteins in the specimen preparation phase (Chalﬁe

et al., 1994). The image of the living cells in the

specimen on the microscope stage is acquired peri-

odically. The cells can move or change their internal

structure in the meantime. The interval between two

consecutive acquisitions varies in range from frac-

tions of second up to tens of minutes. It would be

convenient to acquire snapshots frequently in order

to have only small changes between two consecutive

frames. But, the interval length cannot be arbitrary

542

Hubený J., Ulman V. and Matula P. (2007).

ESTIMATING LARGE LOCAL MOTION IN LIVE-CELL IMAGING USING VARIATIONAL OPTICAL FLOW - Towards Motion Tracking in Live Cell Imaging

Using Optical Flow.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 542-548

 SciTePress

small mainly because of photo-toxicity (the living

specimen is harmed by the light) and photo-bleaching

(the intensity of ﬂuorescent markers fades while be-

ing exposed to the light). However, it is usually pos-

sible to ﬁnd a reasonable compromise between those

restrictions and adjust the image acquisition so that

the displacement of objects between two consecutive

snapshots is not more than ten pixels.

There are two types of tasks to be solved in this

ﬁeld. First, the global movement of objects should

be corrected before subsequent analysis of an intra-

cellular movement. This goal is often achieved us-

ing common rigid registration methods (Zitov

a and

Flusser, 2003). A fast 3D point based registration

method (Matula et al., 2006) was recently proposed

for the global alignment of cells.

The second task is to estimate local changes in-

side the objects. This task is more complex. The ob-

jects inside the cells or nuclei can move in different

directions. One object can split into two or more ob-

jects and vice versa. Moreover, an object can appear

or disappear during the experiment. Therefore, this

task requires computation of dense motion ﬁeld be-

tween two consecutive snapshots. Manders et. al. has

used block-matching (BM3D) algorithm (de Leeuw

and van Liere, 2002) for this purpose in their study

of chromatin dynamics during the assembly of inter-

phase nuclei (Manders et al., 2003). Their BM3D

algorithm is rather slow. It is similar to basic optic

ﬂow methods but it does not comprise any smooth-

ness term.

We study latest optical ﬂow methods (Bruhn,

2006) for estimation of intracellular movement in this

paper. Up to our best knowledge, nobody investi-

gated the application of these state-of-the-art meth-

ods in live-cell imaging. The simple ancestors of

these methods, which can reliably estimate one pixel

motion, were successfully used for lung motion cor-

rection (Dawood et al., 2005). The examined meth-

ods are able to reliably estimate the ﬂow larger than

one pixel. They can produce piece-wise smooth ﬂow

ﬁelds which preserve the discontinuities in the ﬂow

on object boundaries. These properties are needed for

estimation of local divergent motion which occur in

live-cell imaging. We have extended state-of-the-art

optical ﬂow methods into three dimensions. Espe-

cially, we focused on 3D extension of recently pub-

lished optical ﬂow methods for large displacements

(Papenberg et al., 2006). We tested these methods on

synthetic as well as real data and compared their be-

haviour and performance. Our experiments identify

the optical ﬂow methods which can be used in live cell

imaging. We used the efﬁcient numeric techniques for

the optical ﬂow computations (Bruhn, 2006). This al-

lows us to get reasonable computational times even

for 3D image sequences.

The rest of the paper is organized as follows: The

variational optical ﬂow methods are described in Sec-

tion 2. Section 3 is devoted to the experiments and re-

sults obtained for synthetic and real biomedical data.

2 OPTICAL FLOW

In this section, we describe the basic ideas of varia-

tional optical ﬂow methods and in particular the meth-

ods which will be tested in Section 3.

Let two consecutive frames of image sequence be

given. Optical ﬂow methods compute the displace-

ment vector ﬁeld which maps all voxels from ﬁrst

frame to their new position in the second frame. Al-

though several kinds of strategies exist for optical

ﬂow computation (Barron et al., 1994), we take only

the so-called variational optical ﬂow (VOF) methods

into our considerations. They currently give the best

results (in terms of error measures) (Papenberg et al.,

2006; Bruhn and Weickert, 2005) and come out from

transparent mathematical modeling (the ﬂow ﬁeld is

described by energy functional). Furthermore, they

produce dense ﬂow ﬁelds and are invariant under ro-

tations.

The ﬁrst prototype of VOF method was proposed

in (Horn and Schunck, 1981). Horn and Schunck

used the grey value constancy assumption which as-

sumes that the grey value intensity of the moving ob-

jects remains the same and homogenous regulariza-

tion which assumes that the ﬂow is smooth. We will

describe their method ﬁrst, because even the most so-

phisticated methods available are based on the funda-

mental ideas of Horn and Schunck method.

Let Ω

⊂ R

denote the 4-dimensional spatial-

temporal image domain and f(x

, . . . , x

) : Ω

→ R

a gray-scale image sequence, where (x

, x

)

⊤

is a

voxel location within a image domain Ω

⊂ R

and

∈ [0, T] denotes the time. Moreover, let’s assume

that ∆x

= 1 and u = (u

, u

, 1)

⊤

denotes the un-

known ﬂow. The grey value constancy assumption

says

f(x

, . . . , x

, x

+1)− f(x

, . . . , x

) = 0 (1)

Optic ﬂow constraint (OFC) is obtained by approxi-

mation of (1) with ﬁrst-order Taylor expansion

+ f

= 0, (2)

where f

is partial derivative of f. Equation (2) with

three unknowns has obviously more than one solu-

tion. Horn and Schunck assumed only smooth ﬂows

and they therefore penalized the solutions which have

large spatial gradient ∇

where i ∈ 1, 2, 3 and ∇

de-

notes the spatial gradient. Thus, the sum

∑

i=1

|∇

for every voxel should be as small as possible. We

get following variational formulation of the problem

if we combine these two considerations together:

(u) =

Ω

( f

+ f

)

+ α

∑

i=1

|∇

(3)

The optimal displacement vector ﬁeld minimizes en-

ergy functional (3). The OFC and the regularizer are

squared, the α parameter has the inﬂuence on the

smoothness of the solution. The two terms which

form the functional are called data and smoothness

term. Following the calculus of variations (Gelfand

and Fomin, 2000), the minimizer of (3) is a solution

of Euler-Lagrange equations

0 = f

+ f

+ αdiv(∇

)

0 = f

+ f

+ αdiv(∇

)

0 = f

+ f

+ αdiv(∇

)

(4)

with reﬂecting Neumann boundary conditions. div(x)

is the divergence operator. The system (4) is usu-

ally solved with common numerical methods like

Gauss-Seidel or SOR. The bidirectional full multigrid

(Briggs et al., 2000) framework for computations of

VOF methods was proposed in (Bruhn et al., 2005).

The computations with multigrid methods are by or-

ders of magnitude faster than the classic Gauss-Seidel

or SOR methods.

Now we describe the VOF methods which will be

tested in Section 3. The current state-of-the-art VOF

methods are still similar to their Horn-Schunck pre-

cursor. Their energy functional consists of data and

smoothness term. The combined local-global (CLG)

method for large displacements proposed in (Papen-

berg et al., 2006) is the ﬁrst method which we have

tested. This method produces one among the most

accurate results (Bruhn, 2006). We assume that it will

be suitable for our data, because it produces smooth

ﬂow ﬁelds and simultaneously ﬂow ﬁelds with dis-

continuities. The energy functional of CLG method

is deﬁned as:

CLG

(u) =

Ω

(| f(x+ u) − f(x)|

)

+ αΨ

∑

i=1

|∇

(5)

where

(s) =

+ ε

(s) =

+ ε

and ε

, ε

are reasonably small numbers (e.g. ε

0.01). Note that the data term consists of non-

linearized grey value constancy assumption (1). This

allows to correct estimate of the large displacements.

Moreover, the CLG method uses the non-quadratic

penalizers Ψ

(s) and Ψ

(s) and therefore it is ro-

bust with respect to noise and outliers. Nevertheless,

these concepts make the minimization of (5) quite

complex. We use the multi-scale warping based ap-

proach, which proposed in (Papenberg et al., 2006),

for minimization of (5). The multigrid numerical

framework for this task was extensively analyzed in

(Bruhn, 2006; Bruhn and Weickert, 2005).

The second tested method consists of robust data

term and anisotropic image driven smoothness term

(Nagel and Enkelmann, 1986). We denote this

method RDIA. Its energy functional is deﬁned:

RDIA

(u) =

Ω

(| f(x+ u) − f(x)|

)

+ α

∑

i=1

(∇

⊤

(∇

f)∇

) dx

(6)

where P

(∇

f) is projection matrix perpendicular to

∇

f deﬁned as

2|∇

+ 3ε





a b c

b d e

c e f





(7)

where

a = f

+ f

+ ε

d = f

+ f

+ ε

b = − f

e = − f

c = − f

f = f

+ f

+ ε

The ε is reasonably small number (e.g. ε = 0.01).

The only difference between CLG and RDIA method

is the smoothing term. RDIA method smoothes the

ﬂow with respect to underlying image. The image

data in live-cell imaging are often low contrast due

to the limitations of the optical setup. We assume that

this smoothing term can help with processing of such

data. The same minimization approach can be used as

for the CLG method.

The third and fourth tested method are variants of

the previous two. We add the gradient constancy as-

sumption to the data term. This should provide us bet-

ter results on image sequences which fade out with in-

creasing time. The energy functional of CLG method

with gradient constancy assumption is deﬁned as

CLG

(u) =

Ω

(| f(x+ u) − f(x)|

+ γ(|∇ f (x+ u) − ∇ f (x)|

))

+ αΨ

∑

i=1

|∇

(8)

The variant of RDIA method with gradient constancy

assumption is deﬁned as

RDIA

(u) =

Ω

(| f(x+ u) − f(x)|

+ γ(|∇ f (x+ u) − ∇ f (x)|

))

+ α

∑

i=1

(∇

⊤

(∇

f)∇

) dx

(9)

where γ is the parameter which controls the inﬂuence

of gradient constancy assumption. Note that the gra-

dient constancy assumption is again included in the

non-linearized form.

3 RESULTS AND DISCUSSION

In this section, we test the behaviour of CLG, RDIA,

CLG

and RDIA

methods on artiﬁcial and real im-

age data. We measure their performance on live-

cell image sequences with large local displacements.

Moreover, we present the results of the methods on

image sequences with combined global rigid (trans-

lation, rotation) and local displacements. We present

the results on both two and three dimensional data.

Finally, we discuss the computational time and stor-

age demands.

The ground-truth ﬂow ﬁelds are needed for the

evaluation purposes. Obviously, they are not avail-

able for real image sequences. Therefore, we gener-

ate the artiﬁcial data with artiﬁcial ﬂow ﬁelds from

the real image data. We use the two-layered approach

in which user-selected foreground is locally moved

and inserted into an artiﬁcially generated background.

Hence, our generator requires one real input frame,

the mask of the cell (the background) and the mask

of the objects (the foreground). Both ﬁrst and sec-

ond frames are generated in two steps. First, the

foreground objects are extracted, an artiﬁcial back-

ground is generated and the rigid motion is applied

on background and foreground separately. Second,

every foreground object is translated independently

on each other and ﬁnally inserted into the generated

background. The movements were performed by us-

ing backward registration technique (Lin and Barron,

Figure 1: Generation of artiﬁcial data. We use two-layered

approach. Both artiﬁcial frames are generated from the real

input frame. The second frame is almost identical to the real

one. The ﬁrst frame is the backward registered copy of sec-

ond frame. The artiﬁcial ground-truth ﬂow ﬁeld is used for

the backward registration. The background and foreground

movements are independent. (top left). Real input frame.

(top right) Cell nucleus mask (background) in white, object

mask (foreground) in red. (bottom left) Second artiﬁcial

frame. (bottom right) First artiﬁcial frame (red channel)

superimposed over second frame (green channel).

1994) according to the generated ﬂow ﬁeld. This ﬂow

determines the movement and becomes the ground-

truth ﬂow. The ﬂow ﬁeld determines the movement

uniquely. Thus, it becomes the ground-truth ﬂow ﬁeld

between these two frames and can be used for testing

purposes. Owing to the property of the backward reg-

istration technique, the ﬁrst frame represents the in-

put real image before the movement while the second

frame represents it after the movement. Therefore, the

second frame is similar to the real input image. The

generation process is illustrated in Fig. 1.

The ﬁrst experiment was performed on artiﬁcial

two dimensional data. We prepared a data set of arti-

ﬁcial images with large local displacements. The data

set consisted of six different frame couples. The size

of input frames was 400× 400 pixels. The number of

objects which moved inside the nucleus varies from

seven to eleven. The size of the individual translations

vectors varies from 1.2 to 11.3 pixels. According to

the literature, the input frames were ﬁltered with gaus-

sian blur ﬁlter with standard deviation σ = 1.5. We

performed a parametric study over α parameter for

four tested methods over whole data set. The results

were compared with respect to average angular error

(AAE) (Fleet and Jepson, 1990) where angular error

is deﬁned as

arccos





)

+ (u

)

+ 1

((u

)

+ (u

)

+ 1)((u

)

+ (u

)

+ 1)





(10)

where (u

)

, (u

)

denote the i-component of ground-

truth and estimated vector, respectively. There were

two coupled goals behind this experiment. We wanted

to identify the best method by the mean of AAE and

at the same time ﬁnd suitable setting of α parameter.

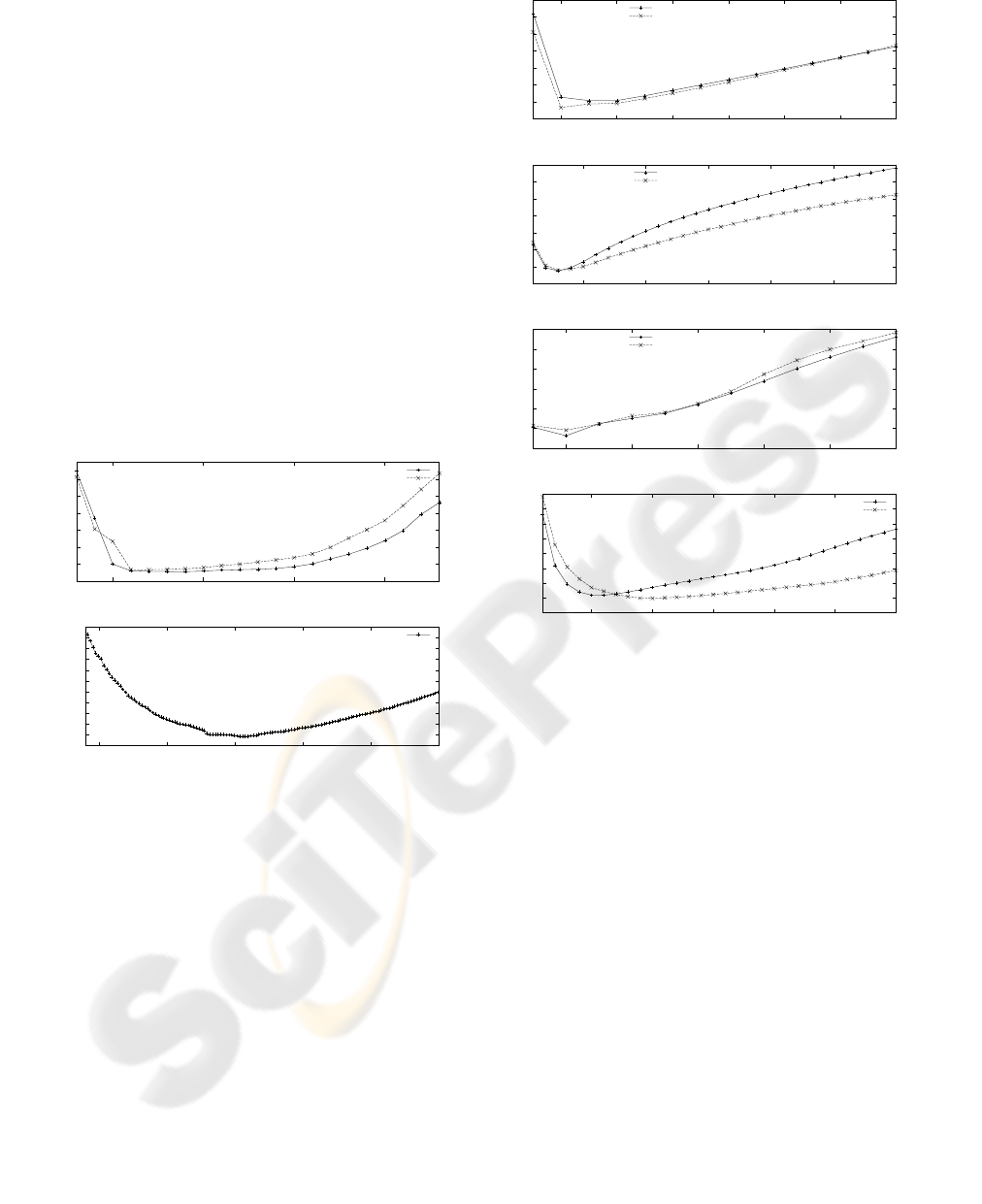
The results are presented in Fig. 2. The AAE was

computed for each run of particular method with par-

ticular α. Then, the averages of AAE over the frame

pairs in the data set were computed. These averages

are depicted in the graphs in Fig. 2. The AAE was

computed only inside the moving objects. We can see

that all methods perform reasonably well. The CLG

method is outperformed by the RDIA method. The

gradient variant of CLG provided better results than

the simple CLG method. The RDIA

method is not

depicted in the graph because we noticed that its re-

sults depended on data and the average value was bi-

ased. It was slightly better than simple RDIA method

in some cases. But, it was slightly worse in other

cases.

5 10 15 20

AAE

α parameter

AAE of CLGg method

AAE of CLG method

2.16

2.18

2.2

2.22

2.24

2.26

2.28

2.3

2.32

2.34

2.36

2.38

50 100 150 200 250 300

AAE

α parameter

AAE of RDIA method

Figure 2: The dependency of average angular error on α pa-

rameter. The methods were tested on artiﬁcial image data

with large local displacements up to 11.3 pixels. (top).

CLG and CLG

method. (bottom) RDIA method.

The goal of the second experiment was to examine

the performance of the tested methods on sequences

with combination of global and local movement. We

again prepared a dataset with artiﬁcial frame pairs.

Image size and other input sequence properties were

the same as in the previous experiment. The cell nu-

clei were transformed with global translation (up to

5 pixels) and rotation (up to 4 degrees). After that

the local displacement were applied on the foreground

object inside. It becomes clear from our experiments

that we should divide the data into two groups. The

results of the computations were inﬂuenced by the

following fact. If the majority of objects inside the

cell nucleus moved in the direction similar to the

2 4 6 8 10 12 14

AAE

α parameter

AAE of CLGg method

AAE of CLG method

50 100 150 200 250 300

AAE

α parameter

AAE of RDIAg method

AAE of RDIA method

4 6 8 10 12 14

AAE

α parameter

AAE of CLGg method

AAE of CLG method

8.5

9.5

10.5

11.5

12.5

50 100 150 200 250 300

AAE

α parameter

AAE of RDIAg method

AAE of RDIA method

Figure 3: The dependency of average angular error on α

parameter. The methods were tested on artiﬁcial image

data with global movement (translation up to 5 pixels, ro-

tation up to 4 degrees) and large local displacements up to

11.3 pixels. (top). CLG and CLG

method. (upper cen-

ter) RDIA and RDIA

method. Majority of local displace-

ments have the same direction as compared to global move-

ment (top, upper center). (lower center) CLG and CLG

method. (bottom) RDIA and RDIA

method. Majority

of local displacements has different direction than global

movement (lower center, bottom).

global translation the results fell into the ﬁrst group

and vice versa. The AAE was computed on the cell

nucleus mask (see the Fig. 1) in this experiment. The

results for both groups are illustrated in Fig. 3.

We tested the methods with best parameter set-

tings on real three dimensional data in the third ex-

periment. We computed the displacement ﬁeld of two

input frames of human HL-60 cell nucleus with mov-

ing HP1 protein domains. There are global as well as

local movements in the frame pair (see Fig. 4). We es-

timated the ﬂow with RDIA method, α was set to 100.

The size of the input frames was 276×286×106. The

results are illustrated in Fig. 4.

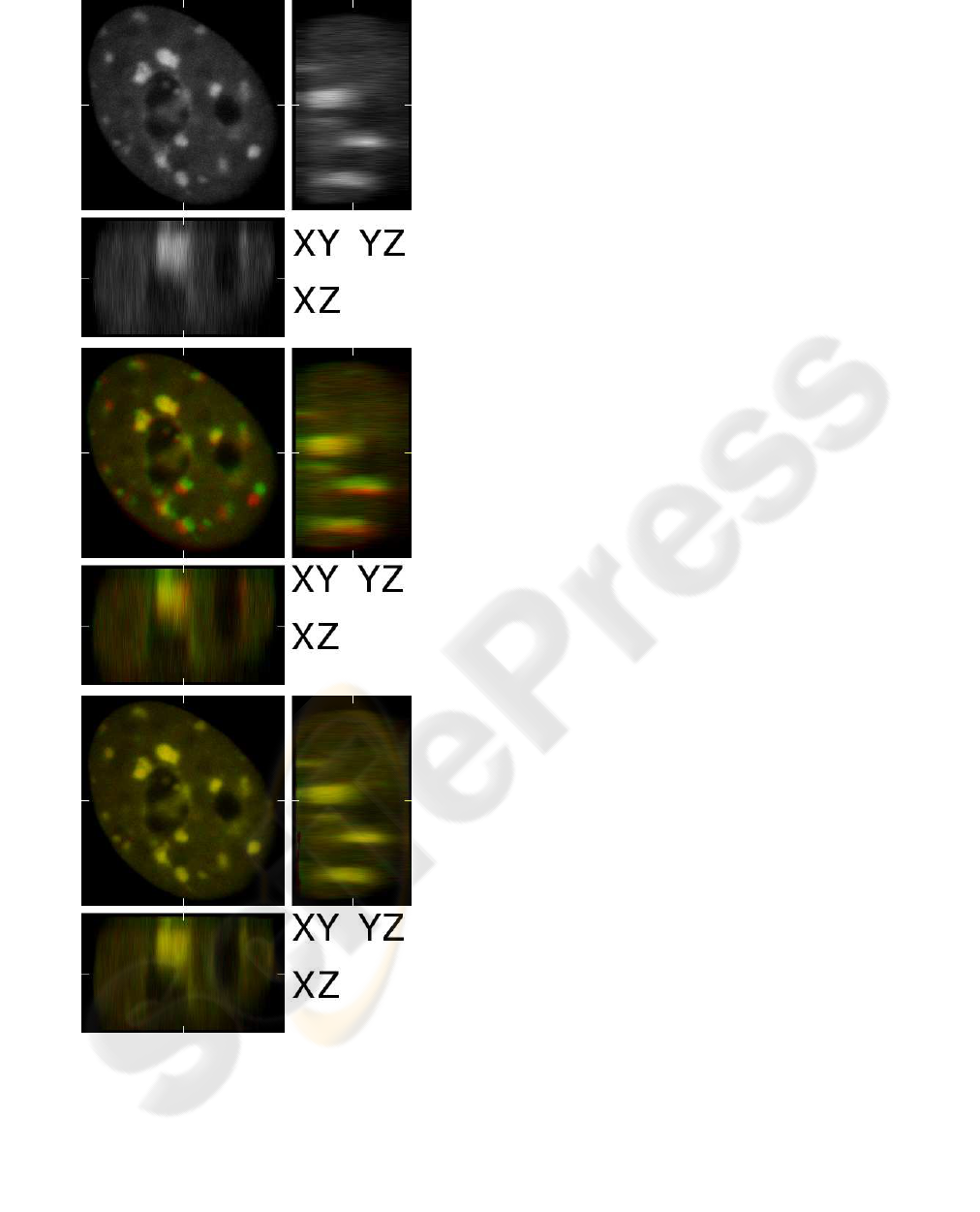
Figure 4: Experiment with real 3D data. Frame

size 276× 286×106. xy, xz and yz cuts on position

(138, 143, 53) are shown. (top). First input frame. (cen-

ter) First input frame (red channel) superimposed on sec-

ond frame (green channel). Correlation is 0.901. (bottom)

The RDIA method with α = 100 computes the ﬂow ﬁeld.

Backward registered second frame (green channel) is su-

perimposed onto ﬁrst frame (red channel). Correlation is

0.991.

The VOF methods were implemented in

C++

lan-

guage and tested on common workstation (Intel Pen-

tium 4 2.6 GHz, 2 GB RAM, Linux 2.6.x). We use the

multigrid framework (Bruhn, 2006) for numerical so-

lution of tested VOF methods. The computations on

two 3D frames of size 276× 286× 106 took from 700

to 920 seconds and needed 1.5 GB of RAM. Compu-

tations on two 2D frames of size 400× 400 took from

13 to 16 seconds and needed 13 MB of RAM.

3.1 Discussion

We found out that the RDIA methods produce slightly

better results than the CLG methods (with respect to

AAE) in both experiments on synthetic live-cell im-

age data. Moreover, RDIA methods are less sensi-

tive to α parameter setting. It became clear that the

smoothing term of RDIA method is more suitable for

the low contrast image sequences. The computed ﬂow

ﬁeld can be easily oversmoothed by the CLG meth-

ods, because they consider the moving objects to be

outliers in the data by particular parameter settings

(larger α).

The use of “gradient” variants of tested method

can slightly improve their performance on live-cell

image data. On the other hand, there is no warranty

that the result will be always better. Actually, the

RDIA method seems to be more sensitive to α param-

eter when using its “gradient” variant. Surprisingly,

the expected improvement of “gradient” variants was

not signiﬁcant even for fading out sequences. We sup-

pose that the gradient constancy assumption does not

help a lot, because the decrease of the intensities be-

tween two consecutive frames is not big. To sum it up,

the 2D tests show that the RDIA method is the most

suitable for our data. Therefore, we used it for the ex-

periment on the 3D real image data. The backward

registered results show perfect match on xy-planes.

The match in xz and yz planes is a little bit worse.

This is caused by the lower resolution of the micro-

scope device in the z axis.

The bleeding-edge multigrid technique allowed us

to get the ﬂow ﬁelds in reasonable times even for 3D

(up to 15 minutes for one frame pair). Small data sets

which consist of only tens of frames of several cells

can be analyzed in order of days on one common PC.

Larger data sets as well as parametric studies in 3D

should be analyzed on a computer cluster.

4 CONCLUSION

We studied state-of-the-art variational optical ﬂow

methods for large displacement for motion tracking

of ﬂuorescently labeled targets in living cells. We fo-

cused on 2D as well as 3D images. Up to our best

knowledge, we tested those methods ﬁrst time in the

literature for three dimensional image sequences.

We showed that these methods can reliably es-

timate large local divergent displacements up to ten

pixels. Moreover, the methods can estimate the global

as well as local movement simultaneously. The vari-

ants of CLG and RDIA method with gradient con-

stancy assumptions did not bring signiﬁcant improve-

ment for our data. The RDIA method produced the

best results in our experiments. We achieved reason-

able computation times (even for three dimensional

image sequences) using the full bidirectional multi-

grid numerical technique.

We plan to perform larger parametric studies on

three dimensional data. This studies need to be per-

formed on computer cluster or grid because of com-

putational demands. Owing to the achieved results,

we also feel conﬁdent in building a motion tracker as

an application based on tested methods. By analyz-

ing computed ﬂow ﬁeld one can extract important bi-

ological data regarding the movement of intracellular

structures.

ACKNOWLEDGEMENTS

This work was partly supported by the Ministry of

Education of the Czech Republic (Grants No. MSM-

0021622419 and LC-535) and by Grant Agency of the

Czech Republic (Grant No. GD102/05/H050).

REFERENCES

Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).

Performance of optical ﬂow techniques. Int. J. Com-

put. Vision, 12(1):43–77.

Briggs, W. L., Henson, V. E., and McCormick, S. F. (2000).

A multigrid tutorial: second edition. Society for In-

dustrial and Applied Mathematics, Philadelphia, PA,

USA.

Bruhn, A. (2006). Variational Optic Flow Computation:

Accurate Modelling and Efﬁcient Numerics. PhD the-

sis, Department of Mathematics and Computer Sci-

ence, Universit

at des Saarlandes, Saarbr

ucken.

Bruhn, A. and Weickert, J. (2005). Towards ultimate motion

estimation: Combining highest accuracy with real-

time performance. In Proc. 10th International Confer-

ence on Computer Vision, pages 749–755. IEEE Com-

puter Society Press.

Bruhn, A., Weickert, J., and Schn

orr, C. (2005). Variational

optical ﬂow computation in real time. IEEE Transac-

tions of Image Processing, 14(5).

Chalﬁe, M., Tu, Y., Euskirchen, G., Ward, W. W., and

Prasher, D. C. (1994). Green ﬂuorescent protein as a

marker for gene-expression. Science, 263(5148):802–

805.

Dawood, M., Lang, N., Jiang, X., and Sch

afers, K. P.

(2005). Lung motion correction on respiratory gated

3d pet/ct images. IEEE Transactions on Medical

Imaging.

de Leeuw, W. and van Liere, R. (2002). Bm3d: Motion es-

timation in time dependent volume data. In Proceed-

ings IEEE Visualization 2002, pages 427–434. IEEE

Computer Society Press.

Fleet, D. J. and Jepson, A. D. (1990). Computation of com-

ponent image velocity from local phase information.

Int. J. Comput. Vision, 5(1):77–104.

Gelfand, I. M. and Fomin, S. V. (2000). Calculus of Varia-

tions. Dover Publications.

Horn, B. K. P. and Schunck, B. G. (1981). Determining

optical ﬂow. Artiﬁcial Intelligence, 17:185–203.

Kozubek, M., Matula, P., Matula, P., and Kozubek, S.

(2004). Automated acquisition and processing of

multidimensional image data in confocal in vivo

microscopy. Microscopy Research and Technique,

64:164–175.

Lin, T. and Barron, J. (1994). Image reconstruction error

for optical ﬂow. In Vision Interface, pages 73–80.

Manders, E. M. M., Visser, A., Koppen, A., de Leeuw,

W., van Driel, R., Brakenhoff, G., and van Driel, R.

(2003). Four-dimensional imaging of chromatin dy-

namics the assembly of the interphase nucleus. Chro-

mosome Research, 11(5):537–547.

Matula, P., Matula, P., Kozubek, M., and Dvo

ak, V. (2006).

Fast point-based 3-d alignment of live cells. IEEE

Transactions on Image Processing, 15:2388–2396.

Nagel, H. H. and Enkelmann, W. (1986). An investigation

of smoothness constraints for the estimation of dis-

placement vector ﬁelds from image sequences. IEEE

Trans. Pattern Anal. Mach. Intell., 8(5):565–593.

Papenberg, N., Bruhn, A., Brox, T., Didas, S., and Weick-

ert, J. (2006). Highly accurate optic ﬂow computa-

tion with theoretically justiﬁed warping. International

Journal of Computer Vision, 67(2):141–158.

Zitov

a, B. and Flusser, J. (2003). Image registration meth-

ods: a survey. 21(11):977–1000.