3D HUMAN TRACKING WITH GAUSSIAN PROCESS

ANNEALED PARTICLE FILTER

Leonid Raskin, Ehud Rivlin and Michael Rudzsky

Computer Science Department,Technion Israel Institute of Technology, Technion City, Haifa, Israel

Keywords: Tracking, Annealed particle filter, Gaussian fields, Latent space.

Abstract: We present an approach for tracking human body parts with prelearned motion models in 3D using multiple

cameras. We use an annealed particle filter to track the body parts and a Gaussian Process Dynamical

Model in order to reduce the dimensionality of the problem, increase the tracker's stability and learn the

motion models. We also present an improvement for the weighting function that helps to its use in occluded

scenes. We compare our results to the results achieved by a regular annealed particle filter based tracker and

show that our algorithm can track well even for low frame rate sequences.

1 INTRODUCTION

This paper presents an approach to 3D people

tracking that enables reduction in the complexity of

this model. We propose a novel algorithm, Gaussian

Process Annealed Particle Filter (GPAPF). In this

algorithm we use nonlinear dimensionality reduction

with the help a Gaussian Process Dynamical Model

(GPDM), (Lawrence (2004), Wang et al. (2005)),

and an annealed particle filter proposed by

Deutscher and Reid (2004). The annealed particle

filter has good performance when working on videos

which were shot with a high frame rate (60 fps, as

reported by Balan et al. (2005)), but performance

drops when the frame rate is lower (30fps). We

show that our approach provides good results even

for the low frame rate (30fps). An additional

advantage of our tracking algorithm is the capability

to recover after temporal loss of the target.

2 RELATED WORKS

One of the common approaches for tracking is using

a Particle Filtering. Particle Filtering uses multiple

predictions, obtained by drawing samples of the

pose and location prior and then propagating them

using the dynamic model, which are refined by

comparing them with the local image data (the

likelihood) (see, for example Isard (1998) or Bregler

et al. (1998)). The prior is typically quite diffused

(because motion can be fast) but the likelihood

function may be very peaky, containing multiple

local maxima which are hard to account for in detail.

For example, if an arm swings past an “arm-like”

pole, the correct local maximum must be found to

prevent the track from drifting (Sidenbladh (2000)).

Annealed particle filter (Deutscher and Reid (2004))

or local searches are ways to attack this difficulty.

There exist several possible strategies for

reducing the dimensionality of the configuration

space. Firstly it is possible to restrict the range of

movement of the subject. This approach has been

pursued by Rohr et al. (1997). The assumption is

that the subject is performing a specific action.

Agarwal et al. (2004) assume a constant angle of

view of the subject. Because of the restricting

assumptions the resulting trackers are not capable of

tracking general human poses.

Another way to cope with high-dimensional data

is to learn low-dimensional latent variable models.

Urtasun et al. (2006) uses a form of probabilistic

dimensionality reduction by Gaussian Process

Dynamical Model (GPDM) (Lawrence (2004), and

Wang et al. (2005)) formulate the tracking as a

nonlinear least-squares optimization problem.

Our approach is similar in spirit to the one

proposed by Urtasun et al. (2006), but we perform a

two stage process. The first stage is annealed particle

filtering in a latent space of low dimension. The

particles obtained after this step are transformed into

the data space by GPDM mapping. The second stage

is annealed particle filtering with these particles in

the data space.

459

Raskin L., Rivlin E. and Rudzsky M. (2007).

3D HUMAN TRACKING WITH GAUSSIAN PROCESS ANNEALED PARTICLE FILTER.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 459-465

 SciTePress

The article is organized as follows. In Section 3

and Section 4 we give short descriptions of particle

filtering and Gaussian fields. In Section 5, we

describe our algorithm. Section 6 contains our

results. The conclusions are in Section 7.

3 FILTERING

The particle filter algorithm was developed for

tracking objects, using the Bayesian inference

framework. Let us denote

x as a hidden state

vector and

y as a measurement in time n . The

algorithm builds an approximation of maximum a

posterior estimate of the filtering distribution:

()

n1:n

px|y where

()

1:n 1 n

y y ,...,y

is the

history of the observation. This distribution is

represented by a set of pairs

() ()

{

}

i=1

x,π

where

() ()

(

)

nnn

π py|x∝

. The main problem is that

the distribution

()

py|x may be very picky.

Often a weighting function

()

wy,x

can be

constructed in a way that it provides a good

approximation of

()

py|x

, and is also easy to

calculate. The main idea in the annealed particle

filter is to use a set of weighting functions instead of

using a single one. A series of

()

{

}

n=0

wy,x is

used, where

()

n+1 n

wy,x represents a smoothed

version of

()

wy,x

. The usual method to

achieve this is by using

()()

nn 0n

wy,x=wy,x

where

()

wy,x is equal to the original weighting

function and

1=β >...>β

. Therefore, each

iteration of the annealed particle filter algorithm

consists of

M steps, in each of these the appropriate

weighting function is used and a set of pairs is

constructed

() ()

{

}

n,m n,m

i=1

x,π . For details see

Deutscher et al. (2004) and Raskin et. al (2007).

4 GAUSSIAN FIELDS

The Gaussian Process Dynamical Model (GPDM)

represents a mapping from the latent space to the

data:

(

)

y=f x , where

∈

x \ denotes a vector in

a d-dimensional latent space and

∈y \ is a vector

that represents the corresponding data in a D-

dimensional space. Gaussian processes stem from

Bayesian formulation, in which the GPDM is

obtained by marginalizing out the parameters and

optimizing the latent coordinates x of the trained

data

y . The model that is used to derive the GPDM

is a mapping with first-order Markov Dynamics:

()

x= aφ x+n

tx,t

ii t-1

y= bψ x+n

ty,t

jj t

∑

(1)

where

x,t

n and

y,t

n are zero-mean Gaussian noise

processes,

[

]

A= a ,a ,... and

[

]

B= b ,b ,... are

weights and

φ and

ψ are basis functions.

For the Bayesian perspective

A and B should

be marginalized out through model average with an

isotropic Gaussian prior on

in closed form to

yield:

()

-1 2 T

pY|X,β =exp-trKYWY

2π K

(2)

where

Y is a matrix of training vectors, X contains

corresponding latent vectors and

K is the kernel

matrix:

(

)

x,x

K=β exp(- x -x )+

y1 ij

2 β

i,j

(3)

W is a scaling diagonal matrix. It is used to account

for the different variances in different data elements.

The hyper parameter

β represents the scale of the

output function,

β represents the inverse of the

RBF's and

-1

β represents the variance of

y,t

For the dynamic mapping of the latent

coordinates

the joint probability density over the

latent coordinate system and the dynamics weights

A are formed with an isotropic Gaussian prior over

the

A , it can be shown (see Wang et al. (2005)) that

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

460

()

(

)

()

-1 T

pX|α =exp-trKXX

x out out

N-1 d

2π K

(4)

where

[

]

,...,

out N

xx= ,

K is a kernel

constructed from

[

]

1N-1

x ,...,x

and

x has an

isotropic Gaussian prior. GPDM uses a

"linear+RBF" kernel with parameter

α :

(

)

x,x

K=α exp(- x -x )+α xx+

12ij

xij

2 α

i,j

(5)

Following Wang et al. (2005)

(

)

(

)

(

)

(

)

(

)

pX,α,β|Y p Y|X,β pX|α p α p β∝

(6)

The latent positions and hyper parameters are found

by maximizing this distribution or minimizing the

negative log posterior:

(

)

()

-1 T

Λ=lnK+trKXX +lnα

x X out out i

-1 2 T

-Nln W + ln K + tr K YW X + lnβ

yY j

∑

(7)

5 GPAPF FILTERING

5.1 The Model

In our work we use a model similar to the one

proposed by Deutscher et al (2004) with some

differences in the annealed schedule and weighting

function. The body model is defined by a pair

{

}

M= L,Γ , where L are the limbs lengths and

Γ are the angles between limbs and the global

location of the body in 3D. The limbs parameters are

constant, and represent the actual size of the tracked

person. The angles represent the body pose and,

therefore, are dynamic. The state is a vector of

dimensionality 29: 3 DoF for the global 3D location,

3 DoF for the global rotation, 4 DoF for each leg, 4

DoF for the torso, 4 DoF for each arm and 3 DoF for

the head. The whole tracking process estimates the

angles in such a way that the resulting body pose

will match the actual pose. This is done by

minimizing the weighting function which is

explained next.

5.2 The Weighting Function

In order to evaluate how well the body pose matches

the actual pose using the particle filter tracker we

have to define a weighting function

()

w,Z

where

is the model's configuration (i.e. angles)

and

Z stands for visual content (the captured

images). Our function is based on a function

suggested by Deutscher et al (2004) with some

changes made to it. We have experimented with 3

different features: edges, silhouette and foreground

histogram. The first feature is the edges. As

Deutscher proposes this feature is the most

important one, and provides a good outline for

visible parts, such as arms and legs. The other

important property of this feature is that it is

invariant to the colour and lighting condition. The

edges maps, in which each pixel is assigned a value

dependent on its proximity to an edge, are calculated

for each image plane. Each part is projected on the

image plane and samples of the

N hypothesized

edge are drawn. A squared probability function is

calculated for these samples:

()

ecv

Ρ ,Z = 1-p ,Z

i=1

j=1

∑

ΓΓ

∑

(8)

where

N is a number of camera views,

Z is

the

i -th image . The

(

)

p,ZΓ

are the edge maps.

However, the problem that occurs using this feature

is that the occluded body parts will produce no

edges. Even the visible parts, such as the arms, may

not produce the edges, because of the colour

similarity between the part and the body. This will

cause

(

)

p,ZΓ to be close to zero and thus will

increase the weighting function. Therefore, a good

pose which may match the visual context may

results in a high value of weighting function and

may be omitted. In order to overcome this problem

we calculate a weight for each image plane. For each

sample point on the edge we estimate the probability

of the point being covered by another body part. Let

N be the number of hypothesized edges that are

drawn for the part

i . The total number of drawn

sample points can be calculated using

i=1

N= N

∑

The weight of the part for the

j -th image plane can

be calculated as following:

(

)

(

)

fg fg

w(,Z)=p,Z/ p,Z

ij ij

k=1 j=1

k=1

∑∑

ΓΓ Γ

∑

(9)

3D HUMAN TRACKING WITH GAUSSIAN PROCESS ANNEALED PARTICLE FILTER

461

where

Γ is the model configuration for part i ,

is the j-th image plane and

()

kij

p,ZΓ is the

probability that the

k -th sample is covered by

another body part. The weighting function therefore

has the following form:

(

)

()

(

)

ecv

Ρ ,Z = 1-p ,Z

bp cv k bp cv

k=1

Ρ ,Z = w( ,Z )Ρ ,Z

ji ji

i=1

j=1

⎛⎞

∑

ΓΓ

⎜⎟

⎝⎠

∑

ΓΓΓ

∑



(10)

The second feature is the silhouette obtained by

subtracting the background from the image. The

foreground pixel map is calculated for each image

plane with background pixels set to 0 and

foreground set to 1 and SSD is computed:

()

Ρ ,Z = 1-p ,Z

i=1

j=1

⎛⎞

∑

ΓΓ

∑

⎜⎟

⎝⎠

ecv

(11)

where

N is the number of different body parts in

the model,

()

p,ZΓ is the value is the foreground

pixel map values at the sample points. The third

feature is the foreground histogram. The reference

histogram is calculated for each body part. It can be

a grey level histogram or three separated histograms

for colour images. Then, on each frame a normalized

histogram is calculated for a hypothesized body part

location and is compared to the referenced one and

the Bhattacharya distance is computed:

(

)

(

)

()

(

)

hyp

ref

P,Z=p ,Zp ,Z

p cv k bp cv bp cv

bins

Ρ ,Z = 1- P ,Z

kbpcv

i=1

j=1 k=1

⎛⎞

ΓΓΓ

⎜⎟

⎝⎠

⎛⎞

∑

ΓΓ

⎜⎟

∑∑

⎜⎟

⎝⎠

(12)

where

()

orig

p,ZΓ is the value of bin

in the

reference histogram, and the

()

hyp

p,ZΓ

is the value

of the same bin on the current frame using the

hypothesized body part location. The main drawback

of that feature is that it is sensitive to changes in the

light condition and the texture of the tracked object.

Therefore, the reference histogram has to be

updated, using the weighted average from the recent

history.

In order to calculate the weighting function the

features are combined together using the following

formula:

efg h

w( ,Z)=exp(-(Ρ (,Z)+Ρ (,Z)+Ρ ( ,Z)))ΓΓΓΓ

(13)

As was stated above, the purpose of the tracker is to

minimize the weighting function.

5.3 GPAPF Learning

The drawback in the particle filter tracker is that a

high dimensionality of the state space causes an

exponential increase in the number of particles that

are needed to be generated in order to preserve the

same density of particles. In our case, the dimension

of the data is 29. In their work Balan et al. (2005)

show that the annealed particle filter can track body

parts with ~125 particles using 60 fps video input.

However, using a significantly lower frame rate (15

fps) causes the tracker to produce bad results and

eventually to lose the target.

The other problem is that once a target is lost (i.e.

the body pose was wrongly estimated, which can

happen for the fast and not smooth movements) it

becomes highly unlikely that the next pose will be

estimated correctly in the following frames. In order

to reduce the dimension of the space we have used

Gaussian Process Annealed Particle Filter (GPAPF).

We use a set of poses in order to create a latent

space with a low dimensionality. The poses are

taken from different sequences, such as walking,

running, punching and kicking. We divide our state

into two independent parts. The first part contains

the global 3D body rotation and translation, which is

independent of the actual pose. The second part

contains only information regarding the pose (26

DoF). We use GPDM to reduce the dimensionality

of the second part. This way we construct a latent

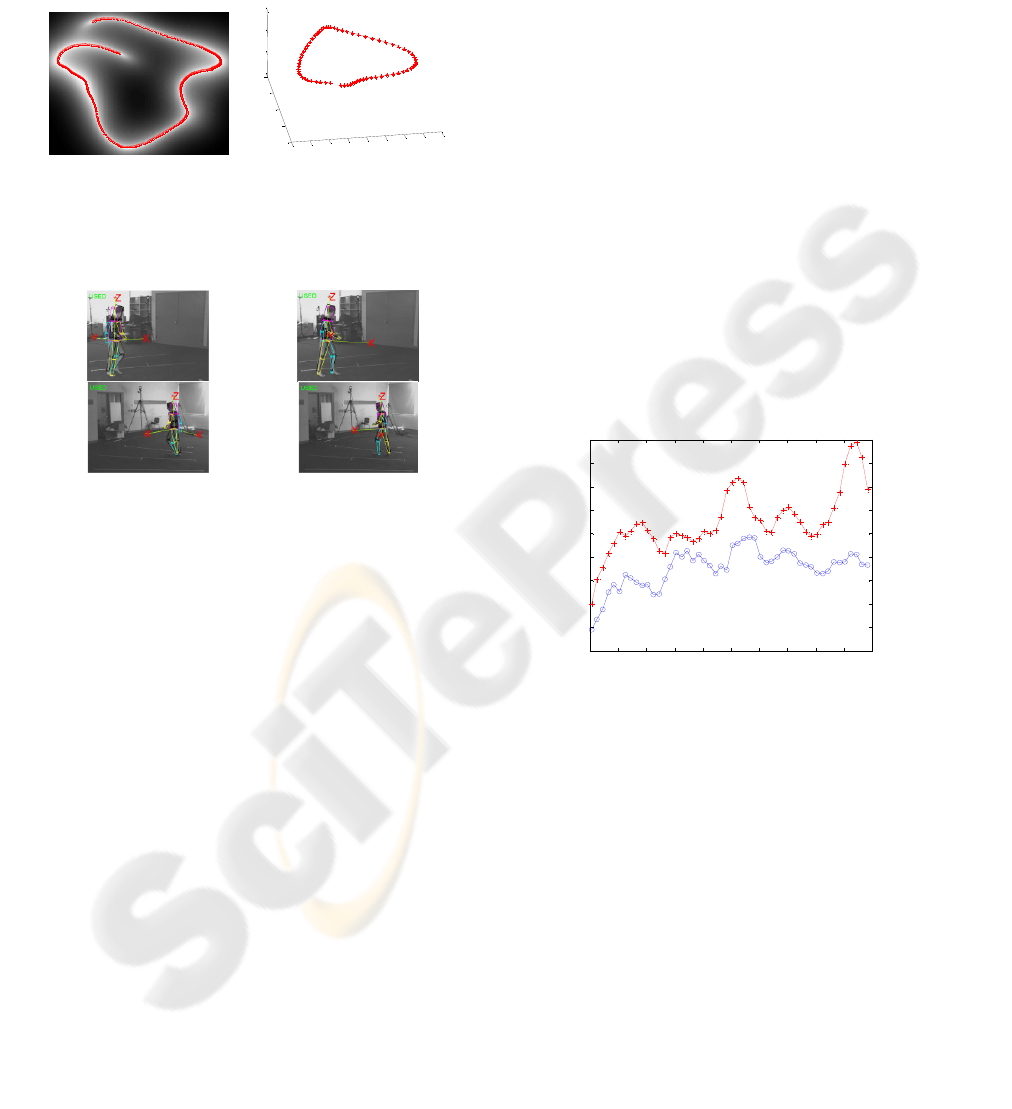
space (Fig. 1). This space has a significantly lower

dimensionality (for example 2 or 3 DoF). Unlike

Urtasun et al. (2006), whose latent state variables

include translation and rotation information, our

latent space includes solely pose information and is

therefore rotation and translation invariant. The

particles are drawn in the latent space. In order to

calculate the weighting function we transform the

data from the latent space to the data space and then

calculate the weighting function as explained above.

However, the latent space is not capable of

producing all the poses; therefore we apply an

additional iteration of the annealed tracker only for

the data space in order to make fine adjustments.

This final iteration is performed using a low

covariance matrix, which is nearly invariant for all

frames rates.

The main difficulty in this approach is that the latent

space is not uniformly distributed. Therefore we are

using a dynamic model, as proposed by Wang et al.

(2005), in order to achieve smoothed transitions

between sequential poses in the latent space.

However, as it is shown in Fig. 1, there are still

some irregularities and discontinuities. Moreover,

while in a regular space the change in the angles is

independent on the actual angle value, in a latent

space this is not the case. Each pose has a certain

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

462

probability to occur and thus the probability to be

drawn as a hypothesis should be dependent on it. For

each particle we can calculate an estimate of the

variance that can be used for generation the new

ones. In the left part of Fig. 1 the lighter pixels

represent lower variance.

-2

-1

-2

-1

-2

-1.5

-1

-0.5

0.5

1.5

-4

-2

Figure 1: The latent space that is learned from different

poses during the walking sequence. Left: the 2D space.

Right: the 3D space. On the left image: the brighter pixels

correspond to more precise mapping.

Frame 137 Frame 141

Figure 2: Losing and finding the tracked target despite the

mis-tracking on the previous frame. Top: camera 1,

Bottom: camera 4.

Another advantage of this method is that the tracker

is capable of recovering after several frames, from

poor estimations. The reason for this is that particles

generated in the latent space are representing valid

poses more authentically. Furthermore because of its

low dimensionality the latent space can be covered

with a relatively small number of particles.

Therefore, most of possible poses will be tested with

emphasis on the pose that is close to the one that was

retrieved in the previous frame. So if the pose was

estimated correctly the tracker will be able to choose

the most suitable one from the tested poses.

However, if the pose on the previous frame was

miscalculated the tracker will still consider the poses

that are quite different. As these poses are expected

to get higher value of the weighting function the

next layers of the annealed will generate many

particles using these different poses. In this way the

pose is likely to be estimated correctly, despite the

mis-tracking on the previous frame (see Fig. 2).

An additional advantage of our approach is that the

generated poses are, in most cases, natural. Poses

generated by the Condensation algorithm or by

annealed particle filtering, where the large variance

in the data space, cause a generation of unnatural

poses. The poses that are produced by the latent

space that correspond to points with low variance

are usually natural and therefore the effective

number of the particles is higher, which enables

more accurate tracking. The drawback of this

approach is that it requires more calculation than the

regular annealed particle filter. The additional

calculations are the result of transformation from the

latent space into the data space.

6 RESULTS

We have tested out algorithm on the sequences

provided by L.Sigal, which are available at his site:

http://www.cs.brown.edu/~ls/Software/index.html.

The sequences contain different activities, such as

walking, boxing etc. which were captured by 7

cameras, however we have used only 4 inputs in our

evaluation. The sequences were captured using the

MoCap system, that provides the correct 3D

locations of the body parts for evaluation of the

results and comparison to other tracking algorithms.

0 20 40 60 80 100 120 140 160 180 200

100

110

Frame number

Predict ion error

Figure 3: The errors of the annealed tracker (red crosses)

and GPAPF tracker (blue circles) for a walking sequence

captured at 30 fps.

The first sequence that we have used was a walk

on a circle. The video was captured at frame rate 120

fps. We have tested the annealed particle filter based

body tracker, implemented by A. Balan (Balan et al.

(2005) ) , and compared the results with the ones

produced by the GPAPF tracker (see Fig. 3 and 4).

The error was calculated, based on comparison of

the tracker's output and the result of the MoCap

system. In Fig. 3 we can see the error graphs,

produced by GPAPF tracker (blue circles) and by

the annealed particle filter (red crosses) for the

walking sequence taken at 30 fps. As can be seen,

the GPAPF tracker produces more accurate

estimation of the body location. Same results were

achieved for 15 fps. In Fig. 4 one can see the actual

3D HUMAN TRACKING WITH GAUSSIAN PROCESS ANNEALED PARTICLE FILTER

463

Ramanan, D., and Forsyth, D. A., 2003 Automatic

Annotation of Everyday Movements. Neural Info.

Proc. Systems (NIPS), Vancouver, Canada.

Sigal, L., Bhatia, S., Roth, S., Black M. and Isard, M.

2004 Tracking loose-limbed people. In CVPR, vol. 1,

pp. 421–428.

Sidenbladh, H., Black, M. and Fleet, D. 2000 Stochastic

tracking of 3d human figures using 2d image motion.

In Proc. ECCV.

Song, Y., Feng, X. and Perona P. 2000. Towards

detection of human motion. In Proc. CVPR, pp 810–

17.

Urtasun, R., Fleet, D. .J., Hertzmann, and A., Fua, P. 2005

Priors for people tracking from small training sets. In

Proc. ICCV, Beijing v1, pp. 403-410.

Urtasun, R., Fleet, D. J., and Fua, P. 2006. 3D People

Tracking with Gaussian Process Dynamical Models.

.In Proc. CVPR'06 , v.1, pp. 238-245.

Wang, J.,Fleet, D. J., and Hetzmann, A. 2005.

Gaussian process dynamical models.In Proc.NIPS.

Vancouver, Canada: pp. 1441-1448.

Raskin, L. Rivlin, E., and Rudzsky M. 2007. 3D Human

Tracking with Gaussian Process Annealed Particle

Filter. Technical.Report. CS-2007-01

3D HUMAN TRACKING WITH GAUSSIAN PROCESS ANNEALED PARTICLE FILTER

465