FACE TRACKING USING CANONICAL CORRELATION ANALYSIS

Jos

e Alonso Yb

nez Zepeda

, Franck Davoine

and Maurice Charbit

Ecole Nationale Sup

erieure des T

ecommunications, Rue Barrault, Paris, France

Compiegne University of Technology, Heudiasyc lab., CNRS, Compi

egne, France

Keywords:

Canonical Correlation Analysis (CCA), Kernel Canonical Correlation Analysis (KCCA), Head Tracking.

Abstract:

This paper presents an approach that incorporates canonical correlation analysis for monocular 3D face track-

ing as a rigid object. It also provides the comparison between the linear and the non linear version (kernel) of

the CCA. The 3D pose of the face is estimated from observed raw brightness shape-free 2D image patches. A

parameterized geometric face model is adopted to crop out and to normalize the shape of patches of interest

from video frames. Starting from a face model ﬁtted to an observed human face, the relation between a set

of perturbed pose parameters of the face model and the associated image patches is learned using CCA or

KCCA. This knowledge is then used to estimate the correction to be added to the pose of the face from an

observed patch in the current frame. Experimental results on tracking faces in long video sequences show the

effectiveness of the two proposed methods.

1 INTRODUCTION

Nowadays video object tracking presents a challeng-

ing problem for video applications such as face-based

biometric person authentication, human computer

interaction, video games, teleconferencing, surveil-

lance, etc. To deal with this problem, vision re-

search groups have proposed several approaches that

can be classiﬁed in two main groups: model-based

and learning-based approaches. In the ﬁrst cate-

gory, tracking algorithms rely on a parametric model

of the object to be tracked. In the second cate-

gory, algorithms assume the availability of a train-

ing set of object examples, and use pattern recog-

nition/classiﬁcation techniques. When working with

video images, we can obtain different features, such

as edges, interest points, grey level intensities or color

histograms, etc. The choice of these features will

depend on the tracked object’s characteristics. The

tracker is traditionally composed of two components:

a representation component to cope with changes in

the target appearance, (caused by a variation in illumi-

nation, an occlusion, a change in orientation or scale,

a facial expression, etc.), and a ﬁltering component

(it adds temporal continuity constraints across frames

and deals with dynamics of the tracked object).

In this paper, we propose a deterministic approach

based on Canonical Correlation Analysis (CCA).

CCA has already been considered for the task of es-

timating an object’s pose from rawbrightness still im-

ages, for example in (Melzer et al., 2003).In our case,

using the work realized in (Davoine and Dornaika,

2005; La Cascia et al., 2000),we combine CCA with

a 3D generic face model to track people’s 3D head

pose as a rigid object. This document is structured

as follows: Section 2 introduces the 3D face model

and how we use it to compute shape-free 2D image

patches. Then, in section 3 we give a description of

Canonical Correlation Analysis (CCA) algorithm in

the linear and non linear form. After that, we present

how we link these concepts to track a face in a video

sequence. Section 4 presents the experimental results

obtained from long video sequences. Finally we give

our conclusions in section 5.

2 FACE REPRESENTATION

The use of a 3D geometric generic model for track-

ing purpose has been widely explored in the computer

396

Alonso Ybáñez Zepeda J., Davoine F. and Charbit M. (2007).

FACE TRACKING USING CANONICAL CORRELATION ANALYSIS.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 396-402

 SciTePress

vision community. It allows to acquire the 3D face

characteristics of a given person and the correspond-

ing texture map to this person’s face. In this section

we present the 3D geometric model used and the way

we employed it to obtain a normalized raw brightness

facial patch.

2.1 3d Geometric Model

In our work, we use the

Candide-3

wireframe model,

proposed by (Ahlberg, 2001). It consists of a group

of n 3D interconnected vertices to describe a face by

means of a small number of triangles, enough to reach

an acceptable realism to represent a face both stati-

cally and dynamically by means of shape and anima-

tion units.

The 3n-vector c consists of the concatenation of

all the vertices, and can be written in terms of the

modiﬁcations that it can be subject to, as:

c = c

+ Aτ

(1)

where Aτ

stands for the dynamic part of the model,

being the columns of A the Animation Units and τ

the animation control vector. The vector c

c+ Sτ

corresponds to the static characteristics of a given per-

son (like the nose size, eye separation distance, etc.),

being

c the standard shape of the Candide model, the

columns of S are the Shape Units, and τ

is the shape

control vector (Ahlberg, 2001). The vectors τ

and τ

are initialized manually, by ﬁtting the Candide shape

over the face in the ﬁrst video frame. Figure 1 shows

the initialization as well as the 3D model with the tex-

ture warped on it in a frontal view and in three ro-

tated views. These views are useful to adjust the z-

component parameters of τ

and τ

during the model

initialization step. The vector τ

is supposed to be

constant: the face is seen as a rigid object during the

tracking process, with a ﬁxed expression.

Figure 1: Candide. model placed over the target face in the

ﬁrst video frame with frontal and three rotated views.

When placing the Candide model over the ﬁrst

frame, we obtain the 3D pose parameters, that we put

in our state vector b, given by:

b = [θ

,θ

] (2)

where the θ elements stand for the rotations and the

t elements stand for the translations that we want to

track. When we place the model over the ﬁrst video

frame, we crop the texture that lies under it and warp

it to the 3D model surface for tracking purposes, as

described below.

2.2 Normalization of the Raw

Brightness Facial Patch

When tracking a moving face in a 3D environment,

we face the problem that its size and geometry are not

constant, making difﬁcult the direct construction of

a facial appearance model. To cope with this prob-

lem, we build a stabilized 2D shape free image patch

(a texture map) to code the facial appearance of the

person facing the camera. This patch is obtained by

warping the rawbrightness image vector lying under

the initialized model c(b) at time t = 0 into a ﬁxed

size (in our case d = 96× 72 pixels) 2D projection of

the reference Candide model without any expression,

i.e. τ

set to zero. The patch is ﬁnally augmented

with the two semi-proﬁle views of the face, as shown

in Figure 2.

We can express this mathematically as it was done

in (Davoine and Dornaika, 2005) as a transforma-

tion

W of the texture observed at each frame Y

For a given state vector b, the observation vector

= W (b, Y

) consists of the columns of the stabi-

lized face image stacked one after the other and nor-

malized such that

∑

i=1

= 1.

10 20 30 40 50 60 70 80 90

Figure 2: Expression-free patch, used to represent the target

face.

3 TRACKING PROPOSITION

The main idea of our algorithm is to estimate the rela-

tion that exists between the variation of the state vec-

tor and the difference between the current observation

vector and the reference vector. To perform this, we

consider two approaches to learn a relation between

a set of perturbed state parameters and the associated

image patches. One is based on Canonical Correla-

tion Analysis, and the other one on kernel CCA to

search for the relationships in the higher dimensional

space. In this section we will brieﬂy introduce CCA

and KCCA, as well as the way we use them to ﬁnd

the model that establishes the relation we are looking

for.

3.1 Canonical Correlation Analysis

Canonical correlation analysis is a way of identifying

and quantifying the linear relationship between two

data sets of random variables. CCA can be seen as the

problem of ﬁnding basis vectors for two sets of vari-

ables, one for Q

and the other for Q

, such that the

correlation between the projections of the variables

onto these basis vectors are mutually maximized.

Let A

and A

be the centered data sets corre-

sponding to the Q

data matrix of dimension m × n

and Q

the data matrix of dimension m × p respec-

tively. The maximum number of correlations that can

be found is equal to the minimum of the data sets’

column dimension min(n, p). If we map our data to

the directions w

and w

we obtain, for each pair of

directions, two new vectors deﬁned as:

= A

and z

= A

(3)

These vectors are called the scores (Borga et al.,

1997; Dehon et al., 2000; Weenink, 2003), and we

are interested in ﬁnding the correlation between them,

which is deﬁned as:

ρ =

(4)

Our problem is to ﬁnd the vectors w

and w

that

maximize (4) subject to the constraints z

= 1 and

= 1. In order to do that, we formulate our prob-

lem in a Lagrangian form.

As we have the data matrices A

and A

we can

use the method proposed in (Weenink, 2003), to re-

duce the number of matrix operations, where they per-

form the singular value decomposition of the data ma-

trices A

= U

and A

= U

, then they

introduce the singular value decomposition: U

UDV

, to ﬁnally get:

= V

−1

U and W

= V

−1

V (5)

where we denote W

and W

as the matrices contain-

ing respectively the canonical correlation basis vec-

tors w

and w

The main advantage of this procedure is that it

avoids the estimation of the covariance matrices and

the calculation of the corresponding inverses, and in-

stead, we need to perform three singular value decom-

positions, which are numerically more robust.

3.2 Tracking Implementation Using the

Cca

Once we have shown the CCA, we can proceed to

describe our tracking algorithm. It consists of three

steps: Initialization, Training process, and Tracking

process.

Initialization. During the initialization we place the

Candide model over the ﬁrst video frame Y

, and ad-

just it to the person’s characteristics as previously de-

scribed, obtaining the state vector b

, and the refer-

ence vector at time t = 0 as:

(ref )

W (b

) (6)

Training process. It consists of obtaining a linear

model containing the relation between the variation in

the state vector ∆b

and the vector resulting from the

difference of the observation vector and the reference

vector x

− x

(ref )

To obtain this relationship, we need to deﬁne the

data matrices A

and A

. The matrix A

contains the

difference between the m training observation vectors

Training

W (b

Training

) and the reference x

(ref )

and the matrix A

contains the corresponding vari-

ation in the state vector obtained from the relation

∆b

Training

= b

Training

−b

. The m training points were

chosen empirically from a non-regular grid around the

vector state obtained at initialization. From these ma-

trices we can obtain the canonical correlation basis

vectors as described before. Once we have obtained

this basis, the general solution consist in doing a lin-

ear regression between z

and z

. However, if we de-

velop 4 for each pair of directions with the assump-

tions made above, we arrive at kA

− A

2(1− ρ) similarly as in (Hardoon et al., 2004). In our

case, we have ρ ≈ 1 (from experimental data), so, we

have the following relation:

= A

(7)

that simpliﬁes the obtention of our model by avoiding

the linear regression needed when ρ 6= 1.

We suppose that the learned relations from the ma-

trices A

and A

are valid for the current ∆b

and

− x

(ref )

) in (7), then we can then write:

∆b

= (x

− x

(ref )

(8)

If we write the result for all the pair of directions in

a matrix form, we can replace equations (5) in the last

equation, and after some mathematical manipulation,

we arrive at:

∆b

= (x

− x

(ref )

)G (9)

where the G matrix, that encodes the linear model

used by our tracker, is given by:

G = V

−1

(10)

It is important to notice that the matrix G is only

valid for a certain rotation interval and it is very de-

pendent on the training points used and on the initial-

ization of the Candide model.

Tracking process. The tracking process estimates

the state vector variation ∆b

from the difference be-

tween the current observation vector and the reference

vector by means of the G matrix built during the train-

ing process. To perform this estimation, we obtain the

current observation vector, which depends on the cur-

rent video frame Y

and the state vector at the preced-

ing instant b

t−1

as:

W (b

t−1

) (11)

and then, we obtain the difference between the obser-

vation vector and the the reference vector x

(ref )

. Then

we use this difference vector and the G matrix to up-

date the state vector as:

= b

t−1

+ (x

− x

(ref )

)G (12)

With

, we get a new observation vector

W (

) and we compare it with the reference x

(ref )

to compute the error measure:

e(b

) =

∑

i=1

ˆx

i,t

− x

(ref )

i,t

(ref )

i,t

(13)

where σ

is the variance of the reference vector. If

e(b

) is bigger than a certain threshold, we use the

state vector estimated

in (12) and obtain again an

error measure. We iterate a ﬁxed number of times (5,

in practice). Once the iterations are done, and in order

to increase the robustness of the tracker to weak illu-

mination changes, we proceed to update the reference

vector and its variance according to:

(ref )

t+1

= αx

(ref )

+ (1− α)

(14)

t+1

= ασ

+ (1− α)(

− x

(ref )

)

(15)

being α = 0.99 obtained empirically.

This approach is useful when we work with data

that has a linear behavior. In our case this linear ap-

proach showed a good performance, but for compari-

son reason, we studied also the use of the kernel CCA,

to ﬁnd out if an approach that can cope with non linear

relations, can outperform the linear approach previ-

ously described. In the following part, we will present

the Kernel Canonical Correlation Analysis and the al-

gorithm used for tracking purposes.

3.3 Kernel Canonical Correlation

Analysis

The main idea behind kernel methods is that we can

still apply a linear method to analyse a given data set,

but ﬁrst we need to map this data into a high dimen-

sional feature space. Thus, using kernel-functions we

can formulate our problem as a non-linear version of

the original one with the advantage that the complex-

ity of the transformed problem is not linked to the

feature space dimension, but to the training data set

dimension, which means that we can use kernel trans-

formations to feature spaces of high dimensionality.

If we deﬁne A

and A

as the centred data sets

of dimension m × n and of dimension m × p respec-

tively, we can apply the CCA to the vectors φ(A

) =

(φ(a

(1)

)...φ(a

(1)

)) and θ(A

) = (θ(a

(2)

)...θ(a

(2)

)),

according to the kernel trick (see (Melzer et al.,

2003)), which are two non linear mappings.

Then we deﬁne the kernel matrices K,L by K

φ(a

(1)

)φ(a

(1)

)

and L

= θ(a

(2)

)θ(a

(2)

)

, with f

and

which can be seen as the coefﬁcients of the linear

expansion of the principal vectors w

and w

in terms

of the transformed data, i.e., w

= φ(A

)

and w

θ(A

)

We can then deﬁne as for the CCA the correlation

between the transformed data as:

ρ =

(16)

which we maximize in the same way as for the CCA.

The problem that arises from KCCA is that we

work with a ﬁnite number of points in a high dimen-

sional feature space, which can lead us to useless re-

sults. To force useful solutions we introduce a pe-

nalizing factor in the norms of the associated weights

which leads us to the eigenvalue equations (for more

details see (Hardoon et al., 2004)):

(K+ κI)

−1

L(L+ κI)

−1

= ρ

(17)

(L+ κI)

−1

K(K+ κI)

−1

= ρ

(18)

We can then obtain the vectors f

and g

as the

eigenvectors of this equations.

3.4 Algorithm Implementation Using

the Kcca

As for the CCA, we can divide the algorithm in three

parts, the initialization being exactly the same as in

the case of the CCA. For the training process, we need

to obtain vectors f

and g

as described in the last

section, using the same data matrices as the ones de-

scribed for the CCA approach. It is important to point

out that in the case of the variation vectors, we did not

use any kernel. Once this is done, the starting point

for the tracking is equation (7) that can be developed

according to the KCCA as:

≈ A

(19)

If we develop as above, we can assume that the

tracking data satisﬁes also this equation and after

some mathematical manipulation we arrive at:

∆b

= K

)

−1

(20)

Here we can see that the K

corresponds to the

kernel matrix at time t obtained between the training

vectors x

(i)

−1

W (b

(i)

−1

), i = 1...m and the actual

patch x

W (b

t−1

). However, for the algorithm

implementation, we compute a linear regression be-

tween the result of the product of the matrix kernel

and the variation vector Q

, so that we have the

actualization equation:

∆b

= K

G (21)

being the matrix G obtained from the training kernel

matrix K. We use in our case the Gaussian RBF ker-

nel function:

K(x

) = exp(−

− x

2σ

) (22)

In our experiments, the two parameters σ and κ

are set respectively to 0.009 and 0.003. They were

obtained empirically from simulations using training

sequences, and based on the method used in (Melzer

et al., 2003) to estimate a starting point.

4 RESULTS

In order to evaluate our proposals, we implemented

our algorithm on a PC with a 3.0 GHz Intel Pen-

tium IV processor and a NVIDIA Quadro NVS 285

graphics card. The non optimized implementation

uses OpenGL for the texture mapping and OpenCV

for the video capture. We have used the video se-

quences used by (La Cascia et al., 2000)

, the an-

notated talking face video

, as well as some video

sequences made with a Winnov analog video camera

XC77B/320.

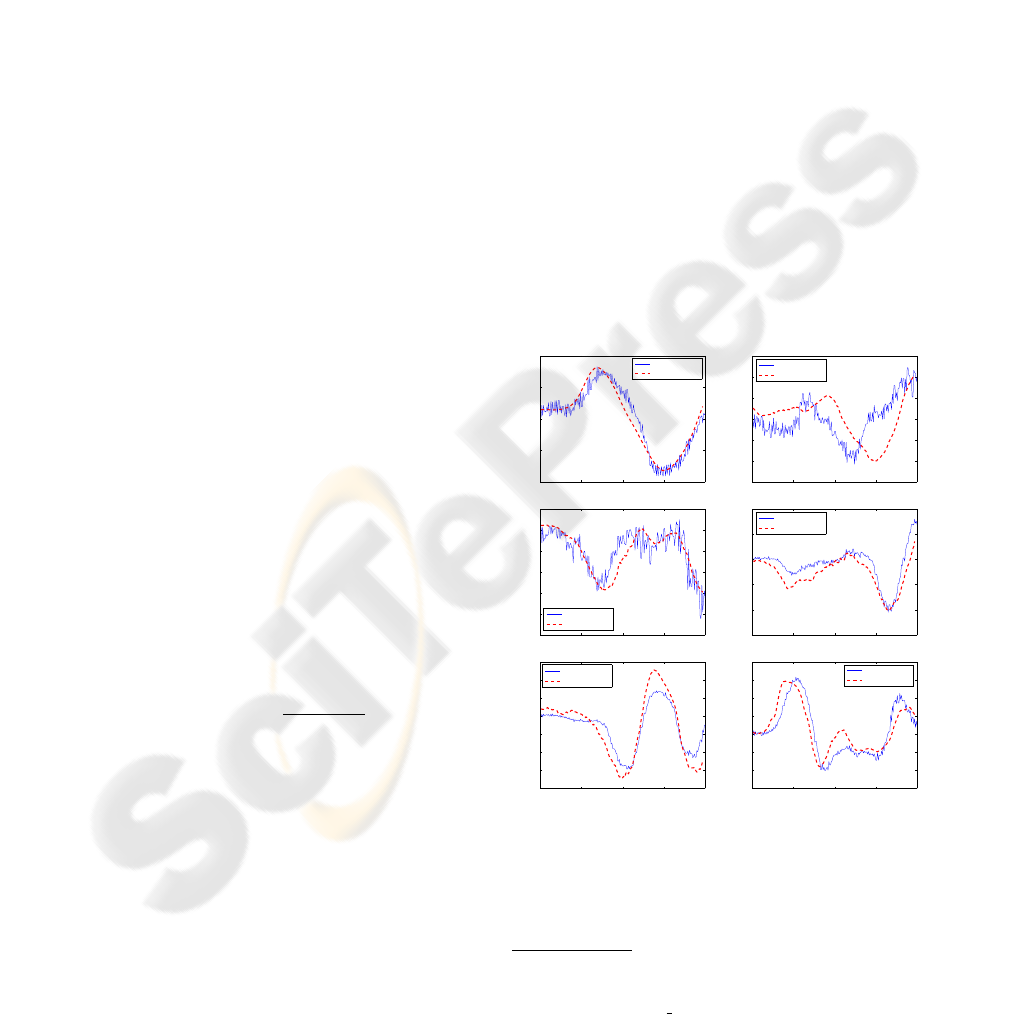
Figure 3 shows the results obtained from the CCA

algorithm. It depicts the state vector estimated com-

pared to the ground truth provided by (La Cascia

et al., 2000). We see that the performance of our

tracker is close to the ground truth. However, the co-

ordinate system used by our system is not the same as

that of the data given, specially for the translationand

hence compare them we had normalized both data.

There is also a issue with the rotation axes, which are

not located at the same point in our system (where

the three axes cross close to the nose, due to the Can-

dide model’s speciﬁcation), and in the ground truth

data provided (where the 3D magnetic tracker was at-

tached on the subjects head). This discrepancy caused

principally the difference in the translation parame-

ters, because what in one system represents a rotation,

in the other system represents a rotation and a trans-

lation.

0 50 100 150 200

−2

−1

frame

X position normalized

Ground Truth

Estimation

0 50 100 150 200

−3

−2

−1

frame

Y position normalized

Ground Truth

Estimation

0 50 100 150 200

−4

−3

−2

−1

frame

Scale normalized

Ground Truth

Estimation

0 50 100 150 200

−30

−20

−10

frame

Rx in degrees

Ground Truth

Estimation

0 50 100 150 200

−40

−30

−20

−10

frame

Ry in degrees

Ground Truth

Estimation

0 50 100 150 200

−15

−10

−5

frame

Rz in degrees

Ground Truth

Estimation

Figure 3: Ground truth compared with the CCA algorithm’s

results.

Figure 4 depicts some video frames taken from

two tracked videos from (La Cascia et al., 2000) and

http : //www.cs.bu.edu/groups/ivc/HeadTracking/

http : //www− prima.inrialpes. fr/FGnet/data/01−

TalkingFace/talking

face.html

a webcam video. The CCA and the KCCA algorithm

performance did not present any problem when track-

ing the head in these video sequences, especially be-

cause there are not facial gesture involved. In the case

of the webcam video, we succeeded in tracking cor-

rectly rotations in the y plane going as far as ±35

◦

However, when trying to go further, the algorithm

could not estimate the correct variation of the angle

and got lost.

Another test has been performed using a part of

the talking face video. This video presents slight head

pose changes compared with the previous employed

videos, but it presents more signiﬁcant movements

due to facial gesture. This video shows a person en-

gaged in conversation in front of a camera. It comes

with ground truth data that consist of characteristic

face points annotated semi-automatically. From the

68 annotated points, we chose the 52 points that were

closer to the corresponding Candide model’s points.

Because these points were not exactly the same as the

ones given in the ground truth database, there existed

an initial distance between the points. In order to mea-

sure the behavior of our algorithm, we calculated the

standard deviation of this distance, as shown in Figure

5. We can see that the points that presented the higher

variance were those in the head’s contour.

In Figure 6 we can see the result of tracking the

talking face over 1720 frames. The importance of this

ﬁgure is that we can see the evolution of the error dur-

ing the video. We have seen that the peaks appearing

in this ﬁgure represent the moments when there was

a facial gesture or a important rotation. However, as

seen in the frames displayed, we can cosider that these

peaks does not represent a signiﬁcant error between

the state vector estimated and the real head pose.

The time required per frame processing depends

on the video size, as can be seen in the table 1. In that

table we show also the comparison between the CCA

and the KCCA implementation.

Table 1: Comparation of time per frame.

Video’s size [pixels] time per frame [ms]

CCA 640× 480 147.6

CCA 720× 576 179.5

KCCA 320× 240 2486.7

5 CONCLUSIONS

We have seen that the pose tracking is well performed

with the two trackers implemented. They managed to

follow the head movements in long video sequences

of more than 1700 frames. The main advantage of this

algorithm is that it is simple and proved to be robust

to facial gesture. However, we observed from simu-

lations that the effectiveness of this kind of tracker is

dependant on the mask initialization, i.e., the 3D mask

must be correctly initialized, in pose and in facial fea-

tures at the ﬁrst frame, otherwise, the tracker can get

lost because the model affects directly the texture ex-

traction and consequently the state vector predictor.

The results obtained by means of the CCA and the

KCCA did not present a signiﬁcant difference. How-

ever, if we consider the computation time required for

the KCCA algorithm, which was 10 times slower than

the CCA algorithm, we can conclude that for the type

of data we use, it is better to use the linear approach.

In our future work we will add the gesture track-

ing, based on the CCA approach, principally for

tracking the mouth and eyebrows, and based on the

work of (La Cascia et al., 2000), we will include a

robust measure to the tracking algorithm.

REFERENCES

Ahlberg, J. (2001). Candide-3 – an updated parameterized

face. Technical Report LiTH-ISY-R-2326, Linkoping

University, Sweden.

Borga, M., Landelius, T., and Knutsson, H. (1997). A uni-

ﬁed approach to PCA, PLS, MLR and CCA. Report

LiTH-ISY-R-1992, ISY, SE-581 83 Link

oping, Swe-

den.

Davoine, F. and Dornaika, F. (2005). Real-Time Vision for

Human Computer Interaction, chapter Head and Fa-

cial Animation Tracking using Appearance-Adaptive

Models and Particle Filters. Springer Verlag.

Dehon, C., Filzmoser, P., and Croux, C. (2000). Robust

methods for canonical correlation analysis. In Kiers,

H., Rasson, J., Groenen, P., and Schrader, M., editors,

Data Analysis, Classiﬁcation, and Related Methods,

pages 321–326. Springer-Verlag.

Hardoon, D., Szedmak, S., and Shawe-Taylor, J. (2004).

Canonical correlation analysis; an overview with ap-

plication to learning methods. Neural Computation,

16:2639–2664.

La Cascia, M., Sclaroff, S., and Athitsos, V. (2000). Fast,

reliable head tracking under varying illumination: an

approach based on registration of texture-mapped 3D

models. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(2):322–336.

Melzer, T., Reiter, M., and Bischof., H. (2003). Appearance

models based on kernel canonical correlation analysis.

Pattern Recognition, 36(9):1961–1973.

Weenink, D. (2003). Canonical correlation analysis. In

Proceedings of the Institute of Phonetic Sciences of

the University of Amsterdam, Netherlands, volume 25,

pages 81–99.

Figure 4: Results from tracking three video sequences using

the CCA algorithm in the ﬁrst ﬁve images, and the KCCA

algorithm in the last one.

0 10 20 30 40 50 60

Point number

Standard deviation

Contour

Eyebrows

Eyes

Nose

Mouth

Figure 5: Standard deviation of the points provided for the

talking face video sequence.

0 500 1000 1500

frame

Point to point error

378

991

712

Figure 6: Mean point to point error, and three frames of the

sequence corresponding, to frame 378 to frame, 712, and

991 respectively, using the CCA algorithm.