AUTOMATIC KERNEL WIDTH SELECTION FOR NEURAL
NETWORK BASED VIDEO OBJECT SEGMENTATION
Dubravko Culibrk
University of Novi Sad
Novi Sad, Serbia
Daniel Socek, Oge Marques, Borko Furht
Department of Computer Science and Engineering, Florida Atlantic University
Boca Raton FL 33431, USA
Keywords:
Video processing, Object segmentation, Background modeling, BNN, Neural Networks.
Abstract:
Background modelling Neural Networks (BNNs) represent an approach to motion based object segmentation
in video sequences. BNNs are probabilistic classifiers with nonparametric, kernel-based estimation of the
underlying probability density functions. The paper presents an enhancement of the methodology, introducing
automatic estimation and adaptation of the kernel width.
The proposed enhancement eliminates the need to determine kernel width empirically. The selection of a
kernel-width appropriate for the features used for segmentation is critical to achieving good segmentation re-
sults. The improvement makes the methodology easier to use and more adaptive, and facilitates the evaluation
of the approach.
1 INTRODUCTION
Object segmentation is a basic task in the domain of
digital video processing. Diverse applications, such
as scene understanding, object-based video encoding,
surveillance applications and 2D-to-pseudo-3D video
conversion, rely on the ability to extract objects from
video sequences.
The research into object segmentation for video
sequences grabbed from a stationary camera has
yielded a number of approaches based on the detec-
tion of the motion of objects. The approaches of
this class scrutinize the changes observed between
the consecutive frames of the sequence to detect pix-
els which correspond to moving objects. The task is
particularly difficult when the segmentation is to be
done for natural scenes where the background con-
tains shadows, moving objects, and undergoes illumi-
nation changes.
For purposes of automated surveillance and scene
understanding it is often of more interest not only to
detect the objects moving in the scene, but to distin-
guish between two classes of objects:
• Background objects corresponding to all objects
that are present in the scene, during the whole se-
quence or longer than a predefined period of time.
• Foreground objects representing all other objects
appearing in the scene.
The goal of the foreground segmentation is to sep-
arate pixels corresponding to foreground from those
corresponding to background.
Background Modeling Neural Network (BNN)
represents a probabilistic approach to foreground seg-
mentation(Culibrk et al., 2006). The network is a
Bayes rule based unsupervised classifier designed to
enable the classification of a single pixel as pertinent
to foreground or background. A set of networks is
used to classify all the pixels within the frame of the
sequence.
The networks incorporate kernel-based estimators
(Mood and Graybill, 1962) for probability density
functions used to model the background. The net-
works are general in terms of the features of a pixel
used to perform the classification, such as RGB val-
ues or intensity values. However, the accuracy of the
process depends on the ability to determine the ap-
propriate width for the estimator kernels. The pro-
cess relies on empirical data and involves tedious ex-
perimentation. In addition the BNNs are unable to
adapt to conditions occurring in specific sequences.
Rather, a single value is typically used whenever the
same features are used as basis for segmentation. Fur-
472
Culibrk D., Socek D., Marques O. and Furht B. (2007).
AUTOMATIC KERNEL WIDTH SELECTION FOR NEURAL NETWORK BASED VIDEO OBJECT SEGMENTATION.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 472-479
Copyright
c
 SciTePress

thermore, the complexity of the process of evaluation
of a segmentation algorithm depends directly on the
number of parameters that need to be specified (Wirth
et al., 2006). Thus, reducing the number of param-
eters not only makes the methodology easier to use
and more adaptive, it facilitates the evaluation of the
approach.
In this paper, an extension of the BNN methodol-
ogy is proposed to incorporate automatic selection of
the appropriate kernel width. The proposed enhanced
BNNs do not suffer from the above mentioned short-
comings of the fixed-kernel-width BNNs and achieve
comparable segmentation performance.
The rest of the paper is organized as follows: Sec-
tion 2 provides a survey of related published work.
Section 3 contains a short description of BNNs. The
proposed enhancement of the BNNs is described in
Section 4. Section 5 is dedicated to the presentation
of experimental evaluation results. Section 6 contains
the conclusions.
2 RELATED WORK
Early foreground segmentation methods dealing with
non-stationary background are based on a model of
background created by applying some kind of low-
pass filter on the background frames. The high-
frequency changes in intensity or color of a pixel are
filtered out using different filtering techniques such
as Kalman filters (Karmann and von Brandt, 1990) to
create an approximation of background in the form of
an image (reference frame). The reference frame is
updated with each new frame in the input sequence,
and used to segment the foreground objects by sub-
tracting the reference frame from the observed frame
(Rosin, 1998). These methods are based on the most
restrictive assumption that observe pixel changes due
to the background are much slower than those due
to the objects to be segmented. Therefore they are
not particularly effective for sequences with high-
frequency background changes, such as natural scene
and outdoor sequences.
Probabilistic techniques achieve superior results
in case of such complex-background sequences.
These methods rely on an explicit probabilistic model
of the background, and a decision framework allow-
ing for foreground segmentation. A Gaussian-based
statistical model whose parameters are recursively up-
dated in order to follow gradual background changes
within the video sequence is proposed in(Boult et al.,
1999). More recently, Gaussian-based modelling was
significantly improved by employing a Mixture of
Gaussians (MoG) as a model for the probability den-
sity functions (PDFs) related to the distribution of
pixel values. Multiple Gaussian distributions, usu-
ally 3-5, are used to approximate the PDFs (Ellis and
Xu, 2001)(Stauffer and Grimson, 2000). The param-
eters of each Gaussian curve are updated with each
observed pixel value. If an observed pixel value is
within the 2.5 standard deviations (σ) from the mean
(µ) of a Gaussian, the pixel value matches the Gaus-
sian (Stauffer and Grimson, 2000). The parameters
are updated only for Gaussians matching the observed
pixel value, based on the following Equations:
µ
t
= (1−ρ)∗µ
t−1
+ ρ ∗X
t
(1)
σ
2
t
= (1−ρ) ∗σ
2
t−1
+ ρ ∗(X
t
−µ
t
)
T
∗(X
t
−µ
t
) (2)
where
ρ = ℵ(X
t
, µ
t−1
, σ
t−1
) (3)
and ℵ is a Gaussian function and X
t
is a pixel value
observed at time t. Equations 1 - 3 express a causal
low-pass filter applied to the mean and variance of the
Gaussian.
Using a small number of Gaussians leads to
a rough approaximation of the PDFs involved.
Due to this fact, MoG achieves weaker results
for video sequences containing non-periodical back-
ground changes (e.g. due to waves and water sur-
face illumination, cloud shadows, and similar phe-
nomena), as was reported in (Li et al., 2004). The
Gaussian-based models are parametric in the sense
that they incorporate underlying assumptions about
the probability density functions (PDFs) they are try-
ing to estimate.
In 2003, Li et al. proposed a method for fore-
ground object detection employing a Bayes decision
framework (Li et al., 2004). The method has shown
promising experimental object segmentation results
even for the sequences containing complex variations
and non-periodical movements in the background.
The primary model of the background used by Li
et al. is a background image obtained through low
pass filtering. However, the authors use a probabilis-
tic model for the pixel values detected as foreground
through frame-differencing between the current frame
and the reference background image. The probabilis-
tic model is used to enhance the results of primary
foreground detection. The probabilistic model is non-
parametric since it does not impose any specific shape
to the PDFs learned. However, for reasons of effi-
ciency and improving results the authors applied bin-
ning of the features and assigned single probability to
each bin, leading to a discrete representation of PDFs.
The representation is equivalent to a kernel-based es-
timate with quadratic kernel. The width of the kernel
used was determined empirically and remained fixed
in all the reported experiments(Li et al., 2004). The

system achieved performance better than that of the
mixture of 5 Gaussians in the results presented in the
same publication. However, when larger number of
Gaussians is used, MoG achieved better performance
(Culibrk, 2006). A nonparametric kernel density es-
timation framework for foreground segmentation and
object tracking for visual surveillance has been pro-
posed in (ElGammal et al., 2002). The authors present
good qualitative results of the proposed system, but do
not evaluate segmentation quantitatively nor do they
compare their system with other methods. The frame-
work is computationally intensive as the number of
kernels corresponds to the number of observed pixel
values. The width of the kernels is adaptive and they
use the observed median of absolute differences be-
tween consecutive pixel values. The rationale for the
use of median is the fact that its estimate is robust
to small number of outliers. They assume Gaussian
(normal) distribution for the differences and establish
a relation between the estimated median and the width
of the kernel:
σ =
m
0.68
√
2
(4)
where m is the estimated median.
The approach based on background modelling
neural networks was proposed in (Culibrk et al.,
2006). The networks employ represent a biologically
plausible implementation of Bayesian classifiers and
nonparametric kernel based density estimators. The
weights of the network store a model of background,
which is continuously updated. The PDF estimates
consist of fixed number of kernels, which have fixed
width. The appropriate width of the kernels is deter-
mined empirically. The kernel width depends on the
features used to achieve segmentation. Results supe-
rior to those of Li et al. and MoG with 30 Gaussians
are reported in (Culibrk, 2006).The BNNs address
the problem of computational complexity of the ker-
nel based background models by exploiting the paral-
lelism of neural networks.
3 BACKGROUND MODELING
NEURAL NETWORK (BNN)
Background Modeling Neural Network (BNN) is a
neural network classifier designed specifically for
foreground segmentation in video sequences. The
network is an unsupervised learner. It collects statis-
tics related to the dynamic processes of pixel-feature-
value changes. The learnt statistics are used to clas-
sify a pixel as pertinent to a foreground or background
object in each frame of the sequence.
Note that a video sequence can be viewed as
a set of pixel feature values changing in time, so-
called pixel processes (Stauffer and Grimson, 2000).
Pixel feature values are, in general, vectors in multi-
dimensional space, such as RGB space. Probabilis-
tic motion-based foreground segmentation methods,
including the BNN approach, rely on a supposition
derived from the definitions of foreground and back-
ground stated in Section 1:
Pixel (feature) values corresponding to back-
ground objects will occur most of the time, i.e. more
often than those pertinent to the foreground.
Thus, if a classifier is able to effectively distin-
guish between the values occurring more frequently
than others it should be able to achieve accurate seg-
mentation. The BNN classifier strives to estimate the
probability of a pixel value X occurring at the same
time as the event of a background or foreground ob-
ject being located at that particular pixel. In terms of
probability theory, the BNN tries to estimate the joint
probability p(b, X) of background b and pixel value
X occurring at the pixel the BNN is trying to classify
and the analogous joint probability p( f, X) for fore-
ground.
By virtue of the Bayes rule, the classification cri-
terion used in BNN is the following:
p(b|X)p(X) − p( f|X)p(X) > 0 (5)
where p( f|X) and p(b|X) represent estimated con-
ditional PDFs of an observed pixel value X indicat-
ing a foreground and background object, respectively.
p(X) is the estimated PDF of a feature value occur-
ring.
In the structure of BNN, shown in Figure 1, three
distinct subnets can be identified. The classification
subnet is a central part of BNN concerned with ap-
proximating the PDF of pixel feature values belong-
ing to background/foreground. It is a neural network
implementation of a Parzen (kernel based) estimator
(Parzen, 1962). The estimation is discussed in more
detail in Section 4.
The classification subnet contains three layers of
neurons. Input neurons of this network simply map
the inputs of the network, which are the values of the
feature vector for a specific pixel, to the pattern neu-
rons. The output of the pattern neurons is a nonlin-
ear function of Euclidean distance between the input
of the network and the stored pattern for that specific
neuron:
p
i
= exp[−
(w
i
−x
t
)
T
(w
i
−x
t
)
2σ
2
] (6)
where w
i
is the vector of weights between the input
neurons and the i-th pattern neuron, x
t
is the pixel
feature value vector and p
i
is the output of the i-th

Figure 1: Structure of Background Modeling Neural Network.
pattern neuron. The only parameter of this subnet is
the kernel width (σ), sometimes dubbed the smooth-
ing parameter, which is used to control the shape of
the nonlinear function.
The output of the summation units of the classi-
fication subnet is the sum of their inputs. The sub-
net has two summation neurons: one to calculate the
probability of the observed pixel value corresponding
to background and the other to calculate the probabil-
ity of the value pertaining to foreground, correspond-
ing to products in criterion 5.
Weights between the pattern and summation neu-
rons are used to store the confidence with which a
pattern belongs to the background/foreground. The
weights of these connections are updated with each
new pixel value received (i.e. with each frame), ac-
cording to the following recursive equations:
w
t+1
ib
= f
c
((1−
β
P
) ∗w
t
ib
+ MA
t
β) (7)
w
t+1
if
= 1−w
t+1
ib
(8)
where w
t
ib
is the value of the weight between the i-th
pattern neuron and the background summation neu-
ron at time t, w
t
if
is the value of the weight between
the i-th pattern neuron and the foreground summation
neuron at timet, β is the learning rate, P is the number
of the pattern neurons of BNN, f
c
is a clipping func-
tion defined by (9) and MA
t
indicates the neuron with
the maximum response (activation potential) at frame
t, according to (10).
f
c
(x) =

1, x > 1
x, x ≤1
(9)
MA
t
=

1, for neuron with maximum response;
0, otherwise.
(10)
Equations 7 - 10 express the notion that whenever
an instance pertinent to a pattern neuron is encoun-
tered, the probability that that pattern neuron is acti-
vated by a feature value vector belonging to the back-
ground is increased. Naturally, if that is the case, the
probability that the pattern neuron is excited by a pat-
tern belonging to foreground is decreased. Vice versa,
the more seldom a feature vector value corresponding
to a pattern neuron is encountered the more likely it
is that the patterns represented by it belong to fore-
ground objects. By adjusting the learning rates, it is
possible to control the speed of the learning process.
The output of the classification subnet indicates
whether the output of the background summation neu-
ron is higher than that of the foreground summation
neuron, i.e. that it is more probable that the input fea-
ture value is due to a background object rather than a
foreground object based on criterion 5. If the criterion
5 is satisfied than the pixel is classified as background,
otherwise it is classified as foreground.
The activation and replacement subnets are
Winner-Take-All (WTA) neural networks. The acti-
vation subnet performs a dual function: it determines
which of the neurons of the network has the maxi-
mum activation (output) and whether that value ex-
ceeds a threshold (θ) provided as a parameter to the
algorithm. If it does not, the BNN is considered in-
active and replacement of a pattern neuron’s weights
with the values of the current input vector is required.
If this is the case, the feature is considered to belong
to a foreground object.
The first layer of this network has the structure of
a 1LF-MAXNET (Kwan, 1992) network and a single
neuron is used to indicate whether the network is ac-
tive. The output of the neurons of the first layer of the

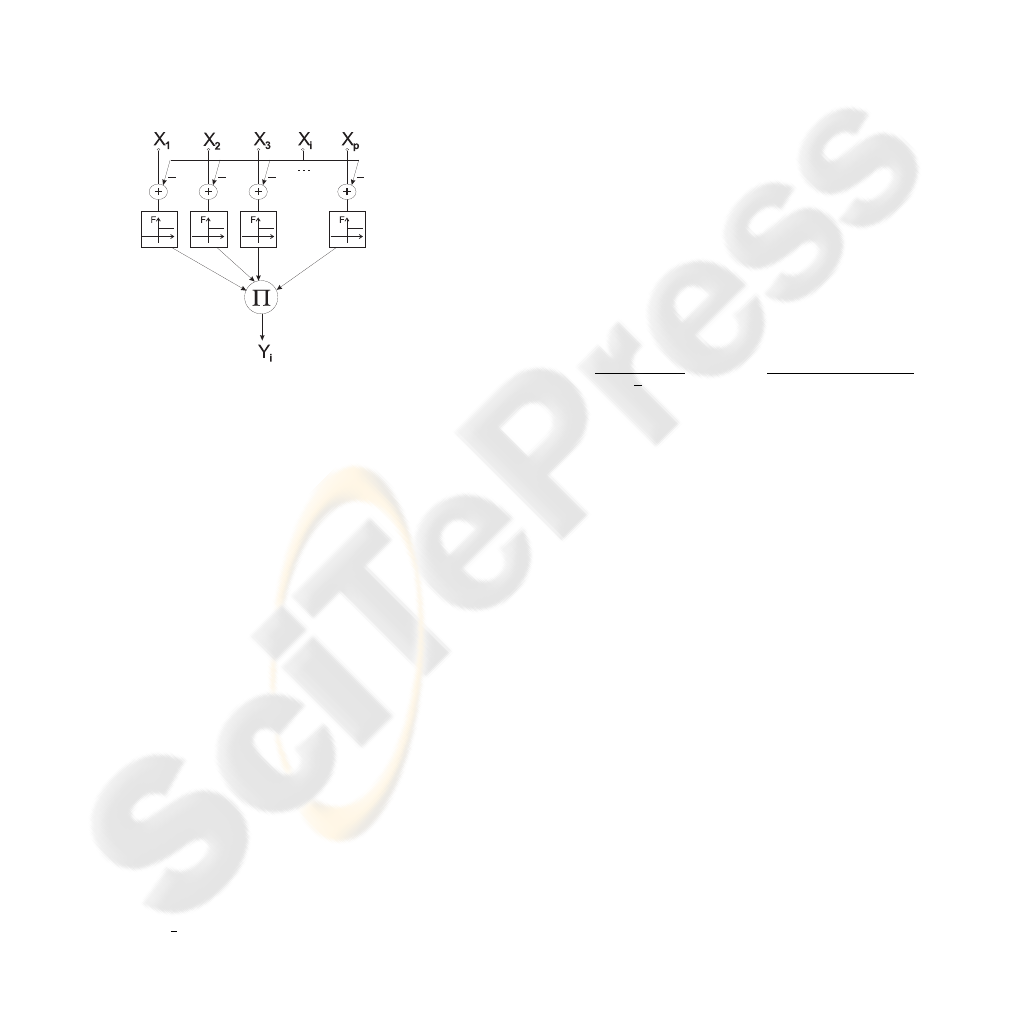
network can be expressed in the form of the following
equation:
Y
j
= X
j
×
P
∏
i=1
{F(X
j
−X
i
|i 6= j)} (11)
where:
F(z) =

1, if z ≥ 0;
0, if z < 0;
(12)
The output of the first layer of the activation subnet
will differ from 0 only for the neurons with maxi-
mum activation and will be equal to the maximum ac-
tivation. In Figure 1 these outputs are indicated with
Z
1
, , Z
P
. Figure 2 shows the inner structure of a neu-
ron in the first layer of the subnet. A single neuron in
Figure 2: Structure of processing neurons of the activation
subnet.
the second layer of the activation subnet is concerned
with detecting whether the BNN is active or not and
its function can be expressed in the form of the fol-
lowing equations:
NA = F(
P
∑
i=1
Z
i
−θ) (13)
where F is given by Equation 12 and θ is the acti-
vation threshold. Finally, the replacement subnet in
Figure 1 can be viewed as a separate neural net with
the unit input. Each of the first-layer neurons in the
replacement subnet is connected with the input via
synapses that have the same weight as the two out-
put synapses between the pattern and summation neu-
rons of the classification subnet. Each pattern neuron
has a corresponding neuron in the replacement net.
The function of the replacement net is to determine
the pattern neuron that minimizes the criterion for re-
placement, expressed by the following equation:
replacement
criterion = w
t
if
+ |w
t
ib
−w
T
if
| (14)
The criterion is a mathematical expression of the idea
that those patterns that are least likely to belong to the
background and those that provide least confidence
to make the decision should be eliminated from the
model.
The neurons of the first layer calculate the negated
value of the replacement criterion for the pattern neu-
ron they correspond to. The second layer is a 1LF-
MAXNET that yields non-zero output corresponding
to the pattern neuron to be replaced.
To form a complete background-subtraction solu-
tion a single instance of a BNN is used to model the
features at each pixel of the image.
4 AUTOMATIC KERNEL WIDTH
ESTIMATION
BNNs employ a Parzen-estimator-based (Parzen,
1962) representation of the PDFs needed to achieve
classification. This class of estimators is nowadays
also known as kernel-based density estimators and
was used in the approach presented in (ElGammal
et al., 2002), as discussed in Section 2. A Parzen esti-
mator of a PDF based on a set of measurements used
within BNNs has the following analytical form:
p(X) =
1
(2π)
P
2
T
o
σ
P
T
o
∑
t=0
exp[−
(X −X
t
)
T
(X −X
t
)
2σ
2
]
(15)
where P is the dimension of the feature vector, T
o
is
the number of patterns used to estimate the PDF (ob-
served pixel values), X
t
are the pixel values observed
up to the frame T
o
, σ is the kernel width.
The Parzen estimator defined by (15) is a sum of
multivariate Gaussian distributions centered at the ob-
served pixel values. As the number of observed values
approaches infinity, the Parzen estimator converges
to its underlying parent density, provided that it is
smooth and continuous. To reduce the memory and
computational requirements of the segmentation, the
BNNs employ a relatively small number of kernels
(up to 30 kernels showed good results in our exper-
iments), but the kernels are used to represent more
than one observation and assigned weights in a man-
ner similar to that discussed in (Specht, 1991). In
addition, due to the format of the classification crite-
rion 5 the normalizing expression preceding the sum
in Equation 15 can be omitted for BNN purposes.
The smoothing parameter (σ) controls the width
of the Gaussians. Fig. 3 shows the plot of a Parzen
estimator for three stored points with values in a sin-
gle dimension (e.g. if only the intensity value for a
pixel is considered).
The horizontal lane in Fig. 3 represent the thresh-
old values used to decide which feature values are

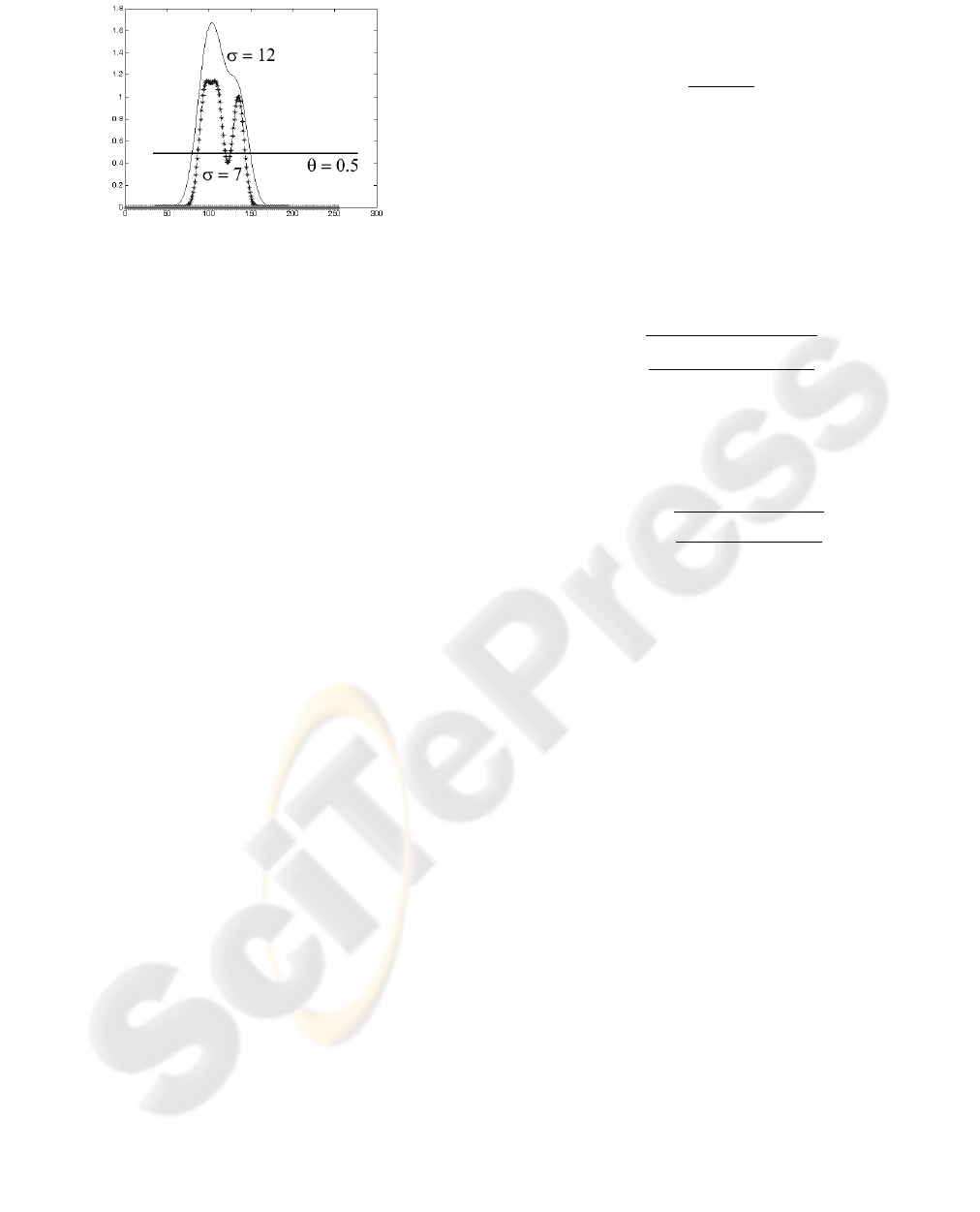
Figure 3: Plots of Parzen estimators for different values of
”smoothing parameter”.
covered by a single Gaussian. The threshold was set
to 0.5 in the plot. All features within the circle defined
by the cross-section of a single Parzen kernel and the
threshold plane are deemed close enough to the cen-
ter of the peak to be within the cluster pertinent to
the Gaussian. The selection of smoothing parameter
value and the threshold controls the size of the cluster.
Larger values of σ lead to less pronounced peaks in
the estimation, i.e. make the estimation ”smoother”.
The value of smoothing parameter has profound
impact on the quality of segmentation and requires
tedious experimentation to determine for a particular
pixel feature used for segmentation. To alleviate this
deficiency of the BNN approach, an automatic pro-
cedure is proposed for learning and adaptation of the
smoothing parameter based on the properties of the
segmented sequence.
The number of kernels in a BNN is fixed, and
determined by the available computational resources.
The smoothing parameter should be selected so that
the predetermined number of kernels is able to cover
all the pixel values occurring due to background. In
addition, a more accurate approximation of PDFs can,
in general, be achieved by the kernel of smaller width.
Thus, the goal of smoothing parameter estimation is
to determine the minimum width of kernels needed to
account for all the background pixel values, based on
a predefined number of kernels and the BNN activa-
tion threshold. To achieve this goal, the kernel width
is updated with each new pixel value observed.
Let σ
i
and µ
i
be estimates of the standard devia-
tion and mean of the background pixel values in the
observed part of the video sequence, along the i-th di-
mension of the pixel feature vector. In order not to
increase the computational and memory requirements
of the BNN, it is desirable to estimate σ
i
and µ
i
based
on the information already contained in the BNN.
For an estimate of the mean µ
i
we use the average
value of the i-th coordinate of patterns stored in the
network, which correspond to the weights between
the i-th input neuron and each pattern neuron of the
classification subnet of BNN :
µ
i
=
∑
P
j=1
w
ij
P
(16)
To estimate the standard deviation σ
i
, the average
of the distance of each center form µ
i
is calculated,
weighted with the weights of the connections between
each pattern neuron and summation neuron corre-
sponding to the background. This way the contribu-
tion of patterns likely to correspond to background is
exacerbated, while the influence of the patterns due to
foreground is diminished. The formula for σ
i
is given
by Equation 17.
σ
i
=
s
∑
P
j=1
w
bi
∗(w
i
j−µ
i
)
2
P−1
(17)
Since the width of the BNN kernels is the same
along each dimension of the feature vector, maximum
standard deviation over all the dimensions is used to
estimate the smoothing parameter:
σ = 0.5∗
s
−2∗max
i∈1..N
dim
σ
i
logθ
(18)
where θ corresponds to the BNN activation threshold.
Equation 18 corresponds to the kernel that will be ac-
tive for all patterns within two estimated maximum
standard deviations. The factor of two is introduced,
since the estimator based on 17 tends to underestimate
the real deviation. Equation 17 would give a precise
estimate based on stored patterns, if all of them corre-
sponded to background and the confidence of of them
pertaining to background was one. It is unlikely that
all the stored patterns in the BNN will correspond to
background. In addition, the confidence that these
patterns corresponds to the background will usually
be less than one.
5 EXPERIMENTS AND RESULTS
To evaluate the approach, a PC-based foreground seg-
mentation application based on the BNN methodol-
ogy and employing adaptive kernels, has been devel-
oped. BNNs containing 30 processing neurons in the
classification subnet were used. Pixel intensity was
used as a feature to guide the segmentation. The ac-
tivation threshold (θ) of the BNNs was set to 0.5, but
the methodology showed itself to be robust to a wide
range of threshold values. The learning rates used
were 0.01, 0.005 and 0.003 depending on the dynam-
ics of the sequence.

(a) (b) (c)
Figure 4: Results obtained for campus sequence: (a) frame from the original sequence, (b) segmentation results obtained for
the frame shown, (c) ground truth frame.
(a) (b) (c)
Figure 5: Results obtained for room sequence: (a) frame from the original sequence, (b) segmentation results obtained for the
frame shown, (c) ground truth frame.
A set of diverse sequences containing complex
background conditions, provided by Li et al. (Li
et al., 2004) and publicly available at
http://
perception.i2r.a-star.edu.sg
, was used. The
results of the segmentation were evaluated both quali-
tatively and quantitatively, using a set of ground truth
frames provided by the same authors for the differ-
ent sequences. The ten testing sequences were ob-
tained in several different environments. They can
be classified based on the sources of complexity in
background variation, pertinent to each environment.
Three classes of sequences (environments) can be
identified: outdoor environments, small indoor envi-
ronments and large (public) indoor environments.
The sources of complexity in the sequences ob-
tained in outdoor environments are usually due to ob-
jects moved by wind (e.g. trees or waves) and illu-
mination changes due to changes in cloud cover. For
small indoor environments, such as offices, the source
of complexity related mostly to objects such as cur-
tains or fans moving in the background or screens
flickering. The illumination changes are mostly due
to switching lights on and off. Large public indoor en-
vironments (e.g. subway stations, airport halls, shop-
ping centers etc.) are characterized by lighting dis-
tributed from the ceiling and presence of specular sur-
faces, inducing complex shadow and glare effects. In
addition, these spaces can contain large moving ob-
jects such as escalators and elevators.
For reasons of space, frames illustrating qualita-
tive results for a single sequence representative of
each class are presented in this paper. More complete
results as well as Matlab scripts that can be used to
evaluate the approach in a manner similar to that de-
scribed in (Culibrk, 2006) and (Li et al., 2004) can be
found at
http://mlab.fau.edu .
The frames shown in Figure 4 are pertinent to
a video of a campus driveway. The complexity of
the background in this sequence is due to the trees
in the background moving violently in the wind and
due to the changing illumination. The Figure shows
the frame of the original sequence, segmentation re-
sult enhanced through morphological processing and
human-generated ground truth. Figure 5 shows a seg-
mentation result achieved for a small indoor environ-
ment sequence. The background is complex due to
the moving curtain. Figure 6 shows a segmentation
result achieved for a large indoor environment of a
shopping mall. The changing glare of the floor makes
the background complex in this case.

(a) (b) (c)
Figure 6: Results obtained for shopping mall sequence: (a) a frame of the original sequence, (b) segmentation result and (c)
ground truth frame.
The results obtained for all three sequences and
indeed all other testing sequences are good, although
the intensity only based segmentation is prone to
shadow segmentation effects as noted in (ElGammal
et al., 2002).
6 CONCLUSION
Object segmentation is a fundamental task in several
important domains of video processing. We proposed
an enhancement of the Background modelling Neural
Network approach to foreground segmentation. Auto-
matic selection of the kernel width for the estimators
used within the methodology, has been introduced.
The proposed kernel width estimation principle en-
ables the BNN to adapt to the conditions of a specific
video, makes the methodology easier to use and al-
lows for easier evaluation of the BNN approach.
The methodology has been tested using a publicly
available and diverse set of sequences and achieves
good segmentation results. Further testing of the
methodology and application of the approach to prob-
lems of segmentation results enhancement and object
tracking represent some of the possible directions of
future research.
REFERENCES
Boult, T., Micheals, R., X.Gao, Lewis, P., Power, C., Yin,
W., and Erkan, A. (1999). Frame-rate omnidirec-
tional surveillance and tracking of camouflaged and
occluded targets. In Proc. of IEEE Workshop on Vi-
sual Surveillance, pp. 48-55.
Culibrk, D. (2006). Neural Network Approach to Bayesian
Background Modeling for Video Object Segmentation.
Ph.D. Dissertation, Florida Atlantic University, USA.
Culibrk, D., Marques, O., Socek, D., Kalva, H., and Furht,
B. (2006). A neural network approach to bayesian
background modeling for video object segmentation.
In Proc. of the International Conference on Computer
Vision Theory and Applications (VISAPP’06).
ElGammal, A., Duraiswami, R., Harwood, D., and Davis,
L. (2002). Background and foreground modeling us-
ing nonparametric kernel density estimation for visual
surveillance. In Proc. of the IEEE, vol. 90, No. 7, pp.
1151-1163.
Ellis, T. and Xu, M. (2001). Object detection and tracking
in an open and dynamic world. In Proc. of the Second
IEEE International Workshop on Performance Evalu-
ation on Tracking and Surveillance (PETS’01).
Karmann, K. P. and von Brandt, A. (1990). Moving ob-
ject recognition using an adaptive background mem-
ory. In Timevarying Image Processing and Moving
Object Recognition, 2, pp. 297-307. Elsevier Publish-
ers B.V.
Kwan, H. K. (1992). One-layer feedforward neural network
fast maximum/minimum determination. In Electron-
ics Letters, pp. 1583-1585.
Li, L., Huang, W., Gu, I., and Tian, Q. (2004). Statistical
modeling of complex backgrounds for foreground ob-
ject detection. In IEEE Trans. Image Processing, vol.
13, pp. 1459-1472.
Mood, A. M. and Graybill, F. A. (1962). Introduction to the
Theory of Statistics. Macmillan.
Parzen, E. (1962). On estimation of a probability density
function and mode. In Ann. Math. Stat., Vol. 33, pp.
1065-1076.
Rosin, L. (1998). Thresholding for change detection. In
Proc. of the Sixth International Conference on Com-
puter Vision (ICCV’98).
Specht, D. F. (1991). A general regression neural network.
In IEEE Trans. Neural Networks, pp. 568-576.
Stauffer, C. and Grimson, W. (2000). Learning patterns of
activity using real-time tracking. In IEEE Trans. Pat-
tern Analysis and Machine Intelligence, vol. 22, pp.
747-757.
Wirth, M., Fraschini, M., Masek, M., and Bruynooghe, M.
(2006). Performance evaluation in image processing.
In EURASIP Journal on Applied Signal Processing,
Vol. 2006, pp. 13.